Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеу 6 сынып

1 слайд
21.01.2019 Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеу

1 слайд

2 слайд
Оқу мақсаттары: 6.2.2.4 түріндегі теңдеулерді шешу, мұндағы a және b – рационал сандар;

2 слайд

3 слайд
Бағалау критерийлері: Оқушылар: - Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеуді шешуде координаталық түзудегі нүктелердің арақашықтығын пайдалана алады; - Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеуді шешуде санның модулінің анықтамасының формуласын пайдалана алады; - Есептеулерде санның модулінің қасиеттерін пайдалана алады; - Бір айнымалысы бар теңдеудің қасиеттерін біледі; - Бір айнымалысы бар сызықтық теңдеулерді шеше біледі.

3 слайд

4 слайд
Психологиялық ахуал Өмірде ойлап тұрсаң, бәріде есеп, Ауырсаң ішетұғын дәріде есеп. Есепсіз өмір деген мазмұнсыз - ау, Дүниенің бар тұлғасы есеп десек.

4 слайд

5 слайд
«Өрмекшінің торы»

5 слайд

6 слайд
Сыныпты топтарға бөлу. 1-топ «Көк кәмпиттер» 2-топ «Қызыл кәмпиттер»

6 слайд

7 слайд
Үй тапсырмасын тексеру

7 слайд

8 слайд
21.01.2019 Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеу

8 слайд

9 слайд
2) Санның модулінің анықтамасының а , егер а ≥ 0 болса, -а , егер а < 0 болса формуласы пайдаланылады. Жаңа сабақ. | x|=3, |x-4|=5, |2x+3|=4, 3|x|-2=7 теңдеулері айнымалысы модуль ішінде берілген бір айнымалысы бар сызықтық теңдеулер. Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеулерді шешуде: 1) Координаталық түзудегі А(а) және В(в) нүктелерінің арақашықтығы пайдаланылады: | a – в |; | a | =

9 слайд

10 слайд
| а | ≥ 0 ; | - а | = | а | ; | а b | = | а | * |b| ;; 0 ,   b b а b а 2 2 а а Модульдің негізгі қасиеттері:

10 слайд

11 слайд
5 3 5 3      3 2 3 2  2 2 7 7  Мысалдар: 1) 2) 3)

11 слайд

12 слайд
Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеуді шешудің екі тәсілін қарастырамыз: 1-тәсіл. | a - b | - –координаталық түзудегі екі нүктенің арақашықтығын пайдаланып шешу. 2-тәсіл. – санның модулінің анықтамасын пайдаланып шешу.

12 слайд

13 слайд
Демек, х = -5 немесе х= 5 2 – тәсілмен. Шешуі: 1) Егер х ≥ 0 болса, 2) Егер х < 0 болса х =5 -х =5 х = - 5 Демек, х = 5 немесе х = - 5 . Жауабы: - 5; 5 1 - мысал: : | х | = 5 теңдеуін шешейік. 1 – тәсілмен. Шешуі: |х - 0| = 5. Координаталық түзу бойындағы О (0) нүктесінен қашықтығы 5 бірлікке тең нүктелерді табу керек. Координаталық түзу бойында О (0) нүктесінен 5 бірлікке тең қашықтықта екі нүкте кескінделеді. Олар координаталары – 5 және 5 нүктелері

13 слайд

14 слайд
2 – мысал. |х - 3| = 4 теңдеуі берілсін. 1 – тәсілмен. Шешуі: |х - 3| = 4 теңдеуінің түбірлері – координаталық түзу бойындағы координатасы 3 – ке тең нүктеден қашықтығы 4 бірлікке тең нүктелердің координаталары. Координаталық түзу бойындағы координатасы 3 нүктесінен координаталары – 1 және 7 нүктелерінің арақашықтығы 4 бірлікке тең Онда – 1 және 7 сандары берілген теңдеудің түбірлері болып табылады, х = - 1 немесе х = 7. 2 – т әсілмен . Шешуі. Егер х – 3 ≥0 болса, 2) Егер х-3 < 0 болса х – 3 = 4, -(х - 3 )= 4, х =7. х -3= -4, х = -1.

14 слайд

15 слайд
№ 823 «Қашықтықты анықтау» тәсілімен теңдеуді шешіңдер (есепті шығарып біткен топ 2 рет шапалақтап, қолдарымен шеңбер құрады) : 1) |а|=8 3)-|c|=-3 5) -|-x|=-10 2) |-b|=9 4)|d|=0 6) -|-y|=-4

15 слайд

16 слайд
№ 824Теңдеуді шешіңдер: 1) | x|+3=5 2)| y|-2=1 3)| 2x|+3=9 4)| 5y|-4=6 5) 3/7+|4x |=1 6) 4+ | 3y|=7

16 слайд

17 слайд
Сергіту сәті «Жасырылған жұмбақтар» Түзудің бір бөлігі, Екі шеткі нүкте көрігі. Ұзындығы және бар, Айтшы ұпай сенікі. Он бір түйе, 5 жылқы, 2 сиыр, 5 ешкі. 2 қоян, 3 түлкі, Таба алмасаң бос күлкі. Темір аяқты, Ағаш таяқты. 

17 слайд

18 слайд
Бар саннан бұрын тұрамын, Өзгерер кейде тұрағым Жоқ өзінде баста, қаста, мойында Ұзындығы жазулы бір бойында   Атадан 10 баламыз Бір - бір жастан арамыз Қосылып кейде басымыз Азайып кейде қаламыз Бөлініп кейде арамыз Көбейіп те аламыз Бірдей санды бірнеше рет Көбейтуден тұрады Егер оны ықшамдасаң Қандай атау болады? Алды артымыз тексіз де, Жете алмайсың біздерге Сәуле менен кесінді Шыққан тегін білсінде   Доп емес, дөңгелек емес, Ұқсас бірақ достарым Тыңда ол ең негізгі Дәл жауапты қостадым

18 слайд

19 слайд
№ 825 Теңдеуді шешіңдер: 1) | x+3|=0 2) | x-5|=0 3) | 1+x|=0

19 слайд

20 слайд
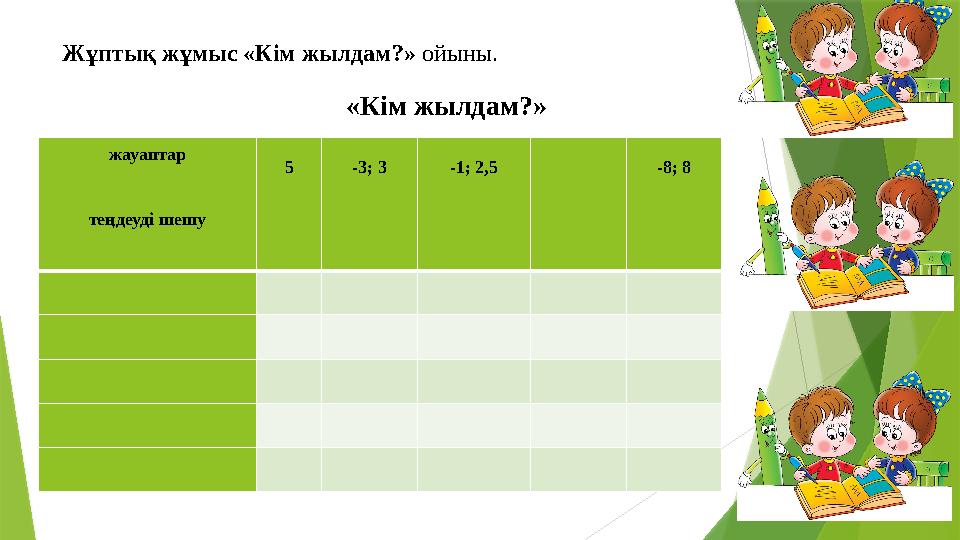
«Кім жылдам?» жауаптар   теңдеуді шешу 5 - 3 ; 3 -1; 2,5 -8; 8                                                  Жұптық жұмыс «Кім жылдам?» ойыны.

20 слайд

21 слайд
Рефлекция. «Бес саусақ» әдісі. Оқушылар сабақтан алған әсерлерін жазып іледі МАТЕМАТИ КА

21 слайд

22 слайд
№ 825 (4,5,6) 22 бет

22 слайд