Ашық сабақ Виет теоремасы 8 сынып
Ашық сабақ Виет теоремасы 8 сынып


#1 слайд
Виет теоремасы
Алгебра 8 сынып
1 слайд
Виет теоремасы Алгебра 8 сынып

#2 слайд
Сабақ мақсаты:
1. Виет теоремасын тұжырымдау және дәлелдеу.
Квадрат теңдеулерді түбірлердің қасиеттерін
қолдану арқылы шешуді үйрету;
2. Оқушыларға Виет теоремасын қолдану
тәсілдерімен таныстыру және квадрат
теңдеулерді шешуді үйрету және оқушылардың
ой-өрісін дамыту.
3. Виет теоремасын қолдана отырып есептер
шығаруға оқушыларды баулу және дағдыландыру.
2 слайд
Сабақ мақсаты: 1. Виет теоремасын тұжырымдау және дәлелдеу. Квадрат теңдеулерді түбірлердің қасиеттерін қолдану арқылы шешуді үйрету; 2. Оқушыларға Виет теоремасын қолдану тәсілдерімен таныстыру және квадрат теңдеулерді шешуді үйрету және оқушылардың ой-өрісін дамыту. 3. Виет теоремасын қолдана отырып есептер шығаруға оқушыларды баулу және дағдыландыру.

#3 слайд
Қайталау сұрақтары:
1. түріндегі теңдеу қалай аталады?
2. формуласымен есептелетін сан қалай аталады?
3. Егер D>0 болса, онда квадрат теңдеудің неше түбірі болады?
4. Егер D=0 болса, онда квадрат теңдеудің неше түбірі болады?
5. Егер D<0 болса, онда квадрат теңдеудің неше түбірі болады?
6. Қандай жағдайда квадрат теңдеу келтірілген квадраттық
теңдеу деп атайды?
7. теңдеуінің коэффициенттерін атап
шығыңдар.
8. Егер квадрат теңдеуінде коэффициенттердің бірі b не с
немесе b мен с-ның екеуі де 0-ге тең болса, мұндай
теңдеулерді қалай атайды?
0
2
cbxах
acb4
2
0352
2
хх
3 слайд
Қайталау сұрақтары: 1. түріндегі теңдеу қалай аталады? 2. формуласымен есептелетін сан қалай аталады? 3. Егер D>0 болса, онда квадрат теңдеудің неше түбірі болады? 4. Егер D=0 болса, онда квадрат теңдеудің неше түбірі болады? 5. Егер D<0 болса, онда квадрат теңдеудің неше түбірі болады? 6. Қандай жағдайда квадрат теңдеу келтірілген квадраттық теңдеу деп атайды? 7. теңдеуінің коэффициенттерін атап шығыңдар. 8. Егер квадрат теңдеуінде коэффициенттердің бірі b не с немесе b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді қалай атайды? 0 2 cbxах acb4 2 0352 2 хх
#4 слайд
2x
2
+3x+1=
0
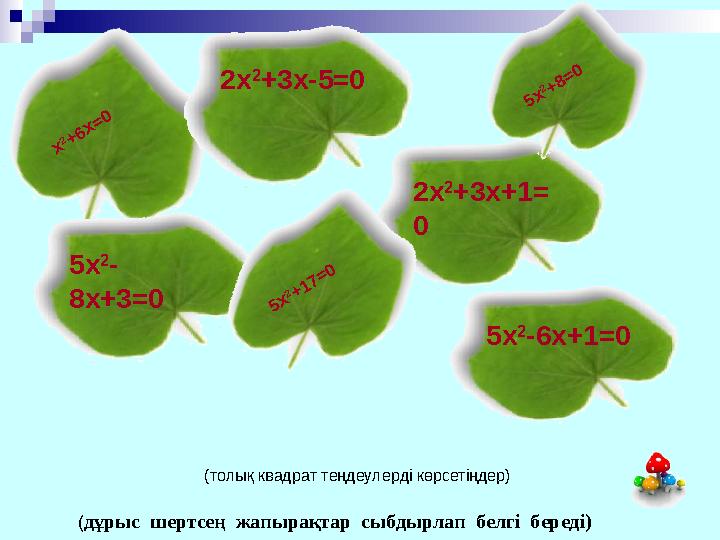
(дұрыс шертсең жапырақтар сыбдырлап белгі береді)
x
2+6x=0
5x
2
-6x+1=0
2x
2
+3x-5=0
5x
2
-
8x+3=0 5x
2+17=0
5x
2+8=0
(толық квадрат теңдеулерді көрсетіңдер)
4 слайд
2x 2 +3x+1= 0 (дұрыс шертсең жапырақтар сыбдырлап белгі береді) x 2+6x=0 5x 2 -6x+1=0 2x 2 +3x-5=0 5x 2 - 8x+3=0 5x 2+17=0 5x 2+8=0 (толық квадрат теңдеулерді көрсетіңдер)

#5 слайд
Түбірлері бар бірнеше келтірілген квадрат
теңдеудің түбірлерін, түбірлерінің қосындысы
мен көбейтіндісінің мәндерін табыңдар және
жауаптарын кестеге толтырыңдар.
Теңдеулер Түбірлер
х
1
және х
2
х
1+ х
2х
1 · х
2
х
2
– 2х – 3 = 0
Х
2
+ 5х – 6 = 0
х
2
– х – 12 = 0
х
2
+ 7х + 12 = 0
х
2
– 8х + 15 = 0
5 слайд
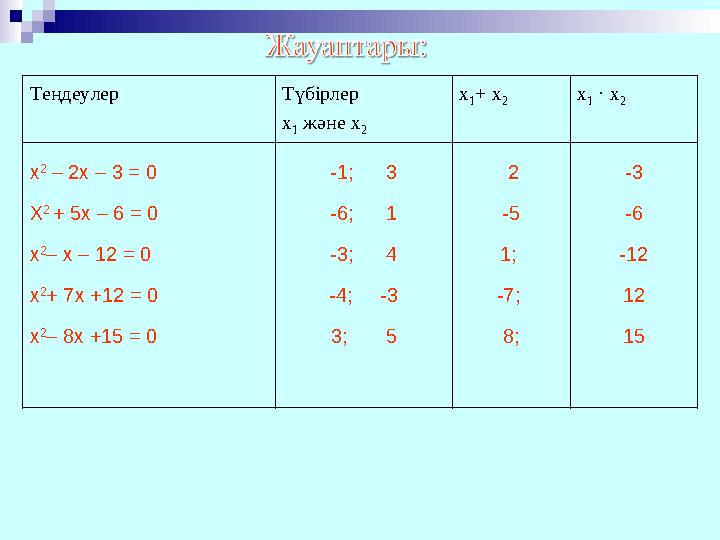
Түбірлері бар бірнеше келтірілген квадрат теңдеудің түбірлерін, түбірлерінің қосындысы мен көбейтіндісінің мәндерін табыңдар және жауаптарын кестеге толтырыңдар. Теңдеулер Түбірлер х 1 және х 2 х 1+ х 2х 1 · х 2 х 2 – 2х – 3 = 0 Х 2 + 5х – 6 = 0 х 2 – х – 12 = 0 х 2 + 7х + 12 = 0 х 2 – 8х + 15 = 0
#6 слайд
Теңдеулер Түбірлер
х
1
және х
2
х
1
+ х
2
х
1
· х
2
х
2
– 2х – 3 = 0
Х
2
+ 5х – 6 = 0
х
2
– х – 12 = 0
х
2
+ 7х +12 = 0
х
2
– 8х +15 = 0
-1; 3
-6; 1
-3; 4
-4; -3
3; 5
2
-5
1;
-7;
8;
-3
-6
-12
12
15
6 слайд
Теңдеулер Түбірлер х 1 және х 2 х 1 + х 2 х 1 · х 2 х 2 – 2х – 3 = 0 Х 2 + 5х – 6 = 0 х 2 – х – 12 = 0 х 2 + 7х +12 = 0 х 2 – 8х +15 = 0 -1; 3 -6; 1 -3; 4 -4; -3 3; 5 2 -5 1; -7; 8; -3 -6 -12 12 15

#7 слайд
Бұл мысалдардан, келтірілген квадрат теңдеу
түбірлерінің қосындысы қарсы таңбасымен алынған
екінші коэффициентке, ал көбейтіндісі бос мүшеге
тең екенін байқадық.
Енді бұл қасиетті теорема ретінде тұжырымдап
шығайық.
Теорема : Келтірілген квадрат теңдеу
түбірлерінің қосындысы қарсы таңбасымен
алынған екінші коэффициентке, ал көбейтіндісі
бос мүшеге тең болады:
qxxpхх
2121 ;
7 слайд
Бұл мысалдардан, келтірілген квадрат теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең екенін байқадық. Енді бұл қасиетті теорема ретінде тұжырымдап шығайық. Теорема : Келтірілген квадрат теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады: qxxpхх 2121 ;

#8 слайд
(келтірілген квадрат теңдеу)
– екінші коэффициент
– бос мүше
Теңдеудің дискриминанті:
Егер D>0, онда теңдеудің екі түбірі бар: және
Түбірлердің қосындысы:
Түбірлердің көбейтіндісі:
. Сонымен,
2
1
Dр
х
2
2
Dр
х
p
pDрDр
хх
2
2
2
21
4
)()(
22
)()(
22
21
DpDрDр
хх
q
qppDp
4
)4(
4
222
0
2
qpxx
p
q
qpD 4
2
pхх
21
qхх
21
8 слайд
(келтірілген квадрат теңдеу) – екінші коэффициент – бос мүше Теңдеудің дискриминанті: Егер D>0, онда теңдеудің екі түбірі бар: және Түбірлердің қосындысы: Түбірлердің көбейтіндісі: . Сонымен, 2 1 Dр х 2 2 Dр х p pDрDр хх 2 2 2 21 4 )()( 22 )()( 22 21 DpDрDр хх q qppDp 4 )4( 4 222 0 2 qpxx p q qpD 4 2 pхх 21 qхх 21

#9 слайд
Бұл теореманы бірінші дәлелдеген француз
математигі Француа Виет (1540-1603)
болғандықтан, соның атымен аталады.
Өзінің алгебралық ойларын Виет “Аналитикалық
шеберлікке кіріспе” шығармасында жазған.Онда
алгебраны математикалық есептеу әдісіне
айналдыруды ұсынған Виет: “Барлық математик “Барлық математик
ғалымдар алгебрада теңдесі жоқ қазына бар екенін ғалымдар алгебрада теңдесі жоқ қазына бар екенін
білген,бірақ қазынаны табуды білмеді.Олардың білген,бірақ қазынаны табуды білмеді.Олардың
неғұрлым күрделі деп тапқан есептері біздің неғұрлым күрделі деп тапқан есептері біздің
шеберлік арқылы оңай шешіледі”, шеберлік арқылы оңай шешіледі”, - деп жазған.
9 слайд
Бұл теореманы бірінші дәлелдеген француз математигі Француа Виет (1540-1603) болғандықтан, соның атымен аталады. Өзінің алгебралық ойларын Виет “Аналитикалық шеберлікке кіріспе” шығармасында жазған.Онда алгебраны математикалық есептеу әдісіне айналдыруды ұсынған Виет: “Барлық математик “Барлық математик ғалымдар алгебрада теңдесі жоқ қазына бар екенін ғалымдар алгебрада теңдесі жоқ қазына бар екенін білген,бірақ қазынаны табуды білмеді.Олардың білген,бірақ қазынаны табуды білмеді.Олардың неғұрлым күрделі деп тапқан есептері біздің неғұрлым күрделі деп тапқан есептері біздің шеберлік арқылы оңай шешіледі”, шеберлік арқылы оңай шешіледі”, - деп жазған.

#10 слайд
10 слайд

#11 слайд
(дұрыс тапсаң шар әуеге қалықтайды!)
А
.
-
5
;
3
Т.5; 7
С.-6; -4
А.-5;7
А.-5; -3
Қ.-2; 5
Н.6;4
З. 2; 5
Қ.2; -5
;0152)2
;0107)1
2
2
хх
хх
;0352)4
;02410)3
2
2
хх
хх
Сергіту сәті
11 слайд
(дұрыс тапсаң шар әуеге қалықтайды!) А . - 5 ; 3 Т.5; 7 С.-6; -4 А.-5;7 А.-5; -3 Қ.-2; 5 Н.6;4 З. 2; 5 Қ.2; -5 ;0152)2 ;0107)1 2 2 хх хх ;0352)4 ;02410)3 2 2 хх хх Сергіту сәті

#12 слайд
Теңдеулер Түбірлерінің
қосындысы
Түбірлерінің
көбейтіндісі
086
2
хх
032
2
хх
056
2
хх
065
2
хх
027
2
хх
030
2
хх
№147
Оқулықпен жұмыс
12 слайд
Теңдеулер Түбірлерінің қосындысы Түбірлерінің көбейтіндісі 086 2 хх 032 2 хх 056 2 хх 065 2 хх 027 2 хх 030 2 хх №147 Оқулықпен жұмыс
#13 слайд
Теңдеулер Түбірлерінің
қосындысы
Түбірлерінің
көбейтіндісі
4+2=6 4*2=8
-3+1=-2 -3*1=-3
1+5=6 1*5=5
3+2=5 3*2=6
3+4=7 3*4=12
-5+6=1 -5*6=-30
086
2
хх
032
2
хх
056
2
хх
065
2
хх
027
2
хх
030
2
хх
№147
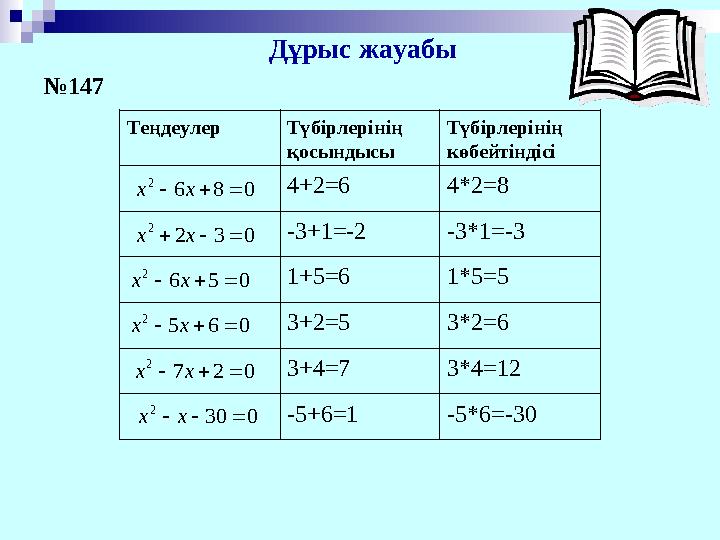
Дұрыс жауабы
13 слайд
Теңдеулер Түбірлерінің қосындысы Түбірлерінің көбейтіндісі 4+2=6 4*2=8 -3+1=-2 -3*1=-3 1+5=6 1*5=5 3+2=5 3*2=6 3+4=7 3*4=12 -5+6=1 -5*6=-30 086 2 хх 032 2 хх 056 2 хх 065 2 хх 027 2 хх 030 2 хх №147 Дұрыс жауабы

#14 слайд
Теңдеулер Түбірлерінің
қосындысы
Түбірлерінің
көбейтіндісі
0643
2
хх
№151
087
2
хх
0152
2
хх
045
2
хх
№150
Теңдеулер Түбірлерінің
қосындысы
Түбірлерінің
көбейтіндісі
02510
2
хх
09124
2
хх
096
2
хх
016249
2
хх
14 слайд
Теңдеулер Түбірлерінің қосындысы Түбірлерінің көбейтіндісі 0643 2 хх №151 087 2 хх 0152 2 хх 045 2 хх №150 Теңдеулер Түбірлерінің қосындысы Түбірлерінің көбейтіндісі 02510 2 хх 09124 2 хх 096 2 хх 016249 2 хх

#15 слайд
1. Теңдеулерді шешіп Виет теоремасы және кері
теорема арқылы тексеріңдер:
а) х
2
- 9х + 8 = 0,
б) х
2
+ 12х + 20 = 0,
в) х
2
- 4х - 21 = 0.
2. х
2
- 12х + с = 0 теңдеуінің бір түбірі х
1=5.
х
1+ х
2=12 және х
1 · х
2=с. с-ны табыңдар.
3. х
2
+рх + 15 = 0 теңдеуінің бір түбірі х
1=3.
х
1+ х
2= -р және х
1 · х
2=15. р-ны табыңдар.
Деңгейлік тапсырмалар
15 слайд
1. Теңдеулерді шешіп Виет теоремасы және кері теорема арқылы тексеріңдер: а) х 2 - 9х + 8 = 0, б) х 2 + 12х + 20 = 0, в) х 2 - 4х - 21 = 0. 2. х 2 - 12х + с = 0 теңдеуінің бір түбірі х 1=5. х 1+ х 2=12 және х 1 · х 2=с. с-ны табыңдар. 3. х 2 +рх + 15 = 0 теңдеуінің бір түбірі х 1=3. х 1+ х 2= -р және х 1 · х 2=15. р-ны табыңдар. Деңгейлік тапсырмалар

#16 слайд
Тест сұрақтары:
1.Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:
А) 8; 15 В) -8; 15 С) 8; -15 D) -8; -15 Е) 5; -18
2. Түбірлері болатын теңдеуді жазыңдар:
А) В) С)
D) Е)
3. теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және
р-ны табыңдар.
А) 2; 5 В) -2; 5 С) -5; -2 D) 2; -5 Е) 5; -1.
4. Теңдеудің түбірлерін табыңдар:
А) 11; 10 В) -1; 10 С) 1; 10 D) 1; -10 Е) -1; -10
5. Келтірілген квадраттық теңдеуді көрсет:
А) В) С)
D) Е)
7,1
21
хх
0158
2
хх
078
2
хх0158
2
хх 078
2
хх
035
2
рхх
078
2
хх078
2
хх
01011
2
хх
0385
2
хх
0152
2
хх 053
2
хх
0158
2
хх 0159
2
хх
16 слайд
Тест сұрақтары: 1.Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар: А) 8; 15 В) -8; 15 С) 8; -15 D) -8; -15 Е) 5; -18 2. Түбірлері болатын теңдеуді жазыңдар: А) В) С) D) Е) 3. теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және р-ны табыңдар. А) 2; 5 В) -2; 5 С) -5; -2 D) 2; -5 Е) 5; -1. 4. Теңдеудің түбірлерін табыңдар: А) 11; 10 В) -1; 10 С) 1; 10 D) 1; -10 Е) -1; -10 5. Келтірілген квадраттық теңдеуді көрсет: А) В) С) D) Е) 7,1 21 хх 0158 2 хх 078 2 хх0158 2 хх 078 2 хх 035 2 рхх 078 2 хх078 2 хх 01011 2 хх 0385 2 хх 0152 2 хх 053 2 хх 0158 2 хх 0159 2 хх

#17 слайд
Дұрыс жауаптары:
1.Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:
А) 8; 15 В) -8; 15 С) 8; -15 D) -8; -15 Е) 5; -18
2. Түбірлері болатын теңдеуді жазыңдар:
А) В) С)
D) Е)
3. теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және
р-ны табыңдар.
А) 2; 5 В) -2; 5 С) -5; -2 D) 2; -5 Е) 5; -1.
4. Теңдеудің түбірлерін табыңдар:
А) 11; 10 В) -1; 10 С) 1; 10 D) 1; -10 Е) -1; -10
5. Келтірілген квадрат теңдеуді көрсет:
А) В) С)
D) Е)
7,1
21
хх
0158
2
хх
078
2
хх0158
2
хх 078
2
хх
035
2
рхх
078
2
хх078
2
хх
01011
2
хх
0385
2
хх
0152
2
хх 053
2
хх
0158
2
хх 0159
2
хх
17 слайд
Дұрыс жауаптары: 1.Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар: А) 8; 15 В) -8; 15 С) 8; -15 D) -8; -15 Е) 5; -18 2. Түбірлері болатын теңдеуді жазыңдар: А) В) С) D) Е) 3. теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және р-ны табыңдар. А) 2; 5 В) -2; 5 С) -5; -2 D) 2; -5 Е) 5; -1. 4. Теңдеудің түбірлерін табыңдар: А) 11; 10 В) -1; 10 С) 1; 10 D) 1; -10 Е) -1; -10 5. Келтірілген квадрат теңдеуді көрсет: А) В) С) D) Е) 7,1 21 хх 0158 2 хх 078 2 хх0158 2 хх 078 2 хх 035 2 рхх 078 2 хх078 2 хх 01011 2 хх 0385 2 хх 0152 2 хх 053 2 хх 0158 2 хх 0159 2 хх

#18 слайд
Сөзжұмбақты шешу.
в
и
е
т
•ах
2
+вх+с=0 (а≠0) теңдеуі қалай аталады?
•Квадрат теңдеудің түбірлерінің формуласындағы түбір
астындағы өрнек
•Квадрат теңдеудегі а және в қалай аталады?
•Квадрат теңдеудің дербес түрі
18 слайд
Сөзжұмбақты шешу. в и е т •ах 2 +вх+с=0 (а≠0) теңдеуі қалай аталады? •Квадрат теңдеудің түбірлерінің формуласындағы түбір астындағы өрнек •Квадрат теңдеудегі а және в қалай аталады? •Квадрат теңдеудің дербес түрі

#19 слайд
Теңдеулердің түбірлерінің
қосындысы мен көбейтіндісін табыңдар:
1) Х ² + х – 2 = 0
2) Х ² +х – 20 = 0
3) X² + х – 6 = 0
4) Х² + х – 42 =0
5) Х ² +3х –18 = 0
6) Х ² + 2х – 48=0
7) Х ² +х – 12 = 0
8) Х ² + 3х – 4=0
1)-3; 2
2)-7; 6
3) -8;6
4)-1;2
5) -5;4
6) -4;3
7) -6;3
8) -4;1
“Жорға” ойыны
19 слайд
Теңдеулердің түбірлерінің қосындысы мен көбейтіндісін табыңдар: 1) Х ² + х – 2 = 0 2) Х ² +х – 20 = 0 3) X² + х – 6 = 0 4) Х² + х – 42 =0 5) Х ² +3х –18 = 0 6) Х ² + 2х – 48=0 7) Х ² +х – 12 = 0 8) Х ² + 3х – 4=0 1)-3; 2 2)-7; 6 3) -8;6 4)-1;2 5) -5;4 6) -4;3 7) -6;3 8) -4;1 “Жорға” ойыны

#20 слайд
Теңдеулердің түбірлерінің
қосындысы мен көбейтіндісін табыңдар:
1) Х ² + х – 2 = 0
2) Х ² +х – 20 = 0
3) X² + х – 6 = 0
4) Х² + х – 42 =0
5) Х ² +3х –18 = 0
6) Х ² + 2х – 48=0
7) Х ² +х – 12 = 0
8) Х ² + 3х – 4=0
1)-3; 2
2)-7; 6
3) -8;6
4)-1;2
5) -5;4
6) -4;3
7) -6;3
8) -4;1
Дұрыс жауабы
20 слайд
Теңдеулердің түбірлерінің қосындысы мен көбейтіндісін табыңдар: 1) Х ² + х – 2 = 0 2) Х ² +х – 20 = 0 3) X² + х – 6 = 0 4) Х² + х – 42 =0 5) Х ² +3х –18 = 0 6) Х ² + 2х – 48=0 7) Х ² +х – 12 = 0 8) Х ² + 3х – 4=0 1)-3; 2 2)-7; 6 3) -8;6 4)-1;2 5) -5;4 6) -4;3 7) -6;3 8) -4;1 Дұрыс жауабы
#21 слайд
1. түріндегі теңдеу
2.
3.
4.
1. түріндегі теңдеу
2.
3.
4.
квадрат теңдеу
деп аталады
квадрат теңдеу
деп аталады
Квадрат теңдеу түбірлерінің
формуласы
Квадрат теңдеу түбірлерінің
формуласы
Келтірілген квадрат теңдеуКелтірілген квадрат теңдеу
Виет теоремасыВиет теоремасы
0
2
cbxax
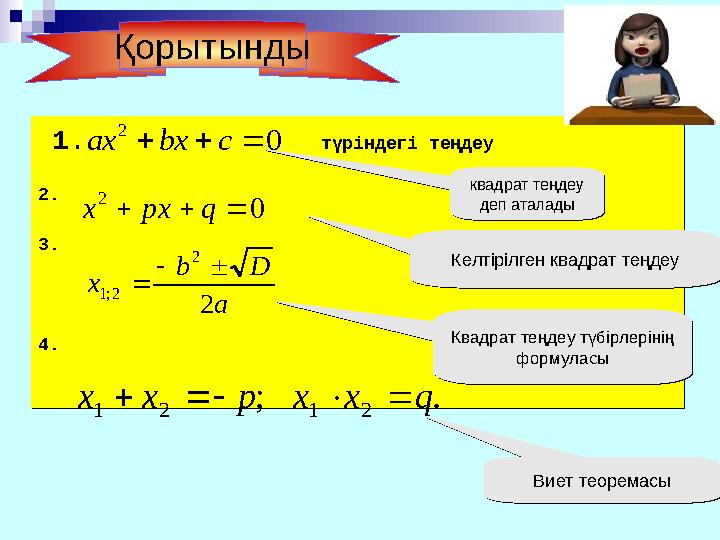
Қорытынды
0
2
qpxx
a
Db
x
2
2
2;1
;
21 pxx .
21 qxx
21 слайд
1. түріндегі теңдеу 2. 3. 4. 1. түріндегі теңдеу 2. 3. 4. квадрат теңдеу деп аталады квадрат теңдеу деп аталады Квадрат теңдеу түбірлерінің формуласы Квадрат теңдеу түбірлерінің формуласы Келтірілген квадрат теңдеуКелтірілген квадрат теңдеу Виет теоремасыВиет теоремасы 0 2 cbxax Қорытынды 0 2 qpxx a Db x 2 2 2;1 ; 21 pxx . 21 qxx

#22 слайд
Үйге тапсырма: §3.
№259, №260 79 бет
Шығу
22 слайд
Үйге тапсырма: §3. №259, №260 79 бет Шығу
#23 слайд
23 слайд

#24 слайд
0
2
cbxах
түріндегі теңдеу
квадрат теңдеу деп
аталады.
24 слайд
0 2 cbxах түріндегі теңдеу квадрат теңдеу деп аталады.

#25 слайд
формуласымен
есептелетін сан
дискриминант деп
аталады.
acb4
2
25 слайд
формуласымен есептелетін сан дискриминант деп аталады. acb4 2

#26 слайд
Егер D>0 болса,
онда квадрат
теңдеудің екі түбірі
болады.
26 слайд
Егер D>0 болса, онда квадрат теңдеудің екі түбірі болады.

#27 слайд
Егер D=0 болса,
онда квадрат
теңдеудің бір
түбірі болады.
27 слайд
Егер D=0 болса, онда квадрат теңдеудің бір түбірі болады.

#28 слайд
Егер D<0 болса,
онда квадрат
теңдеудің түбірі
болмайды.
28 слайд
Егер D<0 болса, онда квадрат теңдеудің түбірі болмайды.

#29 слайд
Егер квадрат теңдеуде
бірінші коэффициент 1-
ге тең болса, онда ол
квадрат теңдеу
келтірілген квадрат
теңдеу деп аталады.
29 слайд
Егер квадрат теңдеуде бірінші коэффициент 1- ге тең болса, онда ол квадрат теңдеу келтірілген квадрат теңдеу деп аталады.

#30 слайд
0352
2
хх
3,5,2 cbа
Бірінші коэффициент 2-ге тең,
екініші коэффициент (-5)-ке тең,
ал үшінші коэффициент (-3)-ке
тең.
30 слайд
0352 2 хх 3,5,2 cbа Бірінші коэффициент 2-ге тең, екініші коэффициент (-5)-ке тең, ал үшінші коэффициент (-3)-ке тең.

#31 слайд
Егер квадрат теңдеуінде
коэффициенттердің бірі b не
с немесе b мен с-ның екеуі де
0-ге тең болса, онда мұндай
теңдеулер толымсыз
квадрат теңдеу.
31 слайд
Егер квадрат теңдеуінде коэффициенттердің бірі b не с немесе b мен с-ның екеуі де 0-ге тең болса, онда мұндай теңдеулер толымсыз квадрат теңдеу.

#32 слайд
Теорема : Келтірілген квадрат
теңдеу түбірлерінің қосындысы
қарсы таңбасымен алынған екінші
коэффициентке, ал көбейтіндісі
бос мүшеге тең болады:
qxx
pхх
21
21
;
32 слайд
Теорема : Келтірілген квадрат теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады: qxx pхх 21 21 ;

шағым қалдыра аласыз
















