Электрсыйымдылық

1 слайд
Capacitance

1 слайд

2 слайд
October 10, 2007What is Capacitance?  From the word “capacity,” it describes how much charge an arrangement of conductors can hold for a given voltage applied. + _ 1.5 V battery+ charges + charges electrons electrons Charges will flow until the right conductor’s potential is the same as the + side of the battery, and the left conductor’s potential is the same as the – side of the battery. V=1.5 V +_  How much charge is needed to produce an electric field whose potential difference is 1.5 V?  Depends on capacitance: CV q  “ Charging” the capacitor definition of capacitance

2 слайд

3 слайд
October 10, 2007What is Capacitance?  From the word “capacity,” it describes how much charge an arrangement of conductors can hold for a given voltage applied. + _ 1.5 V battery+ charges + charges electrons electrons Charges will flow until the right conductor’s potential is the same as the + side of the battery, and the left conductor’s potential is the same as the – side of the battery. V=1.5 V +_  How much charge is needed to produce an electric field whose potential difference is 1.5 V?  Depends on capacitance: CV q  “ Charging” the capacitor definition of capacitance

3 слайд

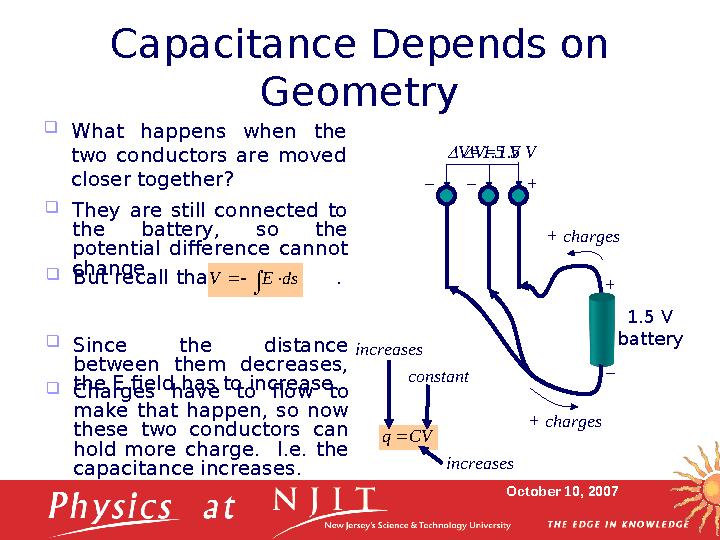
4 слайд
October 10, 2007Capacitance Depends on Geometry  What happens when the two conductors are moved closer together? + _ 1.5 V battery+ charges + charges They are still connected to the battery, so the potential difference cannot change. V=1.5 V +_ CV q   V=1.5 V +_  But recall that .  Since the distance between them decreases, the E field has to increase.     sd E V    Charges have to flow to make that happen, so now these two conductors can hold more charge. I.e. the capacitance increases. constantincreases increases

4 слайд

5 слайд
October 10, 2007Capacitance Depends on Geometry  What happens if we replace the small conducting spheres with large conducting plates?  The plates can hold a lot more charge, so the capacitance goes way up. + _ 1.5 V battery+ charges + charges Here is a capacitor that you can use in an electronic circuit.  We will discuss several ways in which capacitors are useful.  But first, let’s look in more detail at what capacitance is. V=1.5 V +_ Circular plates

5 слайд

6 слайд
October 10, 2007Charge Without Battery 1. Say that we charge a parallel plate capacitor to 20 V, then disconnect the battery. What happens to the charge and voltage? A. The charge stays on the plates indefinitely, and the voltage stays constant at 20 V. B. The charge leaks out the bottom quickly, and the voltage goes to 0 V. C. The charge jumps quickly across the air gap, and the voltage goes to 0 V. D. The charge stays on the plates, but the voltage drops to 0 V. E. The charge instantly disappears, but the voltage stays constant at 20 V.

6 слайд

7 слайд
October 10, 2007Capacitance for Parallel Plates  Parallel plates make a great example for calculating capacitance, because  The E field is constant, so easy to calculate.  The geometry is simple, only the area and plate separation are important.  To calculate capacitance, we first need to determine the E field between the plates. We use Gauss’ Law, with one end of our gaussian surface closed inside one plate, and the other closed in the region between the plates (neglect fringing at ends): Total charge q on inside of plate E and dA parallelq Ad E      0 EA q 0  so  Need to find potential difference  Since E=constant , we have , so the capacitance is         sd E V V V   Ed V  d A Ed EA V q C 0 0 /      V V area A separation d line of integration

7 слайд

8 слайд
October 10, 2007Capacitance for Other Configurations (Cylindrical)  Cylindrical capacitor  The E field falls off as 1/ r .  The geometry is fairly simple, but the V integration is slightly more difficult.  To calculate capacitance, we first need to determine the E field between the plates. We use Gauss’ Law, with a cylindrical gaussian surface closed in the region between the plates (neglect fringing at ends):q Ad E      0  Need to find potential difference  Since E~1/r , we have , so the capacitance is         sd E V V V            a b a b L q r dr L q V ln 2 2 0 0   ) / ln( 2 / 0 a b L V q C    So or ) 2( 0 0 rL E EA q      ) 2 /( 0rL q E  

8 слайд

9 слайд
October 10, 2007Capacitance for Other Configurations (Spherical)  Spherical capacitor  The E field falls off as 1/ r 2 .  The geometry is fairly simple, and the V integration is similar to the cylindrical case.  To calculate capacitance, we first need to determine the E field between the spheres. We use Gauss’ Law, with a spherical gaussian surface closed in the region between the spheres:q Ad E      0  Need to find potential difference  Since E~1/r 2 , we have , so the capacitance is         sd E V V V             a b b a q r dr q V 1 1 4 4 0 2 0   a b ab V q C    0 4 /  So or ) 4( 2 0 0 r E EA q      ) 4 /( 2 0r q E  

9 слайд

10 слайд
October 10, 2007Capacitance Summary  Parallel Plate Capacitor  Cylindrical (nested cylinder) Capacitor  Spherical (nested sphere) Capacitor  Capacitance for isolated Sphere  Units:    length = C 2 /Nm = F (farad), named after Michael Faraday. [note:   = 8.85 pF/m]d A C 0   ) / ln( 2 0 a b L C   a b ab C   0 4  R C 0 4  

10 слайд

11 слайд
October 10, 2007Units of Capacitance 2. Given these expressions, and  0 = 8.85 x 10  12 C 2 /N∙m 2 , what are the units of capacitance? A. The units are different in the different expressions. B. The units are C 2 /N∙m 2 . C. The units are C 2 /N∙m . D. The units are C 2 /N . E. The units are C/V .d A C 0  ) / ln( 2 0 a b L C   a b ab C   0 4 R C 0 4   Units:    length = C 2 /N ∙ m = F (farad) , named after Michael Faraday. [note:   = 8.85 pF/m ]

11 слайд

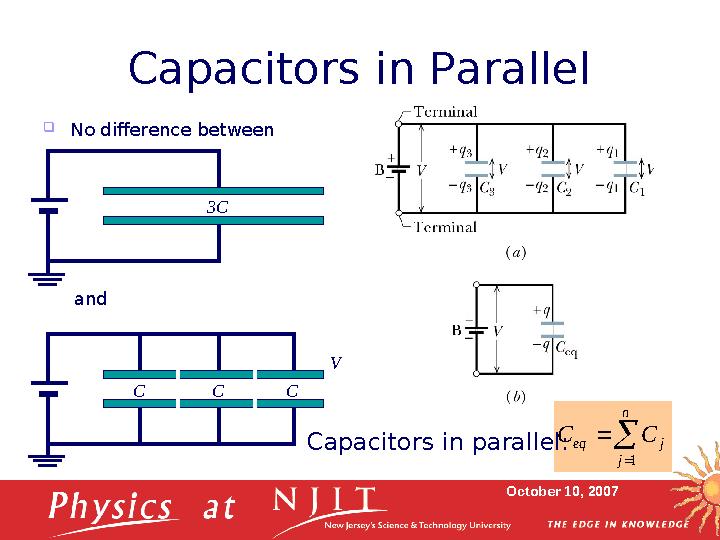
12 слайд
October 10, 2007Capacitors in Parallel  No difference between C C Cand V3C   n j j eq C C 1 Capacitors in parallel:

12 слайд

13 слайд
October 10, 2007Capacitors in Series  There is a difference between   n j j eq C C 1 1 1 Capacitors in series:3C  Charge on lower plate of one and upper plate of next are equal and opposite. (show by gaussian surface around the two plates).  Total charge is q , but voltage on each is only V/3 . C C Cand

13 слайд

14 слайд
October 10, 2007Capacitors in Series  To see the series formula, consider the individual voltages across each capacitor  The sum of these voltages is the total voltage of the battery, V  Since V/q = 1 /C eq , we have3 3 2 2 1 1 , , C q V C q V C q V    3 2 1 3 2 1 C q C q C q V V V V       3 2 1 1 1 1 1 C C C C q V eq    

14 слайд

15 слайд
October 10, 2007Three Capacitors in Series 3. The equivalent capacitance for two capacitors in series is . What is the equivalent capacitance for three capacitors in series? A. B. C. 2 1 2 1 1 1 2 1 1 C C C C C C C eq     3 2 1 3 2 1 C C C C C C C eq    3 2 1 3 1 3 2 2 1 C C C C C C C C C C eq      1 3 3 2 2 1 3 2 1 C C C C C C C C C C eq    D. E. 3 2 1 1 3 3 2 2 1 C C C C C C C C C C eq    3 2 1 3 2 1 C C C C C C C eq   

15 слайд

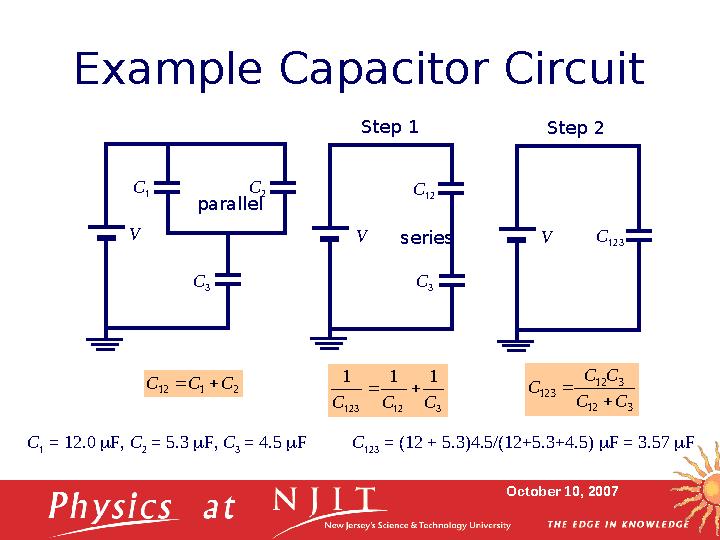
16 слайд
October 10, 2007Example Capacitor Circuit C 3C 1 C 22 1 12 C C C   3 12 123 1 1 1 C C C   3 12 3 12 123 C C C C C   V C 3C 12Step 1 V C 123Step 2 Vparallel series C 1 = 12.0  F, C 2 = 5.3  F, C 3 = 4.5  F C 123 = (12 + 5.3)4.5/(12+5.3+4.5)  F = 3.57  F

16 слайд

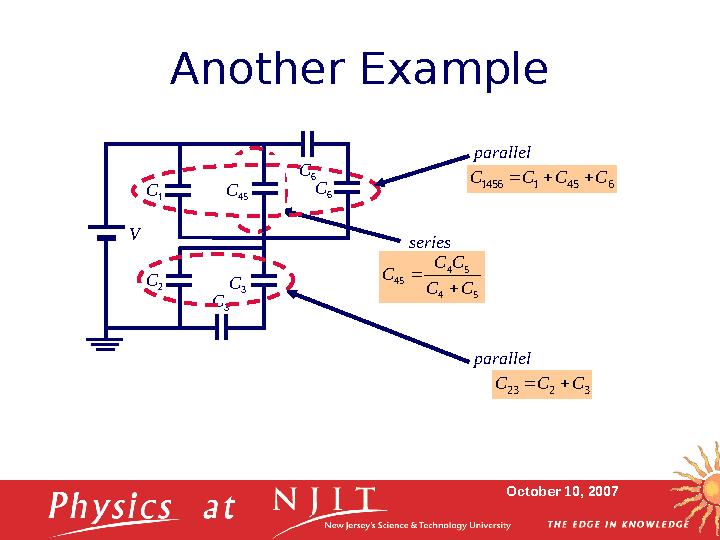
17 слайд
October 10, 2007Another Example C 3C 1 C 2V C 3 C 4 C 5 C 6 C 3 C 6 series5 4 5 4 45 C C C C C  C 45 parallel 6 45 1 1456 C C C C    parallel 3 2 23 C C C  

17 слайд

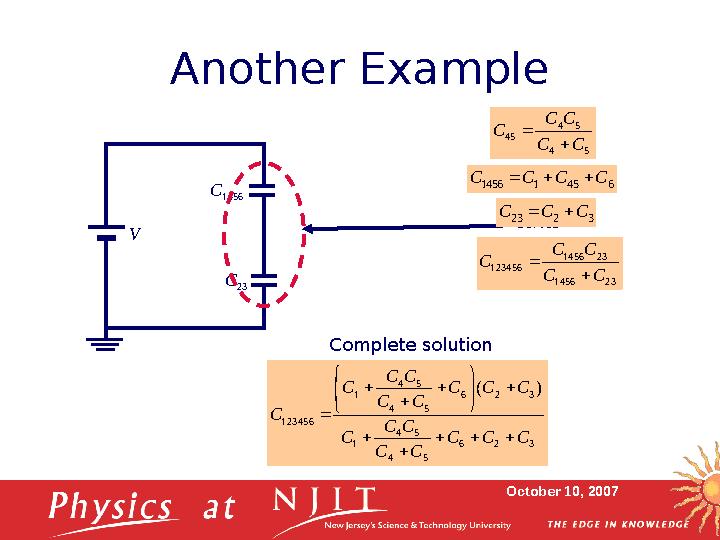
18 слайд
October 10, 2007Another Example C 1456 C 23V series23 1456 23 1456 123456 C C C C C   5 4 5 4 45 C C C C C   6 45 1 1456 C C C C    3 2 23 C C C   23 1456 23 1456 123456 C C C C C   Complete solution 3 2 6 5 4 5 4 1 3 2 6 5 4 5 4 1 123456 ) ( C C C C C C C C C C C C C C C C C                

18 слайд

19 слайд
October 10, 2007Series or Parallel 4. In the circuits below, which ones show capacitors 1 and 2 in series? A. I, II, III B. I, III C. II, IV D. III, IV E. None VC 1 C 3 C 2 V C 2 C 1C 3 V C 3C 1 C 2V C 1 C 2 C 3I II III IV

19 слайд

20 слайд
October 10, 2007Capacitors Store Energy  When charges flow from the battery, energy stored in the battery is lost. Where does it go?  We learned last time that an arrangement of charge is associated with potential energy. One way to look at it is that the charge arrangement stores the energy.  Recall the definition of electric potential V = U/q  For a distribution of charge on a capacitor, a small element dq will store potential energy dU = V dq  Thus, the energy stored by charging a capacitor from charge 0 to q is + _ 1.5 V battery+ charges + chargesV=1.5 V +_ 2 2 1 2 0 2 1 CV C q qd q C U q      Movie 1 Movie 2

20 слайд

21 слайд
October 10, 2007     Ed sd E V  Capacitors Store Energy  Another way to think about the stored energy is to consider it to be stored in the electric field itself.  The total energy in a parallel plate capacitor is  The volume of space filled by the electric field in the capacitor is vol = Ad , so the energy density is  But for a parallel plate capacitor, so 2 0 2 2 1 2 V d A CV U    2 0 2 1 2 0 2          d V V dAd A vol U u   2 0 2 1 E u   Energy stored in electric field

21 слайд

22 слайд
October 10, 2007What Changes? 5. A parallel plate capacitor is connected to a battery of voltage V. If the plate separation is decreased, which of the following increase? A. II, III and IV. B. I, IV, V and VI. C. I, II and III. D. All except II. E. All increase . I. Capacitance of capacitor II. Voltage across capacitor III. Charge on capacitor IV. Energy stored on capacitor V. Electric field magnitude between plates VI. Energy density of E fieldCV q  d A C 0  2 2 1CV U  2 0 2 1 E u  

22 слайд

23 слайд
October 10, 2007 You may have wondered why we write  0 (permittivity of free space), with a little zero subscript. It turns out that other materials (water, paper, plastic, even air) have different permittivities  =  0 . The  is called the dielectric constant , and is a unitless number. For air,  = 1.00054 (so  for air is for our purposes the same as for “free space.”)  In all of our equations where you see  0 , you can substitute  0 when considering some other materials (called dielectrics).  The nice thing about this is that we can increase the capacitance of a parallel plate capacitor by filling the space with a dielectric: Dielectrics Material Dielectri c Constan t  Dielectri c Strength (kV/mm) Air 1.00054 3 Polystyrene 2.6 24 Paper 3.5 16 Transformer Oil 4.5 Pyrex 4.7 14 Ruby Mica 5.4 Porcelain 6.5 Silicon 12 Germanium 16 Ethanol 25 Water (20 º C) 80.4 Water (50 º C) 78.5 Titania Ceramic 130 Strontium Titanate 310 8 C d A C     0

23 слайд

24 слайд
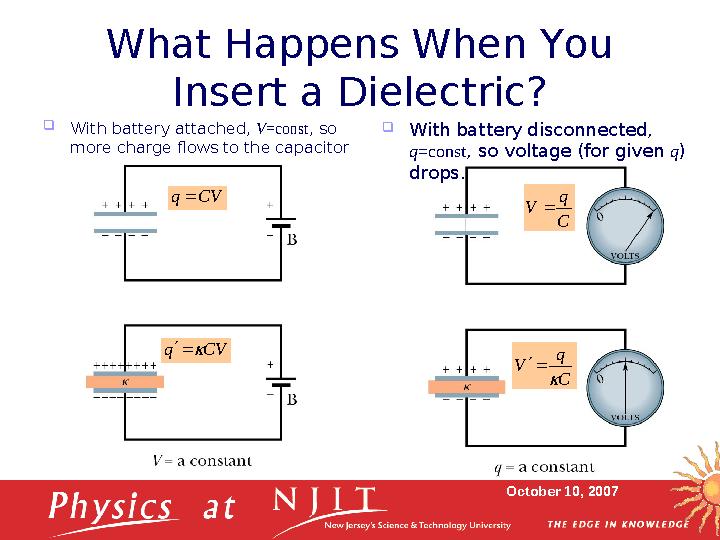
October 10, 2007What Happens When You Insert a Dielectric?  With battery attached, V =const , so more charge flows to the capacitor  With battery disconnected, q =const , so voltage (for given q ) drops.CV q  CV q   C q V  C q V  

24 слайд

25 слайд
October 10, 2007What Does the Dielectric Do?  A dielectric material is made of molecules.  Polar dielectrics already have a dipole moment (like the water molecule).  Non-polar dielectrics are not naturally polar, but actually stretch in an electric field, to become polar.  The molecules of the dielectric align with the applied electric field in a manner to oppose the electric field.  This reduces the electric field, so that the net electric field is less than it was for a given charge on the plates.  This lowers the potential (case b of the previous slide).  If the plates are attached to a battery (case a of the previous slide), more charge has to flow onto the plates.

25 слайд

26 слайд
October 10, 2007What Changes? 6. Two identical parallel plate capacitors are connected in series to a battery as shown below. If a dielectric is inserted in the lower capacitor, which of the following increase for that capacitor? A. I and III. B. I, II and IV. C. I, II and III. D. All except II. E. All increase . I. Capacitance of capacitor II. Voltage across capacitor III. Charge on capacitor IV. Energy stored on capacitorCV q  d A C 0   2 2 1 2 2 CV C q U   V CC 

26 слайд

27 слайд
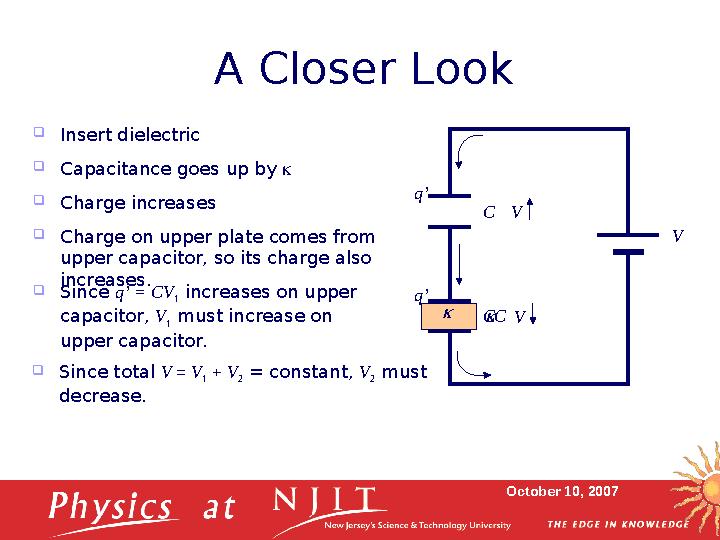
October 10, 2007A Closer Look V CC Insert dielectric  Cq q q’q’ V V Capacitance goes up by   Charge increases  Charge on upper plate comes from upper capacitor, so its charge also increases.  Since q’ = CV 1 increases on upper capacitor, V 1 must increase on upper capacitor.  Since total V = V 1 + V 2 = constant, V 2 must decrease.

27 слайд

28 слайд
October 10, 2007Dielectrics and Gauss’ Law  Gauss’ Law holds without modification, but notice that the charge enclosed by our gaussian surface is less, because it includes the induced charge q’ on the dielectric.  For a given charge q on the plate, the charge enclosed is q – q’ , which means that the electric field must be smaller. The effect is to weaken the field.  When attached to a battery, of course, more charge will flow onto the plates until the electric field is again E 0 .

28 слайд

29 слайд
October 10, 2007Summary  Capacitance says how much charge is on an arrangement of conductors for a given potential.  Capacitance depends only on geometry  Parallel Plate Capacitor  Cylindrical Capacitor  Spherical Capacitor  Isolated Sphere  Units, F (farad) = C 2 /Nm or C/V (note  0 = 8.85 pF/m)  Capacitors in parallel in series  Energy and energy density stored by capacitor  Dielectric constant increases capacitance due to induced, opposing field.  is a unitless number.CV q  d A C 0  ) / ln( 2 0 a b L C   a b ab C   0 4 R C 0 4     n j j eq C C 1    n j j eq C C 1 1 1 2 2 1CV U  2 0 2 1 E u   C C  

29 слайд