Материалдар / Функцияның қасиеттері

Функцияның қасиеттері

Материал туралы қысқаша түсінік

Функцияның қасиеттері тақырыбына жасалған презентация болып табылады.

Қаниев Нұрсұлтан Сабырұлы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

03 Қараша 2018

2456

0 рет жүктелген

Математика Презентация 10 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 13

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Сабақтың тақырыбы: Функцияның қасиеттері

1 слайд

Сабақтың тақырыбы: Функцияның қасиеттері

2 слайд
• Сабақтың міндеттері: Білімділік: Оқушыларды функцияның аталған негізгі қасиеттерімен таныстыру, оларды әртүрлі функцияларды осы қасиеттері бойынша зерттеуге үйрету және кері функция ұғымын беру. Дамытушылық: Оқушылардың математика пәніне деген қызығушылығын арттыру, алған білімдерін қолдана білуге дағдыландыру. Тәрбиелік: Өз жетістігін бағалай білуге, өз бетінше жұмыс жасауға, іздене білуге тәрбиелеу

2 слайд

• Сабақтың міндеттері: Білімділік: Оқушыларды функцияның аталған негізгі қасиеттерімен таныстыру, оларды әртүрлі функцияларды осы қасиеттері бойынша зерттеуге үйрету және кері функция ұғымын беру. Дамытушылық: Оқушылардың математика пәніне деген қызығушылығын арттыру, алған білімдерін қолдана білуге дағдыландыру. Тәрбиелік: Өз жетістігін бағалай білуге, өз бетінше жұмыс жасауға, іздене білуге тәрбиелеу

3 слайд

4 слайд
Сабақтың барысы • Ұйымдастыру кезеңі • Үй жұмысын тексеру • Өткен сабақты бекіту • Жаңа сабақ түсіндіру • Есеп шығару • Қорытындылау • Бағалау Ответы:

4 слайд

Сабақтың барысы • Ұйымдастыру кезеңі • Үй жұмысын тексеру • Өткен сабақты бекіту • Жаңа сабақ түсіндіру • Есеп шығару • Қорытындылау • Бағалау Ответы:

5 слайд
Анықтама • Анықталу облысының кез келген нүктесіндегі f(х) функцияның мәндерінің абсолют шамасы белгілі бір b>0 санынан кіші немесе оған тең болса, яғни |f(x)|≤b, x X, онда ол осы жиында шектелген функция деп аталады. • Мысалы: y=sinx, y=cosx функцияларының мәндерінің абсолют шамалары 1 санынан аспайды. 

5 слайд

Анықтама • Анықталу облысының кез келген нүктесіндегі f(х) функцияның мәндерінің абсолют шамасы белгілі бір b>0 санынан кіші немесе оған тең болса, яғни |f(x)|≤b, x X, онда ол осы жиында шектелген функция деп аталады. • Мысалы: y=sinx, y=cosx функцияларының мәндерінің абсолют шамалары 1 санынан аспайды. 

6 слайд
• Анықталу облысының қайсыбір аралықтарында функция тек оң мәндерді (оның графигі Ох осінің жоғарғы жағында орналасқан), ал басқа аралықтарында тек теріс мәндерді (график Ох осінің төменгі жағында орналасқан) қабылдаса, онда мұндай аралықтарды функция таңбасының тұрақтылық аралықтары деп атайды. Анықтама

6 слайд

• Анықталу облысының қайсыбір аралықтарында функция тек оң мәндерді (оның графигі Ох осінің жоғарғы жағында орналасқан), ал басқа аралықтарында тек теріс мәндерді (график Ох осінің төменгі жағында орналасқан) қабылдаса, онда мұндай аралықтарды функция таңбасының тұрақтылық аралықтары деп атайды. Анықтама

7 слайд
• Егер у = f(х) функциясының анықталу облысындағы кез келген сандары үшін теңсіздігі орындалса, онда функция өспелі , ал теңсіздігі орындалса, онда ол кемімелі деп аталады • Егер у = f(х) функциясының анықталу облысындағы кез келген сандары үшін теңсіздігі орындалса, онда функция кемімейтін , ал теңсіздігі орындалса, онда ол өспейтін функция деп аталады. Өспелі, кемімелі, кемімейтін, өспейтін функцияларды бірсарынды(монотонды) функциялар деп атайды. • а нүктесінің аймағы деп осы нүктені қамтитын кез келген аралықта айтады. Анықтама2 1 x x  ) ( ) ( 2 1 x f x f  ) ( ) ( 2 1 x f x f  2 1 x x  ) ( ) ( 2 1 x f x f  ) ( ) ( 2 1 x f x f 

7 слайд

• Егер у = f(х) функциясының анықталу облысындағы кез келген сандары үшін теңсіздігі орындалса, онда функция өспелі , ал теңсіздігі орындалса, онда ол кемімелі деп аталады • Егер у = f(х) функциясының анықталу облысындағы кез келген сандары үшін теңсіздігі орындалса, онда функция кемімейтін , ал теңсіздігі орындалса, онда ол өспейтін функция деп аталады. Өспелі, кемімелі, кемімейтін, өспейтін функцияларды бірсарынды(монотонды) функциялар деп атайды. • а нүктесінің аймағы деп осы нүктені қамтитын кез келген аралықта айтады. Анықтама2 1 x x  ) ( ) ( 2 1 x f x f  ) ( ) ( 2 1 x f x f  2 1 x x  ) ( ) ( 2 1 x f x f  ) ( ) ( 2 1 x f x f 

8 слайд
• Егер нүктесінің қандай да бір аймағынан алынған барлық х үшін теңсіздігі орындалса, онда нүктесі f(х) функциясының минимум , ал теңсіздігі орындалса, максимум нүктесі деп аталады. Минимум және максимум нүктелерін экстремум нүктелері деп атайды. 1-суретАнықтама0 x ) ( ) ( 0x f x f  0 x ) ( ) ( 0x f x f 

8 слайд

• Егер нүктесінің қандай да бір аймағынан алынған барлық х үшін теңсіздігі орындалса, онда нүктесі f(х) функциясының минимум , ал теңсіздігі орындалса, максимум нүктесі деп аталады. Минимум және максимум нүктелерін экстремум нүктелері деп атайды. 1-суретАнықтама0 x ) ( ) ( 0x f x f  0 x ) ( ) ( 0x f x f 

9 слайд
• Егер у = f(х ) функциясы Х анықталу облысында бірсарынды өспелі(кемімелі) функция болса, онда осы функцияның У мәндер жиынында анықталған бірсарынды өспелі(бірсарынды кемімелі) функция оның кері функциясы болады. • Егер f функциясының анықталу облысы g функциясының мәндерінің облысы болса, f функциясының мәндерінің облысы g функциясының анықталу облысы болса, онда g функциясы f функциясына кері функция деп аталады • D(f)=E(g) және D(g)=E(f) Анықтама

9 слайд

• Егер у = f(х ) функциясы Х анықталу облысында бірсарынды өспелі(кемімелі) функция болса, онда осы функцияның У мәндер жиынында анықталған бірсарынды өспелі(бірсарынды кемімелі) функция оның кері функциясы болады. • Егер f функциясының анықталу облысы g функциясының мәндерінің облысы болса, f функциясының мәндерінің облысы g функциясының анықталу облысы болса, онда g функциясы f функциясына кері функция деп аталады • D(f)=E(g) және D(g)=E(f) Анықтама

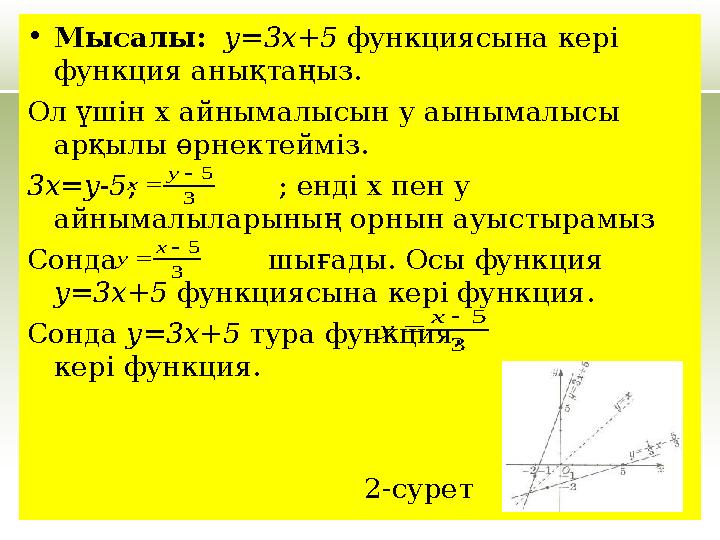
10 слайд
• Мысалы: у =3 x +5 функциясына кері функция анықтаңыз. Ол үшін х айнымалысын у аынымалысы арқылы өрнектейміз. 3 x = y -5 ; ; енді х пен у айнымалыларының орнын ауыстырамыз Сонда шығады. Осы функция у =3 x +5 функциясына кері функция. Сонда у =3 x +5 тура функция, кері функция. 2-сурет3 5   y x 3 5   х у 3 5   х у

10 слайд

• Мысалы: у =3 x +5 функциясына кері функция анықтаңыз. Ол үшін х айнымалысын у аынымалысы арқылы өрнектейміз. 3 x = y -5 ; ; енді х пен у айнымалыларының орнын ауыстырамыз Сонда шығады. Осы функция у =3 x +5 функциясына кері функция. Сонда у =3 x +5 тура функция, кері функция. 2-сурет3 5   y x 3 5   х у 3 5   х у

11 слайд

12 слайд