Геометриялық прогрессия

1 слайд
«Геометриялық «Геометриялық прогрессия»прогрессия»

1 слайд

2 слайд
ТАҚЫРЫПТЫ ОҚЫТУ НӘТИЖЕСІНДЕ КЕРЕКТАҚЫРЫПТЫ ОҚЫТУ НӘТИЖЕСІНДЕ КЕРЕК  - геометриялық - геометриялық прогрессияның n-ші прогрессияның n-ші мүшесін табу;мүшесін табу;  - геометриялық - геометриялық прогрессияның еселігі мен прогрессияның еселігі мен бірінші мүшесін табу;бірінші мүшесін табу;  - геометриялық - геометриялық прогрессияның алғашқы n прогрессияның алғашқы n мүшесінің қосындысын мүшесінің қосындысын табу;табу;  - шексіз кемімелі - шексіз кемімелі геометриялық геометриялық прогрессияның прогрессияның қосындысын табу.қосындысын табу. - геометриялық прогрессияның анықтамасы ; - геометриялық прогрессияның еселігін анықтау; - геометриялық прогрессияның n-ші мүшесінің формуласын; - геометриялық прогрессияның алғашқы n мүшесінің қосындысын формуласы; - шексіз кемімелі геометриялық прогрессияның қосындысы. БІЛУ: ІСТЕУ: БІЛУ: ІСТЕУ:

2 слайд

3 слайд
 Тексеруден өтуді, ақ шеттеріне Тексеруден өтуді, ақ шеттеріне белгі қоюды, тақырыптың белгі қоюды, тақырыптың рейтінгілік парағын толтыруды рейтінгілік парағын толтыруды ұмытпа.ұмытпа.  Өзіңде пайда болған сұрақтарды Өзіңде пайда болған сұрақтарды жауапсыз қалдырма.жауапсыз қалдырма.  Өзара тексеру кезінде объективті Өзара тексеру кезінде объективті бол, бұл саған да, тексерушіге де бол, бұл саған да, тексерушіге де көмегін тигізеді.көмегін тигізеді. Алгоритм бойынша жұмыс істеу керек Алгоритм бойынша жұмыс істеу керек екенін есіңде сақта!екенін есіңде сақта!

3 слайд

4 слайд
№1 №2 №3 №4 №5 №6 ТапсырмаларТапсырмалар РЕЙТИНГІЛІК ПАРАҚРЕЙТИНГІЛІК ПАРАҚ

4 слайд

5 слайд
1) Ауызша сұрақтарға жауап бер: - Қандай сан тізбегін геометриялық прогрессия деп атайды? (1б) - Геометриялық прогрессияның еселігі деген не? (1б) - Геометриялық прогрессияның n-ші мүшесінің формуласы. (1б) 2) Берілген сандық тізбектерден геометриялық прогрессияны тап: а) 2;6;18;54;...... б) 3;12;49;...... в) -7;35;-175;875;..... г)-14;-22;-44;-88;...... Өз таңдауыңды ауызша түсіндір. (2б) 3) Геометриялық прогрессияға ойдан үш мысал құрып, дәптеріне жаз. (2б) 4) Жаз: - Геометриялық прогрессия еселігінің формуласын. (1б) - Геометриялық прогрессияның n-ші мүшесінің формуласын. (1б) - Геометриялық прогрессияның 3-ші, 5-ші, 8-ші, 17-ші, 21-ші мүшесін табу формуласын. (4б) №1 ТАПСЫРМА №№1 ТЕКСЕРУДЕН ӨТУ1 ТЕКСЕРУДЕН ӨТУ

5 слайд

6 слайд
№№2 ТАПСЫРМА2 ТАПСЫРМА  Геометриялық прогрессия {bn}: 1;3;9;27; берілген...... b1 мен q тап. Геометриялық прогрессия {bn}: 1;3;9;27; берілген...... b1 мен q тап. (2б)(2б)  Геометриялық прогрессия {сn} 6-шы мүшесін қалай табу керек, Геометриялық прогрессия {сn} 6-шы мүшесін қалай табу керек, егер с1=-2, q=1,5 болса.егер с1=-2, q=1,5 болса. (2б) (2б)  n-ші мүше формуласы бойынша геометриялық прогрессияның {хn} n-ші мүше формуласы бойынша геометриялық прогрессияның {хn} бірінші мүшесін тап, егер х6=-96, q=2 болса.бірінші мүшесін тап, егер х6=-96, q=2 болса. (2б) (2б)  Геометриялық прогрессияның n-ші мүше формуласын пайдаланып Геометриялық прогрессияның n-ші мүше формуласын пайдаланып {bn}, q еселігін тап, егер b1=1, b4=64 болса.{bn}, q еселігін тап, егер b1=1, b4=64 болса. (2б) (2б)  Кітабыңдағы « §13. Геометриялық прогрессияның алғашқы n Кітабыңдағы « §13. Геометриялық прогрессияның алғашқы n мүшесінің қосындысын табу» формуласын табу мәтінін оқып, q≠1 мүшесінің қосындысын табу» формуласын табу мәтінін оқып, q≠1 болғандағы формулаларды пайдаланып, ал q >1болғанда (5) және болғандағы формулаларды пайдаланып, ал q >1болғанда (5) және (6) формулалардың қайсысын қолдану ыңғайлы екенін дәлелде.(6) формулалардың қайсысын қолдану ыңғайлы екенін дәлелде.  1мысал. Геометриялық прогрессияда: 1мысал. Геометриялық прогрессияда: в1в1 = 4, = 4, qq = 3 болса, оның = 3 болса, оның алғашқы жеті мүшесінің қосындысын табу керек.алғашқы жеті мүшесінің қосындысын табу керек.  Шешімі: Кітапта берілген (6) формулаланы Шешімі: Кітапта берілген (6) формулаланы Sn = в1 (qn-1)/(q-1) Sn = в1 (qn-1)/(q-1) пайдаланамызпайдаланамыз. . Сонда Сонда S7 = в1 (q7 -1)/(q-1)= 4(37-1)/(3-1) = S7 = в1 (q7 -1)/(q-1)= 4(37-1)/(3-1) = 4372.4372.  6) 6) Геометриялық прогрессияның алғашқы n мүшесінің қосындысын Геометриялық прогрессияның алғашқы n мүшесінің қосындысын табу үшін екі формуланы дәптерге теріп жаз. Оларды жаттап ал. табу үшін екі формуланы дәптерге теріп жаз. Оларды жаттап ал. (2б)(2б) №№2 ТЕКСЕРУДЕН ӨТУ2 ТЕКСЕРУДЕН ӨТУ

6 слайд

7 слайд
№№3 ТАПСЫРМА3 ТАПСЫРМА Тапсырмалардың біреуін орында:Тапсырмалардың біреуін орында:  Геометриялық прогрессияның 5-ші мүшесін тап: Геометриялық прогрессияның 5-ші мүшесін тап:  а) 81;27;9;...... б)-64;32;-16;...а) 81;27;9;...... б)-64;32;-16;... (2б) (2б)  Бір мысалды таңдап шығар: Бір мысалды таңдап шығар: (6б)(6б)  А) А) 1) b7 қалай табу керек, егер b1=15, q=2;1) b7 қалай табу керек, егер b1=15, q=2;  2) b13, егер b1=9, q=1/3;2) b13, егер b1=9, q=1/3;  3) b5, егер b1=20, q=1/2;3) b5, егер b1=20, q=1/2;  4) b9, егер b1=1, q=-3.4) b9, егер b1=1, q=-3.  Б) Б) {bn} геометриялық прогрессияның бірінші мүшесі және еселігі берілген болса, bn-ді табыңдар.{bn} геометриялық прогрессияның бірінші мүшесі және еселігі берілген болса, bn-ді табыңдар.  1) b1=2, q=-3, n=4;1) b1=2, q=-3, n=4;  2) b1=16, q=0,5, n=5;2) b1=16, q=0,5, n=5;  3) b1=100, q=-1/10, n=3;3) b1=100, q=-1/10, n=3;  4) b1=3/5, q=1/5, n=4.4) b1=3/5, q=1/5, n=4.  В) В) q еселігін қалай табуға болады, егер: q еселігін қалай табуға болады, егер:  1) b1=1, b4=64;1) b1=1, b4=64;  2) b1=2, b5=162;2) b1=2, b5=162;  3) b1=5, b4=1.3) b1=5, b4=1.  Геометриялық прогрессияның бірінші мүшелерінің n-қосындысының формуласын пайдаланып, келесі Геометриялық прогрессияның бірінші мүшелерінің n-қосындысының формуласын пайдаланып, келесі мысалдарды шеш:мысалдарды шеш: (8б) (8б)  А) А) геометриялық прогрессияның бірінші 10 мүшелерінің қосындысын тап{хn}:геометриялық прогрессияның бірінші 10 мүшелерінің қосындысын тап{хn}:  1)27;9;.... 2) 12;24;...1)27;9;.... 2) 12;24;...  Б) Б) геометриялық прогрессияның бірінші 15 мүшелерінің қосындысын тап{bn}:геометриялық прогрессияның бірінші 15 мүшелерінің қосындысын тап{bn}:  1) b1=1, b5=81; 2) b1=2, b5=64.1) b1=1, b5=81; 2) b1=2, b5=64. №№3 ТЕКСЕРУДЕН ӨТУ3 ТЕКСЕРУДЕН ӨТУ

7 слайд

8 слайд
№№4 ТАПСЫРМА4 ТАПСЫРМА Мысалды шешу үлгісін қара: Мысалды шешу үлгісін қара: шексіз кемімелі геометриялық прогрессияның қосындысы 9, ал ал шексіз кемімелі геометриялық прогрессияның қосындысы 9, ал ал мүшелерінің квадраттарының қосындысы 40,5. Прогрессияның бірінші мүшесі мен мүшелерінің квадраттарының қосындысы 40,5. Прогрессияның бірінші мүшесі мен еселігін тап.еселігін тап. Шешімі:Шешімі: есеп шарты бойынша прогрессияның еселігі есеп шарты бойынша прогрессияның еселігі qq, ал квадраттарының еселігі , ал квадраттарының еселігі q2 q2 олай олай болса, болса, b1/1-q=9, b12/1-q2=40,5. b1/1-q=9, b12/1-q2=40,5. Бұлардан Бұлардан b1=9(1-q)b1=9(1-q) болса, мұны екінші теңдік орнына болса, мұны екінші теңдік орнына қойсақ қойсақ 81(1-q2)/ 1-q2=40,5 81(1-q2)/ 1-q2=40,5 бұданбұдан 1+q=2(1-q), q=1/3; b1=9(1-1/3)=6. 1+q=2(1-q), q=1/3; b1=9(1-1/3)=6. 2) Осы сияқты бір мысалды таңдап шеш. (2б)2) Осы сияқты бір мысалды таңдап шеш. (2б) А) А) Егер алғашқы 6 мүшесінің қосындысы 1820, еселігі 3 болатын геометриялық Егер алғашқы 6 мүшесінің қосындысы 1820, еселігі 3 болатын геометриялық прогрессияның бірінші және бесінші мүшесін тап. прогрессияның бірінші және бесінші мүшесін тап. ВВ)) Төрт сан геометриялық прогрессия құрайды. Егер әрбір мүшеге 1;1;4 және 13 Төрт сан геометриялық прогрессия құрайды. Егер әрбір мүшеге 1;1;4 және 13 сандарын сәйкес қосады, содан шыққан сандар арифметикалық прогрессия құрайды. Осы сандарын сәйкес қосады, содан шыққан сандар арифметикалық прогрессия құрайды. Осы сандарды тап.сандарды тап. 3)3) АА және және ББ бір тапсырмадан орында. бір тапсырмадан орында. (4б) (4б) А)А) {an} геометриялық прогрессияның алғашқы 6 мүшесін анықта. а1=-24,q=-1,5 {an} геометриялық прогрессияның алғашқы 6 мүшесін анықта. а1=-24,q=-1,5 Б)Б) Егер в1=1, в4=64 болса, онда Егер в1=1, в4=64 болса, онда {{в4в4}} геометриялық прогрессияның еселігін тап. геометриялық прогрессияның еселігін тап. 4)4) Геометриялық прогрессияның алғашқы 8 мүшесінің қосындысы 85/64 – не, ал Геометриялық прогрессияның алғашқы 8 мүшесінің қосындысы 85/64 – не, ал еселігі q=-1/2 – ге тең. Оның бірінші мүшесін тап.еселігі q=-1/2 – ге тең. Оның бірінші мүшесін тап. (6б) (6б) 5) А5) А және және ББ бір тапсырмаларының біреуін шеш. бір тапсырмаларының біреуін шеш. (4б) (4б) А) 1А) 1;3;32; ;3;32; ... геометриялық прогрессияның ... геометриялық прогрессияның nn мүшесінің қосындысын тап. мүшесінің қосындысын тап. Б) Егер геометриялық прогрессия үшін S2=4 және S3=13 болса, S5-ті тап.Б) Егер геометриялық прогрессия үшін S2=4 және S3=13 болса, S5-ті тап. №№4 ТЕКСЕРУДЕН ӨТУ4 ТЕКСЕРУДЕН ӨТУ

8 слайд

9 слайд
№№5 ТАПСЫРМА5 ТАПСЫРМА №№5 ТЕКСЕРУДЕН ӨТУ5 ТЕКСЕРУДЕН ӨТУ

9 слайд

10 слайд
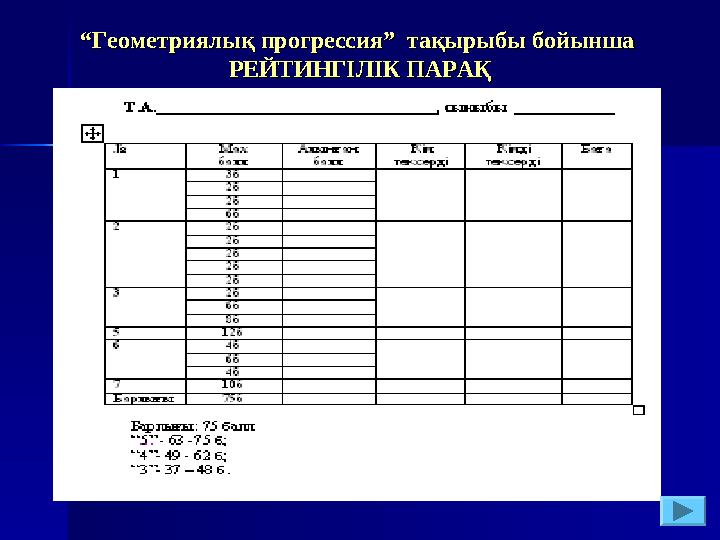
№№66 ТАПСЫРМАТАПСЫРМА №№6 ТЕКСЕРУДЕН ӨТУ6 ТЕКСЕРУДЕН ӨТУ Барлығы: 10 балл “5” – 10б; “4” -8б; “3” -6б.

10 слайд

11 слайд
““Геометриялық прогрессияГеометриялық прогрессия”” тақырыбы бойынша тақырыбы бойынша РЕЙТИНГІЛІК ПАРАҚРЕЙТИНГІЛІК ПАРАҚ

11 слайд

12 слайд
Сау болыңыздар!!!

12 слайд