Ашық сабақ, ҚМЖ, көрнекілік, презентация жариялап
2 млн. ₸ табыс табыңыз!
МИНИСТРЛІКПЕН КЕЛІСІЛГЕН КУРСҚА ҚАТЫСЫП, АТТЕСТАЦИЯҒА ЖАРАМДЫ СЕРТИФИКАТ АЛЫҢЫЗ!
Сертификат Аттестацияға 100% жарамды
ТОЛЫҚ АҚПАРАТ АЛУ 
Квадрат түбірі бар өрнектерді түрлендіру
Материал туралы қысқаша түсінік
Квадрат түбірі бар өрнектерді түрлендіру тақырыбына слайд
Авторы:
Автор материалды ақылы түрде жариялады.
Сатылымнан түскен қаражат авторға автоматты түрде аударылады.
Толығырақ
07 Ақпан 2024
203
0 рет жүктелгенТегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!
Дипломдар мен сертификаттарды алып үлгеріңіз!
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 17
Материалдың қысқаша түсінігі
1 слайд
КВАДРАТ ТҮБІРІ
БАР ӨРНЕКТЕРДІ
ТҮРЛЕНДІРУ
1 слайд
КВАДРАТ ТҮБІРІ БАР ӨРНЕКТЕРДІ ТҮРЛЕНДІРУ
2 слайд
Квадрат түбір қасиеттерін
еске түсірейік
2 слайд
Квадрат түбір қасиеттерін еске түсірейік
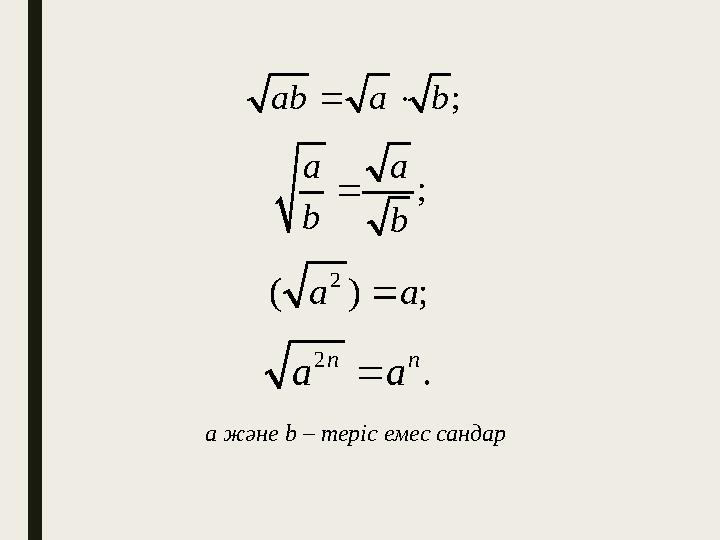
3 слайд
2
( ) ; a a
; ab a b
;
a a
b b
2
.
n n
a a а және b – теріс емес сандар
3 слайд
2 ( ) ; a a ; ab a b ; a a b b 2 . n n a a а және b – теріс емес сандар
4 слайд
4 слайд
5 слайд
5 слайд
6 слайд
1 мысал: Өрнекті ықшамдаңдар:2 4
) a a b
2 4
a b
2
; ab
4
6
16
)
9
a
б
b
4
6
16
9
a
b
2
3
4
.
3
a
b
2 мысал: Көбейткішті түбір таңбасының алдына
шығару:
) 81 a a 81 a 9 ; a
2
) 32 б a
2
16 2 a
2
16 2 a 4 2; a
7 5
) 9 в a b
6 4
9 a a b b
6 4
9 a a b b
3 2
3 . a b ab
6 слайд
1 мысал: Өрнекті ықшамдаңдар:2 4 ) a a b 2 4 a b 2 ; ab 4 6 16 ) 9 a б b 4 6 16 9 a b 2 3 4 . 3 a b 2 мысал: Көбейткішті түбір таңбасының алдына шығару: ) 81 a a 81 a 9 ; a 2 ) 32 б a 2 16 2 a 2 16 2 a 4 2; a 7 5 ) 9 в a b 6 4 9 a a b b 6 4 9 a a b b 3 2 3 . a b ab
7 слайд
3 мысал: Көбейткішті түбір таңбасының ішіне
енгізу) 2 2 a 4 2 4 2
3
)
3
a b
б
a
2
9
3
a b
a
2
9
3
a b
a
3 . ab
8
7 слайд
3 мысал: Көбейткішті түбір таңбасының ішіне енгізу) 2 2 a 4 2 4 2 3 ) 3 a b б a 2 9 3 a b a 2 9 3 a b a 3 . ab 8
8 слайд
4 мысал: Амалдарды орындау:) )( ( ) b a b a а
, x a . b y
( )( ) a b a b ( )( ) x y x y
2 2
. x y
2
, x a
2
. y b
( )( ) a b a b . a b
( )( ) a b a b
2 2
( ) ( ) a b . a b
2
) ( ) б a b
2 2
( ) 2 ( ) a a b b
2 . a ab b
8 слайд
4 мысал: Амалдарды орындау:) )( ( ) b a b a а , x a . b y ( )( ) a b a b ( )( ) x y x y 2 2 . x y 2 , x a 2 . y b ( )( ) a b a b . a b ( )( ) a b a b 2 2 ( ) ( ) a b . a b 2 ) ( ) б a b 2 2 ( ) 2 ( ) a a b b 2 . a ab b
9 слайд
5 мысал : Көбейткіштерге жіктеу:) 4 4 а a ab b
2 2
2 2 2 . a a b b
4 4 a ab b
2
2 . a b
) 1 б x x
2
1 x x
3
3
1 . x
3 3 2 2
( )( ) a b a b a ab b
, a x 1. b
3
3
1 x
2
2
1 1 1 x x x
2
1 1 . x x x
9 слайд
5 мысал : Көбейткіштерге жіктеу:) 4 4 а a ab b 2 2 2 2 2 . a a b b 4 4 a ab b 2 2 . a b ) 1 б x x 2 1 x x 3 3 1 . x 3 3 2 2 ( )( ) a b a b a ab b , a x 1. b 3 3 1 x 2 2 1 1 1 x x x 2 1 1 . x x x
10 слайд
6 мысал : Өрнекті ықшамдау:
2
3 3
3 .
3 3
a a
a
a a
1) 3 3 a a
3 3
3 a
2 2
3 3 3 a a a
3 3 3 ; a a a
2
2) 3 3 a a
2 2
2 3 3 3 a a a
2 3 3 3 a a a 3 3. a a
3 3 3
3)
3 3
a a a
a a
3. a
4) 3 3 a a
2 2
3 a 3. a
10 слайд
6 мысал : Өрнекті ықшамдау: 2 3 3 3 . 3 3 a a a a a 1) 3 3 a a 3 3 3 a 2 2 3 3 3 a a a 3 3 3 ; a a a 2 2) 3 3 a a 2 2 2 3 3 3 a a a 2 3 3 3 a a a 3 3. a a 3 3 3 3) 3 3 a a a a a 3. a 4) 3 3 a a 2 2 3 a 3. a
11 слайд
7 мысал: Берілген алгебралық өрнекті
бөлшектің бөлімінде квадрат түбір таңбасы
болмайтындай етіп түрлендіру: 1
)
2
a
Бөлшектің бөлімін және алымын бір мезгілде
нөлден өзгеше санға немесе өрнекке көбейтсек,
бөлшектің мәні өзгермейді
1
2
1 2
2 2
2
2
2
2
.
2
1
)
3 2
б
1 3 2
3 2 3 2
2 2
3 2
3 2
3 2
3 2
3 2.
2 3
1
)
б
11 слайд
7 мысал: Берілген алгебралық өрнекті бөлшектің бөлімінде квадрат түбір таңбасы болмайтындай етіп түрлендіру: 1 ) 2 a Бөлшектің бөлімін және алымын бір мезгілде нөлден өзгеше санға немесе өрнекке көбейтсек, бөлшектің мәні өзгермейді 1 2 1 2 2 2 2 2 2 2 . 2 1 ) 3 2 б 1 3 2 3 2 3 2 2 2 3 2 3 2 3 2 3 2 3 2. 2 3 1 ) б
12 слайд
- егер бөлшектің бөлімі түрінде болса, онда бөлшектің
алымын да, бөлімін де -ға көбейту керекЕгер алгебралық бөлшектің бөлімінде түбір таңбасы
тұратын болса, онда
бөлшектің бөлімі иррационалдықты құрайды
деп айтады.
Өрнекті бөлшектің бөлімінде түбір таңбасы
болмайтындай етіп түрлендіруді
бөлшектің бөлімін иррационалдықтан құтқару
деп атайды.
-
егер бөлшектің бөлімі немесе түрде болса,
онда бөлшектің бөлімін де, алымын да сәйкесінше
немесе (түйіндес өрнекке)
көбейту керек а
а b а b
а b а b а
12 слайд
- егер бөлшектің бөлімі түрінде болса, онда бөлшектің алымын да, бөлімін де -ға көбейту керекЕгер алгебралық бөлшектің бөлімінде түбір таңбасы тұратын болса, онда бөлшектің бөлімі иррационалдықты құрайды деп айтады. Өрнекті бөлшектің бөлімінде түбір таңбасы болмайтындай етіп түрлендіруді бөлшектің бөлімін иррационалдықтан құтқару деп атайды. - егер бөлшектің бөлімі немесе түрде болса, онда бөлшектің бөлімін де, алымын да сәйкесінше немесе (түйіндес өрнекке) көбейту керек а а b а b а b а b а
13 слайд
8 мысал: Өрнекті ықшамдау:.
3 5
4
5 7
2
7
7
7
7
) 1
7 7
7 7
7
7 7
; 7
5 7
2
) 2
5 7 5 7
5 7 2
2 2
5 7
5 7 2
5 7
5 7 2
2
5 7 2
; 5 7
3 5
4
) 3
3 5 3 5
3 5 4
2 2
3 5
3 5 4
3 5
3 5 4
2
3 5 4
; 3 5 2
) 3 5 ( 2 ) 5 7 ( 7 ) 4 3 2 5 2 5 7 7
. 3 2 5
13 слайд
8 мысал: Өрнекті ықшамдау:. 3 5 4 5 7 2 7 7 7 7 ) 1 7 7 7 7 7 7 7 ; 7 5 7 2 ) 2 5 7 5 7 5 7 2 2 2 5 7 5 7 2 5 7 5 7 2 2 5 7 2 ; 5 7 3 5 4 ) 3 3 5 3 5 3 5 4 2 2 3 5 3 5 4 3 5 3 5 4 2 3 5 4 ; 3 5 2 ) 3 5 ( 2 ) 5 7 ( 7 ) 4 3 2 5 2 5 7 7 . 3 2 5
14 слайд
Шығармашылық тапсырма :
Сыртқы түбір белгісінен босату керек :
14 слайд
Шығармашылық тапсырма : Сыртқы түбір белгісінен босату керек :
15 слайд
Бағалар критерийі:
6-7 тапсырма дұрыс
–“ 3 ”
8-9 тапсырма дұрыс
–“ 4 ”
10 тапсырма дұрыс –“ 5 ”
15 слайд
Бағалар критерийі: 6-7 тапсырма дұрыс –“ 3 ” 8-9 тапсырма дұрыс –“ 4 ” 10 тапсырма дұрыс –“ 5 ”
16 слайд
Үй тапсырмасы :
•
Тест бойынша қатемен жұмыс.
•
Оқулықтағы немесе мұғалім берген
қосымша тапсырмаларды орындап келу.
•
Жіберген қателерді талдай отырып,
1-тарауды қайталап келу .
16 слайд
Үй тапсырмасы : • Тест бойынша қатемен жұмыс. • Оқулықтағы немесе мұғалім берген қосымша тапсырмаларды орындап келу. • Жіберген қателерді талдай отырып, 1-тарауды қайталап келу .
