Леонард Эйлердің ғылыми еңбектері

1 слайд
МатематикаМатематика Леонард Эйлердің Леонард Эйлердің ғылыми еңбектеріғылыми еңбектері Тойлыбаева Г

1 слайд

2 слайд
Леонард ЭйлерЛеонард Эйлер (1707 -1783)(1707 -1783) – – швейцар математигі, швейцар математигі, механигі әрі физигі. механигі әрі физигі. 20 жасынан бастап (1727-20 жасынан бастап (1727- 1741) Ресейде тұрған. 1727-1741) Ресейде тұрған. 1727- 1741жж. Петербургте 14 жыл еңбек етіп, 50 ден 1741жж. Петербургте 14 жыл еңбек етіп, 50 ден аса еңбек жазды. 1735 жылы бір көзінен, ал аса еңбек жазды. 1735 жылы бір көзінен, ал 1766ж. екінші көзінен айырылады. Шәкірттері – 1766ж. екінші көзінен айырылады. Шәкірттері – Котельников, Румовский, Фусс, Головин, Котельников, Румовский, Фусс, Головин, Сафронов. Сафронов.

2 слайд

3 слайд
Л. Эйлер 1741-1766жж. Берлинде вице-президент, Л. Эйлер 1741-1766жж. Берлинде вице-президент, математика қоғамының директоры болып, 1744ж. математика қоғамының директоры болып, 1744ж. «Максимум және минимум қасиеттері болатын қисық «Максимум және минимум қасиеттері болатын қисық сызықтарды табу» атты шығармасы жарық көрді. Бұл сызықтарды табу» атты шығармасы жарық көрді. Бұл вариациалық есептеуді баяндауға арналған бірінші еңбек вариациалық есептеуді баяндауға арналған бірінші еңбек болды. болды. Оның ішіндегі белгілілері:Оның ішіндегі белгілілері:

3 слайд

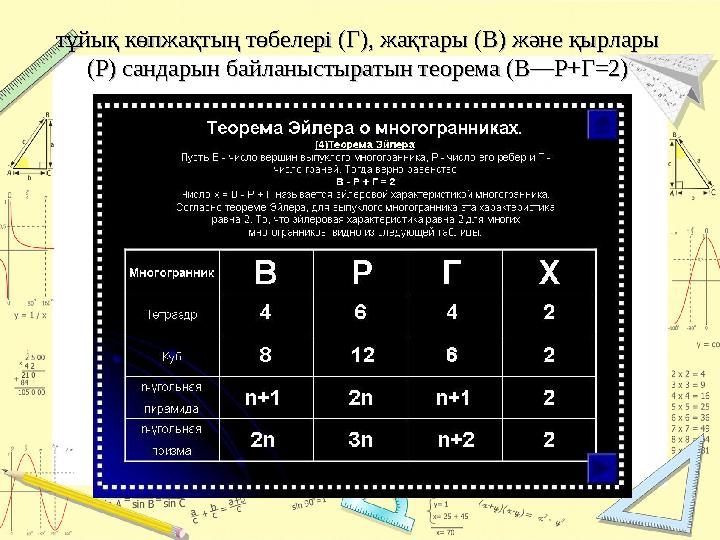
4 слайд
тұйық көпжақтың төбелері (Г), жақтары (В) және қырлары тұйық көпжақтың төбелері (Г), жақтары (В) және қырлары (Р) сандарын байланыстыратын теорема (В—Р+Г=2)(Р) сандарын байланыстыратын теорема (В—Р+Г=2)

4 слайд

5 слайд
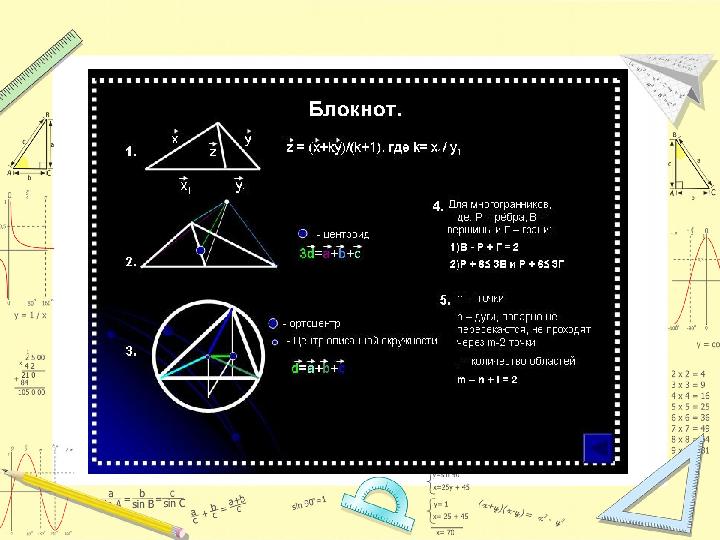
үшбұрыш ішіндегі Эйлер түзуіүшбұрыш ішіндегі Эйлер түзуі

5 слайд

6 слайд
тұрақты ені болатын қисықтартұрақты ені болатын қисықтар

6 слайд

7 слайд

7 слайд

8 слайд
Эйлер тұрақты саны: Эйлер тұрақты саны:

8 слайд

9 слайд
1748ж. «Шексіз аздар 1748ж. «Шексіз аздар анализіне кіріспе» жазды. Оның анализіне кіріспе» жазды. Оның екі томында шексіз қатарлар, екі томында шексіз қатарлар, оның ішінде оның ішінде ее хх , cos , cos xx , sin , sin xx қатарлары Иоганн Бернулли мен қатарлары Иоганн Бернулли мен басқалар әр түрлі формада басқалар әр түрлі формада тапқан тапқан ee ixix == coscos xx +sin+sin xx қатысы қатысы орын алған. Қисықтар мен орын алған. Қисықтар мен беттерді теңдеулер арқылы беттерді теңдеулер арқылы зерттеудің кемелдігіне және зерттеудің кемелдігіне және ұғымдылығына қарай бұл ұғымдылығына қарай бұл еңбекті аналитикалық геометрия еңбекті аналитикалық геометрия бойынша жазылған ең бірінші бойынша жазылған ең бірінші оқулық деуге болады. оқулық деуге болады.

9 слайд

10 слайд
Л. Эйлердің көлемі, мазмұны Л. Эйлердің көлемі, мазмұны жөнінен бай оқу нұсқасы – жөнінен бай оқу нұсқасы – «Дифференциалдық есептеу» «Дифференциалдық есептеу» 1755ж. жарық көрді. 1765ж. оның 1755ж. жарық көрді. 1765ж. оның «Қатты денелер қозғалысының «Қатты денелер қозғалысының теориясы» жарық көрді. Бұл теориясы» жарық көрді. Бұл трактатта нүктені айнала трактатта нүктені айнала қозғалған дененің теңдеулері қозғалған дененің теңдеулері келтірілген. келтірілген.

10 слайд

11 слайд
Ол 1766-1783жж. Петербургте еңбек етіп, 1768-Ол 1766-1783жж. Петербургте еңбек етіп, 1768- 1770жж. 3 томдық «Интегралдық есептеулер» еңбегін 1770жж. 3 томдық «Интегралдық есептеулер» еңбегін жазды. Бұл еңбектерде элементарлық дифференциалдық жазды. Бұл еңбектерде элементарлық дифференциалдық және интегралдық есептеуден басқа дифференциалдық және интегралдық есептеуден басқа дифференциалдық теңдеулерді интегралдау, Тейлор теоремасы және оның теңдеулерді интегралдау, Тейлор теоремасы және оның толып жатқан қолданыстары, Эйлердің қосындылау толып жатқан қолданыстары, Эйлердің қосындылау формуласы, Эйлер интегралдары бар.формуласы, Эйлер интегралдары бар.

11 слайд

12 слайд
Л. Эйлер 1768-1769жж. 2 Л. Эйлер 1768-1769жж. 2 томдық «Әмбебап томдық «Әмбебап арифметика» деген кітабын арифметика» деген кітабын жазды. Оның жатқа айтып жазды. Оның жатқа айтып отырып жаздырған «Алгебраға отырып жаздырған «Алгебраға толық кіріспе» (1770ж.) атты толық кіріспе» (1770ж.) атты еңбегі алгебра жөніндегі еңбегі алгебра жөніндегі көптеген кейінгі оқулықтарға көптеген кейінгі оқулықтарға үлгі болды. Мұнда алгебраның үлгі болды. Мұнда алгебраның үшінші және төртінші үшінші және төртінші дәрежелі теңдеулер дәрежелі теңдеулер теориясына дейін баяндалған.теориясына дейін баяндалған.

12 слайд

13 слайд

13 слайд

14 слайд
Л. Эйлердің 1769-1771жж. Л. Эйлердің 1769-1771жж. «Диоптрикасының» үш томы «Диоптрикасының» үш томы жарияланды. Мұнда линзалар жарияланды. Мұнда линзалар жүйесінде сәулелердің сыну теориясы жүйесінде сәулелердің сыну теориясы баяндалған. Оның еңбектерінің едәуір баяндалған. Оның еңбектерінің едәуір бөлігі астрономияға арналған. Әсіресе бөлігі астрономияға арналған. Әсіресе ол үш дене есебінің маңызды тарауы ол үш дене есебінің маңызды тарауы саналатын Ай қозғалысы теориясына саналатын Ай қозғалысы теориясына көп көңіл бөлген. Л. Эйлердің көп көңіл бөлген. Л. Эйлердің «Планеталар мен кометалар қозғалыс «Планеталар мен кометалар қозғалыс теориясы» (1774ж.) аспан теориясы» (1774ж.) аспан механикасына арналған. Оның 886-механикасына арналған. Оның 886- дан аса еңбектері бар.дан аса еңбектері бар.

14 слайд

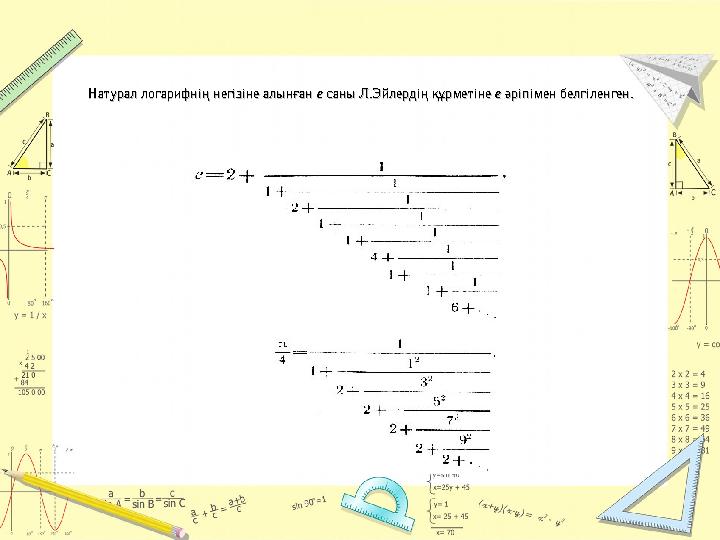
15 слайд
Натурал логарифнің негізіне алынған Натурал логарифнің негізіне алынған ее саны Л.Эйлердің құрметіне саны Л.Эйлердің құрметіне ее әріпімен белгіленген. әріпімен белгіленген.

15 слайд

16 слайд
Ол геометрия Ол геометрия саласында «топология» саласында «топология» деген жаңа ғылымын деген жаңа ғылымын зерттеп ашты. зерттеп ашты. Француз ғалымы Пьер Лаплас Француз ғалымы Пьер Лаплас Л.Эйлерді XVIII ғасырдың екінші Л.Эйлерді XVIII ғасырдың екінші жартысындағы «математиктердің жартысындағы «математиктердің баршасының ұстазы» деп қастер тұтқан.баршасының ұстазы» деп қастер тұтқан.

16 слайд

17 слайд

17 слайд