ОДНОФАЗНЫЙ ПЕРЕМЕННЫЙ ТОК

1 слайд
ЛЕКЦИЯ №2 ОДНОФАЗНЫЙ ПЕРЕМЕННЫЙ ТОК

1 слайд

2 слайд
1. Общие сведения ОПРЕДЕЛЕНИЕ: ЭДС, напряжение и ток называются переменными если их значения изменяются во времени. В современной технике получили применения переменные токи. Изменяющиеся во времени по синусоидальному закону, т.к. позволяют наиболее экономично осуществлять производство, распределение, преобразование и использование электрической энергии. Значения величин в данный момент времени называются МГНОВЕННЫМИ, они обозначаются малыми буквами: t , e , u , i , p . t , e , u , i , p – мгновенные значения ЭДС, напряжения, тока, мощности. Рассмотренные ранее законы Кирхгофа справедливы для мгновенных значений соответствующих величин. Применение однофазного переменного тока: 1) для питания осветительных установок, 2) систем сигнализации и контроля.

2 слайд

3 слайд
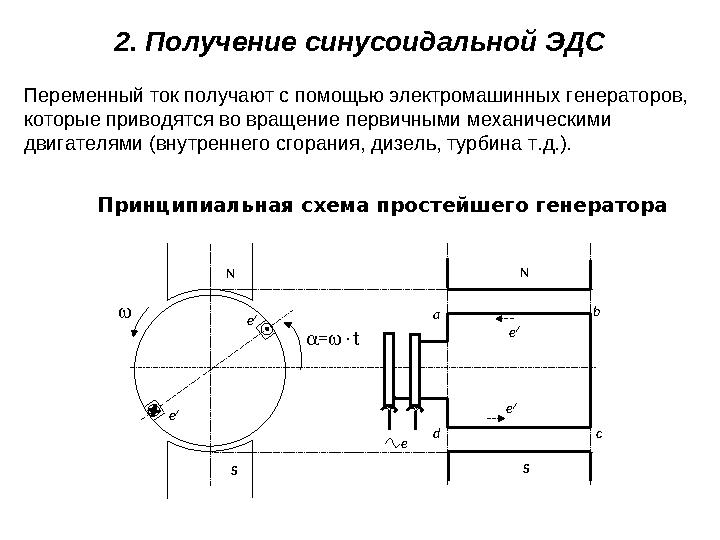
2. Получение синусоидальной ЭДС Переменный ток получают с помощью электромашинных генераторов, которые приводятся во вращение первичными механическими двигателями (внутреннего сгорания, дизель, турбина т.д.). Принципиальная схема простейшего генератора N S e / e / N Se / e / e a b cd =  t

3 слайд

4 слайд
; const  “ ab ” и “ cd ” – активные проводники ; / V l В е    ; sin sin t B B В M M       ; sin sin 2 2 2 / t E t V l В V l В е e M M               

4 слайд

5 слайд
Устройство синхронного генератора Между полюсами магнита вращается ферромагнитный сердечник с угловой скоростью  . В пазах сердечника расположен виток проволоки. Его концы присоединены к вращающимся контактным кольцам, к которым прижимаются неподвижные щетки, обеспечивающие связь неподвижных потребителей с вращающейся цепью. При вращении витка в его активных проводниках “ ab ” и “ cd ” по закону ЭМИ наводится ЭДС. Полюсам магнита придают специальную форму, чтобы магнитная индукция в зазоре вдоль окружности сердечника изменялась по синусоидальному закону. Активные проводники “ ab ” и “ cd ” витка соединены последовательно, поэтому результирующая ЭДС, снимаемая со щеток в два раза больше, чем в каждом из активных проводников. Принцип действия синхронного генератора

5 слайд

6 слайд
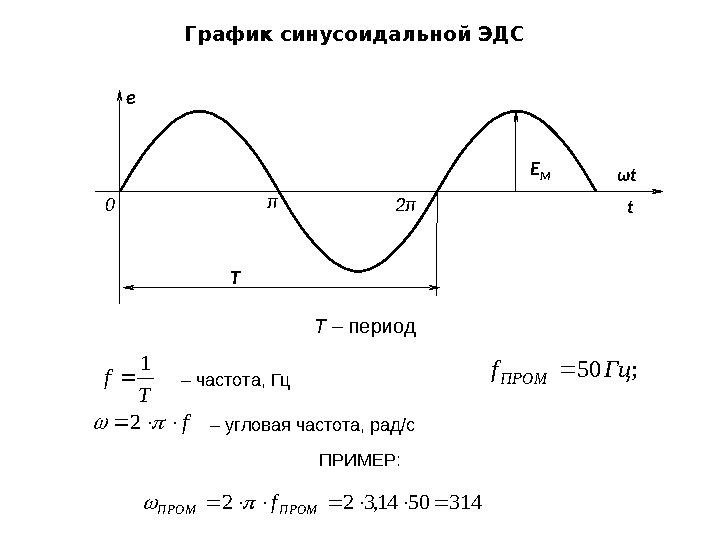
ωtе Е M π 2π0 Т tГрафик синусоидальной ЭДС Т – периодT f 1  – частота, Гц ; 50 Гц fПРОМ  f      2 – угловая частота, рад/с ПРИМЕР: 314 50 14,3 2 2        ПРОМ ПРОМ f  

6 слайд

7 слайд
Рассматривая работу элементарного генератора мы положили:; 0 ; 0    t В более общем случае справедлива зависимость ); sin(     t E е M  ; ) ( фаза t      ; ) ( фаза начальная   Если в пазах сердечника размещены два витка, сдвинутые относительно друг друга, то и индуктируемые ЭДС будут сдвинуты.

7 слайд

8 слайд
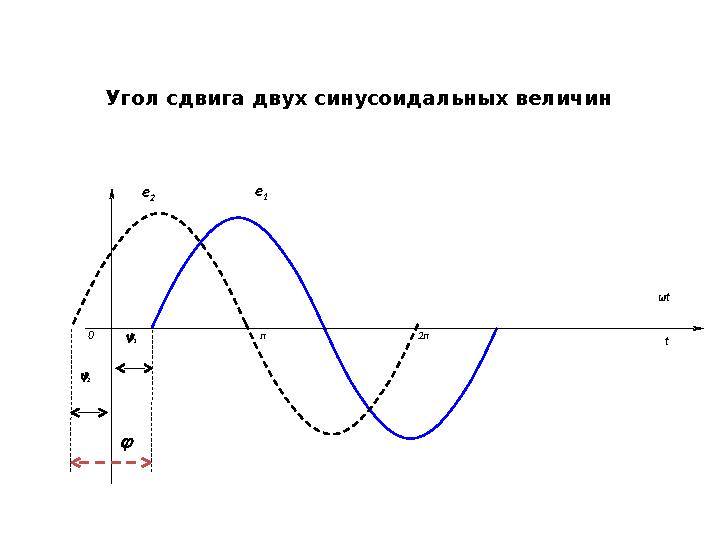
ωtе 2 π 2π0 1 tе 1  2  Угол сдвига двух синусоидальных величин

8 слайд

9 слайд
ОПРЕДЕЛЕНИЕ: Разность начальных фаз двух синусоидальных величин называется углом сдвига. Выделяют два случая: – то говорят, что функции совпадают по фазе; – то говорят, что функции находятся в противофазе;;2 1      0     

9 слайд

10 слайд
3. Действующие и средние значения синусоидальных величин О синусоидальных токах, напряжениях и ЭДС судят по их среднеквадратичным значениям. Рассмотрим синусоидальный ток Среднеквадратичное значение такого тока равно: ОПРЕДЕЛЕНИЕ: В Электротехнике среднеквадратичные значения тока, напряжения, ЭДС называется действующими. Под действующим значением переменного тока понимается такое значение постоянного тока, которое по тепловому действию за период эквивалентно переменному.; sin t I i M    ; 707. 0 2 sin 1 1 0 2 2 0 2 M M T M T I I dt t I T dt i T I          

10 слайд

11 слайд
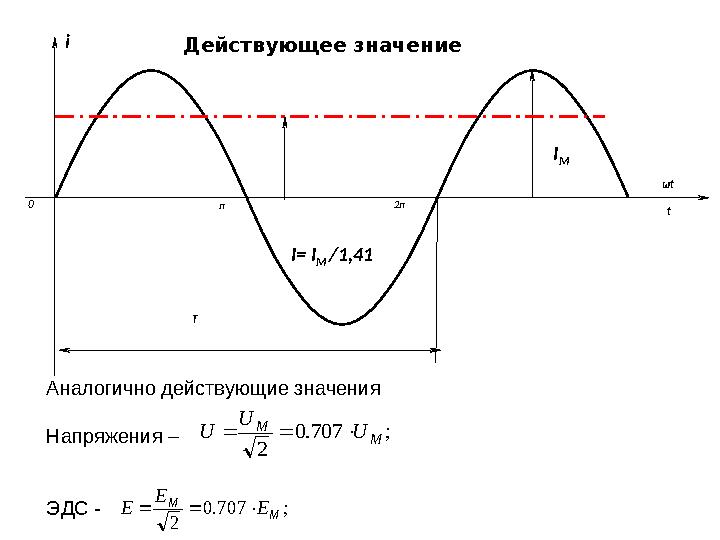
ωti I M π 2π0 Т tДействующее значение I = I M /1,41; 707. 0 2 M M U U U    ; 707.0 2 M M E E E    Аналогично действующие значения Напряжения – ЭДС -

11 слайд

12 слайд
ВАЖНО: Электроизмерительные приборы отградуированы в действующих значениях переменного тока. При анализе электровыпрямительных установок используются средние значения Рассмотрим синусоидальную ЭДС Среднее значение такой ЭДС равно:; sin t Е е M    ; 636. 0 sin 5, 0 1 5, 0 1 5,0 0 5,0 0 M T М T СР E dt t Е T еdt T Е               ; 636. 0 ; 636. 0 M СР M СР U U I I     Средние значение переменных тока и напряжения

12 слайд

13 слайд
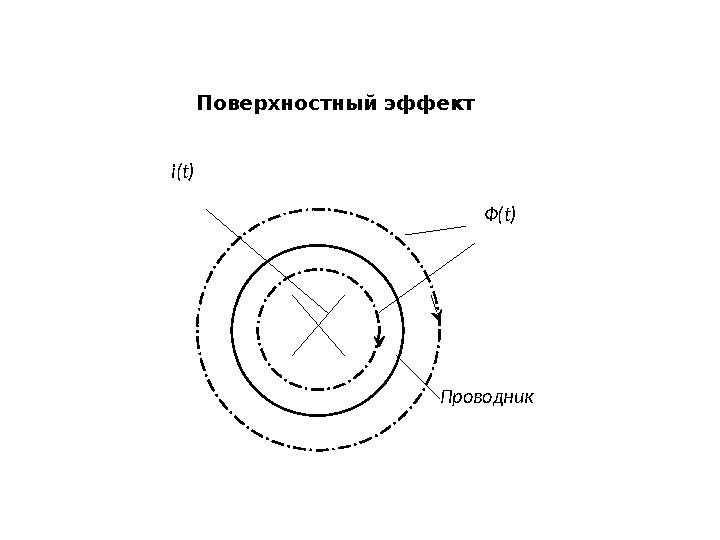
Ф (t)i(t) ПроводникПоверхностный эффект

13 слайд

14 слайд
5. Изображение синусоидальных величин с помощью вращающихся векторов При анализе работы электрических цепей переменного тока приходится складывать синусоидальные функции времени одной и той же частоты, но имеющие разные амплитуды и начальные фазы. Это удобно выполнять если синусоидальные функции изображать вращающимися векторами. Пусть нам задано мгновенное значение в виде:); sin(      t Е е M Рассмотрим два момента времени: t =0; t = t 1 ; Справа изобразим график синусоидальной ЭДС, слева – окружность, радиус которой ОА равен амплитудному значению ЭДС Е М . Радиус-Вектор ОА=Е М вращается с угловой скоростью  , равной угловой частоте изменения ЭДС. Тогда в любой момент времени по радиус-вектору можно определить мгновенный значения ЭДС, которые будут равны проекции длины вектора на вертикальную ось Y .

14 слайд

15 слайд
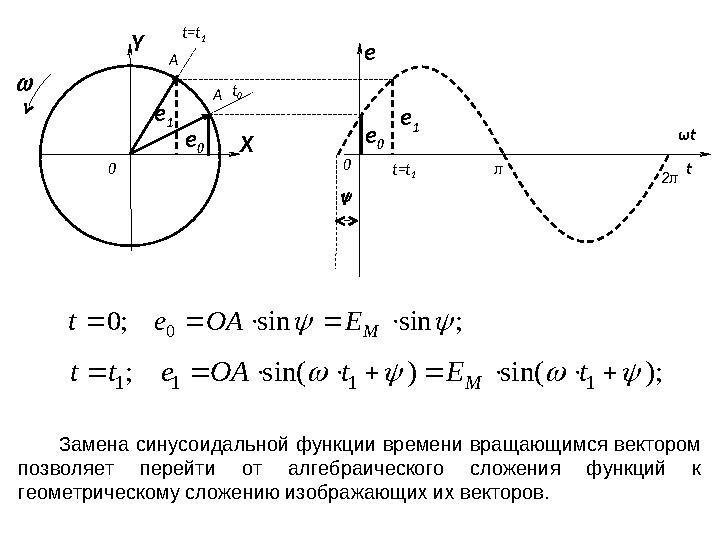
ωtе π 2π0 tе 1 е 0Y Х 0 е 0е 1 t=t 1t=t 1 t 0 AA  ; sin sin ; 0 0        M Е OA е t ); sin( ) sin( ; 1 1 1 1              t Е t OA е t t M Замена синусоидальной функции времени вращающимся вектором позволяет перейти от алгебраического сложения функций к геометрическому сложению изображающих их векторов.

15 слайд

16 слайд
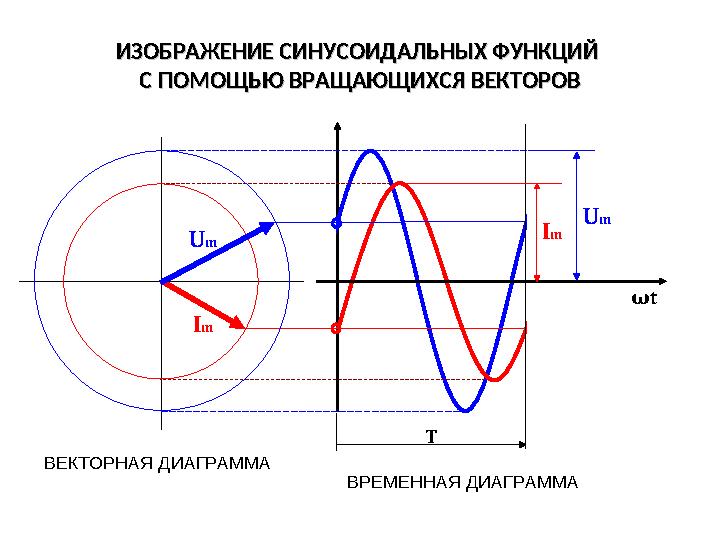
ИЗОБРАЖЕНИЕ СИНУСОИДАЛЬНЫХ ФУНКЦИЙ ИЗОБРАЖЕНИЕ СИНУСОИДАЛЬНЫХ ФУНКЦИЙ С ПОМОЩЬЮ ВРАЩАЮЩИХСЯ ВЕКТОРОВС ПОМОЩЬЮ ВРАЩАЮЩИХСЯ ВЕКТОРОВ U m I m U m I m ω t T ВЕКТОРНАЯ ДИАГРАММА ВРЕМЕННАЯ ДИАГРАММА

16 слайд

17 слайд
6. Векторные диаграммы Например, надо сложить синусоидально изменяющиеся во времени тока одной частоты Для этого необходимо на одном графике изобразить соответствующие вектора: ;3 2 1 i i i   ;3 2 1 I I I I M   

17 слайд

18 слайд
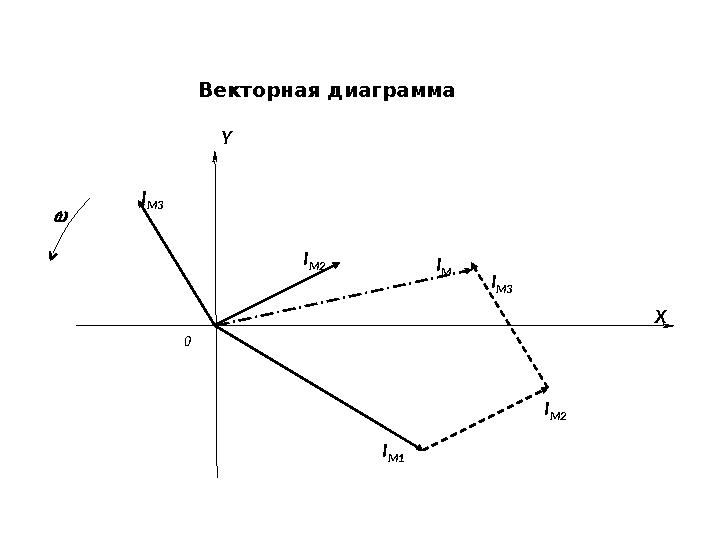
Y Х 0 I M 1I M2I M3 I M I M2I M3Векторная диаграмма

18 слайд

19 слайд
Результирующий вектор соответствует значению суммарного переменного тока. Его длина равна амплитудному значению результирующего тока. ОПРЕДЕЛЕНИЕ: Векторной диаграммой называется совокупность нескольких векторов, изображающих на одном графике синусоидальные функции времени одной частоты. На практике, при построении векторных диаграмм длину вектора принимают равной не амплитудному, а действующему значению. Один из векторов принимают за исходный, а остальные строятся по отношению к нему с соответствующим сдвигом фаз, при этом отпадает необходимость использовать оси Х и Y .

19 слайд