Презентация для онлайн урока "Решение тестовых задач с помощью дробных рациональных уравнений"
Презентация для онлайн урока "Решение тестовых задач с помощью дробных рациональных уравнений"


#1 слайд
Название предмета/Алгебра 8 класс
Тема урока/ Решение текстовых задач с помощью дробно-рациональных
уравнений
ФИО учителя/ Байсалова Куралай Неспековна
1 слайд
Название предмета/Алгебра 8 класс Тема урока/ Решение текстовых задач с помощью дробно-рациональных уравнений ФИО учителя/ Байсалова Куралай Неспековна

#2 слайд
Цель: рассмотреть типы задач,
решаемых с помощью дробных
рациональных уравнений, понятие
математической модели и этапы
решения задачи.
2 слайд
Цель: рассмотреть типы задач, решаемых с помощью дробных рациональных уравнений, понятие математической модели и этапы решения задачи.

#3 слайд
Понятие математической модели
•
Представление реальной ситуации на языке
математики с использованием различных правил,
свойств и законов математики называется
математической моделью задачи .
•
Различают несколько видов математических
моделей:
алгебраическая модель;
графическая модель;
геометрическая модель.
3 слайд
Понятие математической модели • Представление реальной ситуации на языке математики с использованием различных правил, свойств и законов математики называется математической моделью задачи . • Различают несколько видов математических моделей: алгебраическая модель; графическая модель; геометрическая модель.

#4 слайд
Этапы решения задачи
Первый этап. Составление математической
модели.
Вводится переменная, текст задачи переводится
на математический язык, составляется
уравнение.
Второй этап. Работа с математической моделью.
Решение уравнения.
Третий этап. Ответ на вопрос задачи.
Анализируя полученное решение, записывается
ответ на вопрос задачи.
4 слайд
Этапы решения задачи Первый этап. Составление математической модели. Вводится переменная, текст задачи переводится на математический язык, составляется уравнение. Второй этап. Работа с математической моделью. Решение уравнения. Третий этап. Ответ на вопрос задачи. Анализируя полученное решение, записывается ответ на вопрос задачи.

#5 слайд
Задачи, приводящие к решению дробных
рациональных уравнений
Задачи, в которых одна величина выражается через
другие при помощи дробного выражения:
•
Задачи на движение:
•
Задачи на работу:
5 слайд
Задачи, приводящие к решению дробных рациональных уравнений Задачи, в которых одна величина выражается через другие при помощи дробного выражения: • Задачи на движение: • Задачи на работу:
#6 слайд
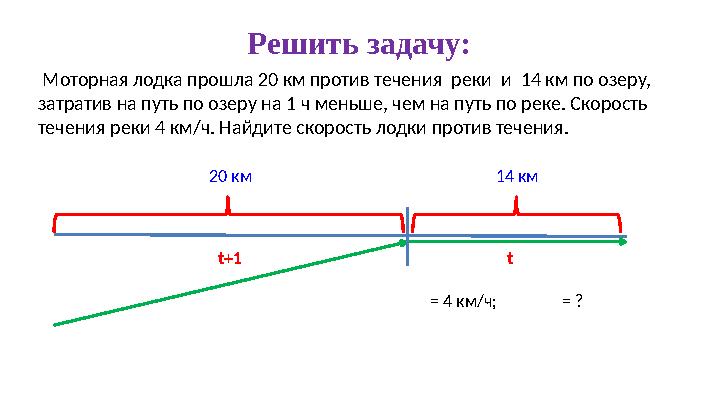
Решить задачу:
Моторная лодка прошла 20 км против течения реки и 14 км по озеру,
затратив на путь по озеру на 1 ч меньше, чем на путь по реке. Скорость
течения реки 4 км/ч. Найдите скорость лодки против течения .
20 км 14 км
t + 1 t
= 4 км/ч; = ?
6 слайд
Решить задачу: Моторная лодка прошла 20 км против течения реки и 14 км по озеру, затратив на путь по озеру на 1 ч меньше, чем на путь по реке. Скорость течения реки 4 км/ч. Найдите скорость лодки против течения . 20 км 14 км t + 1 t = 4 км/ч; = ?
#7 слайд
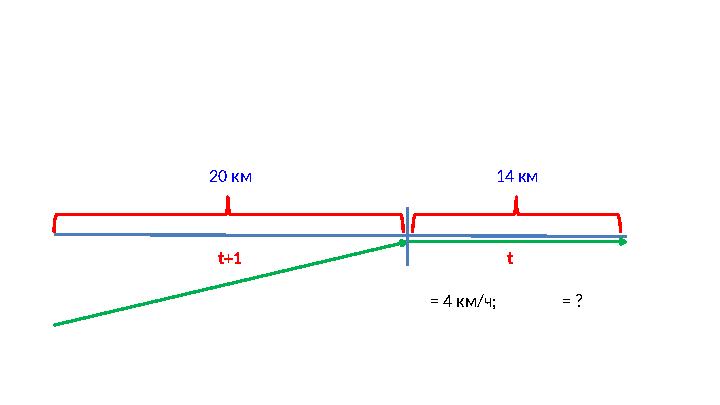
20 км 14 км
t+1 t
= 4 км/ч; = ?
7 слайд
20 км 14 км t+1 t = 4 км/ч; = ?
#8 слайд
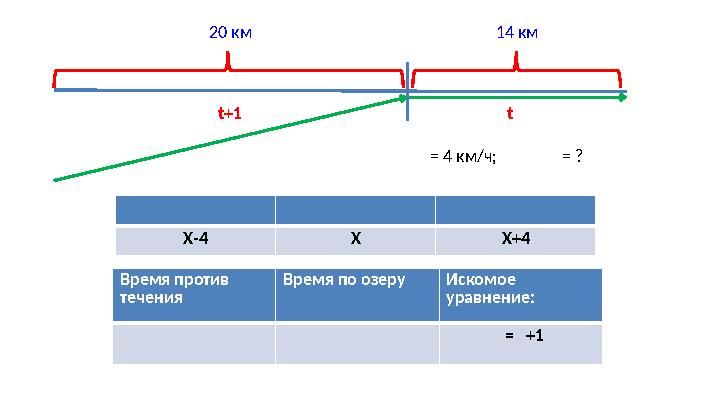
20 км 14 км
t+1 t
= 4 км/ч; = ?
Х-4 Х Х+4
Время против
течения Время по озеру Искомое
уравнение:
= +1
8 слайд
20 км 14 км t+1 t = 4 км/ч; = ? Х-4 Х Х+4 Время против течения Время по озеру Искомое уравнение: = +1
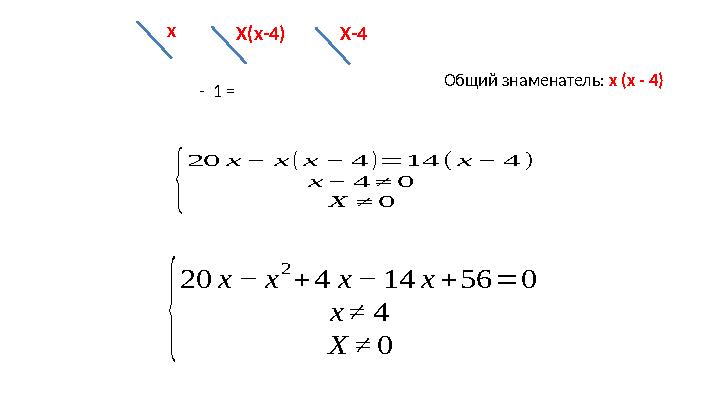
#9 слайд
- 1 = Общий знаменатель: х (х - 4)х
Х(х-4) Х-4{
20 х − х ( х − 4 )= 14 ( х − 4 )
х − 4 ≠ 0
Х ≠ 0
{
20 х − х
2
+ 4 х − 14 х + 56 = 0
х ≠ 4
Х ≠ 0
9 слайд
- 1 = Общий знаменатель: х (х - 4)х Х(х-4) Х-4{ 20 х − х ( х − 4 )= 14 ( х − 4 ) х − 4 ≠ 0 Х ≠ 0 { 20 х − х 2 + 4 х − 14 х + 56 = 0 х ≠ 4 Х ≠ 0
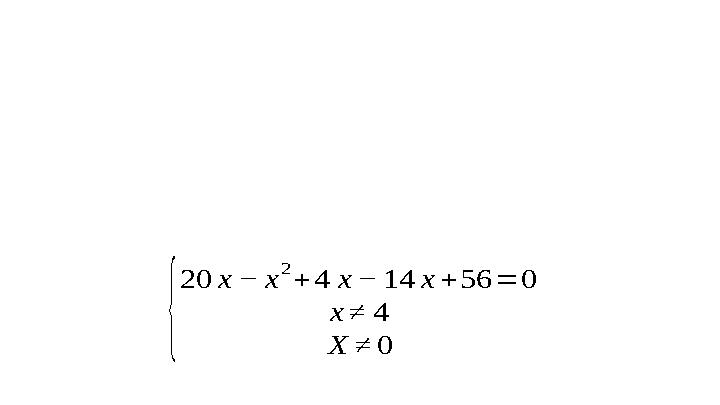
#10 слайд
{
20 х − х
2
+ 4 х − 14 х + 56 = 0
х ≠ 4
Х ≠ 0
10 слайд
{ 20 х − х 2 + 4 х − 14 х + 56 = 0 х ≠ 4 Х ≠ 0

#11 слайд
{
20 х − х
2
+ 4 х − 14 х + 56 = 0
х ≠ 4
Х ≠ 0
{
х
2
− 10 х − 56 = 0
х ≠ 4
Х ≠ 0По теореме Виета:
14 ; - 4
Скорость лодки: х = 14 км/час
Скорость лодки против течения: 14 - 4 = 10 км/час
11 слайд
{ 20 х − х 2 + 4 х − 14 х + 56 = 0 х ≠ 4 Х ≠ 0 { х 2 − 10 х − 56 = 0 х ≠ 4 Х ≠ 0По теореме Виета: 14 ; - 4 Скорость лодки: х = 14 км/час Скорость лодки против течения: 14 - 4 = 10 км/час

#12 слайд
Домашнее задание:
Решите уравнения3
1
3
х
х
3
5 3
5
х
х
5
3
3
3
2 2
y
y
y
y х
х
х
х
х
2
4
4
4
2
х
х
х
х
3
2
3
2
0
4 4
3
2 2
х
х х
х
х х
х
х
х
х 2 3
2
3 2
y
y
y
y 3 2
3
3
5
4
25
10
5
8 2
2
y
y
y y
y
12 слайд
Домашнее задание: Решите уравнения3 1 3 х х 3 5 3 5 х х 5 3 3 3 2 2 y y y y х х х х х 2 4 4 4 2 х х х х 3 2 3 2 0 4 4 3 2 2 х х х х х х х х х х 2 3 2 3 2 y y y y 3 2 3 3 5 4 25 10 5 8 2 2 y y y y y
#13 слайд
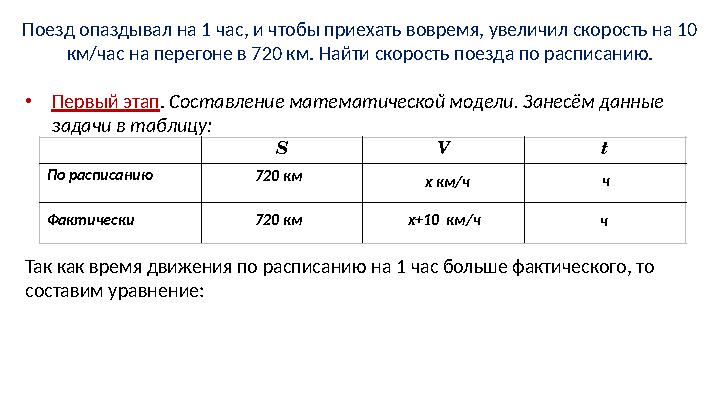
Поезд опаздывал на 1 час, и чтобы приехать вовремя, увеличил скорость на 10
км/час на перегоне в 720 км. Найти скорость поезда по расписанию.
•
Первый этап . Составление математической модели. Занесём данные
задачи в таблицу:
Так как время движения по расписанию на 1 час больше фактического, то
составим уравнение: S V t
По расписанию
Фактически 720 км
720 км x км/ч
x+10 км/ч ч
ч
13 слайд
Поезд опаздывал на 1 час, и чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию. • Первый этап . Составление математической модели. Занесём данные задачи в таблицу: Так как время движения по расписанию на 1 час больше фактического, то составим уравнение: S V t По расписанию Фактически 720 км 720 км x км/ч x+10 км/ч ч ч

#14 слайд
Поезд опаздывал на 1 час, и чтобы приехать вовремя, увеличил скорость
на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию.
•
Второй этап. Работа с математической моделью.
Решим уравнение:
При данных значениях x знаменатели дробей не равны нулю, значит эти
значения - корни составленного уравнения.
14 слайд
Поезд опаздывал на 1 час, и чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию. • Второй этап. Работа с математической моделью. Решим уравнение: При данных значениях x знаменатели дробей не равны нулю, значит эти значения - корни составленного уравнения.

#15 слайд
Поезд опаздывал на 1 час, и чтобы приехать вовремя,
увеличил скорость на 10 км/час на перегоне в 720 км.
Найти скорость поезда по расписанию.
•
Третий этап. Ответ на вопрос задачи.
Так как скорость поезда не может
выражаться отрицательным числом, то
значение не подходит условию задачи.
– скорость поезда по расписанию.
Ответ: 80 км/ч.
15 слайд
Поезд опаздывал на 1 час, и чтобы приехать вовремя, увеличил скорость на 10 км/час на перегоне в 720 км. Найти скорость поезда по расписанию. • Третий этап. Ответ на вопрос задачи. Так как скорость поезда не может выражаться отрицательным числом, то значение не подходит условию задачи. – скорость поезда по расписанию. Ответ: 80 км/ч.

#16 слайд
На изготовление 40 деталей первый рабочий тратит на 2
часа больше, чем второй на изготовление 36 деталей. Сколько
деталей в час делает первый рабочий, если известно, что
второй за час делает на 1 деталь больше?
•
Первый этап . Составление математической модели. Занесём данные
задачи в таблицу:
Так как первый рабочий на выполнение работы тратит на 2 часа больше, то
составим уравнение: работа производительность
( дет/час ) время
1-ый рабочий
2-ой рабочий 40
36 x
x+1
16 слайд
На изготовление 40 деталей первый рабочий тратит на 2 часа больше, чем второй на изготовление 36 деталей. Сколько деталей в час делает первый рабочий, если известно, что второй за час делает на 1 деталь больше? • Первый этап . Составление математической модели. Занесём данные задачи в таблицу: Так как первый рабочий на выполнение работы тратит на 2 часа больше, то составим уравнение: работа производительность ( дет/час ) время 1-ый рабочий 2-ой рабочий 40 36 x x+1

#17 слайд
На изготовление 40 деталей первый рабочий тратит на 2
часа больше, чем второй на изготовление 36 деталей. Сколько
деталей в час делает первый рабочий, если известно, что
второй за час делает на 1 деталь больше?
•
Второй этап. Работа с математической моделью.
Решим уравнение:
При данных значениях x знаменатели дробей не равны нулю, значит эти значения - корни
составленного уравнения.
17 слайд
На изготовление 40 деталей первый рабочий тратит на 2 часа больше, чем второй на изготовление 36 деталей. Сколько деталей в час делает первый рабочий, если известно, что второй за час делает на 1 деталь больше? • Второй этап. Работа с математической моделью. Решим уравнение: При данных значениях x знаменатели дробей не равны нулю, значит эти значения - корни составленного уравнения.

#18 слайд
На изготовление 40 деталей первый рабочий тратит на 2
часа больше, чем второй на изготовление 36 деталей.
Сколько деталей в час делает первый рабочий, если
известно, что второй за час делает на 1 деталь больше?
•
Третий этап. Ответ на вопрос задачи.
Так как производительность не может
выражаться отрицательным числом, то
значение не подходит условию задачи.
деталей в час делает первый рабочий.
Ответ: 5 деталей.
18 слайд
На изготовление 40 деталей первый рабочий тратит на 2 часа больше, чем второй на изготовление 36 деталей. Сколько деталей в час делает первый рабочий, если известно, что второй за час делает на 1 деталь больше? • Третий этап. Ответ на вопрос задачи. Так как производительность не может выражаться отрицательным числом, то значение не подходит условию задачи. деталей в час делает первый рабочий. Ответ: 5 деталей.

#19 слайд
Домашнее задание:
Составьте математические модели задач
1) С автобусной станции выехал автобус до железнодорожного вокзала,
находящемся на расстоянии 40 км. Один из пассажиров автобуса
опоздал к отправлению автобуса, и поехал на железнодорожный вокзал
на такси, через 10 минут после автобуса. Автобус и такси приехали на
железнодорожный вокзал одновременно. Известно также, что скорость
такси на 20 км/ч больше скорости автобуса. Необходимо найти скорость
такси и скорость автобуса.
S V t
автобус
такси
19 слайд
Домашнее задание: Составьте математические модели задач 1) С автобусной станции выехал автобус до железнодорожного вокзала, находящемся на расстоянии 40 км. Один из пассажиров автобуса опоздал к отправлению автобуса, и поехал на железнодорожный вокзал на такси, через 10 минут после автобуса. Автобус и такси приехали на железнодорожный вокзал одновременно. Известно также, что скорость такси на 20 км/ч больше скорости автобуса. Необходимо найти скорость такси и скорость автобуса. S V t автобус такси

#20 слайд
Составьте математические модели
задач
S V t
По течению
Против течения Домашнее задание:
2) Теплоход, собственная скорость которого 18 км/ч, прошел 50 км
по течению реки и 8 км против течения, затратив на весь путь
3 часа. Какова скорость течения реки?
20 слайд
Составьте математические модели задач S V t По течению Против течения Домашнее задание: 2) Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 часа. Какова скорость течения реки?

#21 слайд
Составьте математические модели задач
3) Секретарь хочет набрать на компьютере рукопись объемом 450
страниц. Если он будет набирать на 5 страниц в день больше,
чем запланировал, то закончит работу на 3 дня раньше. Сколько
страниц в день планирует набирать секретарь?
работа производительность время
По плану
Фактически Домашнее задание:
21 слайд
Составьте математические модели задач 3) Секретарь хочет набрать на компьютере рукопись объемом 450 страниц. Если он будет набирать на 5 страниц в день больше, чем запланировал, то закончит работу на 3 дня раньше. Сколько страниц в день планирует набирать секретарь? работа производительность время По плану Фактически Домашнее задание:

#22 слайд
Исторический материал
Уже около 4000 лет назад вавилоняне и
египтяне решали
разные задачи землемерия, строительства и
военного дела с
помощью уравнений. Уравнения первой и
второй степеней
умели решать в древности также китайские и
индийские ученые.
22 слайд
Исторический материал Уже около 4000 лет назад вавилоняне и египтяне решали разные задачи землемерия, строительства и военного дела с помощью уравнений. Уравнения первой и второй степеней умели решать в древности также китайские и индийские ученые.

#23 слайд
Задачи, решаемые с помощью уравнений,
встречаются во
многих текстах глубокой древности. В
Московском папирусе,
представляющем свиток, изготовленный из
растений, на
котором сделаны записи около 1850 г. до н. э. Исторический материал
23 слайд
Задачи, решаемые с помощью уравнений, встречаются во многих текстах глубокой древности. В Московском папирусе, представляющем свиток, изготовленный из растений, на котором сделаны записи около 1850 г. до н. э. Исторический материал

#24 слайд
В папирусе Ахмеса, например, содержатся
задачи, в которых неизвестное имеет особый
символ и название: «хау»
или «аха». Оно
означает
«количество», «куча».
Так называемое
«исчисление кучи» ,
или
«вычисление хау» , приблизительно
соответствует нашему решению задач с
помощью уравнений.Исторический материал
24 слайд
В папирусе Ахмеса, например, содержатся задачи, в которых неизвестное имеет особый символ и название: «хау» или «аха». Оно означает «количество», «куча». Так называемое «исчисление кучи» , или «вычисление хау» , приблизительно соответствует нашему решению задач с помощью уравнений.Исторический материал

#25 слайд
Пример решения задачи
Первый пешеход может пройти расстояния между двумя
пунктами на 5 часов быстрее, чем второй. Если они выйдут из этих
пунктов одновременно навстречу друг другу, то встретятся через 6
часов. За сколько часов каждый из них может пройти это
расстояние?
25 слайд
Пример решения задачи Первый пешеход может пройти расстояния между двумя пунктами на 5 часов быстрее, чем второй. Если они выйдут из этих пунктов одновременно навстречу друг другу, то встретятся через 6 часов. За сколько часов каждый из них может пройти это расстояние?

шағым қалдыра аласыз
















