Туынды көмегімен функцияны зерттеу және оның графигін салу

1 слайд
Туындының көмегімен Туындының көмегімен функцияны зерттеу функцияны зерттеу және және оның графигін салуоның графигін салу

1 слайд

2 слайд
Оку максаты 10.4.1.33 Туынды к ө мегімен функцияның касиеттерін зерттеу онын графигін салудың дағдысын калыптастыру

2 слайд

3 слайд
Сабақтың мақсаттары : • Функцияны туындының көмегімен зерттеу алгоритмімен танысу • Оны қолдану арқылы функцияны зерттеу • Графигін салуды үйрену

3 слайд

4 слайд
Естігенімді - ұмытамын. Көргенімді - есте сақтаймын. Жасағанымды - түсінемін. Конфуций

4 слайд

5 слайд
1. Суретте [-6;6]-де анықталған функциясының графигі кескінделген . у = f '(х) функциясы теріс болатын аралықтар санын көрсетіңдер. 4у = f ( x )

5 слайд

6 слайд
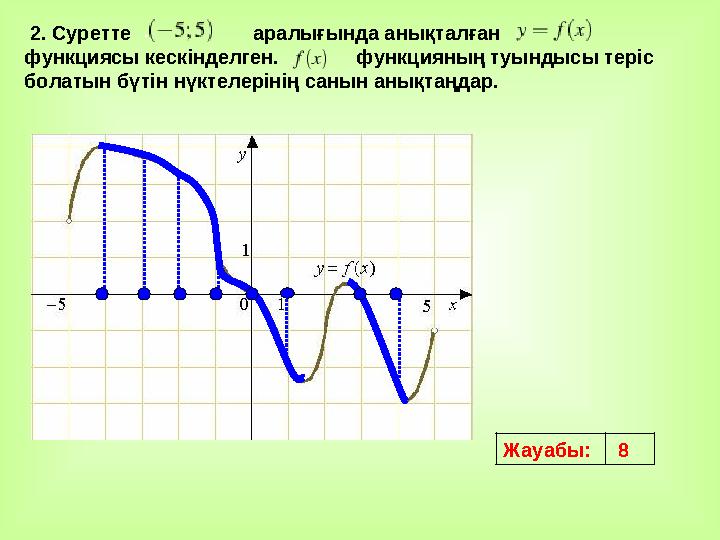
2. Суретте аралығында анықталған функциясы кескінделген. функцияның туындысы теріс болатын бүтін нүктелерінің санын анықтаңдар. Жауабы: 8

6 слайд

7 слайд
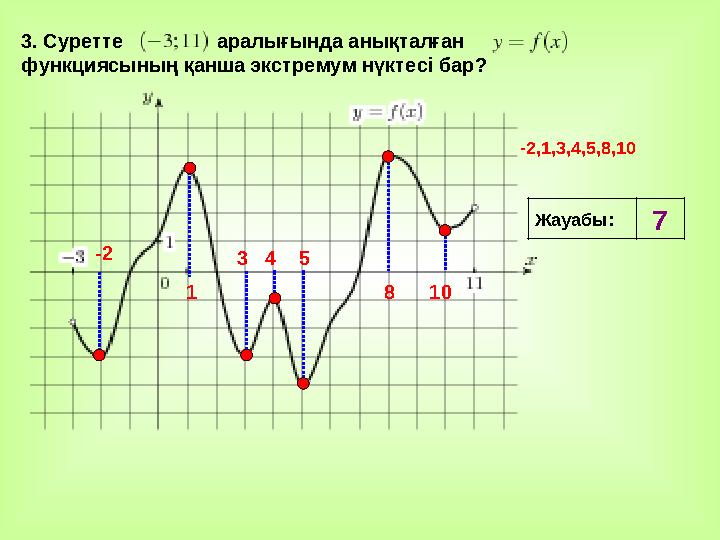
Жауабы: 73 . Суретте аралығында анықталған функциясының қанша экстремум нүкте c і бар? 3 .-2 1 4 5 8 10 -2,1,3,4,5,8,10

7 слайд

8 слайд
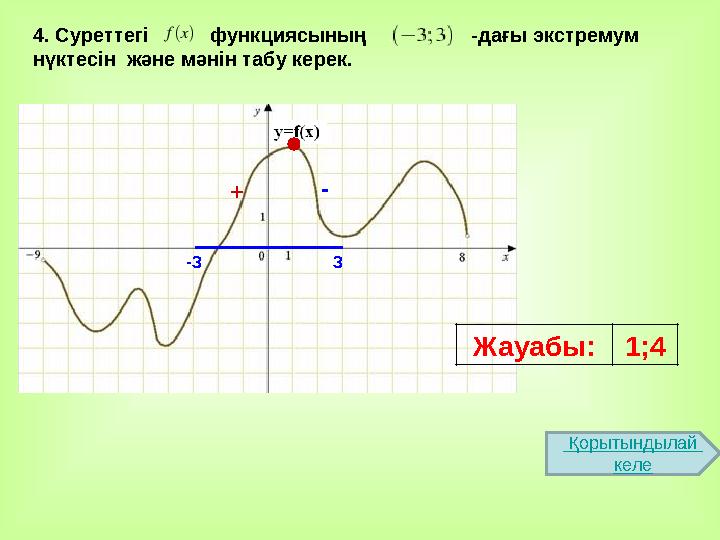
4 . Суретте гі функциясының -дағы экстремум нүктесін және мәнін табу керек. -3 3 Жауабы: 1;4+ - Қорытындылай келе

8 слайд

9 слайд
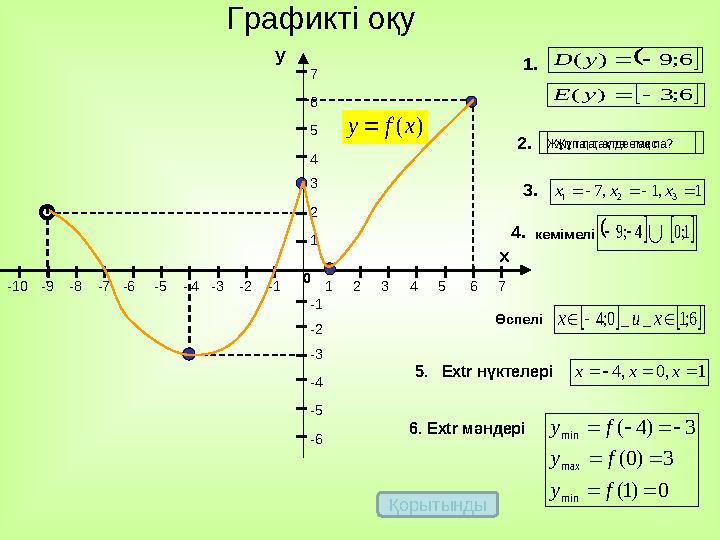
Графикті оқу) (x f y  0 1 52 3 4 76 ху 13 24567 -2 -1 -1 -2-3 -6-5 -5-4-3- 4-8 -7 -6-10 -9   6; 9 ) (   у D   6; 3 ) (   у Е Жұп па, әлде тақ па? 1 ,1 ,7 3 2 1      х х х кемімелі    6;1 _ _ 0;4    х и х Өспелі 0 )1( 3 ) 0( 3 ) 4 ( min max min         f y f y f у    1;0 4 ;9    1 ,0 ,4     х х х 1. 2 . 4 . 3 . 6 . Extr мәндері 5 . Extr нүктелері Жұп та, тақ та емес Қ орытынды

9 слайд

10 слайд
• Анықталу обл. (Анықталу обл. ( DD ) табу.) табу. • Жұп-тақтыққа зерттеу: Жұп-тақтыққа зерттеу: y(-x)=y(x) y(-x)=y(x) жұп (графигі Оу өсіне қар/да симм.)жұп (графигі Оу өсіне қар/да симм.) y(-x)=y(-x)= - - y(x) y(x) тақ (графигі О-коор.бас нүкт.қар/да тақ (графигі О-коор.бас нүкт.қар/да симм.)симм.) • Периодтылыққа зерттеу.Периодтылыққа зерттеу. • Ох, Оу өстерімен қиылысу нүктелерін табу:Ох, Оу өстерімен қиылысу нүктелерін табу: y=y= 00 (Ох өсімен қиылысу нүктесі) (Ох өсімен қиылысу нүктесі) , , x=x= 0 (Оу өсімен қиылысу нүктесі) 0 (Оу өсімен қиылысу нүктесі) • Таңба тұрақтылық аралықтарын табу:Таңба тұрақтылық аралықтарын табу: y>y> 00 (графиктің Ох өсінен жоғ. жатқан бөлігі)(графиктің Ох өсінен жоғ. жатқан бөлігі) , , y<y< 00 (графиктің Ох өсінен төм. жатқан бөлігі)(графиктің Ох өсінен төм. жатқан бөлігі) , , • Функция туындысын, өФункция туындысын, ө су,су, кему аралықтарын, экстремумдарын кему аралықтарын, экстремумдарын табу. табу. • Асимптоталарын табу:Асимптоталарын табу: а)а) верт.асимпт.: верт.асимпт.: хх =a -=a - түзуі, егертүзуі, егер б) көлбеу асимпт. б) көлбеу асимпт. -- тт үзуі, егер үзуі, егер Функцияның ойыс, дөңес аралыктарын, иілу нүктесін табуФункцияның ойыс, дөңес аралыктарын, иілу нүктесін табу • Кесте құру, графигін салуКесте құру, графигін салу) ( lim , lim kx y b x y k x х           ) ( lim x f а х b kx y  

10 слайд

11 слайд
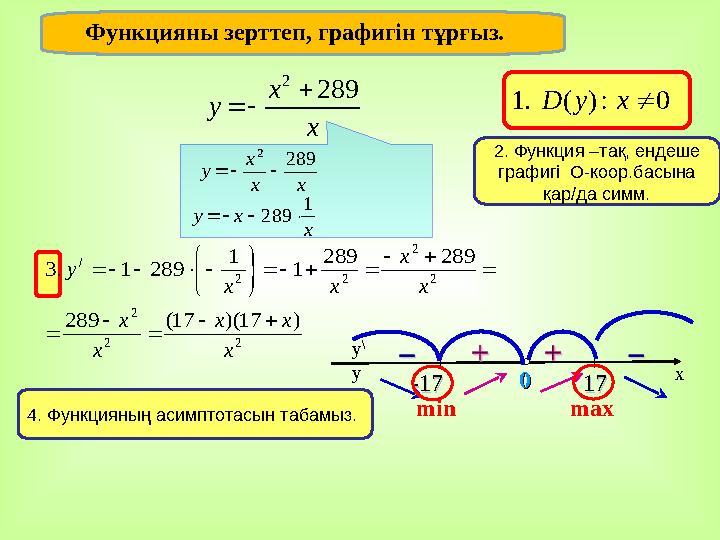
Функцияны зерттеп, графигін тұрғыз.0 : ) ( . 1  x y D х х y 289 2    2 2 2 2 2 2 2 / ) 17 )( 17( 289 289 289 1 1 289 1 . 3 х х х х х х х х х у                        х х y 1 289     х х х y 289 2    xy \ y 171700 -17-17 min max 2. Функция – тақ, ендеше графигі О - коор .басына қар/да симм. 4. Функцияның асимптотасын табамыз.

11 слайд

12 слайд
б) Көлбеу асимптота: y=k х +b түзуі, мұндағы k, b сандары келесі формулалардан табылады:, 0 289 289 2 lim 0               x x x4. Функцияның асимптоталарын табамыз. а) Вертикаль асимптота: х =0 түзуі (Оу өсі), себебі:               0 289 289 2 lim 0 x x x ы асимптотас колбеу -x у , 0 289 lim ) ) ( ( lim b ,1 289 lim ) ( lim 2 2 2                                   x x x kx x f x x x x f k х х х х x (-∞;-17) -17 (-17;0) 0 (0;17) 17 (0;+∞) f / ( x) - 0 + - + 0 - f ( x) 34 - -34 extr min - max

12 слайд

13 слайд
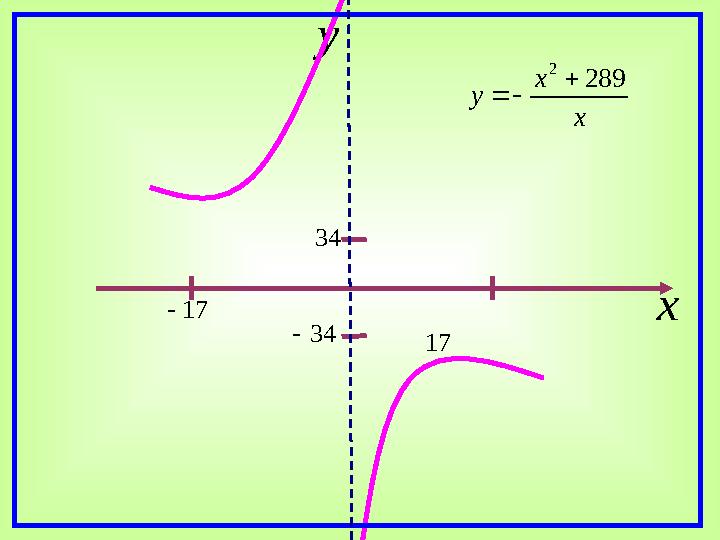
x y 17 34 34  17  x x y 289 2   

13 слайд

14 слайд
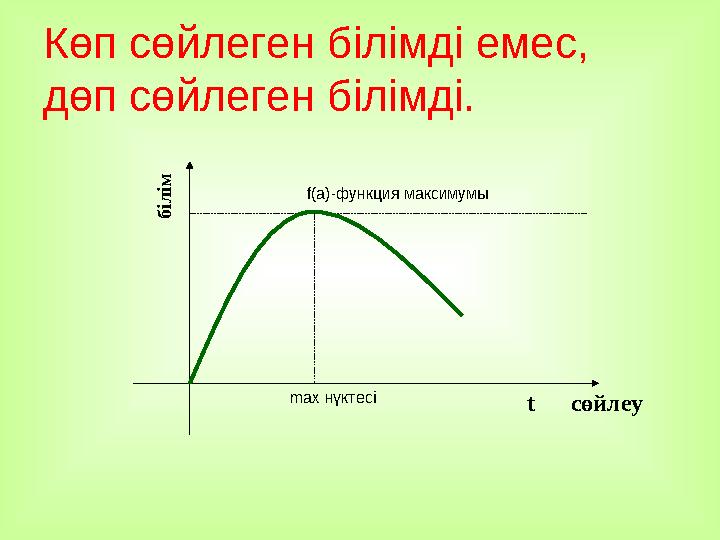
t c өйлеу Көп сөйлеген білімді емес, дөп сөйлеген білімді. max нүктесіf(a)- функци я максимумыб іл ім

14 слайд

15 слайд
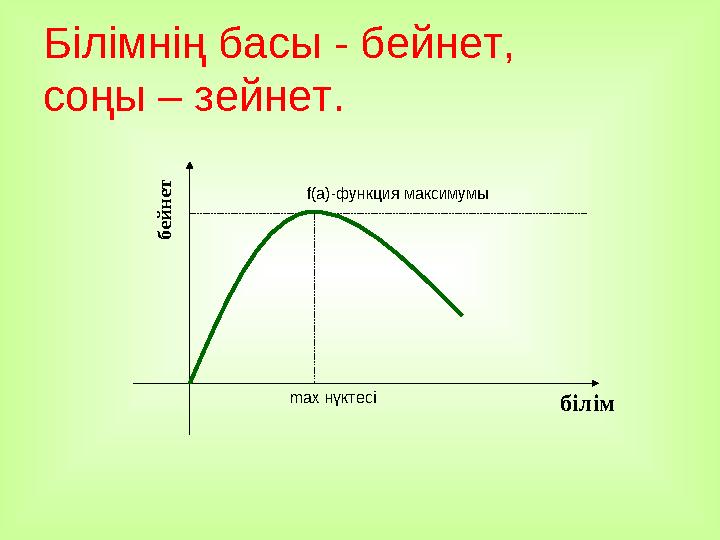
білімБілімнің басы - бейнет, соңы – зейнет. max нүктесіf(a)- функци я максимумыб ей н ет

15 слайд

16 слайд
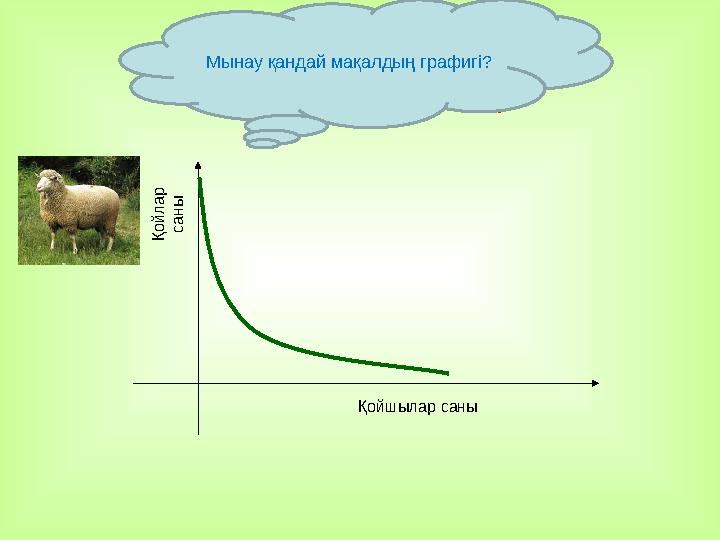
Қойшы көп болса, қой арам өледі Қойшылар саныҚойлар саныМынау қандай мақалдың графигі?

16 слайд

17 слайд
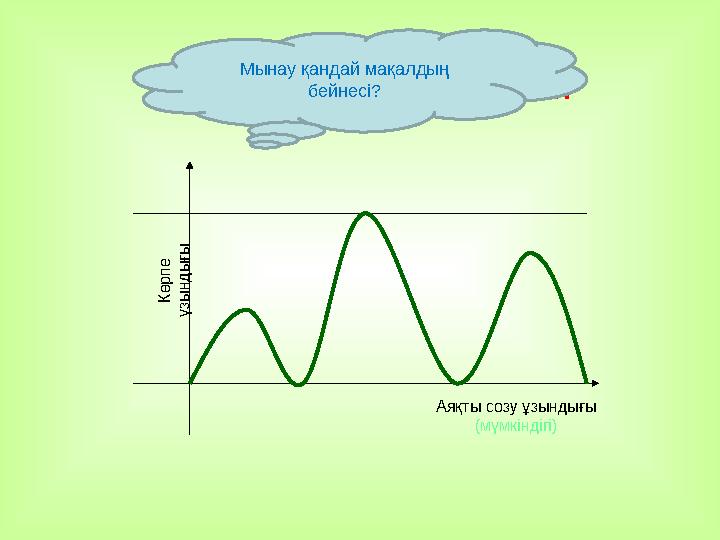
Көрпеңе қарай көсіл . Аяқты созу ұзындығы (мүмкіндігі) Көрпе ұзы нды ғыМынау қандай мақалдың бейнесі?

17 слайд

18 слайд
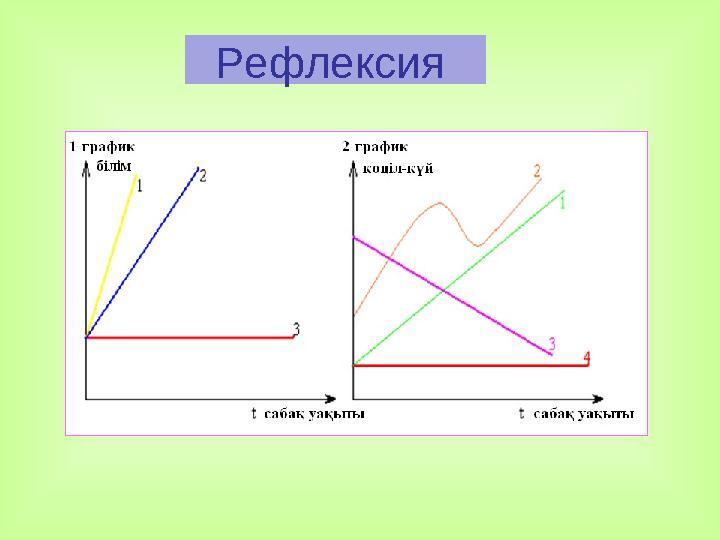
Рефлексия

18 слайд

19 слайд
Сабақтың қорытындысы: • «Бүгінгі сабақ … ұнады» • «Бүгінгі сабақта …білдім» • «Бүгінгі сабақта … үйрендім» • «Бүгінгі сабақта … таныстым» • «Бүгінгі сабақта … қайталадым» • «Бүгінгі сабақта … түсіндім» • «Бүгінгі сабақ … таңқалдырды»

19 слайд