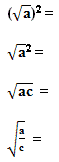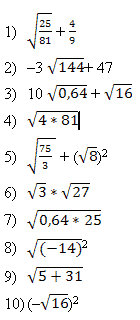Тип урока: изучение и первичное закрепление новых знаний.

Цель урока: сформулировать определение квадратного уравнения, научить учащихся решать уравнения вида х² = а, способствовать формированию получать информацию.

Оформление и оборудование:

компьютер,

мультимедиапроектор

карточки-задания для работы в парах

карточки с тестами для саморефлексии

презентация (Приложение).

ХОД УРОКА

1. Актуализация знаний

а) Устно:  вспомнить понятие арифметического квадратного корня, формулы

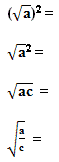
б) Применяя эти формулы,  решите примеры, и вы отгадаете имя известного математика и астронома IX века.

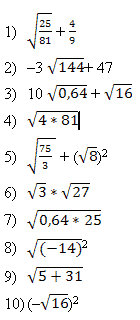
Ключ к решению: 1 – А,  2  – Д,  16 – И,  4 – Е,  5 – К,  6 – М,  8 – Н,  7 – П,  9 – Р, 10 – Т,  11 – Л,  12 – Ь,  13 – О, 14 – З, 18 – Х.

Решение: Аль-Хорезми. Приложение. Слайд 2.

2. А теперь небольшая историческая справка об этом человеке (рассказ ученика)

Аль-Хорезми (750 – 850). Полное имя – Абу Абдаллах Мухаммад ибн Муса ал Хорезми – один из крупнейших ученых (математик, астроном, историк, географ) средневековья. Приведенные годы жизни условны. Родина Аль-Хорезми – Хорезм, обширная область Средней Азии, которой соответствует теперешний Узбекистан. Он  известен тем, что написал основополагающий трактат по алгебре, который был посвящен решению уравнений и ученый рассматривал этот вопрос как самостоятельную науку. В книге Аль-Хорезми шла речь о двух важнейших операциях, необходимых при решении уравнений: переносе членов уравнения с одной стороны равенства в другую и о приведении подобных членов уравнения. От названия книги Ал-джабр  произошло слово «алгебра». В книге содержатся решения уравнений 1 и 2 степени. Аль-Хорезми приводил и геометрические способы решения уравнений. Его книга пользовалась большой популярностью, а в математике осталось и имя автора в латинизированном виде: алгоритм. Это слово теперь означает систему вычислений по определенным правилам. Аль-Хорезми впервые представил алгебру как науку об общих методах решения уравнений, дал их классификацию, что было очень существенно для «добуквенной»  алгебры.

Работа со слайдом 3. (Приложение)

2х = 8,
3х² = 6,
5х² – 7х = 0,
х² – 4х + 5 = 0,
3х – 6 = 5 + 4х.

Учитель: Какие уравнения относятся к уравнениям 1 и 2 степени? Учащиеся делают  сравнительный анализ уравнений 1 и 2 степени.
Учитель: Уравнения 1 степени вы уже решать умеете, а вот уравнения 2 степени еще нет. Теперь ваша очередь познакомиться с ними. Сформулируем теперь тему урока? Учащиеся дают варианты тем. Приложение. Слайд 4.

3. Изучение нового материала. Работа со слайдом 5 (Приложение)

Учитель: На слайде записаны вопросы, на которые, работая в парах,  вы должны найти ответ в учебнике.

Вопросы:

Какое уравнение называется квадратным?

Как называются числа а, b, с?

Приведите примеры квадратных уравнений.

Работа с классом.  Учащиеся отвечают на поставленные вопросы.

На слайде 6: Квадратным уравнением называется уравнение вида ах² + bх + с = 0, где а, b, с – заданные числа, х – неизвестное. (Записать определение в тетрадь)

На слайде 7:  ах² + bх + с = 0, а – старший коэффициент, b –  второй коэффициент, с – свободный член. (Записать в тетрадь)

Вопросы по слайду:

– Существенно ли  условие  а=/=0?
– Могут ли быть равными 0  другие коэффициенты?

Учащиеся анализируют.

Привести два-три примера квадратных уравнений на доске и в тетради

Работа со слайдом 8.  Из приведенных уравнений указать квадратные и назвать коэффициенты.

3х² + 4х – 7 = 0

– 2х² + 7х + 5 = 0

2х – 3 = 5

4х – 5х² = 1 = 0

6х – 3 = 5х + 5

– х² – х + 2 = 0

Работа со слайдом 9. С помощью указанных коэффициентов составить квадратное уравнение.

1) а = 6, b = 7, с = – 1.
2) а = – 1, b = – 1, с = 3
3) а = 4, b = 6, с = – 2.

Работа со слайдом 10. Проверить полученные уравнения.

1) 6х² + 7х – 1 = 0
2) – х² – х + 3 = 0
3) 4х² + 6х – 2 = 0

Учитель: Разделите тетрадь на 3 части и решите 3 уравнения. Что значит решить уравнения? (Найти корни, или доказать что их нет). Что значит найти корни? (Найти значение переменной, при которой выполняется верное равенство). Являются ли данные уравнения квадратными?

х² = 81                   х² = 0               х² = – 81
х = 9, х = – 9          х = 0               корней нет.

Учитель. Если рассмотреть уравнение в общем виде х² = а, то от чего будет зависеть его решение? (От а)

Попробуем сделать вывод:

Если а > 0, то уравнение имеет 2 корня х₁ = 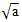 , х₂ =  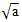–  . (Привести пример решения геометрической задачи на применение теоремы Пифагора.  Почему в ответе записываем только один корень?)
Если а = 0, то уравнение имеет один корень, х = 0.
Если а < 0, то корней нет.

Приложение. Слайд 11. Записать в тетрадь.

4. Первичное закрепление. Работа с учебником

№ 407 (устно)
№ 408 (1, 3, 5) – самостоятельно
№ 409 (1, 3, 5) показать на доске.

5. Рефлексия. Решение теста с выбором ответа (проверить в парах)

Тест:

1. х² = 121

а) х = 11
б) х = –11
в) х = ±11

2. х² – 144 = 0

а) х =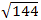 
б) х = ± 12      
в) корней нет

3. х² = – 9

а) х= ± 3
б) х = – 3
в) корней нет

4. х² = 0

а) х = 0
б) х =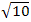 
в) корней нет

5. х² + 4 = 0

а) корней нет
б) х = 2
в) х = ±2

6. Подведение итога урока. Домашнее задание

.№ 408 (2, 4, 6), № 409 (2, 4, 6), № 410 (2, 4) – группа А.