Доклад на тему "Геометрическое определение комфортности жилья"

ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КОМФОРТНОСТИ ЖИЛЬЯ

Нуруллаев Максадбек Эльмуратович

Туркестанский индустриально-строительный колледж

студент группы 21-09

«Все вокруг геометрия!»
Ле Корбюзье

Вся жизнь современного человека проходит в тесной связи с математикой. Современная жизнь людей на столько сложна и многообразна, что им постоянно приходиться совершенствовать свою математическую культуру и постоянно при решении насущных проблем обращаться к математике. Куда бы ни кинул взгляд человек – всюду геометрические объекты, всюду геометрия. К тому же место, где человек проводит большую часть своей жизни, его жилище, тоже имеет определенную геометрическую форму.А каким должен быть дом современного человека? При строительстве любого дома люди всегда задаются вопросом: «Какой дом лучше?». «Лучше тот, что теплее» – скажут одни, «лучше тот, что красивее или комфортнее» - скажут другие. Но есть ли способ определить – это «лучше»? Попробуем ответить на этот вопрос с точки зрения геометрии.В последнее время все чаще говорят о том, что мировые запасы природных ресурсов небезграничные, остро стоит проблема энергосбережения. Одним из способов сэкономить тепло является обеспечение жилья наименьшей потерей тепла через его поверхность. Можно существенно уменьшить размеры дома, но человек должен иметь достаточно жилого пространства, чтобы чувствовать себя комфортно. Таким образом, встает вопрос: как достичь сочетания максимально возможного объема жилого пространства при минимальной площади поверхности, через которую может уходить тепло. И сейчас этот вопрос остается для человечества особенно актуальным.В связи с этим была поставлена цель исследования: выяснить, дом какой формы наиболее комфортен для проживания с точки зрения соотношения объема жилья и его поверхности.

Что определило задачи исследования:

1. Выбрать для исследования несколько видов жилищ разных геометрических форм и размеров.

2. Определить формулы вычисления объемов и площадей поверхности различных геометрических тел, соответствующих выбранным жилищам.

3. Вычислить коэффициенты комфортности для каждого жилища.

4. Выявить жилище наиболее комфортной для проживания формы с точки зрения соотношения объема жилищного пространства и его поверхности.

Объект исследования: использование геометрии в жизни человека.

Предмет исследования: применение геометрии для определения коэффициента комфортности жилья.

Гипотеза исследования: существует жилище определенной геометрической формы, имеющее наибольший коэффициент комфортности для жизни человека.

Методы исследования:

1. наблюдение;

2. поиск и отбор информации;

3. анализ, исследование, систематизация материала.

Применение геометрии в строительстве

Профессия строителя является очень древней. До наших дней дошло немало сооружений, возраст которых измеряется тысячелетиями. Свой опыт мастера строительного дела передавали из поколения в поколение, в том числе и математические знания. В строительстве никак не обойтись без математики. В современном строительстве роль этой науки непрерывно возрастает. Специалисты должны создавать и перерабатывать чертежи, тексты, документы, таблицы, формулы; выполнять расчеты площадей различных фигур, объёмов многогранников и тел вращения. Важно отметить и обратную историческую взаимосвязь: потребности зарождающегося строительства и, возникшей вслед за ним архитектуры, явились одним из стимулов, благодаря которым возникла и сделала первыешаги геометрия. Ни один из видов искусств так тесно не связан с геометрией как архитектура и строительство. Тесная связь геометрии и архитектуры известна с давних времен. Издревле геометрия считалась одним из разделов архитектуры.Архитекторы утверждают, что геометрия – это основа архитектурного мастерства. С давних времен люди возводя свои жилища думали об их прочности, удобстве, внешнем виде, устойчивости к погодным и климатическим условиям. Прочность сооружения заключается не только в материале, из которого оно сделано, но и в конструкции, используемой при строительстве.Архитектурные произведения живут в пространстве, являются его частью, вписываясь в определенные геометрические формы. Кроме того, они состоят из отдельных деталей, каждая из которых также строится на базе определенного геометрического тела. Часто геометрические формы сооружений являются комбинациями различных геометрических тел.

Геометрические фигуры и тела в строительстве

Куб - правильный многогранник, каждая грань которого представляет собой квадрат.Призма - многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани -параллелограммами.Пирамида - многогранник, основание которого - многоугольник, а остальные грани - треугольники, имеющие общую вершину.Сфера (от греческого - мяч, шар) - это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).Конус - тело, ограниченное конической поверхностью и кругом основания.Цилиндр - геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Объемы тел и площади поверхностей

Для измерения объемов и площадей поверхности многогранников и тел вращения используются следующие формулы.

Куб: S_(п.п.)=6а^2 ,V=а^3

Призма: S_(п.п.)=2S_o+S_(б.п.) ,S_(б.п.)=P_(o )∙H ,V=S_o∙H

Пирамида: S_(п.п.)=S_o+S_(б.п.) ,S_(б.п.)=1/2 P_(o )∙d ,V=1/3 S_o∙H

Сфера, шар: S_(п.п.)=4∙π∙R^2 ,V=4/3 (∙π∙R)^3

Конус: S_(п.п.)=S_o+S_(б.п.) S_(б.п.)=π∙R∙l ,V=1/3 (∙π∙R)^2∙H

Цилиндр: S_(п.п.)=2S_o+S_(б.п.),S_(п.п.)=2∙π∙R∙H ,V=(π∙R)^2∙H

Вычисление коэффициента комфортности жилья разной геометрической формы

Жилище – место жизни человека, место, где он рождается, растет. Это кров, укрытие, место покоя и порядка. Жилище как центр человеческой вселенной осознается почти повсеместно. Но в зависимости от образа жизни и места на земном шаре оно имеет большую или меньшую значимость для человека. Вместе с этим каждый человек стремится к более высокому качеству жизни, которое зависит от комфортности условий, обеспечивающих жизнедеятельность человека. Существует зависимость между комфортом нашего дома и его математическими характеристиками: например, объёмом и площадью. Ученые предложили формулу вычисления комфортности жилища: . Здесь V – объём жилища (например, вашей комнаты) и S – полная поверхность жилища. Самым комфортным считается жильё с коэффициентом k = 1.Геометрия архитектуры окружающих нас зданий разнообразна. Как известно, разные народы строили для себя жилье разных форм, видимо, строители руководствовались известными им принципами. И почему кот, когда в холодную ночь он приготовляется ко сну, поджимает лапы, свертывается и таким образом делает свое тело насколько возможно шарообразным? Почему так удобно свернуться «калачиком», когда спишь? Видимо, соотношения формы, объема и площади поверхности тел имеют закономерность, влияющую на степень комфортности. Это можно доказать опытным путем. Вычислим коэффициент комфортности жилья разной геометрической формы.

1. Подавляющее число жилых зданий имеет форму куба или прямоугольного параллелепипеда.

Дано: куб с ребром а.

Найти: коэффициент комфортности к

Решение:1)Найдем объем куба: V=a³

2)Найдем площадь полной поверхности: Sп.п.=6а²

3)Найдем коэффициент комфортности к=(36π(а^3 )^2)/(〖6а〗^2 )^3 = (36πа^6)/(216а^6 )=π/6 к=0,52< 1 => жилье формы куба не очень комфортное!

Дано: жилище формы прямоугольного параллелепипеда с измерениями а=8м, b=4м, с=4м.

Найти: коэффициент комфортности к

Решение:

1) Найдем объем прямоугольного параллелепипеда: V= abc =128м³

2) Найдем площадь полной поверхности: Sп.п.=2(ab+bc+ac)=160 м²

3) Найдем коэффициент комфортности к <1, => жилье формы прямоугольного параллелепипеда не очень комфортное!

2. В современном мире существуют здания пирамидальной формы. Причины, по которым человечество древнего мира выбрало для строительства первых высотных зданий форму пирамиды, очевидны. Причина номер один: форму пирамиды подсказала сама природа. Причина номер два: форма пирамиды в строительстве при определенных условиях является самым надежным и крепким сооружением.

Дано: правильная четырехугольная пирамида, а=5 м, H=4 м

Найти: коэффициент комфортности к

Решение:

1. Найдем площадь основания: Sосн.= а2 =25м²

2. Найдем площадь боковой поверхности: Sб.п.= м²

3. Найдем площадь полной поверхности: Sп.п.= Sосн.+ Sб.п =72 м²

4. Найдем объём: V= а2 h =33(3)м³

5. Найдем коэффициент комфортности:

<1, => коэффициент далек от 1, жилье не комфортное!

3. Чум является универсальным жилищем северных народов. Это переносная конусообразная палатка, форма которой является приспособленной, целесообразной для тундры. Форма конуса делает жилище устойчивым при метелях и сильных ветрах, снег с него легко скатывается. Интересно, как чувствует себя человек в доме конусообразной формы с точки зрения комфортности.

Дано: жилище конусообразной формы h=4м, r =3м.

Найти: коэффициент комфортности к

Решение:

1) Найдем объем конуса: V=П r2 h =37,68м³

2) Найдем площадь полной поверхности: Sп.п.= П r2 + П rl =75,36 м²

3) Найдем коэффициент комфортности

К <1, => коэффициент далек от 1, жилье не комфортное!

4. Достаточно знаменит дом Константина Мельникова в Москве - шедевр русского авангарда, входящий во все учебники по архитектуре 20 века. Выбор цилиндрической формы архитектор объяснял тем, что в таком пространстве при отсутствии прямых углов полезная площадь намного больше, чем в традиционных зданиях.

Не менее известен «AquaDom» – это 25-метровый аквариум цилиндрической формы из акрилового стекла, построенный вокруг прозрачного лифта. Он находится в отеле «Radisson SAS Hotel» в Берлине. Есть такие дома и в Нур-Султане. Вычислим коэффициент комфортности проживания в цилиндрическом доме.

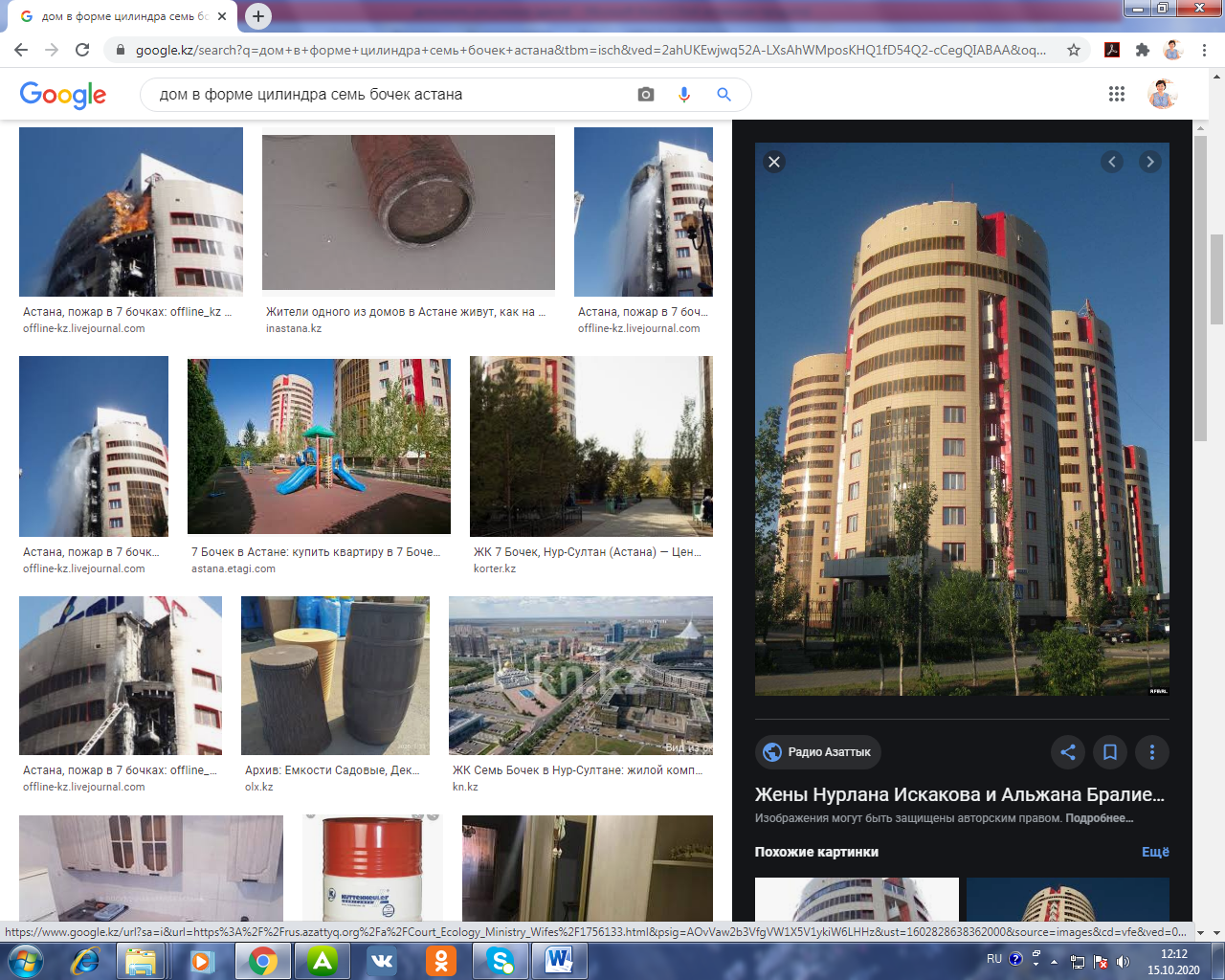
Дано: цилиндр, h=3м, R=2м.

Найти: коэффициент комфортности

Решение: Sполн.п. =2ПR(R+Н)=2·П·2(2+3)=20П≈62,8 м2

V= Sосн. · h =ПR²· h=12П≈37,68 м3

<1, тем не менее, пока это наибольший из полученных коэффициентов.

5. Рассмотрим несколько примеров вычисления коэффициентов комфортности комбинированного жилья. Жилье – прямоугольный параллелепипед + усеченная пирамида;

Дано: а=6м, в=4м, с=8м, а1= 3м, в1=2, h=3.

Найти: коэффициент комфортности к

Решение:

Найдём объём и площадь поверхности параллелепипеда:

V1=abc=192м², S1=6·4+6·8·2+8·4·2=184м²

Найдём объём и площадь полной поверхности усечённой пирамиды

V1 =h*(S+s+√Ss)/3=42м³

Sповерх=Sбок+Sосн =55,2

Найдём объём и полную поверхность комбинации тел

V=V1+V2= 234,2 м², S =239,2м², К=36πv2 \S³=0,45<1

Коэффициент комфортности низкий, жилье не комфортно.

Жилье – полусфера + цилиндр.

Дано: R=2, h=5.

Найти: коэффициент комфортности к

Решение: Vцилиндра = ПR2h=251,2 м3,

Vполушара = ПR3=133,973 м3, Vтела=385,17 м3.

Sцилиндра = 2ПRh+ ПR2=175,84 м2, Sполусферы = 4ПR2=100,48 м2, Sтела=276,32 м2 К=36πv2\S³=0,7949 < 1

Это наибольший из полученных коэффициентов.

6. Современное строительство предлагает дома сферической формы. Как один из примеров такого здания – это здание ЭКСПО в Нур-Султане.

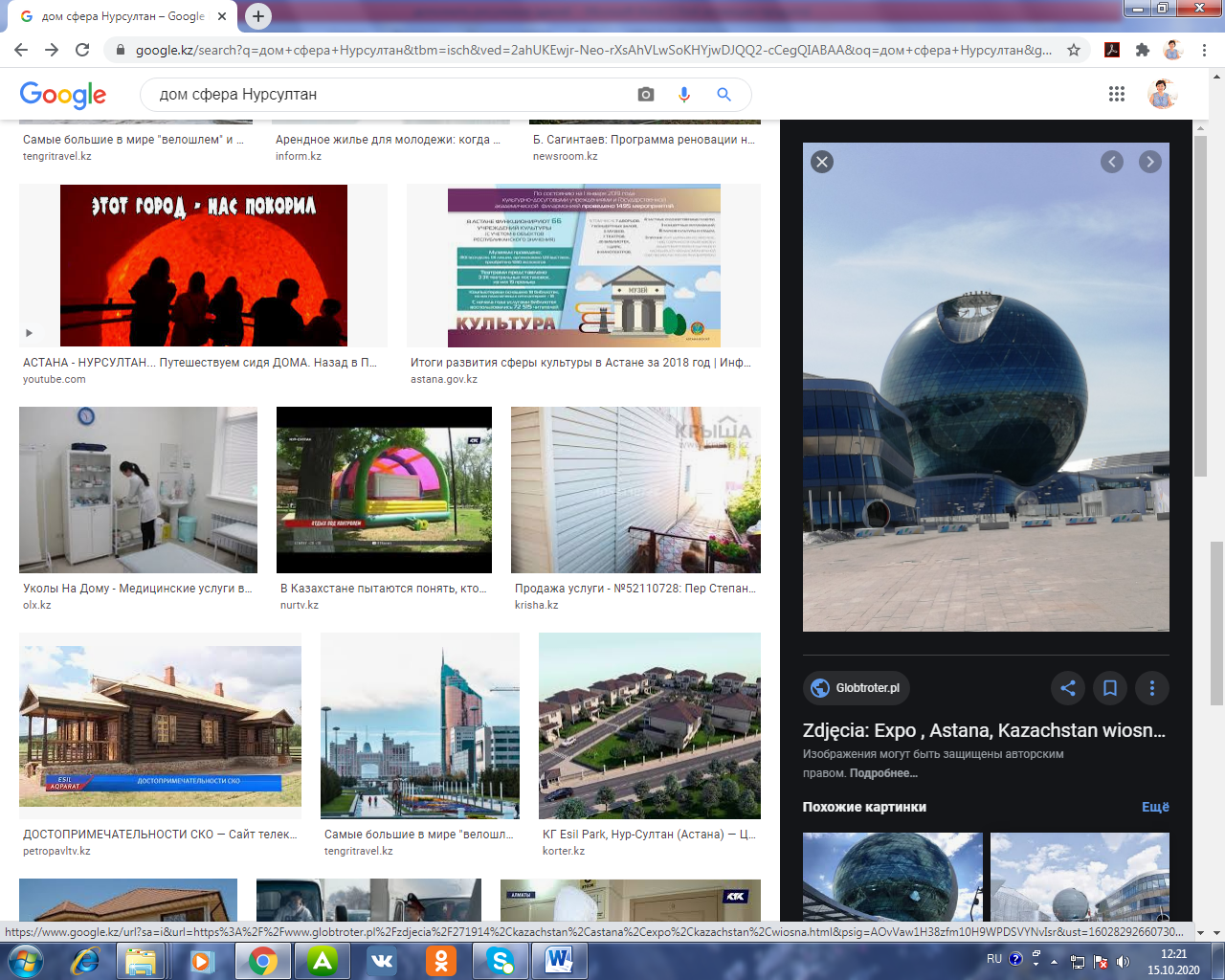
Дано: жилье шарообразной формы радиусом R.

Найти: коэффициент комфортности

Решение: Sсферы.=4 πR2, V=(4πR^3)/3,

С помощью математических расчетов получены следующие результаты комфортности жилья таблица 1. Это самый высокий результат!

№п/п	Вид жилья	Коэффициент комфортности, к
1	Куб	0,52
2	Прямоугольный параллелепипед	0,45216
3	Пирамида	0,335
4	Конус	0,375 770 ₸ - Сатып алу Материал ұнаса әріптестеріңізбен бөлісіңіз Ватсапта бөлісу Телеграммда бөлісу Фейсбукта бөлісу Сілтемені көшіру Ашық сабақ, ҚМЖ, көрнекілік, презентация жариялап табыс табыңыз! Материалдарыңызды сатып, ақша табыңыз. (kaspi Gold, Halyk bank) Соңғы бір жылда: 45 000 000 ₸ Авторлар тапқан ақша Толығырақ Ресми байқаулар тізімі Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз! Тізімді көру Материал іздеу Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде пәніңізді белгілеп, керек материалды алып сабағыңызға қолдана аласыз Барлығы 663 959 материал жиналған Пән Жүктелуде... Бағыт Жүктелуде... Сынып Жүктелуде... Іздеу Ұқсас материалдар Дайын ҚМЖ. Барлық пәндерден 2024-2025 оқу жылына, жаңа бұйрыққа сай жасалған Сертификатталған тренер жасаған 01.01.2023 17 863 13 694 ҚР Білім және Ғылым министірлігінің стандарты бойынша жасалған. Барлық пәндер Барлық материалдар Барлық сыныптар Геометрия пәні бойынша барлық материалдарды көру Аттестацияда (ПББ) 100% келетін тақырыптармен дайындаймыз Аттестацияда (ПББ) келетін тақырыптар бойынша жасалған тесттермен дайындалып, бізбен бірге тестілеуден оңай өтесіз Өткен жылы бізбен дайындалған ұстаздар 50/50 жинап рекорд жасады Толығырақ