Тригонометриялық функциялар
Тригонометрия (грек. trіgōnon – үшбұрыш және metreo – өлшеу) – геометрияның үшбұрыш элементтерінің арасындағы метрикалық қатыс тригонометриялық функциялар арқылы өрнектелетін саласы. Тригонометрияның негізгі мәселесі үшбұрыштың белгісіз шамаларын берілген шамалар арқылы есептеу болып табылады. Тригонометрия жазық, түзу сызықты және сфералық тригонометрия болып бөлінеді.
![]() Мазмұны
Мазмұны
Тарихы
Евклидтік кеңістіктің сфералары қарастырылатын тригонометрия сфералық тригонометрия деп аталады. Жазық тригонометрия сфералық тригонометриядан кейінірек дами бастады. Мысалы, Евклидтің «Негіздерінің» 2-кітабында косинустар теоремасы жайында айтылған. Тригонометрияны әл-Баттани (9–10 ғасырлар), Әбу-л-Вефа (10 ғасыр), Бхаскара (10 ғасыр) және ат-Туси (13 ғасыр), т.б. одан әрі дамытты. Оларға синустар теоремасы белгілі болған. Тангенстер теоремасын Региомонтан (15 ғасыр) тапқан. Одан кейін тригонометрияны дамытуға Н.Коперник (16 ғасырдың 1-жартысы), Т.Браге (16 ғасырдың 2-жартысы), Ф.Виет (16 ғасыр), И.Кеплер (16–17 ғасырлар), т.б. үлес қосты. Қазіргі түріндегі Т. Л.Эйлердің еңбектерінде баяндалды.
Тригонометрия ғылыми термин ретінде адамның практикалық әрекеттерінің нәтижесінде пайда болды. Ерте кезде астрономия ғылымы, суда жүзу, жер өлшеу, архитектура талаптары қандай да бір элементтер арқылы есептеу әдістерін ойлап табуға әкелді. Мысалы, олардың көмегімен қол жетпейтін заттарға дейінгі қашықтықты анықтау және географиялық карталарды құрастыруға арналған жергілікті жердің геодезиялық көшірмесін жасау жұмыстары бірқатар оңайлатылды. Мектепте тригонометриялық материалмен алғаш рет планиметрия курсын оқығанда танысады. Тригонометрияның көмегімен жазық үшбұрыштарды шығарды. Тригонометриялық қатынастар «синус», «тангенс» деген атқа ие болды, олардың мәндері есептеліп шығарылды. Тригонометриялық танымдардың негізі ежелгі заманда пайда болды. Аталмасы біршама кейінірек шыққанымен, тригонометрияға қатысты қазіргі көптеген ұғымдар мен фактілер бұдан екі мың жыл бұрын белгілі болған. Кейбір тригонометриялық мәліметтер ежелгі вавилондықтар мен египеттіктерге белгілі болған, бірақ ғылым ретінде Ежелгі Грецияда негізделген. Тригонометрия сөзі алғаш рет 1505 жылы неміс геологы және математигі Питискустың кітабының мазмұнында кездеседі. «Тригонометрия» атауының өзі грек сөзінен аударғанда «үшбұрыштарды өлшеу» деген ұғымды білдіреді. Ежелгі грек ғалымы белгілі астроном Клавдий Птолемей (ІІ ғ) «хорда тригонометриясын» ойлап тапты. Дайын кестелермен жұмыс істегенде немесе калькуляторды пайдаланғанда, біз көбінесе кестелер әлі ойлап табылмаған кездердің де болғанын естен шығарып аламыз. Оларды құру үшін аса көлемді есептеулерді орындап қана қоймай, кестелерді құрудың тәсілдерін де ойлап табу қажет болды. Птолемей кестесі бес ондық үлес таңбаларын қоса алғандағы дәлдікпен жасалған. Хордаларды синустармен ауыстырып, тригонометрияның әрі қарай дамуына үндістандық ғалымдар үлкен үлес қосты. Бұл жаңа енгізіу VIII ғасырда тригонометрияны бірте-бірте астрономия тарауынан бөліп алып, жеке ғылымға айналдырды. Ол араб тіліндегі жақын және алыс Батыс мемлекеттерінің математикасына ауысты. Оған үлес қосқандар Аль-хорезми, Аль-Коши, Насриддин Тусси, Жан фурье, Иоганн Бернули, Леонард Эйлер. Л.Эйлер тригонометрияның қазіргі кездегі түріне келтірілген XVIII ғасырдың ірі математигі еді, ол негізі швейцарлық, ұзақ жылдар бойы Россияда жұмыс істеген және Санкт-Петербург ғылым академиясының мүшесі болған. Тригонометриялық функциялардың белгілі анықтамасын да енгізген Л.Эйлер, кез келген бұрыштың функциясын қарастырып, келтіру формулаларын шығарып алды. Осылайша тригонометрия туралы жалпы ұғымдар, тригонометриялық функциялардың белгілеулері және анықтамалары ұзақ тарихи даму процесінде қалыптасып отыр.
Кейбір тригонометриялық функциялар
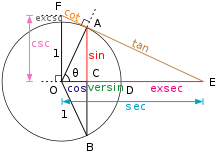
Бірлік шеңбердегі Ө бұрышына қатысты тригонометриялық функциялар.
Бастапқы кезден тригонометриялық функциялар тік бұрышты үшбұрыштағы қабырғаларының қатынастарымен байланыста болғаны белгілі. Олардың жалғыз аргументі сол үшбұрыштың бір сүйір бұрышы болып табылады.
-
Синус — қарама-қарсы жатқан катеттің гипотенузаға қатынасы.
-
Косинус — жанама катеттің гипотенузаға қатынасы.
-
Тангенс — қарама-қарсы жатқан катеттің жанама катетке қатынасы.
-
Котангенс — жанама катеттің қарама-қарсы жатқан катетке қатынасы.
-
Секанс — гипотенузаның жанама катетке қатынасы.
-
Косеканс — гипотенузаның қарама-қарсы жатқан катетке қатынасы.
Берілген анықтамалар функциялардың
сүйір бұрыштарға (0-ден π 2 {\displaystyle
\pi \over 2} ![]() радиан) қатысты мəндерін есептеуге
арналған.
радиан) қатысты мəндерін есептеуге
арналған.
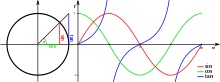
Тригонометриялық функциялардың графиктері.
Бірлік шеңбердегі Ө бұрышына қатысты тригонометриялық функцияларды қарастырсақ (суретті қара):
-
θ {\displaystyle \theta }
 бұрышының Синусы "A"
нүктесінің ординатасы ретінде анықталады.
бұрышының Синусы "A"
нүктесінің ординатасы ретінде анықталады. -
Косинус — "A" нүктесінің абсциссасы.
-
Котангенс — косинустың синусқа қатынасы.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Ғылыми жұмыс атауы: Тригонометриялық функциялар
Ғылыми жұмыс атауы: Тригонометриялық функциялар
Тригонометриялық функциялар
Тригонометрия (грек. trіgōnon – үшбұрыш және metreo – өлшеу) – геометрияның үшбұрыш элементтерінің арасындағы метрикалық қатыс тригонометриялық функциялар арқылы өрнектелетін саласы. Тригонометрияның негізгі мәселесі үшбұрыштың белгісіз шамаларын берілген шамалар арқылы есептеу болып табылады. Тригонометрия жазық, түзу сызықты және сфералық тригонометрия болып бөлінеді.
![]() Мазмұны
Мазмұны
Тарихы
Евклидтік кеңістіктің сфералары қарастырылатын тригонометрия сфералық тригонометрия деп аталады. Жазық тригонометрия сфералық тригонометриядан кейінірек дами бастады. Мысалы, Евклидтің «Негіздерінің» 2-кітабында косинустар теоремасы жайында айтылған. Тригонометрияны әл-Баттани (9–10 ғасырлар), Әбу-л-Вефа (10 ғасыр), Бхаскара (10 ғасыр) және ат-Туси (13 ғасыр), т.б. одан әрі дамытты. Оларға синустар теоремасы белгілі болған. Тангенстер теоремасын Региомонтан (15 ғасыр) тапқан. Одан кейін тригонометрияны дамытуға Н.Коперник (16 ғасырдың 1-жартысы), Т.Браге (16 ғасырдың 2-жартысы), Ф.Виет (16 ғасыр), И.Кеплер (16–17 ғасырлар), т.б. үлес қосты. Қазіргі түріндегі Т. Л.Эйлердің еңбектерінде баяндалды.
Тригонометрия ғылыми термин ретінде адамның практикалық әрекеттерінің нәтижесінде пайда болды. Ерте кезде астрономия ғылымы, суда жүзу, жер өлшеу, архитектура талаптары қандай да бір элементтер арқылы есептеу әдістерін ойлап табуға әкелді. Мысалы, олардың көмегімен қол жетпейтін заттарға дейінгі қашықтықты анықтау және географиялық карталарды құрастыруға арналған жергілікті жердің геодезиялық көшірмесін жасау жұмыстары бірқатар оңайлатылды. Мектепте тригонометриялық материалмен алғаш рет планиметрия курсын оқығанда танысады. Тригонометрияның көмегімен жазық үшбұрыштарды шығарды. Тригонометриялық қатынастар «синус», «тангенс» деген атқа ие болды, олардың мәндері есептеліп шығарылды. Тригонометриялық танымдардың негізі ежелгі заманда пайда болды. Аталмасы біршама кейінірек шыққанымен, тригонометрияға қатысты қазіргі көптеген ұғымдар мен фактілер бұдан екі мың жыл бұрын белгілі болған. Кейбір тригонометриялық мәліметтер ежелгі вавилондықтар мен египеттіктерге белгілі болған, бірақ ғылым ретінде Ежелгі Грецияда негізделген. Тригонометрия сөзі алғаш рет 1505 жылы неміс геологы және математигі Питискустың кітабының мазмұнында кездеседі. «Тригонометрия» атауының өзі грек сөзінен аударғанда «үшбұрыштарды өлшеу» деген ұғымды білдіреді. Ежелгі грек ғалымы белгілі астроном Клавдий Птолемей (ІІ ғ) «хорда тригонометриясын» ойлап тапты. Дайын кестелермен жұмыс істегенде немесе калькуляторды пайдаланғанда, біз көбінесе кестелер әлі ойлап табылмаған кездердің де болғанын естен шығарып аламыз. Оларды құру үшін аса көлемді есептеулерді орындап қана қоймай, кестелерді құрудың тәсілдерін де ойлап табу қажет болды. Птолемей кестесі бес ондық үлес таңбаларын қоса алғандағы дәлдікпен жасалған. Хордаларды синустармен ауыстырып, тригонометрияның әрі қарай дамуына үндістандық ғалымдар үлкен үлес қосты. Бұл жаңа енгізіу VIII ғасырда тригонометрияны бірте-бірте астрономия тарауынан бөліп алып, жеке ғылымға айналдырды. Ол араб тіліндегі жақын және алыс Батыс мемлекеттерінің математикасына ауысты. Оған үлес қосқандар Аль-хорезми, Аль-Коши, Насриддин Тусси, Жан фурье, Иоганн Бернули, Леонард Эйлер. Л.Эйлер тригонометрияның қазіргі кездегі түріне келтірілген XVIII ғасырдың ірі математигі еді, ол негізі швейцарлық, ұзақ жылдар бойы Россияда жұмыс істеген және Санкт-Петербург ғылым академиясының мүшесі болған. Тригонометриялық функциялардың белгілі анықтамасын да енгізген Л.Эйлер, кез келген бұрыштың функциясын қарастырып, келтіру формулаларын шығарып алды. Осылайша тригонометрия туралы жалпы ұғымдар, тригонометриялық функциялардың белгілеулері және анықтамалары ұзақ тарихи даму процесінде қалыптасып отыр.
Кейбір тригонометриялық функциялар
Бірлік шеңбердегі Ө бұрышына қатысты тригонометриялық функциялар.
Бастапқы кезден тригонометриялық функциялар тік бұрышты үшбұрыштағы қабырғаларының қатынастарымен байланыста болғаны белгілі. Олардың жалғыз аргументі сол үшбұрыштың бір сүйір бұрышы болып табылады.
-
Синус — қарама-қарсы жатқан катеттің гипотенузаға қатынасы.
-
Косинус — жанама катеттің гипотенузаға қатынасы.
-
Тангенс — қарама-қарсы жатқан катеттің жанама катетке қатынасы.
-
Котангенс — жанама катеттің қарама-қарсы жатқан катетке қатынасы.
-
Секанс — гипотенузаның жанама катетке қатынасы.
-
Косеканс — гипотенузаның қарама-қарсы жатқан катетке қатынасы.
Берілген анықтамалар функциялардың
сүйір бұрыштарға (0-ден π 2 {\displaystyle
\pi \over 2} ![]() радиан) қатысты мəндерін есептеуге
арналған.
радиан) қатысты мəндерін есептеуге
арналған.
Тригонометриялық функциялардың графиктері.
Бірлік шеңбердегі Ө бұрышына қатысты тригонометриялық функцияларды қарастырсақ (суретті қара):
-
θ {\displaystyle \theta }
 бұрышының Синусы "A"
нүктесінің ординатасы ретінде анықталады.
бұрышының Синусы "A"
нүктесінің ординатасы ретінде анықталады. -
Косинус — "A" нүктесінің абсциссасы.
-
Котангенс — косинустың синусқа қатынасы.

шағым қалдыра аласыз