
Жалпы білім беретін мектепте математиканы тереңдете оқу жүйесінде зерттеу есептері.
Абай облысы денсаулық сақтау басқармасының «Дүйсенбі Қалматаев атындағы мемлекеттік жоғарғы медицина колледжі»
Хамзина Асем Ахметоллақызы математика және физика пәндерінң оқытушысы
Еліміздің өркениетті елдер қатарына қосылып, егемендік алған тұста осы елдің келешегін жалғастырар, экономикасын, мәдениетін көтерер ұрпақ тәрбиелеу - бүгінгі күннің талабы. Бүгінгі қоғамның дамуы оның мүшелерінің білімімен өлшенетін кезі келді. Өйткені, қазіргі өркениетке жеткізетін құрал- тек қана білім. Білімді ұрпақ қана қоғамның болашақ иесі бола алады.
«Қазақстан Республикасының 2030 жылға дейінгі Даму стратегиясында» былай делінген:
«ХХІ ғасырда білімін дамыта алмаған елдің тығырыққа тірелері анық. Біз болашақтың жоғары технологиялық және ғылыми қамтымды өндірістері үшін кадрлар қорын жасақтауға тиіспіз. Осы заманғы білім беру жүйесінсіз әрі алысты барлап, кең ауқымда, жаңаша ойлай білетін осы заманғы басқарушыларсыз біз иновациялық экономика құра алмаймыз. Барлық деңгейдегі технологиялық және кәсіптік білім беруді дамытуға бағытталған тиісті шаралар қолдануымыз шарт»- деп «Қазақстан экономикалық, әлеуметтік және саяси жедел жаңару жолында» атты президент жолдауында атап көрсетілгендей бүгінгі күн мектептегі білім бері бағытында жаңаша көзқарасты талап етіп отыр.
Адамзат баласы өзі әр түрлі қиыр жолдармен келіп жеткен ХХІ ғасырды атом энергетикасы ғасыры, жаһандану ғасыры, математикаландыру ғасыры (және тағы басқа) деген сияқты әр түрлі атауда. Белгілі бір көзқараспен қарағанда мұның ешқайсысын да «олай емес», - деуге болмайды. Бірақ қазіргі ғасыр – ақпараттар тасқыны ғасыры екендігіне де күмән жоқ: сарапшылар барлық кездерде жазылған кітаптарға қарағанда, ақпараттардың 2006 жылы жаһандық ауқымда 3 миллион есе көп шығарылғанын есептеген. Болжам бойынша 2030 жылы ақпараттың бұл көлемі тағы да алты есе ұлғаймақ.
Бұл жағдайға байланысты қазір әлемнің көптеген дамыған елдеріндегідей біздің елімізде ауқымды шаралар қолға алынуда. Соның бірі ғана емес бірегейі, ол – бұл күнде ХХ ғасырдың еншісінде қалып бара жатқан белгілі бір уақыт кезеңінде ғана білім алу жағдайынан - бүкіл өмір бойы білім алу жағдайына көшу, яғни адамның бүкіл өмір бойы тұрақты түрде жаңа білім мен дағдыларды игерулеріне жағдай туғызу.
Сондықтан да қазіргі таңда білім беру жүйелерінің алдында тұрған негізгі міндет адамның бүкіл өмір бойы тұрақты түрде жаңа білімдерді ала алуларына және соған сәйкес оларды қолдана алу іскерліктерін игерулеріне, яғни шығармашылық тұлға ретінде қалыптасуына негіз қалау болып табылады. Бұл міндетті жүзеге асыру орта білім беру жүйесінде оқушыларды өз бетімен білім алуға ынталы ету, оларға жаңа білімді тек репродуктивтік қана емес ізденіс жүргізу және зерттеушілік қызметтерін дамыту арқылы игерту мәселелерінің практикада нақты шешімін табумен тығыз байланысты. Зерттеушілік қызмет оқушыларды жаңа білімді игеруге ғана бағыттап қоймай, жаңа ақыл-ой қызметінің қалыптасуына көмектеседі. Ал, бұл оқушылардың арнайы шығармашылық қабілетінің ғана емес, жалпы алғанда теориялық ой-пікірлерінің дамуына да зор ықпал етеді.
Мектептерде математика пәнін оқытудың алдында жалпы мақсаттармен қатар осы ғылымның ерекшеліктеріне сүйенетін спецификалық мақсаттар да тұр. Олардың бірі – математикалық ойлауды қалыптастыру және дамыту. Бұл оқушылардың математикалық жетістіктерінің пайда болуына және нәтижелі дамуына себеп болады.
Баланың интелектуалдық ойлау қабілетін үш бағытта жылдамдатуға болады: ойлаудың түсінікті құрылуы, сөйлеу интелектісі және жоспар құру.
Жақсы білімді қалыптастыру белгілі бір мақсатқа бағытталған ойлаусыз жүзеге аспайды, сондықтан ол қазіргі уақытта мектептегі оқытудың негізгі мақсаттарының бірі болып табылады.
Баланы ізденушілікке баулу, оған ғылыми зерттеу дағдысы мен білігін игерту бүгінгі білім беру саласының маңызды мәселесі болып саналады. Ғылыми зерттеу дегеніміз ғылыми әдіс-тәсілдерді қолдана отырып, белгілі бір объект жөнінде жаңа білім қалыптастырумен аяқталатын жүйелі және арнайы мақсатқа көзделген объектілермен танысу. Балаларды оқытуда зерттеу әдісін қолдану қажеттілігі олардың табиғи қызығушылығы қоршаған ортасына деген құштарлығының басымдылығымен түсіндіріледі. Оқушының өзіндік зерттеу әрекеті оның өзіндік талабын қанағаттандыруға ықпал етеді.
Зерттеуге қызығушылықты тудырудың маңызды алғышарты ретінде іс-әрекеттің кең әлеуметтік түрткілерін тәрбиелеу, оның мағынасын ұғыну, өз іс-әрекеті үшін зерттеп отырған үрдістерінің маңыздылығын түсіну болады. Осыған орай Аристотельдің мынандай сөзі бар: «Таң қалу арқылы адамдар философияға жақындай бастайды, олар алдындағы қиын мәселені шеше келе одан ары жолдың жалғасында одан да қиын мәселелердегі қиындықтарды түсінеді», яғни қызығушылық зерттеу әрекетінің қозғаушы күші. Қазіргі жас жектіншектердің негізгі міндеті – білім алу, ғылымды игеру. Білім-ғылымсыз ешбір қоғам алға баспайды, ешбір мемелекет күшеймейді.
Зерттеу есептерінің кейбір түрлерін атайық:
-зерттелетін математикалық объектілердің қасиеттерін анықтау немесе олардың арасындағы қатынастар;
-математиканың біраз фактісі бойынша жеке жағдайларды бөлу;
- бірқатар мәселелерді жалпылау;
-бірдей есепті әртүрлі тәсілдермен шешу;
-есептің шешімінен жаңа міндеттер құрстыру;
Американдық педагог-математик Дж. Пойаның айтуынша математиканы білу деген – есептерді шығара білу, яғни стандарттық есептерді ғана емес, ойлаудың еркіндігін, сананың салауаттылығын, өзіндік болмысты, тапқырлықты керек ететін есептерді шығару. Ол өзінің «Математические открытия», - деген еңбегінде оқыту үрдісінде оқушыларды өзіндік зерттеуге үйрететін есептерге тән үш сәтті салыстырмалы түрде атап көрсетті:
Сабақта үнемі оқушылардың өз бетімен жұмыс жасау қабілеттері мен танымдық қызығушылықтарының қалыптасуына көмектесетін тапсырмаларды пайдалану керек.
Оқушылармен жұмысты неғұрлым егжей-тегжейлі талдауға жүгінейік зерттеу есептерінің аталған түрлерін шешу.
Арнайы таңдап алынған жаттығулардың көмегімен оқушыларды берілген тапсырмаларды орындауға үйрету, оларды бақылауға үйрету, аналогияны, индукцияны, салыстыруды қолдану және қорытынды шығару.
1-есеп:Кейбір қалада үш жұп қиылысатын көшелер бар. Әрбір қиылыста бағдаршам орнатылған.
а) қалада қанша бағдаршам бар?
б) барлық ескілерді кесіп өтетін және бұрыннан бар қиылыстардан өтпейтін жаңа көше салу туралы шешім қабылданды. Қанша бағдаршам орнату керек?
в) егер көшелерді төсеу осылай жалғасатын болса, алты көшесі бар қалада қанша бағдаршам болады деп айтуға бола ма?
г) n көшелерімен?
а) алғашқы үш жұп көшелермен қиылысады-бұл үшбұрыш, барлығы үш бағдаршам.
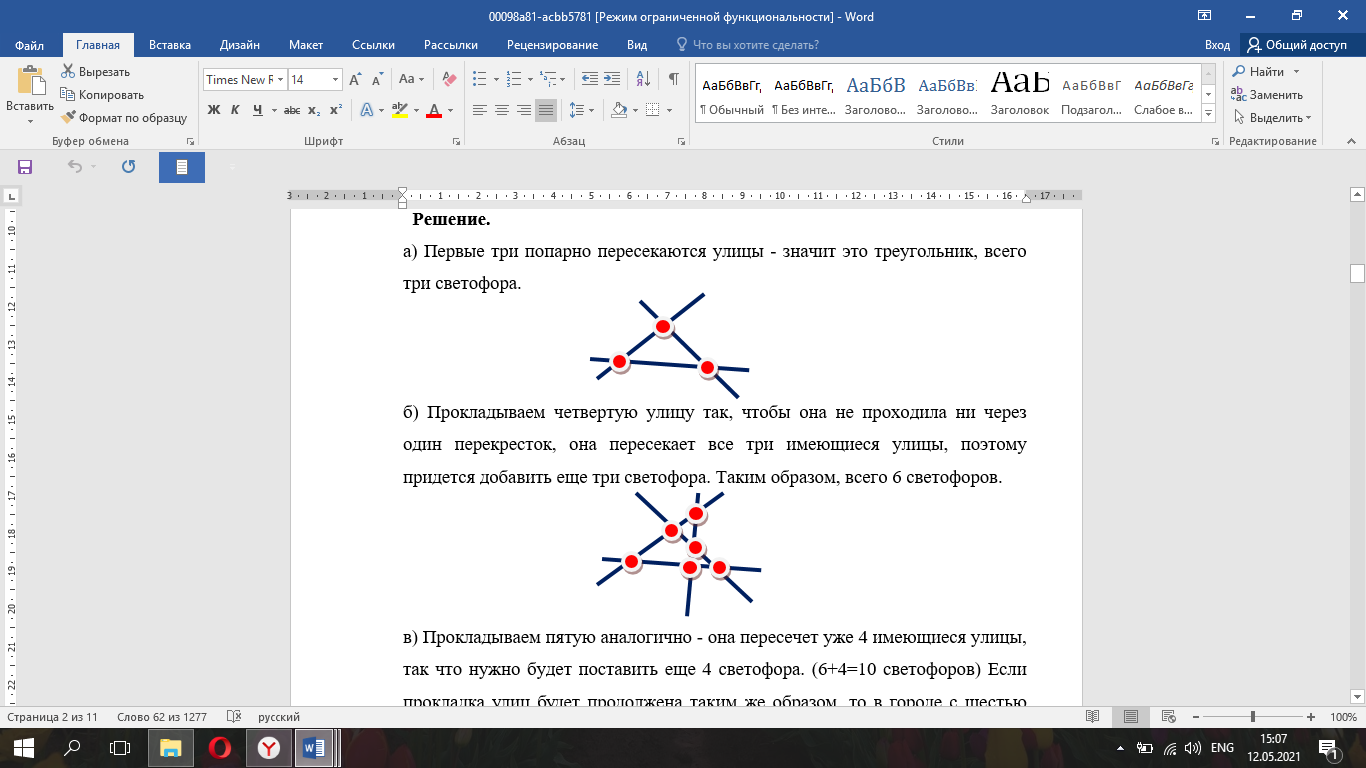
б) біз төртінші көшені кез-келген қиылыстан өтпейтін етіп саламыз, ол барлық үш көшені кесіп өтеді, сондықтан тағы үш бағдаршам қосуға тура келеді. Осылайша, барлығы 6 бағдаршам бар.

в) біз бесінші жолды осылай саламыз - ол қазірдің өзінде бар 4 көшені кесіп өтеді, сондықтан сізге тағы 4 бағдаршам қою керек болады. (6+4=10 бағдаршам) егер көшелерді төсеу осылай жалғасатын болса, онда қалада алты көше бағдаршамы болады (10+5=15 бағдаршам)
г) 3 көше - 3·(3-1)/2 =3 бағдаршам
4 көше – 4·4−12=6 бағдаршам
5 көше– 5·5−12=10 бағдаршам
6 көше– 6·6−12=15 светофоров
…..
n көше- n ∙ n−12 бағдаршам
Жауабы: а) 3; б) 6; в)15; г)n ∙ n−12
2-есеп.
1) Теңдікті тексеріңіз:1+3= ,
1+3+5=
,
1+3+5= ,
1+3+5+7=
,
1+3+5+7=
Бұл теңдіктер қатардағы тақ сандардың қосындысын есептеу әдісін ұсынады. Неде бұл тәсіл? Келесі теңдікті жазып, есептеулер арқылы өзіңізді тексеріңіз.
2) Қарастырылған техниканы пайдаланып, табыңыз:
а) алғашқы он тақ санның қосындысы:
б) 1-ден 99-ға дейінгі барлық тақ сандардың қосындысы.
Шешуі.
1)
1+3=
4+4
1+3+5=
9=9
1+3+5+7=
16=16
1+3+5+7+9=
25=25
Қорытынды: қосылғыштар саны кез
келген болғанда, алғашқы тақ сандар қосындысы қосылғыштар
санының квадратына тең. 2)1+3+5+7+9+11+13+15+17+19= =100
=100
3)1+3+5+7+…+99= =2025
=2025
3-есеп
12 қабатты үйдің лифтісіне 3 жолаушы отырған. Әрқайсысы бірдей ықтималдығы бар басқаларға қарамастан кез-келген қабатта (2-ші қабаттан бастап) шыға алады. Қанша жолмен:
1) Жолаушылар бір қабатта шыға алады (шығу тәртібі маңызды емес);
2) екі адам бір қабатқа, ал үшінші адам екінші қабатқа шыға алады;
3) адамдар әртүрлі қабаттарға шыға алады;
4) жолаушылар лифттен шыға ала ма?
Шешуі.
1)![]() шығу үшін 3 қабатты таңдауға болады.
шығу үшін 3 қабатты таңдауға болады.
2) ![]() Адамдарды әр үш қабатқа
орналасытру тәсілі.
Адамдарды әр үш қабатқа
орналасытру тәсілі.
3)Осыған сәйкес,
адамдар әртүрлі қабаттан шыға
алады.Мына![]() тәсілдер
арқылы.
тәсілдер
арқылы.
4) ![]() мына тәсілмен 1 адам лифтыдан
шыға алады,және
мына тәсілмен 1 адам лифтыдан
шыға алады,және
![]() мына тәсілмен 2 адам шыға
алады,және
мына тәсілмен 2 адам шыға
алады,және ![]() мына тәсілмен 3 адам шыға
алады.
мына тәсілмен 3 адам шыға
алады.
Комбинацияларды көбейту
ережесі бойынша: ![]() осы тәсілмен 3 адам шыға
алады.
осы тәсілмен 3 адам шыға
алады.
Жауабы: 1) 11; 2) 330; 3) 990; 4) 1331
4-есеп.Тырналар әдетте дұрыс үшбұрышты құрайтын етіп ұшады: алда бір тырна (көшбасшы), оның артында 2, содан кейін 3 тырна және т. б. Егер соңғы қатарда 15 дана санауға болатын болса, тырналар тобында қанша ұшты? n дана?
Шешуі.

Мәселені тұжырымдау кезеңінде барлық сандарды қатарынан қосу ұзақ және ыңғайсыз болатынына назар аударамыз. Қосудың оңай әдісін табу керек. Іздеу барысында сіз қосылғыштардың аз мәнін қолдана аласыз. Алдымен келесі тапсырманы қарастырыңыз: "жазбаларды қарастырып, соманы есептеу кезінде қалай ойлауға болатындығын түсіндіріңіз1 + 2 + 3 +... + 7 + 8".
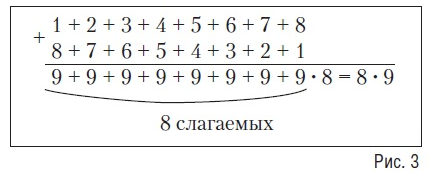
8 қосылғыштар
Бұл 1-ден 8-ге дейінгі сандардың екі еселенген қосындысы, сондықтан оны 2-ге бөлу керек. Теңдік пайда болды.
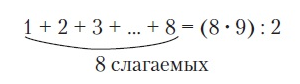
8 қосылғыштар
Бұл теңдікте алғашқы 8 санның қосындысы келесі санға терминдер санының көбейтіндісінің жартысына тең (немесе соңғы қосылғыштан) (яғни, соңғы қосылғыштан 1-ге көп).
Гипотезаны тексеру кезеңінде ұқсас қосындыны бейнелеуге болады 1 + 2 + 3 + 4 + 5 + 6 (басқа қосылғыштардың саны) сандық баспалдақ түрінде.
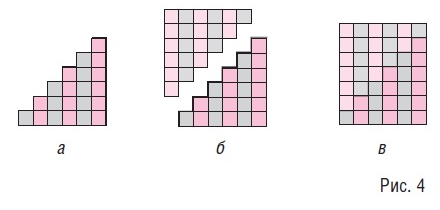
1 + 2 + 3 + 4 + 5 + 6;
(1 + 2 + 3 + 4 + 5 + 6) - 2;
6 - (6+1);
(1 + 2 + 3 + 4 + 5 + 6) - 2 = 6 - (6 + 1);
1 + 2 + 3 + 4 + 5 + 6 = 6 - (6 + 1): 2.
Осыдан кейін бастапқы мәселені шешу үшін қажетті есептеулер жасалады:
1 + 2 + 3 +... + 15 = (15∙ 16): 2 = 120 (тырналар).
Енді n тырналар үшін табамыз: 1 + 2 + 3 +... + n. n + 1 - бұл келесі n саны үшін. 1-ден n-ге дейінгі сандардың қосындысын табу үшін теңдікті (формуланы) жазамыз:
![]()
Жауабы: 120 тырна, n∙(n+1):2 тырна.
Мұғалімнің ғана қолынан келетін нәрсе-ол балалардың өз пәніне деген қызығушылығын өшіріп алмай, ары қарай жалғастыруы. Яғни, ойлау қабілетінің ерекшеліктерін дамыту, таным белсенділіктерін арттыру, қызығушылығын дамыту, барлық оқушыларға берілетін тапсырмалардан ерекше, күрделі тапсырмаларды беру, көбірек ойландыру, танымдық, логикалық ойындар беру арқылы қызығушылықтарын үстемдеу, проблемалық сұрақтармен мәселелерді шешуді, өз бетімен жұмыс істеуді үйрету, зерттеуге баулу қажет.
Осыған байланысты баланы зерттеу әрекетіне дайындау, оның зерттеушілік ізденіс білігі мен дағдыларын қалыптастыру қазіргі білім беру ісінің маңызды міндеті болып есептеледі. Бүгінгі баланың әлемде болашағына дұрыс таңдау жасай алатын, ұтымды шешім қабылдай алатын, сондай-ақ өзінің өміріндегі өзгерістер ағымына икемделе білетін қабілетіне байланысты өмір сүру тәртібі күтіп тұр. Баланың айналаны өз бетімен танып-білуге деген табиғи ұмтылысы негізінде құрылған оқытудағы зерттеу тәсілін пайдалану кіші жастағы оқушымен жұмыста ерекше орын алады.
Қазіргі жас жектіншектердің негізгі міндеті – білім алу, ғылымды игеру. Білім-ғылымсыз ешбір қоғам алға баспайды, ешбір мемелекет күшеймейді.
Келешек мемелекетіміздің тағдыры білімді жастарға байланысты, бұл туралы Елбасы былай дейді: «тұрақты дамуға қол жеткізу үшін біз интеллектуалдық элитаға, жоғарғы технологияға, еліміздің ғылыми әлеуетіне сүйенуіміз қажет. Тек өзінің интеллектуалдық әлеуетінің арқасында ғана ел әлемдегі өзінің орнын ала алады». Ал іздену жұмыстары оқушылардың зерттеу мәдениетін қалыптастырады.
Қолданылған әдебиеттер
-
Журнал «Математика Қазақстан мектебінде» №6, 2013 ж.
-
Журнал «Творческая педагогика»№3, 2010 ж.
-
Ж.А.Қараев «Деңгейлеп оқыту технологиясы»
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Жалпы білім беретін мектепте математиканы тереңдете оқу жүйесінде зерттеу есептері.
Жалпы білім беретін мектепте математиканы тереңдете оқу жүйесінде зерттеу есептері.
Жалпы білім беретін мектепте математиканы тереңдете оқу жүйесінде зерттеу есептері.
Абай облысы денсаулық сақтау басқармасының «Дүйсенбі Қалматаев атындағы мемлекеттік жоғарғы медицина колледжі»
Хамзина Асем Ахметоллақызы математика және физика пәндерінң оқытушысы
Еліміздің өркениетті елдер қатарына қосылып, егемендік алған тұста осы елдің келешегін жалғастырар, экономикасын, мәдениетін көтерер ұрпақ тәрбиелеу - бүгінгі күннің талабы. Бүгінгі қоғамның дамуы оның мүшелерінің білімімен өлшенетін кезі келді. Өйткені, қазіргі өркениетке жеткізетін құрал- тек қана білім. Білімді ұрпақ қана қоғамның болашақ иесі бола алады.
«Қазақстан Республикасының 2030 жылға дейінгі Даму стратегиясында» былай делінген:
«ХХІ ғасырда білімін дамыта алмаған елдің тығырыққа тірелері анық. Біз болашақтың жоғары технологиялық және ғылыми қамтымды өндірістері үшін кадрлар қорын жасақтауға тиіспіз. Осы заманғы білім беру жүйесінсіз әрі алысты барлап, кең ауқымда, жаңаша ойлай білетін осы заманғы басқарушыларсыз біз иновациялық экономика құра алмаймыз. Барлық деңгейдегі технологиялық және кәсіптік білім беруді дамытуға бағытталған тиісті шаралар қолдануымыз шарт»- деп «Қазақстан экономикалық, әлеуметтік және саяси жедел жаңару жолында» атты президент жолдауында атап көрсетілгендей бүгінгі күн мектептегі білім бері бағытында жаңаша көзқарасты талап етіп отыр.
Адамзат баласы өзі әр түрлі қиыр жолдармен келіп жеткен ХХІ ғасырды атом энергетикасы ғасыры, жаһандану ғасыры, математикаландыру ғасыры (және тағы басқа) деген сияқты әр түрлі атауда. Белгілі бір көзқараспен қарағанда мұның ешқайсысын да «олай емес», - деуге болмайды. Бірақ қазіргі ғасыр – ақпараттар тасқыны ғасыры екендігіне де күмән жоқ: сарапшылар барлық кездерде жазылған кітаптарға қарағанда, ақпараттардың 2006 жылы жаһандық ауқымда 3 миллион есе көп шығарылғанын есептеген. Болжам бойынша 2030 жылы ақпараттың бұл көлемі тағы да алты есе ұлғаймақ.
Бұл жағдайға байланысты қазір әлемнің көптеген дамыған елдеріндегідей біздің елімізде ауқымды шаралар қолға алынуда. Соның бірі ғана емес бірегейі, ол – бұл күнде ХХ ғасырдың еншісінде қалып бара жатқан белгілі бір уақыт кезеңінде ғана білім алу жағдайынан - бүкіл өмір бойы білім алу жағдайына көшу, яғни адамның бүкіл өмір бойы тұрақты түрде жаңа білім мен дағдыларды игерулеріне жағдай туғызу.
Сондықтан да қазіргі таңда білім беру жүйелерінің алдында тұрған негізгі міндет адамның бүкіл өмір бойы тұрақты түрде жаңа білімдерді ала алуларына және соған сәйкес оларды қолдана алу іскерліктерін игерулеріне, яғни шығармашылық тұлға ретінде қалыптасуына негіз қалау болып табылады. Бұл міндетті жүзеге асыру орта білім беру жүйесінде оқушыларды өз бетімен білім алуға ынталы ету, оларға жаңа білімді тек репродуктивтік қана емес ізденіс жүргізу және зерттеушілік қызметтерін дамыту арқылы игерту мәселелерінің практикада нақты шешімін табумен тығыз байланысты. Зерттеушілік қызмет оқушыларды жаңа білімді игеруге ғана бағыттап қоймай, жаңа ақыл-ой қызметінің қалыптасуына көмектеседі. Ал, бұл оқушылардың арнайы шығармашылық қабілетінің ғана емес, жалпы алғанда теориялық ой-пікірлерінің дамуына да зор ықпал етеді.
Мектептерде математика пәнін оқытудың алдында жалпы мақсаттармен қатар осы ғылымның ерекшеліктеріне сүйенетін спецификалық мақсаттар да тұр. Олардың бірі – математикалық ойлауды қалыптастыру және дамыту. Бұл оқушылардың математикалық жетістіктерінің пайда болуына және нәтижелі дамуына себеп болады.
Баланың интелектуалдық ойлау қабілетін үш бағытта жылдамдатуға болады: ойлаудың түсінікті құрылуы, сөйлеу интелектісі және жоспар құру.
Жақсы білімді қалыптастыру белгілі бір мақсатқа бағытталған ойлаусыз жүзеге аспайды, сондықтан ол қазіргі уақытта мектептегі оқытудың негізгі мақсаттарының бірі болып табылады.
Баланы ізденушілікке баулу, оған ғылыми зерттеу дағдысы мен білігін игерту бүгінгі білім беру саласының маңызды мәселесі болып саналады. Ғылыми зерттеу дегеніміз ғылыми әдіс-тәсілдерді қолдана отырып, белгілі бір объект жөнінде жаңа білім қалыптастырумен аяқталатын жүйелі және арнайы мақсатқа көзделген объектілермен танысу. Балаларды оқытуда зерттеу әдісін қолдану қажеттілігі олардың табиғи қызығушылығы қоршаған ортасына деген құштарлығының басымдылығымен түсіндіріледі. Оқушының өзіндік зерттеу әрекеті оның өзіндік талабын қанағаттандыруға ықпал етеді.
Зерттеуге қызығушылықты тудырудың маңызды алғышарты ретінде іс-әрекеттің кең әлеуметтік түрткілерін тәрбиелеу, оның мағынасын ұғыну, өз іс-әрекеті үшін зерттеп отырған үрдістерінің маңыздылығын түсіну болады. Осыған орай Аристотельдің мынандай сөзі бар: «Таң қалу арқылы адамдар философияға жақындай бастайды, олар алдындағы қиын мәселені шеше келе одан ары жолдың жалғасында одан да қиын мәселелердегі қиындықтарды түсінеді», яғни қызығушылық зерттеу әрекетінің қозғаушы күші. Қазіргі жас жектіншектердің негізгі міндеті – білім алу, ғылымды игеру. Білім-ғылымсыз ешбір қоғам алға баспайды, ешбір мемелекет күшеймейді.
Зерттеу есептерінің кейбір түрлерін атайық:
-зерттелетін математикалық объектілердің қасиеттерін анықтау немесе олардың арасындағы қатынастар;
-математиканың біраз фактісі бойынша жеке жағдайларды бөлу;
- бірқатар мәселелерді жалпылау;
-бірдей есепті әртүрлі тәсілдермен шешу;
-есептің шешімінен жаңа міндеттер құрстыру;
Американдық педагог-математик Дж. Пойаның айтуынша математиканы білу деген – есептерді шығара білу, яғни стандарттық есептерді ғана емес, ойлаудың еркіндігін, сананың салауаттылығын, өзіндік болмысты, тапқырлықты керек ететін есептерді шығару. Ол өзінің «Математические открытия», - деген еңбегінде оқыту үрдісінде оқушыларды өзіндік зерттеуге үйрететін есептерге тән үш сәтті салыстырмалы түрде атап көрсетті:
Сабақта үнемі оқушылардың өз бетімен жұмыс жасау қабілеттері мен танымдық қызығушылықтарының қалыптасуына көмектесетін тапсырмаларды пайдалану керек.
Оқушылармен жұмысты неғұрлым егжей-тегжейлі талдауға жүгінейік зерттеу есептерінің аталған түрлерін шешу.
Арнайы таңдап алынған жаттығулардың көмегімен оқушыларды берілген тапсырмаларды орындауға үйрету, оларды бақылауға үйрету, аналогияны, индукцияны, салыстыруды қолдану және қорытынды шығару.
1-есеп:Кейбір қалада үш жұп қиылысатын көшелер бар. Әрбір қиылыста бағдаршам орнатылған.
а) қалада қанша бағдаршам бар?
б) барлық ескілерді кесіп өтетін және бұрыннан бар қиылыстардан өтпейтін жаңа көше салу туралы шешім қабылданды. Қанша бағдаршам орнату керек?
в) егер көшелерді төсеу осылай жалғасатын болса, алты көшесі бар қалада қанша бағдаршам болады деп айтуға бола ма?
г) n көшелерімен?
а) алғашқы үш жұп көшелермен қиылысады-бұл үшбұрыш, барлығы үш бағдаршам.

б) біз төртінші көшені кез-келген қиылыстан өтпейтін етіп саламыз, ол барлық үш көшені кесіп өтеді, сондықтан тағы үш бағдаршам қосуға тура келеді. Осылайша, барлығы 6 бағдаршам бар.

в) біз бесінші жолды осылай саламыз - ол қазірдің өзінде бар 4 көшені кесіп өтеді, сондықтан сізге тағы 4 бағдаршам қою керек болады. (6+4=10 бағдаршам) егер көшелерді төсеу осылай жалғасатын болса, онда қалада алты көше бағдаршамы болады (10+5=15 бағдаршам)
г) 3 көше - 3·(3-1)/2 =3 бағдаршам
4 көше – 4·4−12=6 бағдаршам
5 көше– 5·5−12=10 бағдаршам
6 көше– 6·6−12=15 светофоров
…..
n көше- n ∙ n−12 бағдаршам
Жауабы: а) 3; б) 6; в)15; г)n ∙ n−12
2-есеп.
1) Теңдікті тексеріңіз:1+3= ,
1+3+5=
,
1+3+5= ,
1+3+5+7=
,
1+3+5+7=
Бұл теңдіктер қатардағы тақ сандардың қосындысын есептеу әдісін ұсынады. Неде бұл тәсіл? Келесі теңдікті жазып, есептеулер арқылы өзіңізді тексеріңіз.
2) Қарастырылған техниканы пайдаланып, табыңыз:
а) алғашқы он тақ санның қосындысы:
б) 1-ден 99-ға дейінгі барлық тақ сандардың қосындысы.
Шешуі.
1)
1+3=
4+4
1+3+5=
9=9
1+3+5+7=
16=16
1+3+5+7+9=
25=25
Қорытынды: қосылғыштар саны кез
келген болғанда, алғашқы тақ сандар қосындысы қосылғыштар
санының квадратына тең. 2)1+3+5+7+9+11+13+15+17+19= =100
=100
3)1+3+5+7+…+99= =2025
=2025
3-есеп
12 қабатты үйдің лифтісіне 3 жолаушы отырған. Әрқайсысы бірдей ықтималдығы бар басқаларға қарамастан кез-келген қабатта (2-ші қабаттан бастап) шыға алады. Қанша жолмен:
1) Жолаушылар бір қабатта шыға алады (шығу тәртібі маңызды емес);
2) екі адам бір қабатқа, ал үшінші адам екінші қабатқа шыға алады;
3) адамдар әртүрлі қабаттарға шыға алады;
4) жолаушылар лифттен шыға ала ма?
Шешуі.
1)![]() шығу үшін 3 қабатты таңдауға болады.
шығу үшін 3 қабатты таңдауға болады.
2) ![]() Адамдарды әр үш қабатқа
орналасытру тәсілі.
Адамдарды әр үш қабатқа
орналасытру тәсілі.
3)Осыған сәйкес,
адамдар әртүрлі қабаттан шыға
алады.Мына![]() тәсілдер
арқылы.
тәсілдер
арқылы.
4) ![]() мына тәсілмен 1 адам лифтыдан
шыға алады,және
мына тәсілмен 1 адам лифтыдан
шыға алады,және
![]() мына тәсілмен 2 адам шыға
алады,және
мына тәсілмен 2 адам шыға
алады,және ![]() мына тәсілмен 3 адам шыға
алады.
мына тәсілмен 3 адам шыға
алады.
Комбинацияларды көбейту
ережесі бойынша: ![]() осы тәсілмен 3 адам шыға
алады.
осы тәсілмен 3 адам шыға
алады.
Жауабы: 1) 11; 2) 330; 3) 990; 4) 1331
4-есеп.Тырналар әдетте дұрыс үшбұрышты құрайтын етіп ұшады: алда бір тырна (көшбасшы), оның артында 2, содан кейін 3 тырна және т. б. Егер соңғы қатарда 15 дана санауға болатын болса, тырналар тобында қанша ұшты? n дана?
Шешуі.

Мәселені тұжырымдау кезеңінде барлық сандарды қатарынан қосу ұзақ және ыңғайсыз болатынына назар аударамыз. Қосудың оңай әдісін табу керек. Іздеу барысында сіз қосылғыштардың аз мәнін қолдана аласыз. Алдымен келесі тапсырманы қарастырыңыз: "жазбаларды қарастырып, соманы есептеу кезінде қалай ойлауға болатындығын түсіндіріңіз1 + 2 + 3 +... + 7 + 8".

8 қосылғыштар
Бұл 1-ден 8-ге дейінгі сандардың екі еселенген қосындысы, сондықтан оны 2-ге бөлу керек. Теңдік пайда болды.
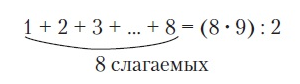
8 қосылғыштар
Бұл теңдікте алғашқы 8 санның қосындысы келесі санға терминдер санының көбейтіндісінің жартысына тең (немесе соңғы қосылғыштан) (яғни, соңғы қосылғыштан 1-ге көп).
Гипотезаны тексеру кезеңінде ұқсас қосындыны бейнелеуге болады 1 + 2 + 3 + 4 + 5 + 6 (басқа қосылғыштардың саны) сандық баспалдақ түрінде.

1 + 2 + 3 + 4 + 5 + 6;
(1 + 2 + 3 + 4 + 5 + 6) - 2;
6 - (6+1);
(1 + 2 + 3 + 4 + 5 + 6) - 2 = 6 - (6 + 1);
1 + 2 + 3 + 4 + 5 + 6 = 6 - (6 + 1): 2.
Осыдан кейін бастапқы мәселені шешу үшін қажетті есептеулер жасалады:
1 + 2 + 3 +... + 15 = (15∙ 16): 2 = 120 (тырналар).
Енді n тырналар үшін табамыз: 1 + 2 + 3 +... + n. n + 1 - бұл келесі n саны үшін. 1-ден n-ге дейінгі сандардың қосындысын табу үшін теңдікті (формуланы) жазамыз:
![]()
Жауабы: 120 тырна, n∙(n+1):2 тырна.
Мұғалімнің ғана қолынан келетін нәрсе-ол балалардың өз пәніне деген қызығушылығын өшіріп алмай, ары қарай жалғастыруы. Яғни, ойлау қабілетінің ерекшеліктерін дамыту, таным белсенділіктерін арттыру, қызығушылығын дамыту, барлық оқушыларға берілетін тапсырмалардан ерекше, күрделі тапсырмаларды беру, көбірек ойландыру, танымдық, логикалық ойындар беру арқылы қызығушылықтарын үстемдеу, проблемалық сұрақтармен мәселелерді шешуді, өз бетімен жұмыс істеуді үйрету, зерттеуге баулу қажет.
Осыған байланысты баланы зерттеу әрекетіне дайындау, оның зерттеушілік ізденіс білігі мен дағдыларын қалыптастыру қазіргі білім беру ісінің маңызды міндеті болып есептеледі. Бүгінгі баланың әлемде болашағына дұрыс таңдау жасай алатын, ұтымды шешім қабылдай алатын, сондай-ақ өзінің өміріндегі өзгерістер ағымына икемделе білетін қабілетіне байланысты өмір сүру тәртібі күтіп тұр. Баланың айналаны өз бетімен танып-білуге деген табиғи ұмтылысы негізінде құрылған оқытудағы зерттеу тәсілін пайдалану кіші жастағы оқушымен жұмыста ерекше орын алады.
Қазіргі жас жектіншектердің негізгі міндеті – білім алу, ғылымды игеру. Білім-ғылымсыз ешбір қоғам алға баспайды, ешбір мемелекет күшеймейді.
Келешек мемелекетіміздің тағдыры білімді жастарға байланысты, бұл туралы Елбасы былай дейді: «тұрақты дамуға қол жеткізу үшін біз интеллектуалдық элитаға, жоғарғы технологияға, еліміздің ғылыми әлеуетіне сүйенуіміз қажет. Тек өзінің интеллектуалдық әлеуетінің арқасында ғана ел әлемдегі өзінің орнын ала алады». Ал іздену жұмыстары оқушылардың зерттеу мәдениетін қалыптастырады.
Қолданылған әдебиеттер
-
Журнал «Математика Қазақстан мектебінде» №6, 2013 ж.
-
Журнал «Творческая педагогика»№3, 2010 ж.
-
Ж.А.Қараев «Деңгейлеп оқыту технологиясы»

шағым қалдыра аласыз















