Линейные уравнения с двумя переменными

На данном уроке мы рассмотрим уравнение с двумя переменными, дадим его определение и построим график.

Напоминание теоретического материала и формулировка определения линейного уравнения с двумя переменными

Мы познакомились с понятиями координатной оси и координатной плоскости.  Мы знаем, что каждая точка плоскости однозначно задает пару чисел (х; у), причем первое число есть абсцисса точки, а второе – ордината.

Мы будем очень часто встречаться с линейным уравнением с двумя переменными, решением которого и есть пара чисел, которую можно представить на координатной плоскости.

Уравнение вида:

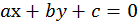, где a, b, с – числа, причем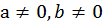 

Называется линейным уравнением с двумя переменными х и у. Решением такого уравнения будет любая такая пара чисел х и у, подставив которую в уравнение мы получим верное числовое равенство.

Пара чисел будет изображаться на координатной плоскости в виде точки.

У таких уравнений мы увидим много решений, то есть много пар чисел, и все соответствующие точки будут лежать на одной прямой.

Изучение алгоритма построения графика уравнения на примере

Рассмотрим пример:

Пример 1:

;  ;  ;

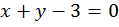
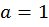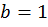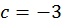Чтобы найти решения данного уравнения нужно подобрать соответствующие пары чисел х и у:

Пусть 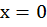 , тогда исходное уравнение превращается в уравнение с одной неизвестной:

, 

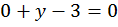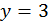
То есть, первая пара чисел, являющаяся решением заданного уравнения (0; 3). Получили точку А(0; 3)

Пусть 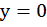 . Получим исходное уравнение с одной переменной: 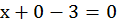 , отсюда  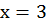, получили точку В(3; 0)

Занесем пары чисел в таблицу:

Построим на графике точки и проведем прямую:

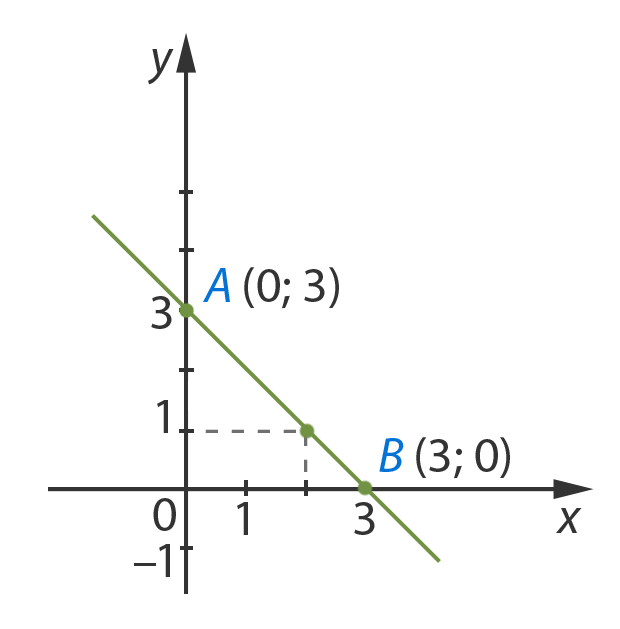
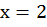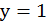Отметим, что любая точка на данной прямой будет решением заданного уравнения. Проверим – возьмем точку с координатой   и по графику найдем ее вторую координату. Очевидно, что в этой точке  . Подставим данную пару чисел в уравнение. Получим 0=0 – верное числовое равенство, значит точка, лежащая на прямой, является решением.

Пока доказать, что любая точка, лежащая на построенной прямой является решением уравнения, мы не можем, поэтому принимаем это за правду и докажем позже.

Решение примера

Пример 2 – построить график уравнения:

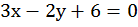
Составим таблицу, нам достаточно для построения прямой двух точек, но возьмем третью для контроля:

В первой колонке мы взяли удобный 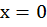 , найдем у:

,  , 

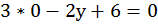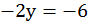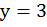
Во втором столбике мы взяли удобный 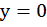 , найдем х:

,  ,  , 

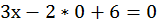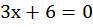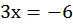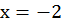
Возьмем для проверки 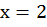  и найдем у:

,  , 

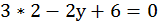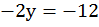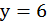
Построим график:

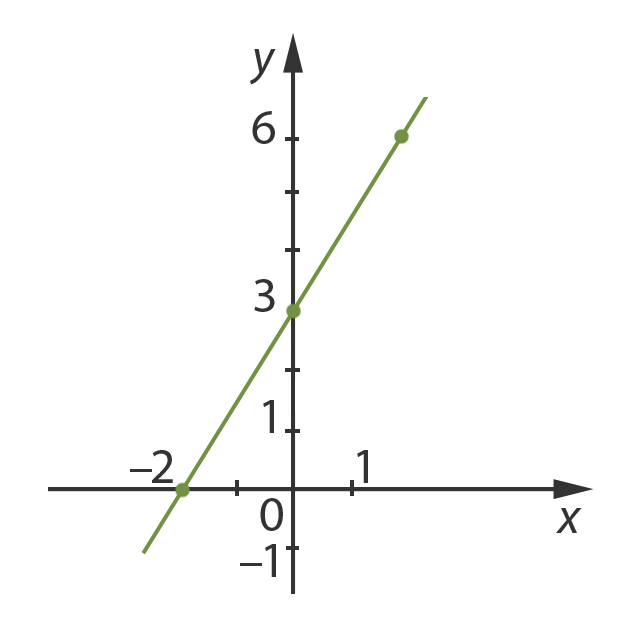
Умножим заданное уравнение на два:

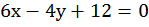
От такого преобразования множество решений не изменится и график останется таким же самым.

Выводы по уроку

Вывод: мы научились решать уравнения с двумя переменными и строить их графики, узнали, что графиком подобного уравнения есть прямая и что любая точка этой прямой является решением уравнения