Оқушымен бірге ғылыми жұмыс: Жапондық көбейтудің сызықтық алгоритмі

Ақтөбе қаласы «Ақбөбек» мектебі

Тақырыбы

Жапондық көбейтудің сызықтық алгоритмі

Секциясы

Математика-информатика

Зерттеуші

Ақтөбе қаласы «Ақбөбек» мектебінің

4-сынып оқушысы

Болатов Бекнар Бақытжанұлы

Жетекшісі

Ақтөбе қаласы «Ақбөбек» мектебінің

бастауыш класс мұғалімі

Сейлханова Рысгул Мирхановна

2021-2022 оқу жылы

А Н Н О Т А Ц И Я

Өмірдің әрқайсысы әртүрлі есептерді, соның ішінде екі таңбалы сандарды көбейтуге тура келеді. Мектепте біз сандарды «бағанда» көбейтуге үйретеміз. Интернетте қызықты және тез көбейту әдісін көрсеткен бейне көрдім. Бұл әдіс жапондық көбейтудің алгоритмі деп аталды. Ол әдіс арқылы көбейту кестесін білмейтін оқушылардың өзі екі немесе үш таңбалы сандарды көбете береді.

А Н Н О Т А Ц И Я

Каждый из жизни приходится увеличивать различные задачи, в том числе двузначные цифры. В школе мы учим размножению чисел в "столбце". В Интернете я увидел видео, которое показало интересный и быстрый способ размножения. Этот метод назывался японским размножением. Он позволяет учащимся, не знающим таблицу умножения, увеличить две или трехзначные числа.

A N N O T A T I O N

Each of life has to increase a variety of tasks, including double digits. At school, we teach the multiplication of numbers in the "column". On the Internet I saw a video that showed an interesting and fast way of reproduction. This method was called Japanese reproduction. It allows students who do not know the multiplication table to increase two or three-digit numbers.

1. Жобаның өзектілігі. Дамыған елдердің арасында Жапон, Қытай халықтарының ойлап табуымен ең оңай және ең тиімді тәсіл боп саналатын көбейту кестесі қазіргі таңда барлық елдерде пайдаланылып келеді. Оның тиімділігінің өзі көбейту кестесін жатқа білмеген оқушының өзі реттік қосу арқылы көбейту амалын шығара алады.

2.Гипотеза: Өзім сияқты балаларға, құрбыларыма көбейту тәсілінің ең оңай түрін үйренуді ұсыну.

3.Жобаны жазуға түрткі болған: Ғаламтор бетіндегі шимайланған сызықтарды әуелде түсінбей оның видеосын қарай бастадым. Содан кейін оның шығарылу жолын үйреніп алып, қызыққаным сонша бірнеше есептерді шығарып тастадым.

4. Жобаның мақсаты: Осы жұмысты орындағанда қойған мақсатым:

Сандарды көбейту кезінде көбейту кестесінің көмегінсіз шығаруға болатындығын насихаттау.

5. Міндеттері:

Өзге елдердегі көбейту тәсілінің түрлерін анықтау

Жапондық көбейту тәсілінің шығарылу жолын және тиімділігін анықтау

6. Зерттеу нысаны: Күнделікті математика сабағы

7. Зерттеу жұмысының әдіснамалы және теориялық негіздері:

Ғылыми зерттеулерге қойылатын теориялық талаптарға сай ғылыми деректер топтамаларына және осы бағыттағы арнайы мерзімдік басылымдарды, жарияланған материалдар мен ресми құжаттарға, келісім-шарттарға арқа сүйей отырып зерттеудің теориялық тұжырымдарын жасау. Әдістемелік негіздері ғылыми дәйектілік пен обьективті дәлдікті тұжырымдау

8. Жобаның дерек көздері: ғылыми жобада математика бағыты бойынша ғалымдардың зерттеу мәселесі бойынша жарық көрген әдебиеттері, мақалалары, пікірлері негізгі дерек көздері болды.

9. Зерттеудің базасы: Ақтөбе қаласының «Ақбөбек» мектебінің математика сабағында екі таңбалы сандарды көбейту.

10. Жұмыстың ғылыми жаңашылдығы ретінде ғаламтордағы, әдеби әдебиеттердегі сандарды көбейту жолдарын іздеу
Көбейтудің әртүрлі әдістерін меңгеру
Жапондық көбейту әдісін түсіну.
Екі таңбалы сандарды көбейтудің жапондық әдісімен көбейту құрылғысын жасау

11. Жұмыстың практикалық маңызы: Зерттеу барысында жасалған тұжырымдамалар, алынған мәліметтер математика сабағында тиімді әдістердің бірі боп саналады.

Ал көрсетілген іс-шаралар тізімі математика сабағынан кез келген оқушының қызығушылығын арттырады және оны практика жүзінде іске асыруға болады

МАЗМҰНЫ

1.Кіріспе.Көбейту және Пифагор кестесі

• 1.1.Көбейту кестесінің тарихы

2.Негізгі бөлім. Жапондық көбейтудің сызықтық алгоритмі

• 2.1.Жапондық көбейту тәсілі

• 2.2.Мультипликатор

• 2.3.Жапондық көбейту тәсілінің әдістері

• 2.4.Көбейту кестесін матрицаға орналастыру

• 2.5.Үш таңбалы санды екі таңбалы санға көбейту

3.Қорытынды.

Жапондық сызықтық алгоритмдер арқылы есептер шығару

• 3.1Жапондық көбейту тәсілін мектеп бағдарламасына енгізуді ұсыну

Пайдаланылған әдебиеттер

КІРІСПЕ

Көбейту кестесінің тарихы

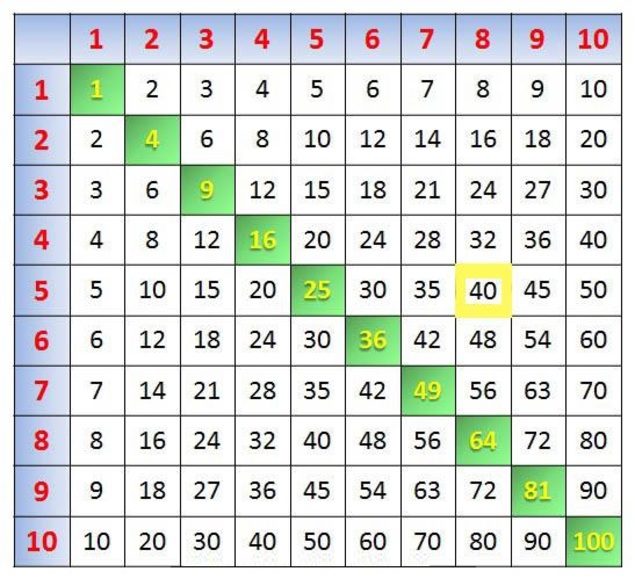
Көбейту кестесі – Пифагор кестесі ретінде халыққа бұрыннан таныс. Сондықтан оны ( 1-сурет) Пифагорлық кесте деп атайды. Алғашқы көбейту кестесінен жеңіл болсын деп, заманауи сипатқа өзгерткен. Алайда, зерттеушілер ескі кестені қолдану әлдеқайда оңай деп есептейді. (1 сурет) Көбейту — көбейткіштер (   a және   b ) деп аталатын екі объектіден көбейтінді деп аталатын үшінші объекті (   x ) тұрады . Жалпы алғанда көбейту — әр түрлі бинарлық (латынша — қос, екі деген сөз) амалдардың (сандарды, матрицаларды, векторларды, топтардың элементтерін, сақиналарды көбейту) атауы болып табылады.

(1-сурет)

Мектепте оқыған бағандардағы сандарды көбейту жолынан гөрі, көбейту оңай болуы мүмкін бе? Мәселен, бізде өмірдің әрқайсысы әртүрлі есептерді, соның ішінде екі таңбалы сандарды көбейтуге тура келеді. (2-сурет)

(2-сурет)

Көбейту - бірнеше бірдей сандарды қосудың ерекше жағдайы. Ертеде адамдар сандарды санау арқылы көбейтуді үйренді. Сонымен, 17, 18, 19, 20 сандары бойынша санау керек, олар 20-дан 10 + 10-ға дейін ғана емес, сонымен қатар екі ондық, яғни 2-10; 30 - он үш сөз, яғни он үш рет қайталау үшін үш рет - 3 · 10 - және тағы басқалар деп шешкен.

https://massaget.kz/layfstayl/bilim/naty-ylymdar/46345/

Негізгі бөлім

Жапондық көбейту тәсілі

И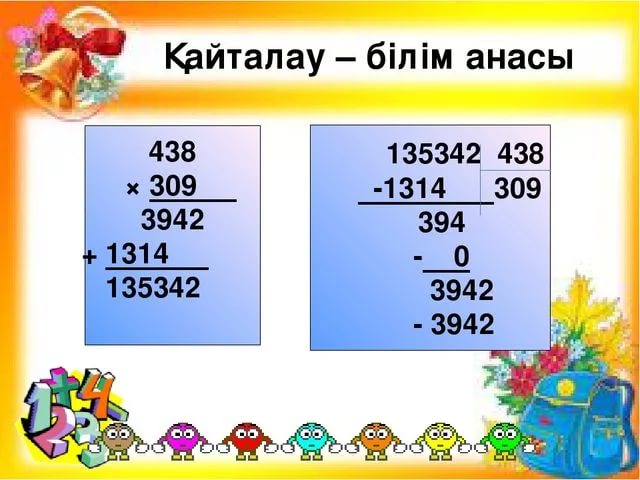
нтернетте қызықты және тез көбейту әдісін көрсеткен бейне көрдім. Осы әдісті зерттеуге кірісті, бұл әдіс жапондық көбейту деп аталды. Бұл сандарды көбейтудің жалғыз жолы және олар барлық елдерде әрдайым көбейе ме? Мек тепте біз сандарды «бағандап» көбейтуге үйретеміз. (3,4-сурет)

(3,4-сурет)

Жапонияда ежелгі дәуірдің өзінде бүтін сандардың өнімдерін есептеудің түпнұсқасы ыңғайлы еді. Басқа елдерде, соның ішінде Ресейде, бұл әдіс белгісіз болатын. Алайда, осы зерттеуде ұсынылған жетілдіруді есепке ала отырып, жапондық көбейтілім әдісі стандартты бағанды көбейту әдісін қолдана отырып сандардың өнімдерін есептеуде қиындықтарға ұшыраған оқушылар үшін математикалық есептеулерді орындау үшін сәтті қолданылады.

Қоғамның дамуының басында, егер адам көп мөлшерде қажет болмаса, онда бір қолдың саусақтарымен, содан кейін екі саусағымен, одан ары үш саусақтарымен және одан да көп саусақтармен есептеген. Кейінірек саусақтар жеткіліксіз болатын заттардың санын қайта санау қажет болған. Біртіндеп жаңа шоттар ойлап тапты. Африкаға кейбір тайпалар әлі күнге дейін тау-кен және жаңғақтарға сүйенеді. Тынық мұхиты аралдарының әрқайсысы 10-ға жеткен сайын кішкентай саңырауқұлақты және 100-ге жеткен кезде үлкен мөлшерде кокос жаңғақтарын есептейді. Сөйтіп көптеген жылдар өтті. Биржалық және сауда-саттық әзірленді, бұл сандардағы іс-әрекеттерде шот бойынша адамдардан жаңа дағдыларды талап етті.

Адамдар қосуға қарағанда көбейтуді кеш бастады. Вавилонда сандарды көбейту кезінде олар арнайы көбейтілім кестелерін - заманауи «ата-бабаларын» қолданды. Ежелгі Үндістанда сандарды көбейту әдісі ертеден қолданылады сонымен қатар қазіргі заманға сай. Үндістандар сандарды көбінежазбаша көбейтеді. Осылайша, Үндістан математиктері бірден құмға немесе ақылға аралық есептерді орындайтын өнімді жазды. Үнділік көбейту әдісі арабтарға берілді. Бірақ арабтар сандарды өшірмеді, бірақ оларды қиып, қиып алынған үстіне жаңа нөмірді жазды. Еуропада көптен бері өнім көбейтудің сомасы деп аталды. «Мультипликатор» атауы 6-шы ғасырдың шығармаларында және «мультипликативтік» - XIII ғасырда жазылды.

ХХVІІ- ғасырда математиктердің кейбірі көлбеу кросс-х-мен көбейтуді бастады, ал басқалары бұл үшін (·) нүктені қолданды.

XVIII ғасырдың аяғында ғана математиктердің көбісі нүктені көбейту символы ретінде қолдануға кірісті, бірақ олар сондай-ақ көлбеу крестті пайдалануға мүмкіндік берді. Көптеген белгілер (•, x) және теңдік белгісі (=) әйгілі неміс математикы Готфрид Вильгельм Лейбництің (1646-1716) билігінің арқасында танылды. Археологтар үстелдің көмегімен ескі Жапония мен Қытайда өткізілгенін растайтын жазбалардың үзінділері бар ағаш табақтарды бірнеше рет тапты. Жапонияның Нара қаласындағы қазба жұмыстары туралы VIII ғасырға байланысты таблетка табылды. Бұған дейін Киотоға жақын орналасқан басқа бір жапон астанасы Хейнан орналасқан, кейінірек 10-11 ғасырларға жататын үстелдер ашылды. Ең қызығы, Nara-да табылған планшет VII-X ғасырдың ежелгі қытай әріптеріне ұқсас, иероглифтерде жазылған.

Жапон көбейту әдісінің тәсілдері
Әртүрлі елдерде оқыту әдістері әртүрлі екенін құпия емес. Бірнеше он жыл бұрын Кеңес әлемдегі ең мықты мектептік жүйе деп саналды. Бірақ тіпті КСРО-да олар балаларға математикаға оқытудың қызықты әдістерін қолданған жоқ.
Мысалы, Жапонияда бірінші сынып оқушылары көбейту кестесін білмей, үш таңбалы сандарды көбейте алады. Ол үшін сызбалық жолақтармен қарапайым әдісті қолданыңыз. Әдістің логикасы суреттен анық көрінеді

Жапон археологтары 8-ші ғасырда жасалған көбейту үстелінің фрагменті ағаш таблетка тапты. Ғалымдардың пікірінше, мұндай кестелер жапондық империялық шенеуніктермен пайдаланылды, олар арифметиканы қоса алғанда әртүрлі ғылымдарды игеру керек еді.

Алынған таблетка бұрын Жапонияда табылған ең көне әдіс болып табылады. Бір қызығы, сандар жазылған иероглифтер 7-10-шы ғасырлардағы Танг қытай әулеті кезінде ресми хат ретінде пайдаланылған стильде өте ұқсас. Осыған сүйене отырып, ғалымдар үстелдің сол уақыттағы арифметиканың қытайлық оқулықтан көшірілгенін, яғни жапон көбейту кестесінің Қытайдан алынғанын ұсынды. Көршілеріне арифметика сияқты әртүрлі ғылымдарды үйрену үшін жоғары дәрежелі жапондар жыл сайын Қытайға аттанды.

Ежелгі қытайлық көбейту кестесі оңай емес, себебі ол екі таңбалы сандарды бір-бірімен көбейтуді қамтиды. Барлық жапон шенеуніктер мұндай үстелді жаттап алу мүмкін емес, сондықтан олармен бірге шұлықтар тәрізді бір нәрсе жасауға тырысады, олардың бірі фрагменті Жапониядағы археологтардың белгісі. Осылайша, кейбір арифметикалық жүйені құрушылар арасында жапон көбейткіштері кестесінен алынған, ол көбінесе 2700-3000 жылдардағы ғалымдардың бағалауы бойынша, көбейту үстелінің фрагменттері бар археологиялық табылғандармен дәлелденген.

Мысал: жапон әдісімен 13 · 24 есептейміз. Төмендегі суретті сызамыз (5-сурет):
Бірінші фактор 13 дегеніміз - бір көлденең сызық (бір он) және тағы үш көлденең сызық (үш бірлік).
Екінші фактор 24 дегеніміз - екі тік сызық (екі ондық) және тағы 4 жол (төрт бірлік).
Нәтиже: бірліктер саны - шаршы алаңда нүктелер саны (сызықтардың қиылысы) (12, яғни, біз 2 және 1-ге жазамыз); ондаған саны - сопақшадағы нүктелер саны (10 + 1 = 1, содан кейін біз 1 және 1 жүзге қарай жазамыз); жүздер саны - шеңберге нүктелер саны (2 + 1 = 3). Жауап: 312.

3

2

1

(5 сурет)

Мультипликатор
Шотландтық математик Джон Напьер сандарды көбейтуге арналған 10 роликтен тұратын есептегіш құралды ойлап тапты. Құрылғы итальяндық сандарды көбейту қағидасына негізделеді.
Көп таңбалы санды бір таңбалы санға көбейту алгоритмін қарастырыңыз. Мысалға, сіз 258 · 8 өнімді есептеп шығарыңыз.
1 қадам. Таяқтарды алыңыз және бірінші қатарда нөмір жасаңыз. Біздің мысалда жолақтарды 2, 5 және 8-гі жоғарғы сандармен алып, келесіге қойыңыз
2 қадам. Сіз көбейту керек болғанда, көптеген жолдармен санауыңыз керек. Бұл мысалда сегізінші сызық.

3 қадам. Диагональды санаймыз, келесі жолға ондықты қосамыз.
Мысалда өнім 2064 болып табылады, 354 және 7 өнімнің басқа мысалы 7-суретте көрсетілген
«Naper's таяқшалары» бірнеше саннан тұратын сандарды көбейту үшін де пайдаланылуы мүмкін. «Математикалық қорап» кітабы осы әдісті түсіндіреді. Сіз екінші мультипликатордың әрбір санына көрсетілген алгоритмді орындауыңыз керек және нәтижелерді қосыңыз.
Өнімді 4375 · 347-ді есептеп алу қажет деп есептейік. Жоғарғы сандар 4 бар 4 жолақты қойыңыз; 3; 7; және 5. 4375 нөмірін 7-нің өнімін анықтаңыз. 30 625-ні алыңыз. 4375-ні 4-тен 4000-ға көбейтіп, 175000-ға жеткіземіз. Өнімді 4375-ден 3 жүзге дейін табамыз. Біз 13 125 жүз алады. Алынған жұмыстардың көлемін табу әлі қалады. 30 625 + 175000 + 1312500 = 1518 125.

Жеке көбейту құрылғысы
Жапондық әдіспен көбейту процесін модельдейтін екі таңбалы сандарды көбейту үшін өзімнің құрылғымды жасадым. Құрылғы келесідей көрінеді және ағаш жақтаудан және оған екі бағытта (тік және көлденең) резеңке таспалардан тұрады. Резеңке таспалардың жалпы саны 36:
18 тік;
18 көлденең.

Жапон көбейту әдісімен онымен жұмыс істеу оңай. Жақтаудың әр жағында 0-ден 9-ға дейінгі сандар жазылып, қиылысу сызығын есептеу үшін кішкене тесіктер жасалады. Оң жағында - бірліктер саны, жоғарғы жағы - ондық, сол жағы - жүздеген, ал төменгі жағы - келесі санға түсетін сан. Жапондық әдіспен көбейту кезінде, біз бірліктердің санын, содан кейін ондаған және жүздеген соңында есептеле бастаймыз.