
К.К.Есмуханова –БҚО,Ақжайық ауданы,Тайпақ орта жалпы білім беретін мектебі,жоғарғы санатты математика пәні мұғалімі
«Параметрлі теңдеулер мен теңсіздіктерді шешу»
Параметрі бар иррационал теңдеулер мен теңсіздіктерді шешу
Иррационал теңдеулерді шешудің негізгі тәсілі-анықталу облысын ескере отырып,радикалдан құтылу. Кейбір жағдайларда иррационал теңдеудің ерекшеліктерін пайдалынып басқа дәстүрлі емес шешімдерін табуға болады.
![]() ,теңдеуді екі рет квадраттап,сегізінші дәрежелі
көпмүшелік теңдеуге келтіруге болады,бірақ ондай теңдеуді шешу
қиындық туғызады. Сондықтан дәрежені төмендету тәсілін қолдансақ.Ол
үшін анықталу облысын табайық:
,теңдеуді екі рет квадраттап,сегізінші дәрежелі
көпмүшелік теңдеуге келтіруге болады,бірақ ондай теңдеуді шешу
қиындық туғызады. Сондықтан дәрежені төмендету тәсілін қолдансақ.Ол
үшін анықталу облысын табайық: 
Анықталу облысының ұштарындағы сандарды тексеріп
көрсек,![]() теңдеудің шешімі,ал
теңдеудің шешімі,ал
![]() теңдеуді қанағаттандырмайды.
теңдеуді қанағаттандырмайды.
1-тәсіл: толық квадратты
қолдану![]() =
= Бұдан
Бұдан ![]() немесе
немесе ![]() Бірінші теңдеуден
Бірінші теңдеуден ![]()
Екінші теңдеуден ![]() немесе 4x
немесе 4x![]() немесе
немесе
![]()
![]() немесе
немесе ![]() .Бұл сан теңдеудің анықталу облысына тиісті. Жауабы:
.Бұл сан теңдеудің анықталу облысына тиісті. Жауабы:
![]()
2-тәсіл: тригонометриялық
3-тәсіл:дәрежесін төмендету
4-тәсіл: күрделі радикалдар формуласын қолдану
5-тәсіл: параметр
енгізу![]()
![]() =a алмастыруын енгіземіз,
=a алмастыруын енгіземіз, 
Соңғы теңдеуден 
1+2x![]()
![]()
2. а-ның қандай мәнінде ![]() теңдеуінің неше түбірі бар?
теңдеуінің неше түбірі бар?
Анықталу облысы: ![]()
x-1=![]()
1.D<0
2.D=0![]()
3.D>0![]()
Жауабы: 1)![]() бір ғана түбірі бар 2)
бір ғана түбірі бар 2)![]() екі түбірі бар
екі түбірі бар
Теңдеуді шеш:
![]()
Шешуі: мұндай
теңдеулерді шешу үшін ![]() теңдеуін геометриялық тәсілмен шешуді қарастырайық.
Координаталық жазықтықта АВ=5 болатын екі нүкте
теңдеуін геометриялық тәсілмен шешуді қарастырайық.
Координаталық жазықтықта АВ=5 болатын екі нүкте
A(![]() берілсін. AC=
берілсін. AC=![]() болсын ,мұнда C(x;0 ) нүктесі. Біздің мақсатымыз х-ті табу.
Екі нүктенің арақашықтығының
болсын ,мұнда C(x;0 ) нүктесі. Біздің мақсатымыз х-ті табу.
Екі нүктенің арақашықтығының ![]() формуласы бойынша
формуласы бойынша 
 Нақтылық үшін
Нақтылық үшін
![]() болсын,онда AB=
болсын,онда AB=![]() теңдігі орындалуы үшін
теңдігі орындалуы үшін
![]() болуы қажет. Сонымен, A(
болуы қажет. Сонымен, A(![]()
І тәсіл: Координаталық жазықтықта
A(![]()
![]() ,C(x;0)
,C(x;0)
 AB=
AB=![]() ,яғни
,яғни
AX=X![]()
![]()
![]()
Олай болса, OX=OK-KX=2![]() -
-![]() немесе координаталық
немесе координаталық
тәсілмен
тапсақ: 
Жауабы:![]()
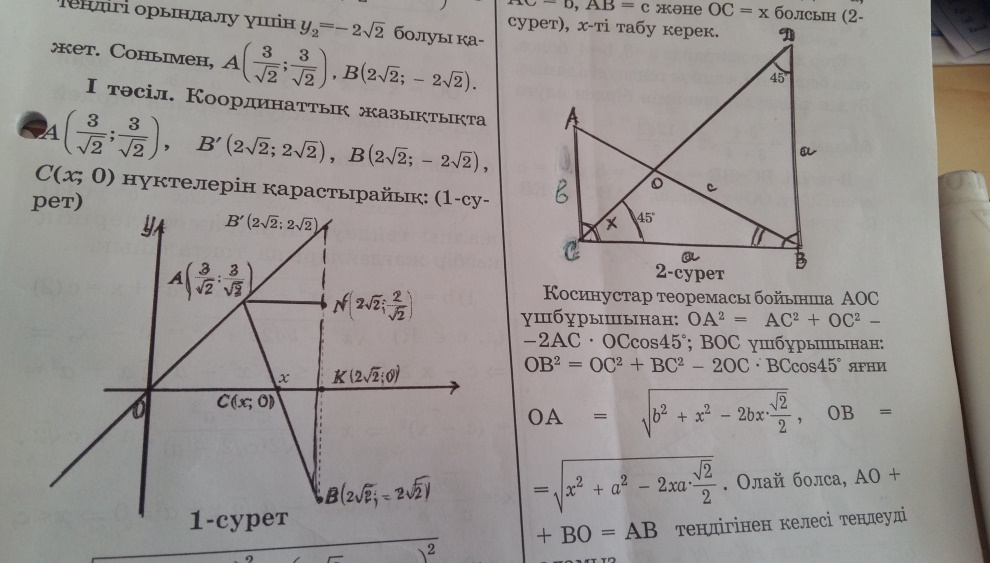
ІІ тәсіл: AC![]() және OC=x болсын х-ті табу керек
және OC=x болсын х-ті табу керек
Косинустар теоремасы бойынша АОС
үшбұрышынан: ![]()
ВОС үшбұрышынан: ![]() яғни )AO=
яғни )AO= ![]()
OB=![]() .Олай болса, AO+BO=AB теңдігінен келесі теңдеуді
аламыз
.Олай болса, AO+BO=AB теңдігінен келесі теңдеуді
аламыз
![]()
Осы теңдеуді шешейік: Мұндағы a,b,c>0,a,b,c![]() тек
тек ![]() болғанда ғана теңдеудің шешімі болады. Синустар теоремасы
бойынша
болғанда ғана теңдеудің шешімі болады. Синустар теоремасы
бойынша ![]()

мұндағы .Ал![]() мәндерін теңдеуге қойсақ :
мәндерін теңдеуге қойсақ :
![]() болғанда , x=
болғанда , x=![]() Сонымен теңдеудің жалпы шешімі: x=
Сонымен теңдеудің жалпы шешімі: x=![]()
Егер дербес жағдайда a=3,b=4 болса, онда
берілген алғашқы теңдеуді аламыз. Бұдан теңдеудің шешімін бірден
алуға болады. X=![]() =
=![]()
![]() =34 теңдеуінің а,в параметрінің қандай бүтін оң
мәндерінде бір түбірі болады.
=34 теңдеуінің а,в параметрінің қандай бүтін оң
мәндерінде бір түбірі болады.
Шешуі: ![]() Пифагор үштіктерінің формуласын пайдаланамыз. Ол үшін
c=34–ті жай көбейткіштерге жіктейміз.34=2(
Пифагор үштіктерінің формуласын пайдаланамыз. Ол үшін
c=34–ті жай көбейткіштерге жіктейміз.34=2(![]()
-18-
Осыдан,c=![]() ендеше,
ендеше,![]() Сонда
Сонда ![]() ,
,![]() Жауабы: a=16,b=30 және a=30,b=16
болса,теңдеудің түбірі болады.
Жауабы: a=16,b=30 және a=30,b=16
болса,теңдеудің түбірі болады.
Берілетін тапсырмалар:
![]() =65
=65
![]() =с
=с
3.![]() =13
=13
4.![]() =25
=25
5.![]() =с
=с
6.![]() =-7
=-7
Параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді шешу
-
 теңсіздігі барлық нақты х үшін орындалатындай
а нақты сандары табыла ма?
теңсіздігі барлық нақты х үшін орындалатындай
а нақты сандары табыла ма?
Шешуі: ![]()
![]()
![]() теңсіздік
теңсіздік ![]() түріне келеді ,мұнда
түріне келеді ,мұнда ![]() яғни
яғни
f(t)=![]() тармағы жоғары қараған парабола
тармағы жоғары қараған парабола ![]() теріс
мәнін қабылдауы керек:
теріс
мәнін қабылдауы керек: ![]() Шешімі жоқ
Шешімі жоқ
Жауабы: барлық кез келген х үшін теңсіздік орындалатындай а мәні табылмайды.
-
Қандай нақты а мәні үшін
 -(
-( теңдеуінің шешімі бар болады?
теңдеуінің шешімі бар болады?
Шешуі: sinx=t болсын,|sinx|![]() болғандықтан,
болғандықтан,![]() онда берілген теңдеу
онда берілген теңдеу ![]() түріне келеді, ал
түріне келеді, ал ![]() түбірлері [-1;1] кесіндісіне қатысты орналасуы әртүрлі
болуы мүмкін.
түбірлері [-1;1] кесіндісіне қатысты орналасуы әртүрлі
болуы мүмкін. ![]() үшмүшелігінің графигі тармағы жоғары қараған парабола және
шешімі бар болу үшін D=
үшмүшелігінің графигі тармағы жоғары қараған парабола және
шешімі бар болу үшін D=![]() болады. a) -1<
болады. a) -1<![]() болсын ,онда
болсын ,онда 
шешімі :![]()
b) -1<![]() болсын ,онда
болсын ,онда 
шешімі :![]()
г)![]() түбірлері [-1;1] кесіндісіне тиісті болсын,онда
түбірлері [-1;1] кесіндісіне тиісті болсын,онда

шешімі: -1![]()
d) 
шешімдерін біріктірсек. Жауабы:
![]()
3. Қандай нақты р үшін
![]() теңдеуінің шешімі бар болады?
теңдеуінің шешімі бар болады?
Шешімі: |sinx|![]() болғандықтан sinx=t, |t|
болғандықтан sinx=t, |t| ![]() алмастыруын орындайық:
алмастыруын орындайық:![]() Теңдеулердің
Теңдеулердің ![]() түбірлері [-1;1] кесіндісіне қатысты орналасулары әртүрлі
болуы мүмкін.
түбірлері [-1;1] кесіндісіне қатысты орналасулары әртүрлі
болуы мүмкін.
a) тармағы жоғары қараған параболаның
![]() түбірлері (-1;1) аралығында жатуы мүмкін,бұдан
есеп шартын қанағаттандыратын шарттарды жазайық:
түбірлері (-1;1) аралығында жатуы мүмкін,бұдан
есеп шартын қанағаттандыратын шарттарды жазайық:
 шешімі:-1
шешімі:-1![]()
Б)үлкен түбір ![]() ғана (-1;1) аралығында болуы мүмкін,ендеше
ғана (-1;1) аралығында болуы мүмкін,ендеше
![]() шешімі:1 < p < 2
шешімі:1 < p < 2
В) тек кіші ![]() түбірі ғана (-1;1) аралығында жатуы мүмкін,ендеше келесі
шарттар орындалады.
түбірі ғана (-1;1) аралығында жатуы мүмкін,ендеше келесі
шарттар орындалады.
![]() шешімі:-2 < p < -1
шешімі:-2 < p < -1
Г)үшмүшеліктің бір түбірі +1 немесе -1 –ге тең
болуы мүмкін. ![]() Болады,егер f(1)=0 ,яғни егер p=2 немесе p=-1 болса. Егер
p=1 немесе p=-2 болса,онда
Болады,егер f(1)=0 ,яғни егер p=2 немесе p=-1 болса. Егер
p=1 немесе p=-2 болса,онда ![]() =-1
=-1 ![]() Бұл төрт р мәндері есеп шартын қанағаттандырады.
Бұл төрт р мәндері есеп шартын қанағаттандырады.
Жауабы:![]()
Өз бетімен орындауға: ![]() кесіндісінде дәл үш түбірі болатындай
кесіндісінде дәл үш түбірі болатындай ![]() Ж; q=0;q=2;q=
Ж; q=0;q=2;q=![]()
Параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді шешу
-
теңдеуді шеш:

Дәрежені төмендету формуласын қолданамыз:
![]()
![]() болса,
болса,
-
2a-1=0

![]()
3.

4. a=1![]()
5.a>1![]()
![]()
Жауабы: ![]() a>1 болса,шешімі
жоқ
a>1 болса,шешімі
жоқ
![]()
y=sinx жаңа айнымалы
енгізсек,![]()
![]() болады,a=1
болады,a=1![]()
2.D=0![]()
a<0![]() егер a<0 немесе a>5 болса,теңдеудің шешімі
жоқ
егер a<0 немесе a>5 болса,теңдеудің шешімі
жоқ
![]() болса,теңдеудің екі шешімі
бар
болса,теңдеудің екі шешімі
бар![]() келесі теңсіздіктер дұрыс
болады:
келесі теңсіздіктер дұрыс
болады:![]()
Шындығында a=0
болса, ![]() a>0
a>0 ![]() >a-1
>a-1![]()
Егер a=0 болса,онда sinx=y теңдеуі sinx=-1
,x=![]()
Енді 

 соңғы жүйелерден
соңғы жүйелерден ![]()
![]() теңдеуінің
теңдеуінің ![]() ғана шешімі болады,ол.x=
ғана шешімі болады,ол.x=![]()
![]() болған жағдайда.
болған жағдайда.
Егер 4<a![]() онда теңдеудің шешімі жоқ.
онда теңдеудің шешімі жоқ.
Жауабы: ![]() ;
2)
;
2)![]() ,x=
,x=![]()
-
a<0; a>4 болса,теңдеудің шешімі жоқ
3. cos(a+x)=![]() теңдеуін шеш
теңдеуін шеш
Теңдеудің екі жағын cosx көбейтсек, cosx*cos(a+x)=cosa теңдеу аламыз.
![]()
![]() қиылыспайды
қиылыспайды 
![]() : 1)
: 1)![]() 2)
2)![]()
-22-
4.теңдеулер жүйесін шеш:
![]()
![]()

![]()

![]()

-
теңсіздігін шеш: tgx+ctgx

![]() ,
,![]()
![]() жағдайларын қарастырамыз.
жағдайларын қарастырамыз.
![]() 2)a>0
2)a>0 болғандықтан жағдайларын қарастырамыз:a)0<a<2 b)a=2 c)a>2
болғандықтан жағдайларын қарастырамыз:a)0<a<2 b)a=2 c)a>2
![]() 0<a<2
0<a<2![]()
![]()
![]() a>2
a>2![]()
3) a<0 a=-2
a=-2![]() жағдайларын қарастырамыз.
жағдайларын қарастырамыз.![]() a< - 2
a< - 2![]()
![]() a<0
a<0 ![]()
Қорытындды: ![]()
![]()
![]()
![]()
Сонымен ,y=sin2x болғанда,
алатынымыз: 1)егер a<-2 болса,онда
![]() ,одан
,одан

![]()
2)
егер -2![]() a< 2 болса,онда
a< 2 болса,онда
![]() ,одан 2
,одан 2![]()
3)
егер a=2
болса,онда ![]() ,одан
,одан ![]()
4)
егер a>2
болса,онда ![]() ,одан
,одан ![]()

Жауабы:1) егер a<-2 болса,онда
![]()
-23-
2)
егер -2![]() a< 2 болса,онда
a< 2 болса,онда
![]() ; 3) егер a=2
болса,онда
; 3) егер a=2
болса,онда ![]() ;4) егер a>2 болса,
;4) егер a>2 болса, ![]()
Қосымша берілетін тапсырмалар:
-
тапсырмалар
жауабы
cos2x-os4x=a*sinx
a<-2,a>2
 ;
;2

sin(x-a)=sinx+sina

a

12sinx+4

a<-8,a>8

-8

sin(x+a)+sinx=cos

a=

a

(a-1)cosx+(a+1)sinx=2a
a<0,a>1

0

sin(x+a)+cos(x+a)=sin(x-a)+cos(x-a)
a=

a

1+

a-рационал болса,

а-иррационал болса, 0
 =a
=a

|
|
|
-


a=-

a=

-

tgx+tga+1=ygx*tga
a=

 -a-
-a-
sin3x=a*sinx
a=-1

a=3

-1<a<3



a=

a>

cosx-

a<0


a=0

-

a>0

arccos

|
|
|
-

1.a<
 ; 2.
; 2. 
3.a>

Параметрі бар көрсеткіштік теңдеулер мен теңсіздіктерді шешу
1.а-ның қандай мәнінде
![]() теңдеуінің бір түбірі болады?
теңдеуінің бір түбірі болады?
![]()
Жауабы: ![]()
2.а-ның қандай мәндерінде
![]() теңcіздігі кех келген х үшін
орындалады?
теңcіздігі кех келген х үшін
орындалады?
Шешуі: ![]()
![]()
Жауабы: ![]()
3.![]()
Шешуі:
![]() )=0,D=1,
)=0,D=1,![]()
Жауабы: a<0,![]()
![]() теңдеуін шеш
теңдеуін шеш
Шешуі: 1. ![]()
![]()
Дискриминанты D![]()
![]()
1.a>0 болсын. Онда
,егер ![]() болса,x=
болса,x=![]() , ал, егер
, ал, егер ![]() болса,онда x=
болса,онда x=![]()
2. a<0 болсын.Онда ,егер
![]() болса, x=
болса, x=![]() ал егер
ал егер![]() болса,онда шешімі болмайды. Сонымен ,a>0
болса,онда
болса,онда шешімі болмайды. Сонымен ,a>0
болса,онда ![]() болса,онда шешімі жоқ; a<0 болса,онда
x=
болса,онда шешімі жоқ; a<0 болса,онда
x=![]() |a|
|a|
![]()
Параметрі бар логарифмдік теңдеулер мен теңсіздіктерді шешу
1.![]()
Белгілеу енгізсек:u=lg cosx![]()
1.D=![]()

3.D>0![]()
cosx=![]()
lg cos x ![]()

Lg cosx =-1+![]() шешім жоқ
шешім жоқ

![]() 1) егер
1) егер

2)![]()
3)егер -2<a<1![]() шешім жоқ
шешім жоқ
2.
1-ші теңдеуге қойып,түрлендірсек:
siny=![]()
siny>0 ![]()
cosx<![]()
егер a<0,a![]()
![]()
Қорытынды:
 болғанда ,жүйенің шешімі
болады.
болғанда ,жүйенің шешімі
болады.
![]()
![]()
![]() cosx+
cosx+![]() cosx+
cosx+![]()
 . Егер болса,онда соңғы
теңсіздік барлық х-тер үшін
орындалады.Сонымен ,берілген есеп келесі шарттармен
эквивалентті:
. Егер болса,онда соңғы
теңсіздік барлық х-тер үшін
орындалады.Сонымен ,берілген есеп келесі шарттармен
эквивалентті:
 Осыдан,
Осыдан,  } Демек,a
} Демек,a![]()
![]() а-ның барлық нақты мәндері үшін
шеш:
а-ның барлық нақты мәндері үшін
шеш:

![]() −ге тең болатын ерекше жағдайларды
қарастырайық:
−ге тең болатын ерекше жағдайларды
қарастырайық:
1.![]() .Онда
.Онда ![]() Осыдан x=0. Бірақ x=0 анықталу облысына
жатпайды.
Осыдан x=0. Бірақ x=0 анықталу облысына
жатпайды.
![]() Сондықтан ,егер
Сондықтан ,егер ![]() болса,онда теңдеудің шешімі x=1.
болса,онда теңдеудің шешімі x=1.
1.![]() . Бұл жағдайда логарифмдердің коэффициенттері 0-ден өзге
және оң болады. x
. Бұл жағдайда логарифмдердің коэффициенттері 0-ден өзге
және оң болады. x![]() болғанда 0<2x-
болғанда 0<2x-![]() және
және ![]() болатынын көру қиын емес.Егер 2x-
болатынын көру қиын емес.Егер 2x-![]() болса,онда x=1.Бірақ бұл жағдайда теңдік орындалмайды.
Сондықтан 0<2x-
болса,онда x=1.Бірақ бұл жағдайда теңдік орындалмайды.
Сондықтан 0<2x-![]() және
және ![]() нда
нда ![]() және
және ![]() Сонымен,бұл жағдайда теңдік орындалмайды.
Сонымен,бұл жағдайда теңдік орындалмайды.
Демек,егер a=![]() болса,онда теңдеудің шешімі x=1,ал егер
болса,онда теңдеудің шешімі x=1,ал егер
![]() болса,шешімі жоқ.
болса,шешімі жоқ.
5.теңдеулер жүйесінің шешімі болатын а-ның барлық мәндерін тап:


![]()
![]()
![]()
-
-
-

a<3,a>




-1<a



-
-
Қолданылған әдебиеттер тізімі:
-
В.Карасев ,и др. Решение задач с параметрами
-
М.Л.Галицкий и др.Сборник задач по алгебре,8-9 кл. М.2006
-
Л.И.Звавич ,А.Р.Рязановский Алгебра.Задачник.8 кл М.2004
-
Б.И.Александров и др. Пособие по математике для поступающих в ВУЗы.МГУ.1957 г.
-
В.Н.Литвиненко,А.Г.Мордкович «Практикум по элементарной математике Алгебра.Тригонометрия»,Москва «Просвещение»,1991
-
«Репетитор» , «ИФМ», «Математика және Физика» ғылыми-әдістемелік журналы
17
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Параметрлі теңдеулер мен теңсіздіктерді шешу /жалғасы/
Параметрлі теңдеулер мен теңсіздіктерді шешу /жалғасы/
К.К.Есмуханова –БҚО,Ақжайық ауданы,Тайпақ орта жалпы білім беретін мектебі,жоғарғы санатты математика пәні мұғалімі
«Параметрлі теңдеулер мен теңсіздіктерді шешу»
Параметрі бар иррационал теңдеулер мен теңсіздіктерді шешу
Иррационал теңдеулерді шешудің негізгі тәсілі-анықталу облысын ескере отырып,радикалдан құтылу. Кейбір жағдайларда иррационал теңдеудің ерекшеліктерін пайдалынып басқа дәстүрлі емес шешімдерін табуға болады.
![]() ,теңдеуді екі рет квадраттап,сегізінші дәрежелі
көпмүшелік теңдеуге келтіруге болады,бірақ ондай теңдеуді шешу
қиындық туғызады. Сондықтан дәрежені төмендету тәсілін қолдансақ.Ол
үшін анықталу облысын табайық:
,теңдеуді екі рет квадраттап,сегізінші дәрежелі
көпмүшелік теңдеуге келтіруге болады,бірақ ондай теңдеуді шешу
қиындық туғызады. Сондықтан дәрежені төмендету тәсілін қолдансақ.Ол
үшін анықталу облысын табайық: 
Анықталу облысының ұштарындағы сандарды тексеріп
көрсек,![]() теңдеудің шешімі,ал
теңдеудің шешімі,ал
![]() теңдеуді қанағаттандырмайды.
теңдеуді қанағаттандырмайды.
1-тәсіл: толық квадратты
қолдану![]() =
= Бұдан
Бұдан ![]() немесе
немесе ![]() Бірінші теңдеуден
Бірінші теңдеуден ![]()
Екінші теңдеуден ![]() немесе 4x
немесе 4x![]() немесе
немесе
![]()
![]() немесе
немесе ![]() .Бұл сан теңдеудің анықталу облысына тиісті. Жауабы:
.Бұл сан теңдеудің анықталу облысына тиісті. Жауабы:
![]()
2-тәсіл: тригонометриялық
3-тәсіл:дәрежесін төмендету
4-тәсіл: күрделі радикалдар формуласын қолдану
5-тәсіл: параметр
енгізу![]()
![]() =a алмастыруын енгіземіз,
=a алмастыруын енгіземіз, 
Соңғы теңдеуден 
1+2x![]()
![]()
2. а-ның қандай мәнінде ![]() теңдеуінің неше түбірі бар?
теңдеуінің неше түбірі бар?
Анықталу облысы: ![]()
x-1=![]()
1.D<0
2.D=0![]()
3.D>0![]()
Жауабы: 1)![]() бір ғана түбірі бар 2)
бір ғана түбірі бар 2)![]() екі түбірі бар
екі түбірі бар
Теңдеуді шеш:
![]()
Шешуі: мұндай
теңдеулерді шешу үшін ![]() теңдеуін геометриялық тәсілмен шешуді қарастырайық.
Координаталық жазықтықта АВ=5 болатын екі нүкте
теңдеуін геометриялық тәсілмен шешуді қарастырайық.
Координаталық жазықтықта АВ=5 болатын екі нүкте
A(![]() берілсін. AC=
берілсін. AC=![]() болсын ,мұнда C(x;0 ) нүктесі. Біздің мақсатымыз х-ті табу.
Екі нүктенің арақашықтығының
болсын ,мұнда C(x;0 ) нүктесі. Біздің мақсатымыз х-ті табу.
Екі нүктенің арақашықтығының ![]() формуласы бойынша
формуласы бойынша 
 Нақтылық үшін
Нақтылық үшін
![]() болсын,онда AB=
болсын,онда AB=![]() теңдігі орындалуы үшін
теңдігі орындалуы үшін
![]() болуы қажет. Сонымен, A(
болуы қажет. Сонымен, A(![]()
І тәсіл: Координаталық жазықтықта
A(![]()
![]() ,C(x;0)
,C(x;0)
 AB=
AB=![]() ,яғни
,яғни
AX=X![]()
![]()

![]()
Олай болса, OX=OK-KX=2![]() -
-![]() немесе координаталық
немесе координаталық
тәсілмен
тапсақ: 
Жауабы:![]()
ІІ тәсіл: AC![]() және OC=x болсын х-ті табу керек
және OC=x болсын х-ті табу керек
Косинустар теоремасы бойынша АОС
үшбұрышынан: ![]()
ВОС үшбұрышынан: ![]() яғни )AO=
яғни )AO= ![]()
OB=![]() .Олай болса, AO+BO=AB теңдігінен келесі теңдеуді
аламыз
.Олай болса, AO+BO=AB теңдігінен келесі теңдеуді
аламыз
![]()
Осы теңдеуді шешейік: Мұндағы a,b,c>0,a,b,c![]() тек
тек ![]() болғанда ғана теңдеудің шешімі болады. Синустар теоремасы
бойынша
болғанда ғана теңдеудің шешімі болады. Синустар теоремасы
бойынша ![]()

мұндағы .Ал![]() мәндерін теңдеуге қойсақ :
мәндерін теңдеуге қойсақ :
![]() болғанда , x=
болғанда , x=![]() Сонымен теңдеудің жалпы шешімі: x=
Сонымен теңдеудің жалпы шешімі: x=![]()
Егер дербес жағдайда a=3,b=4 болса, онда
берілген алғашқы теңдеуді аламыз. Бұдан теңдеудің шешімін бірден
алуға болады. X=![]() =
=![]()
![]() =34 теңдеуінің а,в параметрінің қандай бүтін оң
мәндерінде бір түбірі болады.
=34 теңдеуінің а,в параметрінің қандай бүтін оң
мәндерінде бір түбірі болады.
Шешуі: ![]() Пифагор үштіктерінің формуласын пайдаланамыз. Ол үшін
c=34–ті жай көбейткіштерге жіктейміз.34=2(
Пифагор үштіктерінің формуласын пайдаланамыз. Ол үшін
c=34–ті жай көбейткіштерге жіктейміз.34=2(![]()
-18-
Осыдан,c=![]() ендеше,
ендеше,![]() Сонда
Сонда ![]() ,
,![]() Жауабы: a=16,b=30 және a=30,b=16
болса,теңдеудің түбірі болады.
Жауабы: a=16,b=30 және a=30,b=16
болса,теңдеудің түбірі болады.
Берілетін тапсырмалар:
![]() =65
=65
![]() =с
=с
3.![]() =13
=13
4.![]() =25
=25
5.![]() =с
=с
6.![]() =-7
=-7
Параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді шешу
-
 теңсіздігі барлық нақты х үшін орындалатындай
а нақты сандары табыла ма?
теңсіздігі барлық нақты х үшін орындалатындай
а нақты сандары табыла ма?
Шешуі: ![]()
![]()
![]() теңсіздік
теңсіздік ![]() түріне келеді ,мұнда
түріне келеді ,мұнда ![]() яғни
яғни
f(t)=![]() тармағы жоғары қараған парабола
тармағы жоғары қараған парабола ![]() теріс
мәнін қабылдауы керек:
теріс
мәнін қабылдауы керек: ![]() Шешімі жоқ
Шешімі жоқ
Жауабы: барлық кез келген х үшін теңсіздік орындалатындай а мәні табылмайды.
-
Қандай нақты а мәні үшін
 -(
-( теңдеуінің шешімі бар болады?
теңдеуінің шешімі бар болады?
Шешуі: sinx=t болсын,|sinx|![]() болғандықтан,
болғандықтан,![]() онда берілген теңдеу
онда берілген теңдеу ![]() түріне келеді, ал
түріне келеді, ал ![]() түбірлері [-1;1] кесіндісіне қатысты орналасуы әртүрлі
болуы мүмкін.
түбірлері [-1;1] кесіндісіне қатысты орналасуы әртүрлі
болуы мүмкін. ![]() үшмүшелігінің графигі тармағы жоғары қараған парабола және
шешімі бар болу үшін D=
үшмүшелігінің графигі тармағы жоғары қараған парабола және
шешімі бар болу үшін D=![]() болады. a) -1<
болады. a) -1<![]() болсын ,онда
болсын ,онда 
шешімі :![]()
b) -1<![]() болсын ,онда
болсын ,онда 
шешімі :![]()
г)![]() түбірлері [-1;1] кесіндісіне тиісті болсын,онда
түбірлері [-1;1] кесіндісіне тиісті болсын,онда

шешімі: -1![]()
d) 
шешімдерін біріктірсек. Жауабы:
![]()
3. Қандай нақты р үшін
![]() теңдеуінің шешімі бар болады?
теңдеуінің шешімі бар болады?
Шешімі: |sinx|![]() болғандықтан sinx=t, |t|
болғандықтан sinx=t, |t| ![]() алмастыруын орындайық:
алмастыруын орындайық:![]() Теңдеулердің
Теңдеулердің ![]() түбірлері [-1;1] кесіндісіне қатысты орналасулары әртүрлі
болуы мүмкін.
түбірлері [-1;1] кесіндісіне қатысты орналасулары әртүрлі
болуы мүмкін.
a) тармағы жоғары қараған параболаның
![]() түбірлері (-1;1) аралығында жатуы мүмкін,бұдан
есеп шартын қанағаттандыратын шарттарды жазайық:
түбірлері (-1;1) аралығында жатуы мүмкін,бұдан
есеп шартын қанағаттандыратын шарттарды жазайық:
 шешімі:-1
шешімі:-1![]()
Б)үлкен түбір ![]() ғана (-1;1) аралығында болуы мүмкін,ендеше
ғана (-1;1) аралығында болуы мүмкін,ендеше
![]() шешімі:1 < p < 2
шешімі:1 < p < 2
В) тек кіші ![]() түбірі ғана (-1;1) аралығында жатуы мүмкін,ендеше келесі
шарттар орындалады.
түбірі ғана (-1;1) аралығында жатуы мүмкін,ендеше келесі
шарттар орындалады.
![]() шешімі:-2 < p < -1
шешімі:-2 < p < -1
Г)үшмүшеліктің бір түбірі +1 немесе -1 –ге тең
болуы мүмкін. ![]() Болады,егер f(1)=0 ,яғни егер p=2 немесе p=-1 болса. Егер
p=1 немесе p=-2 болса,онда
Болады,егер f(1)=0 ,яғни егер p=2 немесе p=-1 болса. Егер
p=1 немесе p=-2 болса,онда ![]() =-1
=-1 ![]() Бұл төрт р мәндері есеп шартын қанағаттандырады.
Бұл төрт р мәндері есеп шартын қанағаттандырады.
Жауабы:![]()
Өз бетімен орындауға: ![]() кесіндісінде дәл үш түбірі болатындай
кесіндісінде дәл үш түбірі болатындай ![]() Ж; q=0;q=2;q=
Ж; q=0;q=2;q=![]()
Параметрі бар тригонометриялық теңдеулер мен теңсіздіктерді шешу
-
теңдеуді шеш:

Дәрежені төмендету формуласын қолданамыз:
![]()
![]() болса,
болса,
-
2a-1=0

![]()
3.

4. a=1![]()
5.a>1![]()
![]()
Жауабы: ![]() a>1 болса,шешімі
жоқ
a>1 болса,шешімі
жоқ
![]()
y=sinx жаңа айнымалы
енгізсек,![]()
![]() болады,a=1
болады,a=1![]()
2.D=0![]()
a<0![]() егер a<0 немесе a>5 болса,теңдеудің шешімі
жоқ
егер a<0 немесе a>5 болса,теңдеудің шешімі
жоқ
![]() болса,теңдеудің екі шешімі
бар
болса,теңдеудің екі шешімі
бар![]() келесі теңсіздіктер дұрыс
болады:
келесі теңсіздіктер дұрыс
болады:![]()
Шындығында a=0
болса, ![]() a>0
a>0 ![]() >a-1
>a-1![]()
Егер a=0 болса,онда sinx=y теңдеуі sinx=-1
,x=![]()
Енді 

 соңғы жүйелерден
соңғы жүйелерден ![]()
![]() теңдеуінің
теңдеуінің ![]() ғана шешімі болады,ол.x=
ғана шешімі болады,ол.x=![]()
![]() болған жағдайда.
болған жағдайда.
Егер 4<a![]() онда теңдеудің шешімі жоқ.
онда теңдеудің шешімі жоқ.
Жауабы: ![]() ;
2)
;
2)![]() ,x=
,x=![]()
-
a<0; a>4 болса,теңдеудің шешімі жоқ
3. cos(a+x)=![]() теңдеуін шеш
теңдеуін шеш
Теңдеудің екі жағын cosx көбейтсек, cosx*cos(a+x)=cosa теңдеу аламыз.
![]()
![]() қиылыспайды
қиылыспайды 
![]() : 1)
: 1)![]() 2)
2)![]()
-22-
4.теңдеулер жүйесін шеш:
![]()
![]()

![]()

![]()

-
теңсіздігін шеш: tgx+ctgx

![]() ,
,![]()
![]() жағдайларын қарастырамыз.
жағдайларын қарастырамыз.
![]() 2)a>0
2)a>0 болғандықтан жағдайларын қарастырамыз:a)0<a<2 b)a=2 c)a>2
болғандықтан жағдайларын қарастырамыз:a)0<a<2 b)a=2 c)a>2
![]() 0<a<2
0<a<2![]()
![]()
![]() a>2
a>2![]()
3) a<0 a=-2
a=-2![]() жағдайларын қарастырамыз.
жағдайларын қарастырамыз.![]() a< - 2
a< - 2![]()
![]() a<0
a<0 ![]()
Қорытындды: ![]()
![]()
![]()
![]()
Сонымен ,y=sin2x болғанда,
алатынымыз: 1)егер a<-2 болса,онда
![]() ,одан
,одан

![]()
2)
егер -2![]() a< 2 болса,онда
a< 2 болса,онда
![]() ,одан 2
,одан 2![]()
3)
егер a=2
болса,онда ![]() ,одан
,одан ![]()
4)
егер a>2
болса,онда ![]() ,одан
,одан ![]()

Жауабы:1) егер a<-2 болса,онда
![]()
-23-
2)
егер -2![]() a< 2 болса,онда
a< 2 болса,онда
![]() ; 3) егер a=2
болса,онда
; 3) егер a=2
болса,онда ![]() ;4) егер a>2 болса,
;4) егер a>2 болса, ![]()
Қосымша берілетін тапсырмалар:
-
тапсырмалар
жауабы
cos2x-os4x=a*sinx
a<-2,a>2
 ;
;2

sin(x-a)=sinx+sina

a

12sinx+4

a<-8,a>8

-8

sin(x+a)+sinx=cos

a=

a

(a-1)cosx+(a+1)sinx=2a
a<0,a>1

0

sin(x+a)+cos(x+a)=sin(x-a)+cos(x-a)
a=

a

1+

a-рационал болса,

а-иррационал болса, 0
 =a
=a

|
|
|
-


a=-

a=

-

tgx+tga+1=ygx*tga
a=

 -a-
-a-
sin3x=a*sinx
a=-1

a=3

-1<a<3



a=

a>

cosx-

a<0


a=0

-

a>0

arccos

|
|
|
-

1.a<
 ; 2.
; 2. 
3.a>

Параметрі бар көрсеткіштік теңдеулер мен теңсіздіктерді шешу
1.а-ның қандай мәнінде
![]() теңдеуінің бір түбірі болады?
теңдеуінің бір түбірі болады?
![]()
Жауабы: ![]()
2.а-ның қандай мәндерінде
![]() теңcіздігі кех келген х үшін
орындалады?
теңcіздігі кех келген х үшін
орындалады?
Шешуі: ![]()
![]()
Жауабы: ![]()
3.![]()
Шешуі:
![]() )=0,D=1,
)=0,D=1,![]()
Жауабы: a<0,![]()
![]() теңдеуін шеш
теңдеуін шеш
Шешуі: 1. ![]()
![]()
Дискриминанты D![]()
![]()
1.a>0 болсын. Онда
,егер ![]() болса,x=
болса,x=![]() , ал, егер
, ал, егер ![]() болса,онда x=
болса,онда x=![]()
2. a<0 болсын.Онда ,егер
![]() болса, x=
болса, x=![]() ал егер
ал егер![]() болса,онда шешімі болмайды. Сонымен ,a>0
болса,онда
болса,онда шешімі болмайды. Сонымен ,a>0
болса,онда ![]() болса,онда шешімі жоқ; a<0 болса,онда
x=
болса,онда шешімі жоқ; a<0 болса,онда
x=![]() |a|
|a|
![]()
Параметрі бар логарифмдік теңдеулер мен теңсіздіктерді шешу
1.![]()
Белгілеу енгізсек:u=lg cosx![]()
1.D=![]()

3.D>0![]()
cosx=![]()
lg cos x ![]()

Lg cosx =-1+![]() шешім жоқ
шешім жоқ

![]() 1) егер
1) егер

2)![]()
3)егер -2<a<1![]() шешім жоқ
шешім жоқ
2.
1-ші теңдеуге қойып,түрлендірсек:
siny=![]()
siny>0 ![]()
cosx<![]()
егер a<0,a![]()
![]()
Қорытынды:
 болғанда ,жүйенің шешімі
болады.
болғанда ,жүйенің шешімі
болады.
![]()
![]()
![]() cosx+
cosx+![]() cosx+
cosx+![]()
 . Егер болса,онда соңғы
теңсіздік барлық х-тер үшін
орындалады.Сонымен ,берілген есеп келесі шарттармен
эквивалентті:
. Егер болса,онда соңғы
теңсіздік барлық х-тер үшін
орындалады.Сонымен ,берілген есеп келесі шарттармен
эквивалентті:
 Осыдан,
Осыдан,  } Демек,a
} Демек,a![]()
![]() а-ның барлық нақты мәндері үшін
шеш:
а-ның барлық нақты мәндері үшін
шеш:

![]() −ге тең болатын ерекше жағдайларды
қарастырайық:
−ге тең болатын ерекше жағдайларды
қарастырайық:
1.![]() .Онда
.Онда ![]() Осыдан x=0. Бірақ x=0 анықталу облысына
жатпайды.
Осыдан x=0. Бірақ x=0 анықталу облысына
жатпайды.
![]() Сондықтан ,егер
Сондықтан ,егер ![]() болса,онда теңдеудің шешімі x=1.
болса,онда теңдеудің шешімі x=1.
1.![]() . Бұл жағдайда логарифмдердің коэффициенттері 0-ден өзге
және оң болады. x
. Бұл жағдайда логарифмдердің коэффициенттері 0-ден өзге
және оң болады. x![]() болғанда 0<2x-
болғанда 0<2x-![]() және
және ![]() болатынын көру қиын емес.Егер 2x-
болатынын көру қиын емес.Егер 2x-![]() болса,онда x=1.Бірақ бұл жағдайда теңдік орындалмайды.
Сондықтан 0<2x-
болса,онда x=1.Бірақ бұл жағдайда теңдік орындалмайды.
Сондықтан 0<2x-![]() және
және ![]() нда
нда ![]() және
және ![]() Сонымен,бұл жағдайда теңдік орындалмайды.
Сонымен,бұл жағдайда теңдік орындалмайды.
Демек,егер a=![]() болса,онда теңдеудің шешімі x=1,ал егер
болса,онда теңдеудің шешімі x=1,ал егер
![]() болса,шешімі жоқ.
болса,шешімі жоқ.
5.теңдеулер жүйесінің шешімі болатын а-ның барлық мәндерін тап:


![]()
![]()
![]()
-
-
-

a<3,a>




-1<a



-
-
Қолданылған әдебиеттер тізімі:
-
В.Карасев ,и др. Решение задач с параметрами
-
М.Л.Галицкий и др.Сборник задач по алгебре,8-9 кл. М.2006
-
Л.И.Звавич ,А.Р.Рязановский Алгебра.Задачник.8 кл М.2004
-
Б.И.Александров и др. Пособие по математике для поступающих в ВУЗы.МГУ.1957 г.
-
В.Н.Литвиненко,А.Г.Мордкович «Практикум по элементарной математике Алгебра.Тригонометрия»,Москва «Просвещение»,1991
-
«Репетитор» , «ИФМ», «Математика және Физика» ғылыми-әдістемелік журналы
17

шағым қалдыра аласыз















