PISA ХАЛЫҚАРАЛЫҚ ЗЕРТТЕУІНІҢ ОҚУШЫЛАРДЫҢ ЛОГИКАЛЫҚ ОЙЛАУ, ФУНКЦИОНАЛДЫҚ САУАТТЫЛЫҚ АРТТЫРУДАҒЫ РӨЛІ

PISA ХАЛЫҚАРАЛЫҚ ЗЕРТТЕУІНІҢ ОҚУШЫЛАРДЫҢ ЛОГИКАЛЫҚ ОЙЛАУ, ФУНКЦИОНАЛДЫҚ САУАТТЫЛЫҚ АРТТЫРУДАҒЫ РӨЛІ

Абишева Айгуль Жарилгаповна

Атырау қаласы, Жалпы білім беретін С.Зиманов атындағы №37 орта мектебі

Математиканың басқа ғылыми пәндермен өзара байланыстарын іске асыру оқушылардың дүниетанымын дұрыс қалыптастыруға, табиғаттың құбылыстары мен процестерінің бірлігін сезінуге ықпал жасайды. Атап айтқанда, олар математикада материалдық әлемнің кеңістік формалары мен сандық қатынастарын бейнелей отырып, математика болмыстың математикалық модельдері туралы ғылым екендігін оқушылардың түсінуіне себептеседі.

«Сан», «фигура», «туынды», «интеграл», «вектор» ұғымдары реалды болмыстың саналуандылығын айқындайды, сондықтан да олар мектептегі басқа пәндердің қолданбалы есептерін шешуде кеңінен қолданылады. Табиғаттың көптеген заңдарын сипаттайтын сизықтық, квадраттық, логарифмдік, көрсеткіштік және т.б. функционалдық тәуелділіктер табиғатта байқалатын заңдылықтардың жалпылауы болып табылады.

Пәнаралық байланыстарды іске асыру барысында табиғат құбылыстарының біртұтастығы мен өзара байланыстарын көрсете отырып, оқушылардың білім мен білігін тереңдетуге қосымша мүмкіндіктер туады.

Мектеп математика оқулықтарында пәнаралық байланыстарды ашуға келтірілген нақты материалдар саны шектеулі, ал қосымша оқу әдебиеттерінен ондай материалды алып, сабақ барысында пайдалана қою - күрделі мәселе. Және де кезкелген дерлік мектеп пәнінің оқу бағдарламасы пәнаралық байланыстарды қосымша анықтау қажет болады.

Математика сабағында оқу тақырыптарын ашуға, оларды бекітуге, есеп шығартуға, республикамыздың экономикалық жетістіктері мен даму стратегиясын, ұлттық ерекшеліктерін, т.б. сипаттаушы материалдарды іріктеп таңдап алуға, оларды мазмұнына кірістіруге студент-болашақ математика пәнінің мұғалімін даярлау қажет. Себебі, мұндай мазмүндағы оқу-әдістемелік құралдар әзерге жоқ есебі

Пәнаралық байланыстарды іске асыру жолдары да жан-жақты. Атап айтсақ:

1) Математикалық ұғымдарды қалыптастыруда сол ұғымның мазмұнын ашу. Сабақтас пәндерде кездесетін ұғымды, мүмкіндігінше, бірмәнді түрде талқылау. Ал бір терминмен аталатын ұғымдардың мазмұндары әртүрлі болып келсе, онда оны оқушыларға (жас ерекшеліктеріне қарай) жете түсіндіру.

2) Математикалық ұғымдарды қалыптастырудағы басқа пәндердің материалдарымен, мәліметтерін қолдану.

3) Пәнаралық есептер және оларға қойылатын талаптар; математикалық модельдеу, абстракция, абстракциялаудың түрлері; т.б. сұрақтарды қарастыру.

4) Математика пәнін оқыту барысында оқушылардың логикалық ой-қабілетін дамыту.

5) Оқытылған материалдың күнделікті өмірдегі және сабақтас пәндердегі практикалық қолданыстарын көрсету.

Аспан, жер, су, тіпті, бізді айнала қоршаған әлемнің бәрінде де геометриялық объектілер толып жатыр. Былайша айтқанда, адам әрқашан да геометриялық әлемнің қоршауында. Салынған сарай - үйлер, жасалған кемелер, көкке ұшқан ұшақтар, күнде көретін ұсақ-түйек заттар - бәрі де геометриялық бейнелер арқылы танылады.

Планиметриядан стереометриялық ауысу кезеңінде оқушылардың санасында кеңістікті сезіну біртіндеп кеңиді. Кеңістікті сезінудегі айқынсыздық, тиянақсыздық оқушыларды X-XI сыныптардағы геометрия курсын толығымен түсінбеуіне әкеліп соғады.

Стереометрия курсының негізгі мақсаттарының бірі - кеңістіктегі қарапайым геометриялық бейнелердің қалыптасқан көріністерін тереңдету және кеңейту болып табылады. Жаңа күрделі ұғымдар иллюстрациялауды қажет етеді. Мысалы: түзу мен жазықтықтың арасындағы бұрыш, айқас түзулердің арасындағы бұрыш және оларға ортақ перпендикуляр, берілген екі жақты бұрыштың сызықтық бұрышы, дөңгелек денелер мен көпжақтар және т.б. Нақты мысал ретінде XI сыныпқа арналған геометрия оқулығындағы шардың анықтамасын қарастырайық: «Шар деп берілген нүктеден берілген қашықтықтан артық қашықтықта жататын кеңістіктің барлық нүктелерінен тұратын денені атайды. Бұл нүкте шардың центрі деп, ал берілген арақашықтық шардың радиусы деп аталады. Шардың шекарасы шардың беті немесе сфера деп аталады». [67, 325]. Бұдан оқушыларға беріліп жатқан ұғымдар турасында нақты түсінік алу қиынға соғуы мүмкін. Ал егер анықтаманы бермей тұрып, оқушыларға темірден құйылған шарды, ағаштан

жасалған шарды, допты, т.т. көрсетіп, ол заттардың әртүрлі қасиеттері бар екендігін еске түсірсек, мысалы, темірден жасалған шар - ток өткізеді, суға батады; ағаштан жасалған шар - ток өткізбейді, суға батпайды, т.т Шарлардың жасалған материалдарының тығыздықтары әртүрлі, түрлері де әртүсті, иістері де әртүрлі, т.т. қасиеттері бар. Бұл заттардың бәріне ортақ бір ғана қасиеті бар - олардың формалары. Енді біз тек сол қасиетті ғана - форманы - еске алсақ - «сфера», «шар» ұғымы шығады - деп, шардың анықтамасын қарапайым тілмен келтірсек, онда, біріншіден, оқулықтағы анықтаманы түсіну қиындыққа соқпайды, екіншіден, ұғымның өмірмен байланысын (абстракциядан пайда болғандығын) көрсетіп кетеміз.

Қабылданған аксиомаларға нақты өмірден мысалдар келтіріп, олардың қолданысын, практикаға қайшылықсыз екендігін көрсетіп отыру қажет. Мектеп стереометрия курсының мына теоремасын (ол негізінде Евклид геометриясының аксиомасы болатыны белгілі) алайық: «Берілген түзуде жатпайтын үш нүкте арқылы жазықтық жүргізуге болады және ол тек біреу ғана болады». Шынында да, үш аяқты орындық әрқашан орнықты тұрады. Ал төрт аяқты орындық болу үшін оның барлық аяқтарының ұзындықтары бірдей болуы қажет. Есік (жазықтықтың моделі) екі топсамен бекітілсе кеңістікте шексіз түрлі жағдайларда орналасады, ал егер оны қосымша бір жерінен тіресек (кілтпен, ілгекпен, таспен, т.т.) онда ол есік тек бір ғана жағдайда орналасады. Жоғарыда аталған аксиоманың іс жүсінде орынды болып отырғанын көреміз.

Тәжірибе көрсеткеніндей, 10-11 сыныптарда көрнекі құралдарды қолдану оқушылардың ойлау қабілетінің жас ерекшеліктерін және жеке-дара ерекшеліктерін айрықша еске алып отыруды қажет етеді: кейбір модельдеге тек сілтеме беруге болады, ал басқа ұғымдарды анықтағанда эскиз немесе суретпен шектелуге болады; кейбір модельдерді тек нақты ойлауы басым болып келетін оқушылардың арнайы тобында ғана қолдануға болады. Кеңістіктегі түзулер мен жазықтықтардың параллельдігін немесе перпендикулярлығын, екіжақты және көпжақты бұрыштарды оқытқанда көрнекі модельдердің аса маңыздылығын мектептегі жұмыс практикасы көрсетіп жүр.

Берілген фигураны дұрыс елестету, сызбаны дұрыс орындау үшін оқушылар алдымен кеңістіктегі фигураларды жазықтықта шартты түрде бейнелеудің негізгі талаптарын білулері қажет. Мұндай ережелер оқушылар үшін жазық емес фигураның сызбасын орындаудың бағыттық негізі болып табылады. Жоғары сынып оқушыларын бұл ережелер және әдістер мен геометриялық фигуралардың дербес түрлерін оқыту барысында бірте-бірте таныстыру керек. Бұл кезде параллель проекциялаудың қасиеттеріне және оқушылардың сызба курсында алған білімдері мен біліктеріне сүйеніп отыру қажет.

Негізінде фигураның параллель проекциясы туралы түсінікті қалыптастыру үшін шуақты күні сол фигураның картоннан немесе сымнан жасалған моделінің көлеңкесін қарастыруға болады. Күннің Жерден өте алыс қашықтықта екенін ескере отырып, Күн сәулелерін жуықтап өзара параллель деуге болады.

Кеңістіктегі фигураның кескінінің көрнекілігі сол фигураның проекциялау жазықтығына және проекциялай бағытына қатысты орналасуына тәуелді екені белгілі.

Үшбұрыштың моделінің көлеңкесін бақылай отырып, проекциялау жазықтығына қарағанда түп нұсқаның әртүрлі орналасуы арқылы берілген үшбұрыштың проекциясы кезкелген формадағы үшбұрыш (тіпті кесінді) болуы мүмкін деген ұйғарымға келеміз.

Кеңістіктегі түзулер мен жазықтықтардың параллельдігін және перпендикулярлығын, екіжақты және көпжақты бұрыштарды оқытқанда картоннан, органикалык шыныдан жасалған көрнекі модельдерді қолдану маңызды.

Жоғары сыныптарда геометрияны оқутыдан бастап көпжақтар ұғымы енгізіледі (параллелепипед, призма, пирамида, дұрыс көпжақтар). Бұл бірінші жағынан, параллельдік пен перпендикулярлықтың қасиеттерін көпжақтар негізінде көрсетуге мүмкіндік береді, екінші жағынан, оқушылардың геометриялық шамаларды, қалыптастыруға мүмкіндік жасайды.

Геометриялық денелердің көлемін табуды қарастырғанда, егер дене геометриялық формасых болса, онда көлемін

табу есебі математикалық әдіспен шешілмейді, ал физикада мензурканың көмегімен Архимед заңына сүйеніп шығаруға болады.

10-11 сынып оқушылары есептің шарты бойынша «пирамида берілді» десе үшбұрышты немесе төртбұрышты пирамиданы сызады, себебі пирамиданың бұл екі түрі стандартты сызбаларда жиірек кездеседі. Сондықтан әртүрлі дұрыс және емес, табан қабырғаларының саны әртүрлі болатын көпжақтарды бейнелеуді мұғалім өз практикасына еңгізсе, бұл кеңістіктегі фигура туралы абстрактілі ұғымды дұрыс қалыптастыру ықпал етеді.

Айналамыздағы бізді қоршап тұрған нәрселер геометриялық денелер туралы түсінік береді. Мысалы, кристалдар - көпбұрыштардан тұратын геометриялық денелердің пішінін береді. Ондай беттерді көпжақтар дейді.

Табиғи көпжақтар табиғаттағы геометрияның бір айқын көрінісі. Кристалл - қырлы біртекті қатты дене. Гректің «кристаллос» сөзі «мұз» деген ұғымды білдіреді. Бірақ бұл сөз тек қатқан мұздың кристалдарына ғана тән емес. Барлық тас, тау жыныстарыны көбі кристалдан тұрады. Металл рудалары, осы рудадан балқытып алынған металдың өзі, тұз, қант және айналамыздағы басқа да толып жатқан нәрселердің көбі кристалды заттар. Кристалдардың ішіндегі ең әдемісі - асыл тастар.

Кристалдардың ерекше қасиеті бар, мұның өзі олардың қандай атомдардан тұратындығына байланысты. Кристалдардың ішкі әлемін рентген сәулесі арқылы зерттеуге болады. Сонда, кристалдағы әрбір атом іргелес атомдардың нақты бір санымен байланысты болады және олар сонымен қосы белгілі ретпен орналасады екен. Әрбір кристалл формасы болады.

Кейбір заттардың бір емес, екі, үш, тіпті одан да көп кристалдық форма түзетіні кездеседі. Әрине, олардың бәрі де белгілі бір нақты тәртіппен орналасады. Мәселен, көміртегі осындай. Атомдардың орналасуына қарай, ол не алмасқа - жер бетіндегі ең әдемі, ең мөлдір, ең қатты тасқа, не кәдімгі қарындаштағы қара сұр түсті жұмсақ графитке айналады

Кристалдардың басқа да қасиеттері бар. Кристалдың ұзыны мен көлденеңінен жылу біркелкі өтпейді. Кыздырған кезде ол әр бағытта, әр түрлі ұлғаяды.

Көпжақтардың көптеген формаларын (тау хрусталі, алмаз. гранит, т.б.) кристалдар түрінде табиғат өзі жаратқан (28-сурет).

Табиғи кристалдардың арасында тетраэдрдың, октаэдрдың, кубтың, додекаэдрдың формалары айқындалған.

Кристалдардан көптеген қажетті заттар жасайды. Қазіргі кезде дұрыс көпжақтардың формалары архитектурада, тұрмыстық заттарда да кеңінен қолданылады. Мәселен, жартылай өткізгіш кристалдар радиотехникада қолданылады. Сағат тасы да - кристалл. Кристалдың бұдан басқа да қолданылатын жері өте көп.

Мысал-1. Параболаның теңдеуі

Суреттегі көпірді модельдейік.

y=- +

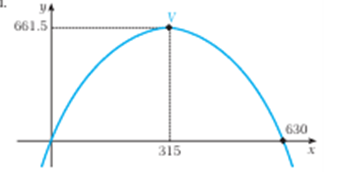
1-сурет.

а) Арқа теңдеуінің сызбасын координат осіне салыңыз.

б) Арқа бір жағынан екіншісіне дейінгі қашықтық қандай?

Шешуі:

a.

V(315,661,5)

x=0;y=0 (0;0) және (630;0) нүктелері x-осімен қиылысады.

b. x-осімен қиылысу нүктелерін пайдаланып,көпірдің ұзындығын табуға болады - 630 m.

Мысал-2. Пифагор теоремасы

Ұзындығы 5 м болатын баспалдақ үйдің жанынан салынған, баспалдақтың көлеңкесінің ұзындығы жерден баспалдаққа дейінгі ара қашықтықтан 1 м-ге кем. Баспалдақтың проекциясының ұзындығын есептеңіз.

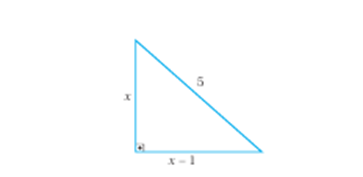
2-сурет.

Шешуі: Айталық, х-жерден баспалдыққа дейінгі ара қашықтық болса, онда проекциясының ұзындығы х-1 м. Суретте көрсетілгендей баспалдақтың орналасуынан тік бұрышты үшбұрышты көруге болады. Пифагор теоремасын қолдану арқылы есептейміз:

(x+3)(x-4)=0

Теңдеудің түбірі (-3) шешімі бола алмайды, себебі, теріс сан ұзындық өлшемі бола алмайды, ал x=4 – жерден баспалдақтың ұшына дейінгі ара қашықтықты береді. Ал баспалдақ проекциясының ұзындығы 3 м болады.

Мысал-3. Физика+Бильярд ойыны+Геометрия.

Ойыншының мақсаты битоктың неғұрлым жиірек керек жерден табылуына ықпал ету . Яғни сіз оның соққыдан кейін қайда домалайтынын қадағалауыңыз керек.

Бір қарағанда соққының аты соққы сіз қай жақтан соғуды таңдайтындай ғана болып көрінесіз. Алайда, кий ұшының ауданы өте кішкентай ал шар едәуір үлкен. Оны дәл ортаны көздеп немесе ойынды қыздыра түсу үшін сәл жылжыған бағытты таңдаумен соғуғу болады. Бильярдшылардың барлығы тоғыз нүктені ерекшелейді шардың қозғалысы соларға тигізуге байланысты.

Міне осы жерде физика іске араласады. Егер шарды тура ортасынан соқса ол қатаң түрде алға қарай қозғалып кедергіге кездесіп тоқтайды. Ал кийдің бір жаққа қарай жылжытқанда шар сол жаққа қарай қосымша айналады .

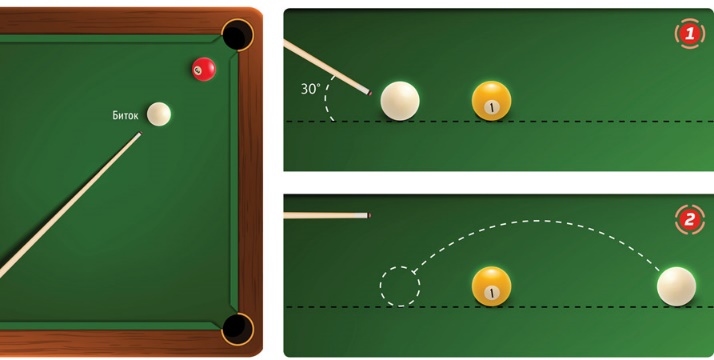
3-сурет

Егер біз 6 нүктесін соғар болсақ, шар алға қарай домалайды, бірақ көлденең өсінің айналасында кері бағытта айналады .Ол кедергіге кездескен кезде алға итеретін негізгі қозғалыс импульсі жоғалып, қалған қосымша айналу есебінен шар аздап артқа сырғиды .Оңға немесе солға соғу оны сәйкес жағына қарай айналдырады.

Егер битокты төмен қарай 30 градус бұрыштап қрса шар үстелден өтіп, ұшады .Осылайша кедергілерден секіріп өтуге болады. Соққы бүйір тұсқа қарай жылжытпай берілгендіктен үстелге оралғаннан кейін шар түзу бойымен домалайды. Мұндай соққыны көбінесе бильярд тәсілдері шыңдалған шеберлер қолданады, бірақ әдеттегі ойындарда да қолданылуы әбден мүмкін.

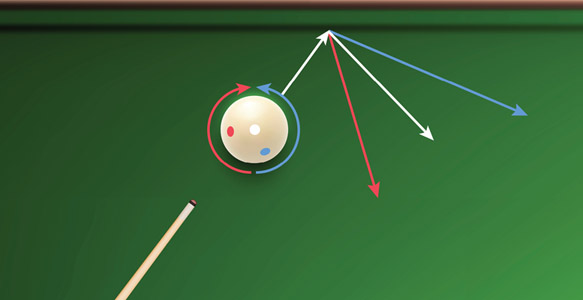
4-сурет

Бильярд үстелі шексіз емес, сондықтан шарлар бір біріне соғылуымен қатар үстелдің жақтауына да тиіп жатады. Шарлардың бұл жағдайдағы әрекеті жайлы физика не дейді ?

Мектеп қабырғасынан жақсы білетіндей ,түсу бұрышы шағылу бұрышына тең болады .Күн сәулесінің айнаға шағылысы секілді тік ұшқан шар үстел жақтауынан кері серпіледі .Ал шар оңға немесе солға бұрылған болса жақтауға соғылған кезде ол қосымша айналымға ие болып траекториясын бұзады. Оңға қарай бұрылған шар суретте қызыл траектория жақтауға жақын барады, солға бұрылған шар көк кеңірек бұрышпен домалайды.

Мысал-1.Дыбысзорайтқыштар

ЕСЕП

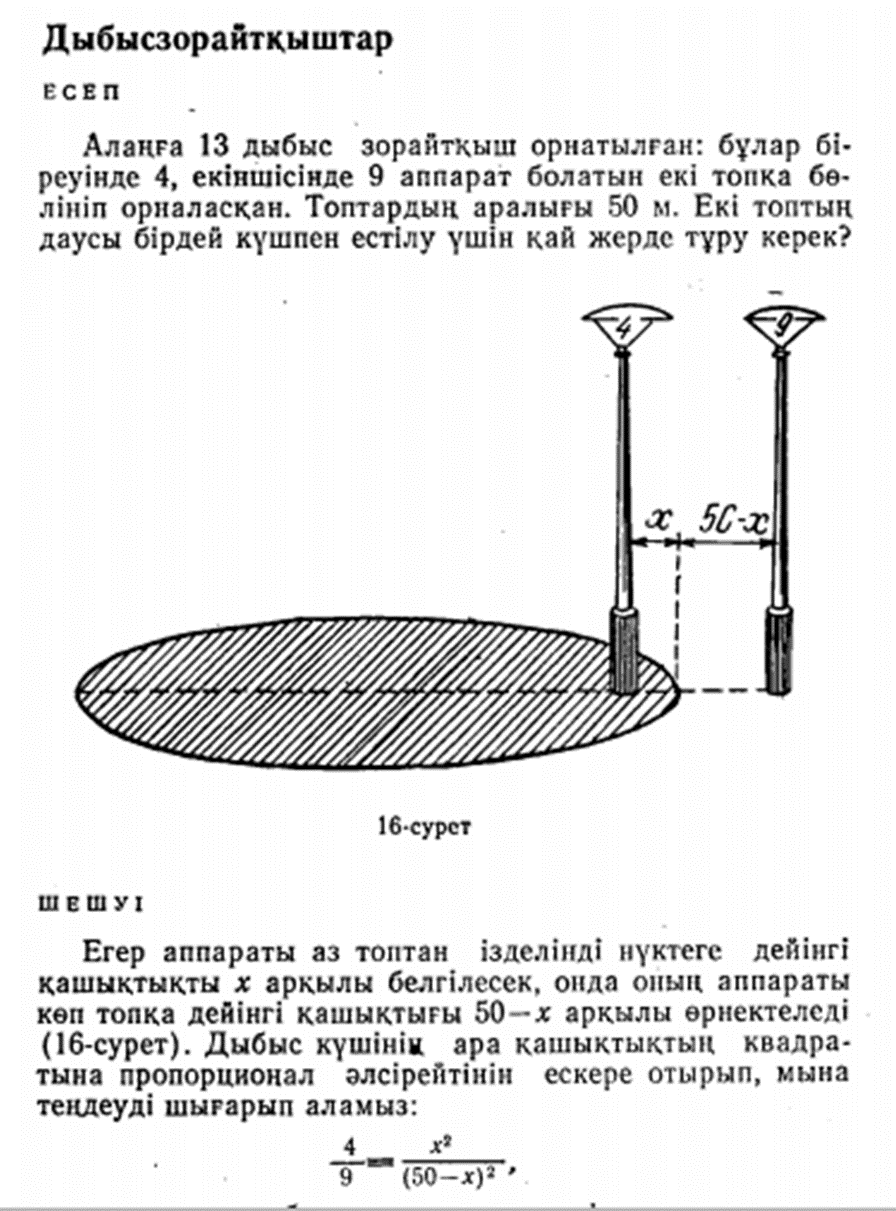
Алаңға 13 дыбыс зорайтқыш орнатылған: бұлар біреуінде, екіншісінде 9 аппарат болатын екі топқа бөлініп орналасқан. Топтардың аралығы 50 м. Екі топтың даусы бірдей күшпен естілу үшін қай жерде тұру керек?

5-сурет

ШЕШУІ

Егер аппараты аз топтан ізделінді нүктеге дейінгі қашықтықты х арқылы белгілесек, онда оның аппараты көп топқа дейінгі қашықтығы 50-х арқылы өрнектеледі (16-сурет). Дыбыс күшінің ара қашықтықтың квадратына пропорционал әлсірейтінін ескере отырып, мына теңдеуді шығарып аламыз:

ықшамдаған соң бұл мына түрге келеді:

,

Мұны шешіп, екі түбір табамыз:

Оң түбір есептің сұрауына тікелей жауап береді: дауыс бірдей естілетін нүкте төрт дыбысзорайтқыштан тұратын топтан 20 м қашықтықта, сондықтан тоғыз аппараттан тұратын топтан 30 м қашықтықта орналасқан.

Теңдеудің теріс түбірі нені білдіреді? Оның мағынасы бар ма?

Сөзсіз мағынасы бар. Минус таңбасы дауыс бірдей естілетін екінші нүктенің теңдеу құру кезінде оң деп қабылданған бағытқа қарама-қарсы бағытта жататынын білдіреді.

Төрт аппарат орналасқан жерден қажетті бағытта 100 м өлшеп дыбысзорайтқыштардың екі тобынан дауыстың бірдей күшпен естілетін нүктесін табамыз. Бұл нүкте тоғыз аппараттан тұратын топтан 100 м +50 м =150 м қашықтықта жатады.

Сонымен біз дыбыс шығатын көздердің арасын қосатын түзудің бойында жататын, дыбыс бірдей күшпен естілетін екі нүктені іздеп таптық. Бұл түзудің бойында басқа мұндай нүктелер жоқ, бірақ ондай нүктелер ол түзуден тысқары жерлерде бар. Біздің есебіміздің талабын қанағаттандыратын нүктелер жиыны сол табылған екі нүктені диаметрінің екі ұшы ретінде алып жүргізілген шеңбер екенін дәлелдеуге болады. Бұл шеңбер едәуір аймақты (суретте шрихталып көрсетілген) қоршап жатады, мұның , ішінде төрт дыбысзорайтқыштан тұратын топтың дауысынан күштірек естіледі, ал бұл шеңберден тысқары жерде бұған кері құбылыс байқалады.

Мысал-2.Фотосуретте иррационал санның қолданылуы

Фотографтарда √2 нөмірін қолдануға себеп бар. R радиосы бар шеңберді қарастырыңыз. Оның аумағы πR². Егер біз аймақты екі есе құрғымыз келсе, радиустың қай санымен көбейтілу керек деп ойлайсыз? Ал жартысы қанша болса - қалай бөлуге болады? Тағы да біз √2 санымен танысамыз.

6-сурет

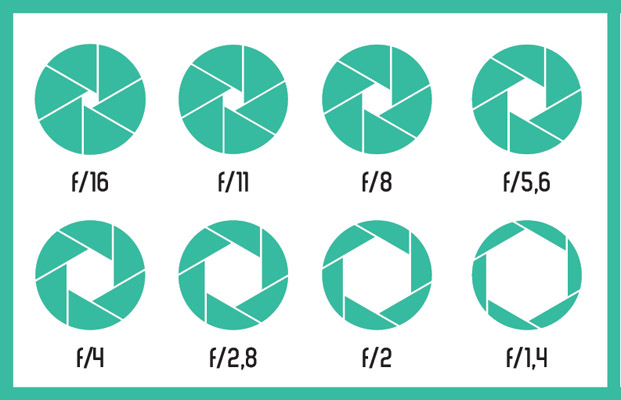
Бұл суретке қалай қатысты? Қолмен жұмыс режимінде түсіргенде, біз фокусты және экспозицияны реттей аламыз. Соңғысы люстра жылдамдығы мен линзаның диафрагмасы арқылы анықталады - линзалар арқылы жарық ағыны пленка немесе камераның матрицасына реттеуге мүмкіндік беретін айнымалы радиусы тесік. Егер жарық жарқын болса, раманы жарықтандырмау үшін диафрагма тесіктері азаяды. Егер жарық төмен болса - бұл күндіз немесе тіпті түнде - диафрагма ашылуы артады, әйтпесе жақтау тым қараңғы болады. Диафрагманың өлшемдері тұрақты мәнге ие: бір бөлікпен жабылған кезде, тесік аймағы екі есе, радиусы тиісінше √2 рет. Диафрагтық шкала бойынша бөлімшелер диафрагманың санына сәйкес келеді: 2; 2.8; 4; 5.6; 8; 11; 16; 22 және т.б. Үлгі айқын емес, бірақ іс жүзінде бұл √2 (кейбір себептермен математикалық заңдарға сəйкес емес дөңгелектенген) өкілеттіктерінің шамаланған мəні ғана емес:

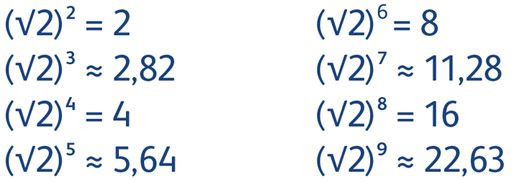
7-сурет

Өйткені, егер алдыңғы бөлігіндегі жартысы бар аймақты қамтитын топтар топтамасын алу керек болса, онда біз түпнұсқа шеңбердің радиусын √2 арқылы бөліп отыруымыз керек. Осылайша, осы сериядан алынған екі еркін шеңбердің радиусы әрқашан √2 қуатына тең болады.

ПРАКТИКАЛЫҚ ТАПСЫРМА

Quizizz

Викториналар, тестілер мен сауалнамалар жасауға арналған Quizizz қызметі ақысыз. Бұл құралдың көмегімен сіз:

-ойындар, тестілер, сауалнамалар мен викториналар өткізу;

-жарыстар ұйымдастырады;

-әр оқушының нәтижесін қадағалау;

-студенттер арасында жарыстар ұйымдастырыңыз.

Алдын ала жұмыс жасаңыз: сұрақтар мен жауаптары бар тапсырмалар тізімін жасаңыз. Викторинаның нұсқаларын жазыңыз. Сервис мыналарды жасауға мүмкіндік береді:

-бірнеше нұсқадағы бір дұрыс жауабы бар сұрақтар;

-жауаптардың бірнеше таңдауымен;

-ашық сұрақтар;

-шағын очерктерге өріс құру;

-сауалнамалар жүргізу;

-қызметті Google Classroom қызметіне қосу.

Quizizz қызметін ашыңыз. Google тіркелгісі немесе электрондық пошта арқылы тіркеліңіз (жоғарғы оң жақ бұрыштағы тіркеу батырмасы немесе «Бастау» батырмасын басыңыз). Тіркелгеннен кейін сізден қызметті қалай пайдаланатындығыңыз сұралады: мұғалім ретінде, студент ретінде, бизнес үшін немесе ата-ана ретінде.

S- «күшті жақтары»	W- «әлсіз тұстары»
Ашық және жабық сұрақтар арқылы оқушылармен үй жұмысын, теориялық материалды оңай тексеру,қалыптастырушы бағалау тапсырмаларын тиімді ұйымдастыру құралы.	Ұялы телефонның әр оқушыда болуын қажет етеді.
O- «мүмкіндіктері»	T- «қатерлі тұстары»
Оқу 770 ₸ - Сатып алу Материал ұнаса әріптестеріңізбен бөлісіңіз Ватсапта бөлісу Телеграммда бөлісу Фейсбукта бөлісу Сілтемені көшіру Ашық сабақ, ҚМЖ, көрнекілік, презентация жариялап табыс табыңыз! Материалдарыңызды сатып, ақша табыңыз. (kaspi Gold, Halyk bank) Соңғы бір жылда: 45 000 000 ₸ Авторлар тапқан ақша Толығырақ Ресми байқаулар тізімі Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз! Тізімді көру Материал іздеу Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде пәніңізді белгілеп, керек материалды алып сабағыңызға қолдана аласыз Барлығы 663 959 материал жиналған Пән Жүктелуде... Бағыт Жүктелуде... Сынып Жүктелуде... Іздеу Осы аптаның ең үздік материалдары Педагогтардың біліктілігін арттыру курстары Аттестацияда (ПББ) 100% келетін тақырыптармен дайындаймыз Аттестацияда (ПББ) келетін тақырыптар бойынша жасалған тесттермен дайындалып, бізбен бірге тестілеуден оңай өтесіз Өткен жылы бізбен дайындалған ұстаздар 50/50 жинап рекорд жасады Толығырақ