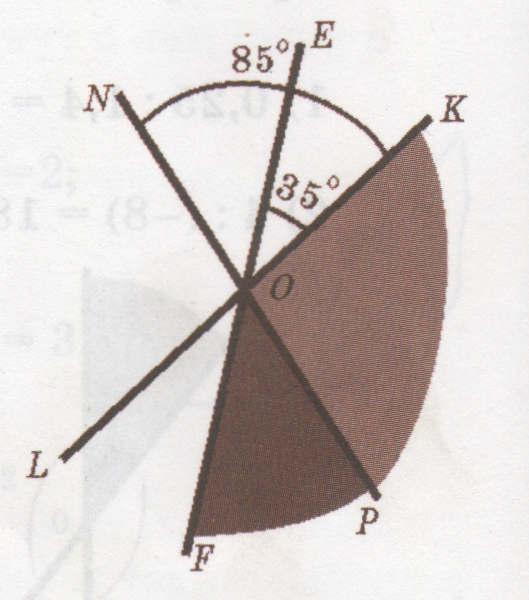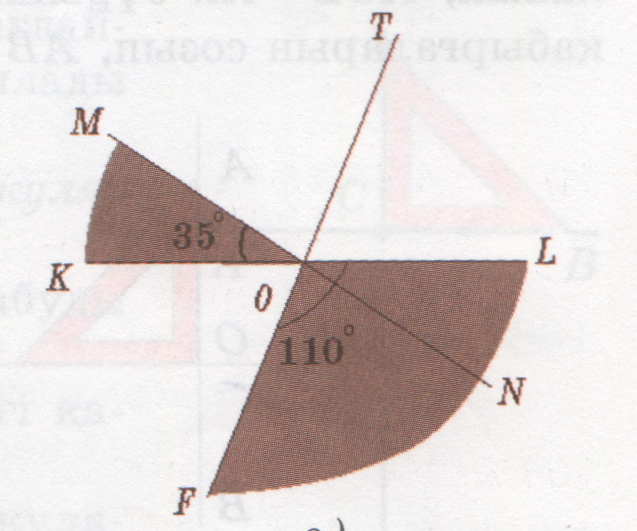Сабақтың тақырыбы:
Қиылысатын түзулер
Сабақтың мақсаты:
а)білімділік:Оқушылардың түзулер жайлы білімдерін
толықтыру, қиылысатын түзулерді түсіндіру ;
ә)дамытушылық:
түзулер туралы білімдерін
дамыту;
б)тәрбиелік:ұқыптылыққа,дәлдікке
үйрету;
Көрнекілігі:
оқулық, сызғыш,
қарындаш.
Әдісі: түсіндіру
Түрі: жаңа сабақ
Сабақтың барысы:
I. Ұйымдастыру
кезеңі:
а) сәлемдесу;
ә) оқушылардың сабаққа қатысын
тексеру;
б) оқушы зейінін сабаққа
аудару;
II. Үй тапсырмасын
сұрау: №1035
III. Жан – жақты білімдерін
тексеру:
1. Санды теңсіздік деген
не?
2. Координаталық түзуде үлкен сан кіші санның
қай жағында кескінделеді?
3.Санды теңсіздіктегі қосылғышты оның бір жақ
бөлігінен екінші жақ бөлігіне қалай көшіруге
болады?
IV. Жаңа сабаққа
кіріспе:Оқушылардың жаңа сабаққа дайындығын қадағалау.
Қызығушылығын ояту. Ребус шешу.
V. Жаңа
сабақ:Жазықтықта А және В екі нүкте белгілеп, оларды
сызғышпен қоссақ, АВ кесіндісі сызылады. АВкесіндісін сызғыштың
көмегімен екі жағынада созып,АВ түзуін саламыз. Сонда жазықтықтағы
А және В екі нүкте арқылы бір ғана АВ түзуі жүргізіледі. Түзу –
шектеусіз фигура.
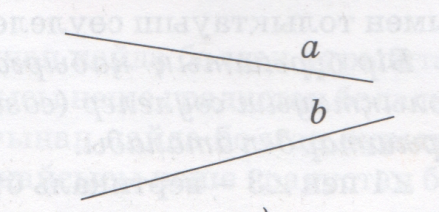

Бір түзуді екі үлкен латын әрпімен белгілеуді
білеміз. Түзу бір кіші латын (a,b,s,t,…) әрпімен де
белгіленеді.
Қиылысатын екі түзудің ортақ бір ғана нүктесі
болады.
а түзуі мен b түзуі – қиылысушы түзулер. О –
қиылысу нүктесі.
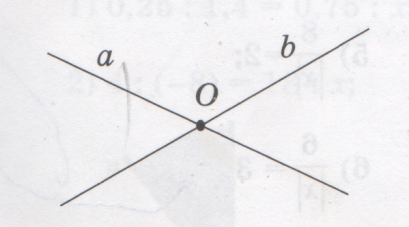
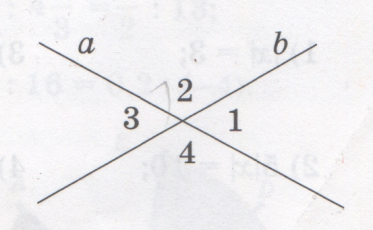
Жазықтықтағы екі түзудің қиылысуынан (жазыңқы
бұрыштарды есептемегенде) төбелері ортақ төрт бұрыш пайда болады.
Егер a және b түзулерінің қиылысуынан пайда болған бұрыштардың
біреуінің градустық өлшемі белгілі болса, қалған бұрыштардың
градустық өлшемдерін табуға болады.
Мысалы, 
<2,<3 және <4 – тың градустық
өлшемдерін табайық.
 және <2 бір жазыңқы бұрышты
құрайды.
және <2 бір жазыңқы бұрышты
құрайды.
<1+<2= , осыдан <2=
, осыдан <2=
<2+<3=  , осыдан<3=
, осыдан<3=
<3+<4= осыдан<4=
осыдан<4=
Есептеулерден <1 және <2=<4. Мұндағы <1 және
және <2=<4. Мұндағы <1 және
 тың, сол сияқты <2 және <4 –
тың біреуінің қабырғалары екіншісінің қабырғаларымен толықтауыш
сәулелер.
тың, сол сияқты <2 және <4 –
тың біреуінің қабырғалары екіншісінің қабырғаларымен толықтауыш
сәулелер.
Бір бұрыштың қабырғалары, екінші бұрыштың
қабырғаларымен толықтауыш сәулере болатын екі бұрыш вертикаль
бұрыштар деп аталады.
<1 және  вертикаль бұрыштар,
<2 және <4 – вертикаль бұрыштар.
вертикаль бұрыштар,
<2 және <4 – вертикаль бұрыштар.
Вертикаль бұрыштар өзара
тең.
Екі түзу қиылысқанда пайда болатын вертикаль
бұрыштардың бір жұбы сүйір бұрыштар болса, екінші жұбы доғал
бұрыштар болады.
VI. Жаңа сабақты түсінгенін
тексеру:
1.Қиылысатын түзулер қалай
сипатталады?
2.Қиылысатын түзулер жазықтықты неше бұрышқа
бөледі?
3. Қандай бұрыштар вертикаль бұрыштар деп
аталады?
VII. Жаңа сабақты
бекіту
№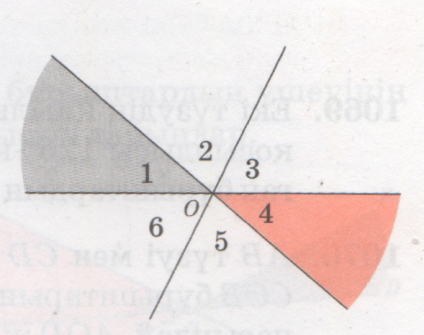 1064
1064
<1=<4;
<2=<5;
<3=<6.
№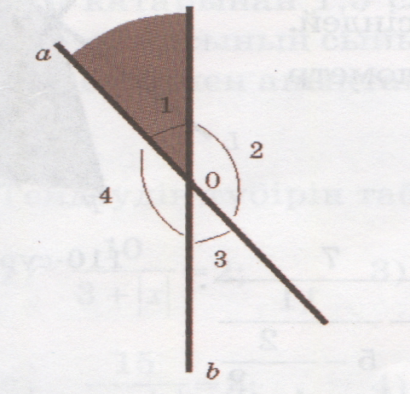 1066
1066

<1+<2= , осыдан <2=
, осыдан <2=
<2+<3=  ,осыдан<3=
,осыдан<3=
<3+<4= осыдан<4=
осыдан<4=
№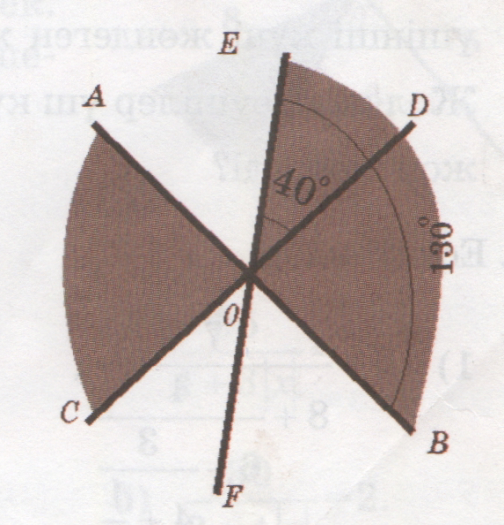 1067
1067
<EOD=400
<EOB=1300
<EOB=<EOD+<DOB
<DOB=<EOB-<EOD=1300-400=900
<AOC=<DOB
<AOC=900
№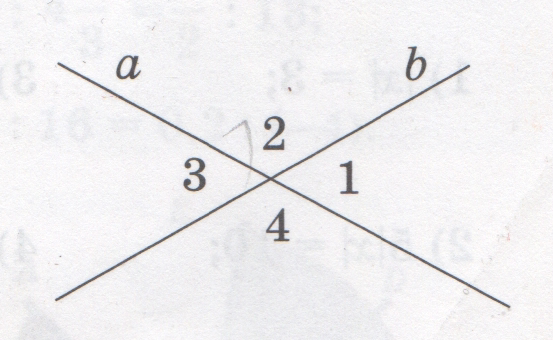 1069
1069
<1+<3=1260
<1=<3=1260/2=630
<2=<4=1800-630=1170

№1070
<AOC:<COB=5:7
<AOC=<BOD,
<COB=<AOD
<AOC+<COB=1800
<AOC=5x,
<COB=7x
5x+7x=1800
12x=1800
x=1800:12=150
<BOD=<AOC=5*150=750 <AOD=<COB=7*150=1050
№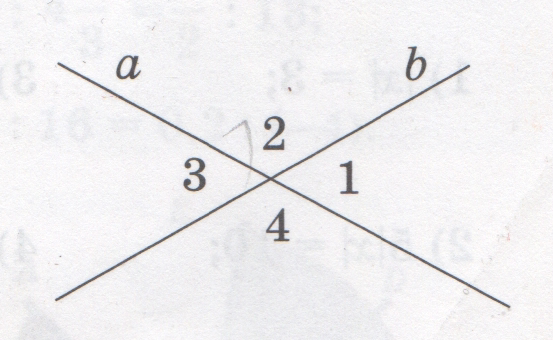 1071
1071
1)
<1=750
<1=<3=750
<2=<4=1800-750=1050
2)
<1=1200
<1=<3=1200
<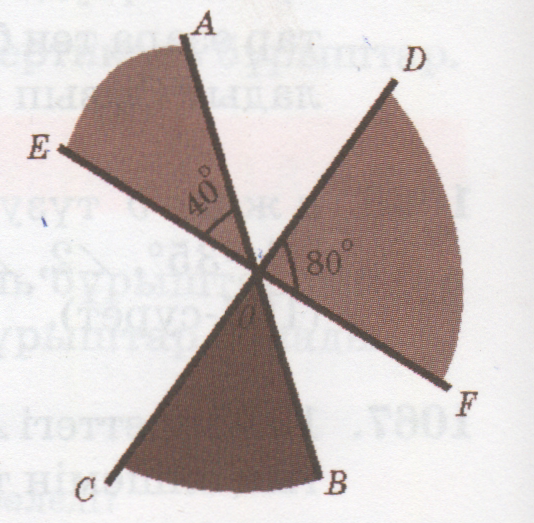 2=<4=1800-1200=600
2=<4=1800-1200=600
№1072






№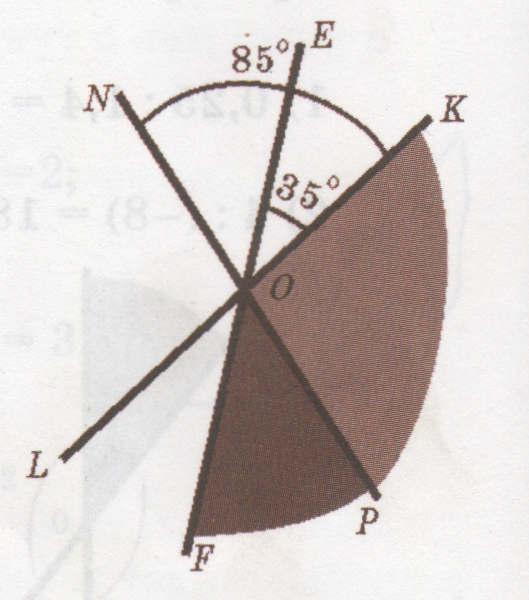 1073
1073





№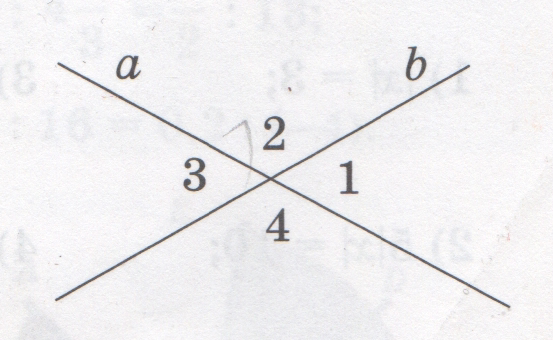 1076
1076




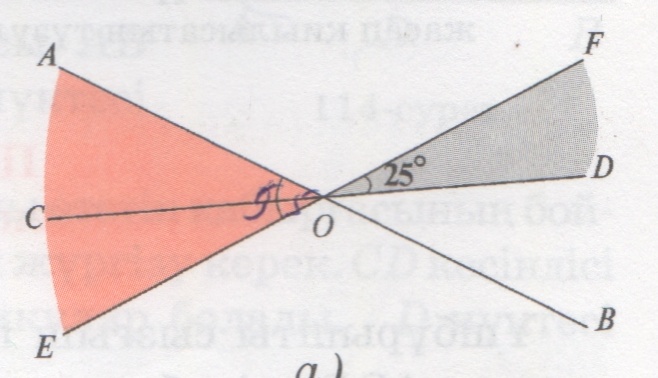
№1077
<AOE=550
<DOF=250
<AOB=1800
<AOB=<AOE+<BOE
<BOE=<AOB-<AOE=1800-550=1250
<BOF=<AOE=550 <BOF=<DOF+<BOD
<BOD=<BOF-<DOF=550-250=300
№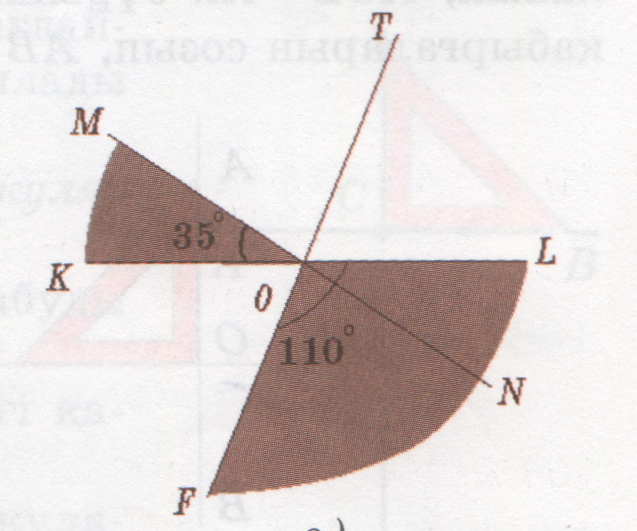 1078
1078
<FOL=1100
<KOM=350
<KOL=1800
<KOL=<FOL+<KOF
<KOF=<KOL-<FOL=1800-1100=700
<KOT=<FOL=1100
<KOT=<KOM+<MOT
<MON=<KOT-<KOM=1100-350=750
№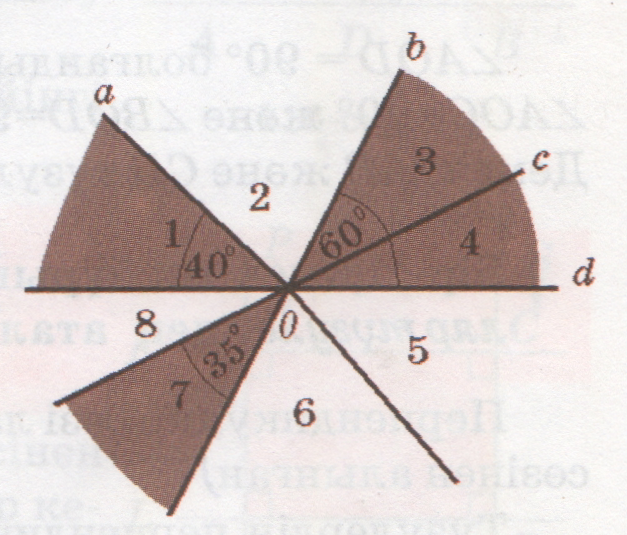 1079
1079
<1=400;
<3+<4=600
<7=350
<1=<5;
<2=<6;
<3=<7
<4=<8;
<1+<2+<3+<4=1800
<2=1800-400-600=800 <6=800.
<3=<7=350 <3+<4=600 <4=600-350=250 <8=250
IV. Үйге
тапсырма:№1081
Қорытынды:оқушылардың есептер шығаруына қарай
бағалау.










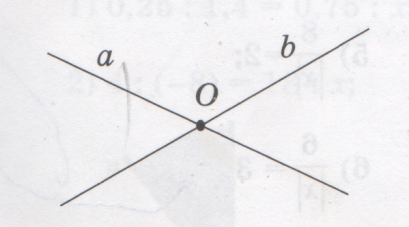
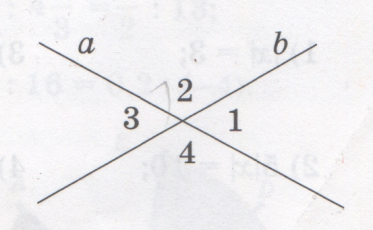

 және <2 бір жазыңқы бұрышты
құрайды.
және <2 бір жазыңқы бұрышты
құрайды.


 осыдан
осыдан
 және
және  тың, сол сияқты <2 және <4 –
тың біреуінің қабырғалары екіншісінің қабырғаларымен толықтауыш
сәулелер.
тың, сол сияқты <2 және <4 –
тың біреуінің қабырғалары екіншісінің қабырғаларымен толықтауыш
сәулелер. 1064
1064 1066
1066



 1067
1067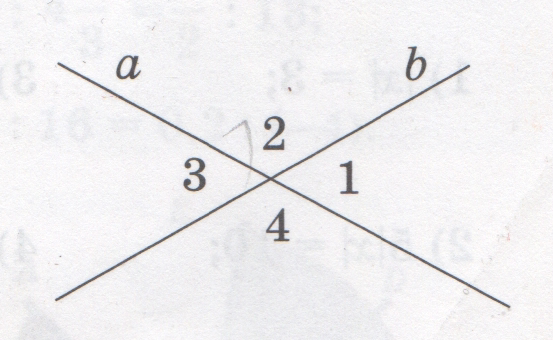 106
106
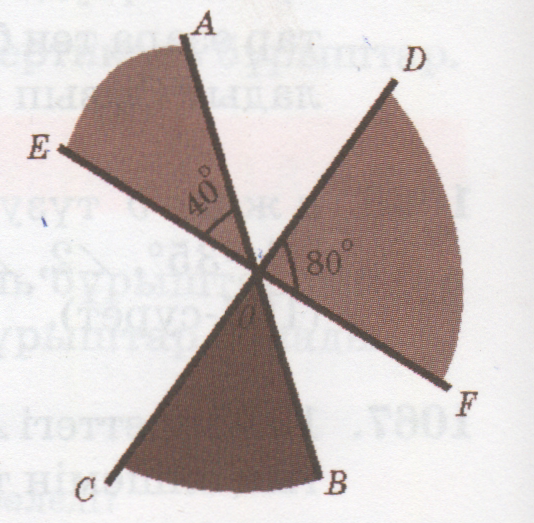 2=<4=180
2=<4=180