МАЗМҰНЫ

КІРІСПЕ............................................................................................................................3

І. ҚОСКИНЕМАТИКА БӨЛІМІ

1.1. Қатты денелердің айналмалы қозғалысы................................................................4

1.2. Механикалық бірліктер...................................................................................................13

ІІ. МОЛЕКУЛА-КИНЕТИКАЛЫҚ ТЕОРИЯ ЖӘНЕ ТЕРМОДИНАМИКА

2.1. Молекула-кинетикалық теорияның және термодинамиканың физикалық негіздері............................................................................................................................15

2.2 Электромагниттік тербелістер және толқындар...................................................28

ҚОРЫТЫНДЫ....................................................................................................................30

ПАЙДАЛАНЫЛҒАН ӘДНБИЕТТЕР ТІЗІМІ.........................................................................31

КІРІСПЕ

Қос кинематика жылжымалы бөлімдер өзара байланысын немесе бір бөлімнің басқаға ауысу мүмкіндігін жылжымайтын бөліммен біріктіреді. Өзара байланысқан жəне олардың өзара қозғалысына жол беретін екі бөлім қос кинематиканы түзеді. Бөлімдердің қос кинематикаға қосылу мүмкіндіктері əртүрлі болады. Айналмалы қос кинематиканы қарастырайық (1.2. сур), мұнда білік 1 – мойын тірек – 2 бөлімдер ұдайы жанасатын екі цилиндр арқылы байланысады. Білік буылтықтары бір цилиндрдің екіншісіне қарай х-х осьі бағытында ауысуына кедергі келтіреді, осы ретте олардың бірінің екіншісіне қатысты айналуына кедергі келтірмейді.

Қандай болмасын, айналу осімен салыстырғандағы F күштің М моменті төмендегі формуламен анықталады:

мұндағы l-айналу осінен бойымен күш әсер ететін түзуге дейінгі қашықтық.

Материялық нүктенің қандай болмасын айналу осіне қатысты инерция моменті деп мына шаманы айтамыз: ,

мұндағы т — материялық нүктенің массасы, ал — нүктенің осьтен қашықтығы.

Қатты дененің оның айналу осі арқылы алынған инер­ция моменті

мұнда интегралдауды дененің барлық көлемі арқылы жүргізу керек. Интегралдау жүргізе отырып мынадай формулалар алуға болады:

1) өзінің осі арқылы алынған тұтас біртекті цилиндрдің инерция моменті

мұндағы R — цилиндрдің радиусы, ал m — оның массасы.

2) цилиндр осінс қатысты ішкі радиусы R₁және сыртқы радиусы ₂ қуыс цилиндрдің (құрсаудың) инерция моменті ,

жұқа қабырғалы қуыс цилиндрдің R₁ R₂ = R және

3) шардың центрінен өтетін оське қатысты радиусы біртекті шардың инерция моменті.

Бұл шектеулер кинематикалық жұпта шартты байланыстар деп аталады. Жалпы жағдайда кеңістікте əртүрлі еркін қозғалатын дене еркіндіктің алты деңгейіне ие, яғни кеңістікте үш ось бойында ілгерілемелі орын ауыстыра алады (x, y, z) (1.4-сурет), сонымен қатар осы осьтерге қатысты айналады. Нəтижесінде, қос кинематика бөлімдерінің салыстырмалы қозғалыстары байланыс шарттарымен шектелген. Осы байланыстардың саны əртүрлі болуы мүмкін, бірақ бесеуден артық емес. Олай болмаған жағдайда бөлімдер салыстырмалы қозғалысты жоғалтады, ал қос кинематика екі бөлімнің қатты қосындысына ауысады. Басқаша айтқанда, байланыстар шартының саны бірліктен төмен бола алмайды, себебі бұл жағдайда байланыстар саны нөлге тең, бөлімдер жанаспайды, ал қос кинематика тіршілігін жояды.

І. ҚОСКИНЕМАТИКА БӨЛІМ

1.1. Қатты денелердің айналмалы қозғалысы

Қос кинематика Жылжымалы бөлімдер өзара байланысын немесе бір бөлімнің басқаға ауысу мүмкіндігін жылжымайтын бөліммен біріктіреді. Өзара байланысқан жəне олардың өзара қозғалысына жол беретін екі бөлім қос кинематиканы түзеді. Бөлімдердің қос кинематикаға қосылу мүмкіндіктері əртүрлі болады. Айналмалы қос кинематиканы қарастырайық (1.2. сур), мұнда білік 1 – мойын тірек – 2 бөлімдер ұдайы жанасатын екі цилиндр арқылы байланысады. Білік буылтықтары бір цилиндрдің екіншісіне қарай х-х осьі бағытында ауысуына кедергі келтіреді, осы ретте олардың бірінің екіншісіне қатысты айналуына кедергі келтірмейді.

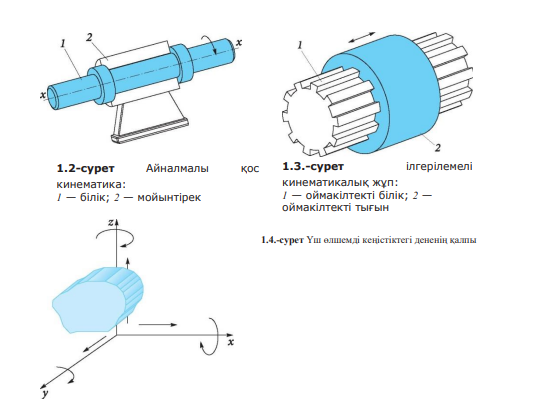
1.3-суретте бөлімдер байланысының басқа сызбасы көрсетілген. Оймакілтекті білік 1 осьтік бағытта ауыса алады осы ретте оның оймакілтекті төлкеге 2 қатысты айналуы мүмкін емес Осылайша, кез келген бөлімнің қозғалысына қос бөлімді біріктіретін тəсілге тəуелді белгілі бір шектеулер қойылады. Бұл шектеулер кинематикалық жұпта шартты байланыстар деп аталады. Жалпы жағдайда кеңістікте əртүрлі еркін қозғалатын дене еркіндіктің алты деңгейіне ие, яғни кеңістікте үш ось бойында ілгерілемелі орын ауыстыра алады (x, y, z) (1.4-сурет), сонымен қатар осы осьтерге қатысты айналады. Нəтижесінде, қос кинематика бөлімдерінің салыстырмалы қозғалыстары байланыс шарттарымен шектелген. Осы байланыстардың саны əртүрлі болуы мүмкін, бірақ бесеуден артық емес. Олай болмаған жағдайда бөлімдер салыстырмалы қозғалысты жоғалтады, ал қос кинематика екі бөлімнің қатты қосындысына ауысады. Басқаша айтқанда, байланыстар шартының саны бірліктен төмен бола алмайды, себебі бұл жағдайда байланыстар саны нөлге тең, бөлімдер жанаспайды, ал қос кинематика тіршілігін жояды. Осылайша, байланыс шарттарының саны

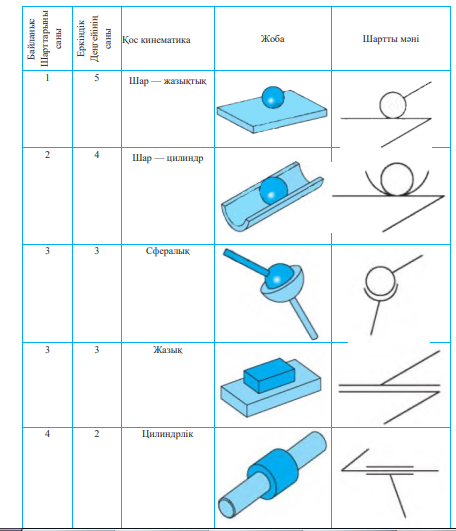
S = 1— 5. Яғни, қос кинематика H бөлімінің еркіндік деңгейінің саны H = 6 – S байланыста көрсетілуі мүмкін. Еркіндік деңгейлерінің саны бойынша қос кинематиканың жіктеулері жəне олардың шартты мəндері

1.1 - сурет. Қос кинематиканың жіктелуі

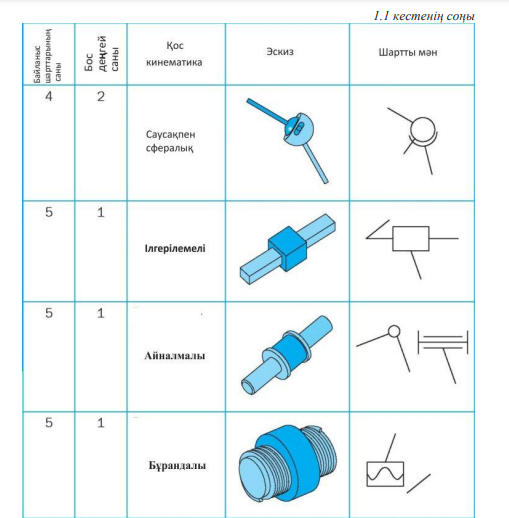
Қалған қозғалыстар бір-біріне тәуелсіз немесе байланысты болуы мүмкін, яғни оларға қосымша геометриялық шарттар салынады. Мысалы, қос кинематикада бұрама – бұранда (1.5. сурет) бұранданың 1 өз осі бойында айналуы оның бұрама 2 айналасында ілгерілемелі қозғалысын туындатады. Кинематикалық жұп элементтерінің ұдайы бір-бірімен жанасуы үшін олар тұйық болуы керек. Тұйықталу не геометриялық не күштік тəсілмен жүзеге асырылады. Геометриялық тұйықталу геометриялық будың тиісті геометриялық элементтері арқылы жүзеге асырылады. Мысалы

Жалпы жағдайда түзу сызықты қозғалыстың жылдамдығы

Үдеуі

Түзу сызықты бір қалыпты қозғалыс болғaн жағдайда υ= constжәне = 0.

Түзусызықтыбірқалыптыайнымалықозғалыскезінде

, , = const.

Бұлтеңдеулердеүдеу бірқалыптыүдемеліқозғалыскезіндеоңболадыда, албірқалыптыбаяуқозғалыскезіндетерісболады.

Қисықсызықтықозғалыскезіндетолықүдеу ,

мұндағы _t— тангенциалүдеу, ал — нормаль (центргетартқышүдеу) үдеу, сондықтан

_{t ,}

мұндағыυ -қозғалыстыңжылдамдығы, алR — берілгеннүктедегітраекторияныңқисықтықрадиусы.

Айналмалықозғалыстажалпыжағдайындабұрыштықжылдамдық

Ал бұрыштықүдеу

Бip қалыптыайналмалықозғалыскезіндебұрыштықжылдамдық

,

Мұндағы

Т - айналупериоды,

ν — айналу жиілігі, яғни (бірлік уақыт ішіндегі айналым саны Бұрыштық жылдамдықтың сызықтық жылдамдықпен өзара байланысымына қатынаспен анықталады:

Тангенциалжәненормальүдеулерайналмалықозғалыстамынадайтүрдекөрсетілуімүмкін: ,

(6 - кестедеілгерілемеліқозғалыстеңдеуініңайналмалықозғалыстеңдеуіменсалыстырмасыберілген.

1 – кесте

Динамиканың негізгі заңы (Ньютонның екінші заңы) мына теңдеумен өрнектеледі:

Fdt = d(mυ).

Егер масса тұрақты болса, онда ,

Мұндағы а — F күштің әсерінен массасы m дененің алатын үдеуі.

F күштің s орын ауыстырғандағы жұмысы мынадай формуламен өрнектелуі мүмкін:

мұндағы F_s— жол бағытындағы күштің проекциясы, ds — жол учаскесінің шамасы. Иптегралдау s жолына тұтас таралуға тиіс. Кей жағдайда орын ауыстыруға тұрақты бұрыш жасай әсер ететін тұрақты күшке мынаны аламыз: ,

мұндағы — F күш пен s жүрген жол арасындағы бұрыш.

Қуат төмендегі формуламен анықталады: .

Тұрақты қуат жағдайында ,

мұндағы А — t уақыт ішіндегі істеліпетін жұмыс.

Сондай-ақ қуатты мынадай формуламен анықтауға болады: N = Fυcos a,

яғни қуат қозғалыс жылдамдығының қозғалыс бағытындағы күш проекциясының көбейтіндісімен анықталады.

v жылдамдықпен қозғалатын, массасы т дененің кинетикалық энергиясы мынаған тең: .

Әсер етуші күштің сипатына қарай, потенциалық энсргияның формуласы әр түрлі болады.

Изоляцияланған системада оған енетін барлық денелердің қозғалыс мөлшері тұрақты болып қалады, яғни

.

Массалары т₁ және m₂екі денепің серпімсіз центрлік соғылысқан кезде осы денелердің соғылысқаннан кейінгіқозғалысының жалпы жылдамдығын төмендегі формуламен табуға болады: .

мұндағы — соғылғанға дейінгі бірінші дененің жылдамдығы, ал — соғылғанға дейінгі екінші дененің жылдамдығы.

Денелер серпімді центрлік соғылысқан кезде әр түрлі жылдамдықпен қозғалатын болады. Соғылысқаннан кейінгі бірінші дененің жылдамдығы ,

соғылысқаннан кейінгі екінші дененің жылдамдығы .

Қисық сызықты қозғалыста материялық нүктеге әсер ететін күшті екі құраушы күшке жіктеуге болады: тангенциаль және нормаль күштерге.

Нормаль құраушы

центрге тартқыш күш болады. Мұнда υ— массасы т дененің қозғалысының сызықтық жылдамдығы, R — берілген пүктедегі траекторияның қисықтық радиусы.

Серпімді деформация х туғызатын күш деформацияның шамасына пропорционал, яғни F = kx,

мұндағы k — бірге тең деформация туғызатын, сан жағынан күшке тең коэффицент (деформация коэффициенті).

Серпімді күштің потенциал энергиясы

Екі материялық нүкте (яғни өлшемдері олардың өз ара қашықтықтарына қарағанда кішкене больп келетін денелер) бір-біріне мынадай күшпен тартылады: ,

мұндағы тартылыс тұрақтысы немесе гравитациялық тұрақты, бұл тең = 6,67 • 10^-11м³/кг • сек²,т₁ және т₂ — өз араәсер ететін материялық нүктелердің массасы; R— олардың ара қашықтығы. Бұл заңды біртекті шарларға да қолдануға болады. Сонда R — олардың центрлерінің ара қашықтығы болады.

Тартылыс күшінің потенциалық энергиясы

«Минус» таңбасы R— болғандағы өз ара әсер етуші екі денелердің потенциалық эпергиясының нолге тең болатындығын көрсетеді, ал бұл денелер бір-біріне жақындағанда потенциал энергия кемиді.

Кеплердің үшінші заңы мына түрде болады:

мұндағы Т₁және Т₂— планеталардың айналып шығу пе­риоды, R₁жәпе R₂— олардың орбиталарының үлкен жар­ты остері. Дөңгелек орбита жағдайында үлкен жарты осьтің ролін орбита радиусы атқарады.

Қандай болмасын, айналу осімен салыстырғандағы F күштің М моменті төмендегі формуламен анықталады:

мұндағы l-айналу осінен бойымен күш әсер ететін түзуге дейінгі қашықтық.

Материялық нүктенің қандай болмасын айналу осіне қатысты инерция моменті деп мына шаманы айтамыз: ,

мұндағы т — материялық нүктенің массасы, ал — нүктенің осьтен қашықтығы.

Қатты дененің оның айналу осі арқылы алынған инер­ция моменті

мұнда интегралдауды дененің барлық көлемі арқылы жүргізу керек. Интегралдау жүргізе отырып мынадай формулалар алуға болады:

1) өзінің осі арқылы алынған тұтас біртекті цилиндрдің инерция моменті

мұндағы R — цилиндрдің радиусы, ал m — оның массасы.

2) цилиндр осінс қатысты ішкі радиусы R₁және сыртқы радиусы ₂ қуыс цилиндрдің (құрсаудың) инерция моменті ,

жұқа қабырғалы қуыс цилиндрдің R₁ R₂ = R және

3) шардың центрінен өтетін оське қатысты радиусы біртекті шардың инерция моменті

4) стерженьнің ортасынан өткен оське қатысты біртекті стерженьнің инерция моменті оның ұзындығына пер­пендикуляр .

Егер қандай болмасын дененің ауырлык центрінен өтетін оське қатысты инерция момснті ₀ белгілі болса, онда бірішні оське параллель болатын кез келген ось арқылы алынған инерция моментін Штейнер формуласымен табуға болады: ,

мұндағы т — дененің массасы, ал d — ауырлықцентрінен айналу осіне дейінгі қашықтық.

Айналмалы қозғалыс динамикасының негізгі заңы төмендегі теңдеумеи көрсетіледі:

,

мұндағы М — инерция моменті -ге тең денеге түсірілген күш моменті; — дененің айналысының бұрыштық жылдамдығы. Егер = const болса, онда

мұндағы — айналыс моментінің М әсерінен дененің алатын бұрыштық үдеуі.

Айналатын дененің кинетикалық энергиясы

мұндағы — дененіц инерция моменті, ал — оның бұрыштық жылдамдығы.

Айналмалы қозғалыс динамикасы теңдеуінің ілгерілемелі қозғалыстыц теңдеуімен салыстырмасы 7-кестеде берілген.

Физикалық маятниктің кіші тербелістерінің периоды

мұндағы — маятниктің осіне қатысты инерция моменті, m — маятниктің массасы, d — айналу осінен ауырлық центрге дейінгі қашықтық, g— ауырлық күшінің үдеуі.

2-кесте

Сығылмайтынидеал сұйықтың қалыптасқан қозғалысы үшін Бернулли теңдеуі алынады.

.

Мұндағы — сұйықтың тығыздығы, υ— трубаның берілген қимасындағы сұйық қозғалысының жылдамдығы, — трубаның берілген қимасының кейбір деңгейден алынған биіктігі және р — қысым. Бериуллидің теңдеуінен, кішкентай тесіктен сұйықтың ағып шығу жылдамдығы υ=

мұндағы — тесіктен жоғары қарай алынған сұйықтың бетіне дейінгі биіктік. Қандайда бол-масын трубаның көлденең қимасынан бірдей көлемдегі сұйық өтетін болғандықтан, болады, мұндағыυ₁ және υ₂— көлденең қималарының ауданы, S₁және S₂ трубаның екі қимасынан өтетін сұйықтардың жылдамдығы.

Тұтқыр сұйықта (немесе газда) құлайтын шарикке жасалатын кедергі күш Стокс формуласымен анықталады: ,

мұндағы — сұйықтың немесе газдың ішкі кедергісінін коэффициенті (динамикалық тұтқырлық), — шариктің радиусы, υ— оның жылдамдығы. Стокстың заңы тек қана ламинарлық қозғалыс үшін берілген. Ламинарлық қозғалыс кезінде t уақыт ішімде радиусы және ұзындығы капиляр түтік арқылы ағып өтетін сұйықтың (газдың) көлемі Пуазейль формуласымен анықталады

мұндағы — сұйықтың (газдың) динамикалық тұтқырлығы, р — түтік ұштарындағы қысымдардың айырымы.

Сұйық (газ) қозғалысының сипаты Рейнольдстің өлшемсіз саны арқылы анықталады

,

мұндағы D — сұйықтықпен (газбен) ағатын дененің сызықтық мөлшерін сипаттайтын шама, υ— сұйықтың ағу жылдамдығы, — тығыздық, — динамикалық тұтқырлық. Қатынас v = /p кинематикалық тұтқырлық деп аталады.

Ламинарлық қозғалыстан турбулентті қозғалысқа ауысуды анықтайтын Рейнольдс санының кризистік мәні әр түрлі формалы денелерде түрліше болады.

Есептер шығару кезінде қажет нұсқаулар

Еселік және үлестік бірліктерін жасауға арналған косымшалар

3 - кесте

2. Механикалық бірліктер

4-кесте

5 –кесте

ІІ. МОЛЕКУЛА-КИНЕТИКАЛЫҚ ТЕОРИЯ ЖӘНЕ ТЕРМОДИНАМИКА

2.1. Молекула-кинетикалық теорияның және термодинамиканың физикалық негіздері

Идеал газдар Менделеев — Клапейрон күйінің теңдеуіне бағынады:

мұндағы -газдың кысымы, V- оның көлемі, Т - абсолют температура, М — газдың массасы, — бір киломоль газдың массасы, R— газ тұрақтысы; қатынасыкиломольдің санын береді.

ХЖ бірлігінде газ тұрақтысының сан мәні R = 8,31 • 10³дж/кмоль • град-қа тең болады.

Далтонның заңы бойынша газдар қоспасының қысымы оның парциал қысымының қосындысына тең болады, осы берілген температурада барлық көлемді жеке өзі толтыратындай әрбір жеке газдарда болатын қысым.

Газдардың кинетикалық теориясының негізгі теңдеуінің түрі төмендегідей: ,

мұндағы п — бірлік көлемдегі молекуланың саны, W₀— бір молекуланың ілгерілемелі қозғалысының кинетикалық энергиясы, т — молекуланың массасы және — молекуланың орташа квадраттық жылдамдығы.

Бұл шамалар мынадай формулалармен анықталынады.

Бірлік көлемдегі молекуланың саны ,

мұндағы - тұрақтысы, N₀— Авогадросаны. R= 8,31 • І0³дж/кмоль• граджәне ₀ = 6,02• 10²⁶кмоль^-1 болғандықтан, k = 1 ,38 • 10^-23дж/град= 1,38 • 10^-16эрг/град болады.

Молекуланың ілгерілемелі қозғалысының орташа кинетикалық энергиясы

Молекуланың орташа квадраттық жылдамдығы

сонымен бірге

Молекулалардың жылулық қозғалысының энергиясы (газдың ішкі энергиясы) ,

мұндағы і — молекуланың еркіндік дәрежесінің саны.

Молекулалық жылу сыйымдылығы С-пен меншікті жылу сыйымдылығы с-нің арасындағы байланыс олардың анықтамасынан шығады

Көлем тұрақты болғанда газдың молекулалық жылу сыйымдылығы

қысым тұрақты болғанда

Осыдан молекулалық жылу сыйымдылығы түгелдей газмолекуласының еркіндік дәрежесінің санымен анықталады. Бір атомды газ үшін і=3, және

C_v = 12,5 • 10³дж/кмоль • град =З кал/моль • град,

С_р = 20,8 • 10³дж/кмоль • град = 5 кал/моль • град.

Екі атомды газ үшін i = 5 және

C_v=20,8 • 10³дж/кмоль • град =5 кал/моль • град,

Cp=29,l • 10³дж/кмоль • град= 7 кал/моль • град.

Көп атомды газ үшін i = 6 және

С_v=24,9 • 10³дж/кмоль • град = 6 кал/моль • град.

С_р = 33,2 ·10³дж/кмоль • град=8 кал/моль • град.

Молекулалардың жылдамдықтарына қарай бөліну заңы (Максвелл заңы), салыстырмалы жылдамдықтары и мен и интервалында жатқан молекулалардыңсанып табуға мүмкіндік береді:

мұндағы салыстырмалы жылдамдық,υ — берілген жылдамдық және

молекулалардыңанағұрлым ықтимал болатын жылдамдығы,

6- кесте

— жылдамдық u-ға қарағанда салыстырмалы жылдамдық интервалының кіші шамасы.

Молекулалардың жылдамдықтарына қарай бөліну заңына есеп шығарғанда әр түрлі -ға -мәндері берілген 10-таблицаны пайдаланған ыңғайлы.

Молекулалардың орташа арифметикалық жылдамдығы

.

Көптеген жағдайларда и жылдамдықтың берілген мәнінен жылдамдыктары асып түсетін N_xмолекулалардыңсанын білу өте қажет болады. 11- кестеде , мұндағы N — молекулалардың жалпысаны.

11-кесте

Барометрлік формула, ауырлық күшінің өрісіндегі газ қысымының кемуінің заңын береді

мұндағы , — биіктіктегі газдың қысымы, р₀— =0 биіктіктегі қысым, g— ауырлық күшінің үдеуі. Бүл фор­мула жуықталынған формула, себебі биіктіктердің айырымының үлкен мәніне Т температураны бірдей деп есептеуге болмайды.

Газ молекуласының еркін жолының орташа ұзындығы

,

мұндағы — арифметикалық орташа жылдамдық, — әрбір молекуланың бірлік уақыт ішіндегі басқа молекулалармен соғылуының орташа саны, — молекуланың эффектілік диаметрі және п — бірлік көлемдегі молекулалардың саны. Бірлік көлемдегі барлық молекула-лардың бірлік уақыт ішіндегі соғылу саны

,

Диффузия кезінде уақыт ішінде көшірілген М мас­са төмендегі теңдеумен анықталады:

,

мұндағы - ауданға перпендикуляр бағыттағы тығыздық градиенті, ал - диффузия коэффиценті. Ол мынаған тең:

мұндағы — орташа жылдамдық, — молекуланың еркін журісінің орташа ұзындығы.

уақыт ішінде газ арқылы көшірілген қозғалыс мөлшері газдағы F ішкі үйкеліс күшін анықтайды ,мұндағы - ауданға перпендикуляр бағыттағы газ ағынының жылдамдық градиенті, ал - ішкі үйкеліс коэффиценті (динамикалық тұтқырлық) .

уақыт ішінде жылу өткізгіштік нәтмжесіндекөшірілген жылу мөлшері мынаған тең:

,

мұндағы - ауданға перпендикуляр бағыттағы температураның градиенті, К- жылу өткізгіштік коэффиценті

Термодинамиканың бірінші бастамасын төмендегі түрде жазуга болады,

мұндағы dQ — газдың алған жылу мөлшері; dW — газдың ішкі энергиясының өзгерісі және dA = pdV – көлемін өзгерткен ксздс газдың істейтін жұмысы. Газдың ішкі энергиясының өзгерісі

,

мұндағы dT — температураның өзгерісі. Газдың, көлемі өзгермегендегі, толық жұмысы

.

Газ көлемінің изотермалық өзгерісі кезіндегі істелінетін жұмыс .

Адиабаталық процесс кезінде газдың қысымы мен оның көлемі арасындагы байланыс Пуассонтеңдеуі арқылы көрсетіледі р = const,

яғни ,мұндағы .

Пуассонның теңдеуін мынандай түрде де жазуға бо лады: ,

яғни , немесе ,яғни .

Газдың көлемі адиабаталы өзгергенде істелетін жұмысты төмендегі формуламен табуға болады:

Политропиялық процесс теңдеуінің түрі төмендегідей болады: ^,

Немесе

мұндағы п — политропа көрссткіші (1< <х).

Жылу машинасыпың пайдалы эсер коэффициенті

,

мұндағы Q₁ — жұмысшы денеге берілген жылу, алQ₂—'суытқышқа берілген жылу. Карноның идеал циклі үшін

мұндағы Т₁— қыздырғыштың температурасы, Т₂— суытқыштың температурасы.

В мен А екі күйдің энтропияларының айырымы s_в— s_атөмендегі формуламен анықталады: .

Нақты газдар Бір киломоль үшін берілгеп нақты газ күйінің теңдеуі (Ван-дер-Ваальс теңдеуі) төмендегідей: