Арифметикалық прогрессияның алғашқы n - мүшесінің формуласы

1 слайд
Арифметикалық прогрессияның алғашқы n – мүшесінің қосындысының формуласы»

1 слайд

2 слайд
Алгебра 9 сынып «Математика тіпті хаос кезіндеде белгілі бірізділікті сақтап қалады». арифметической прогрессиейчпрвае(Гертруда Стайн)

2 слайд

3 слайд
ҚАЙТАЛАЙМЫЗ БА? Арифметикалық прогрессияның анықтамасын айтайық; Тізбектің екінші мүшесінен бастап, әрбір мүшесі өзінің алдындағы көршілес мүшесіне бірдей тұрақты санды қосқанға тең болса, онда бұл тізбек арифметикалық прогрессия деп аталады , ал d (айырмасы) деп аталады.

3 слайд

4 слайд
Мынадай арифметикалық прогрессия берілген: 2, 6, 10, 14,….. а1= 2 d = 6-2 = 4 а11 = 2+ 10 4 = 42 dпаа n 1 1 n – ші мүшенің формуласын табайық:

4 слайд

5 слайд
Үй жұмысын тексеру: № 217

5 слайд

6 слайд

6 слайд

7 слайд
22.11.2017 Сабақтың тақырыбы: «Арифметикалық прогрессияның алғашқы n мүшесінің қосындысы»

7 слайд

8 слайд
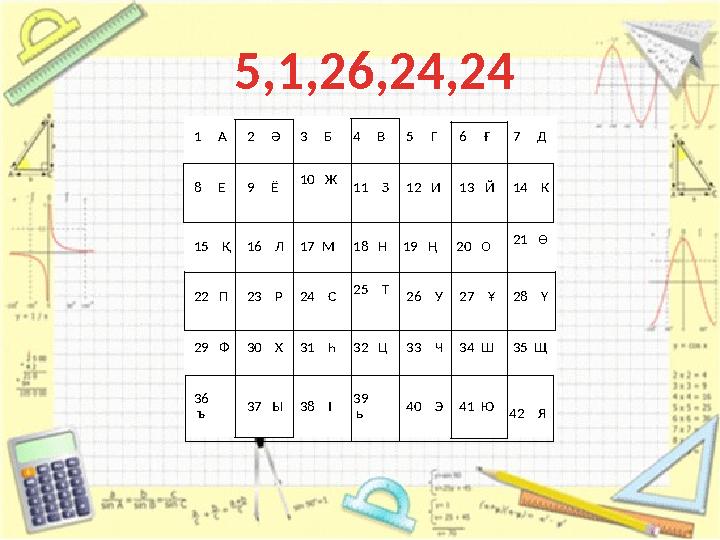
 1     А  2     Ә  3     Б  4     В  5     Г  6     Ғ  7     Д  8     Е  9     Ё  10    Ж  11     З  12    И  13    Й  14     К  15     Қ  16     Л  17   М  18    Н   19    Ң     20    О    21    Ө  22    П  23     Р  24     С  25     Т  26     У  27     Ұ  28     Ү  29    Ф  30     Х  31     Һ  32    Ц  33     Ч  34   Ш  35   Щ  36        ъ   37    Ы  38     І  39        ь  40     Э  41   Ю   42     Я  5,1,26,24,24

8 слайд

9 слайд
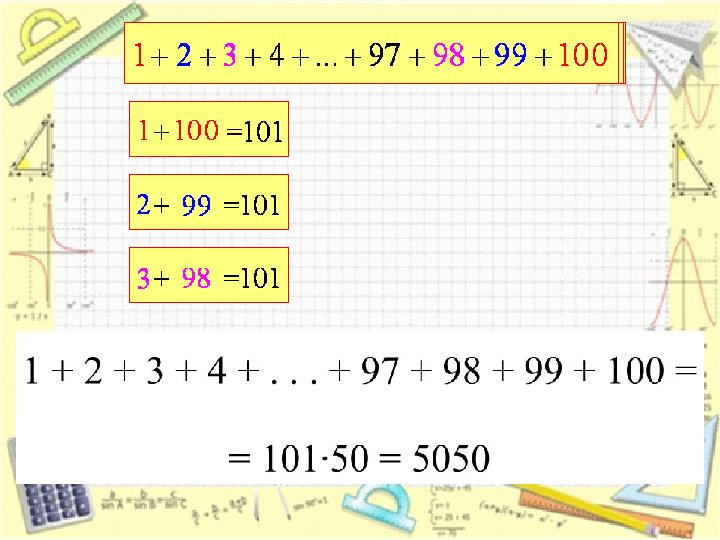
Математика тарихынан: Алғашқы n- мүшенің қосындысын табу формуласымен байланысты ұлы неміс математигі Карл Фридрих Гаусстың(1777- 1855) өмірінің бір үзінді сәті бар. Гаусс 9 жастында бастауыш мұғалімі даптер тексеріп отырған күйі оқушыларға мынадай күрделі тапсырма берсем, көп ойланады ғой деп: « 1 ден 100 ге дейінгі барлық натурал сандардың қосындысын табуды тапсырыпты», екі минуттан кейін оқушылардың бірі «мен шештім…» деген кезде мұғалімнің таң қалқалысында шек болмапты.

9 слайд

10 слайд
Топпен жұмыс Ертеректе бір данышпан айтқан екен, сан тізбегінің басы мен соңын қосу керек деп.

10 слайд

11 слайд

11 слайд

12 слайд
Сонда қандай формуланы іздейміз? n aa S n n 2 1  

12 слайд

13 слайд
Формуланы қорыту: Берілгені: ÷ а1, а2, а3, а4, ……., аn Дәлелдеу:а1 + аn = a2+ an-1 a2 = a1 + d, осыдан a1 = a2 – d, яғни an-1 = an – d және де a3+ an-2 = а1 + аn ….. ak+ an-k+1 = а1 + аn Осылайша:

13 слайд

14 слайд
Арифметикалық прогрессияның алғашқы n мүшесінің қосындысын деп белгілейміз: n S nnn aaaaS  121 ... Немесе 121...aaaaS ппn   Осы екі теңдіктің әрбір мүшесін қосып, мынаны аламыз:      ....2 121121 ааaaааaaS пnппn        ....2 1111 п п пппn аапaaааaaS   Осыдан формула шығады:   2 1 пaa S п n   nnn aaaaS  121 ... ЧТД

14 слайд

15 слайд
Арифметикалық прогрессияның алғашқы n мүшесінің қосындысы, тізбектің екі шеткі мүшелерінің жарты қосындысын олардың санына көбейткенге тең . Жалпы мүшесі болғандықтан:  n пda S n    2 12 1   2 1 пaa S п n   dпаа n 1 1

15 слайд

16 слайд
Мысал: Берілген арифметикалық прогрессияның алғашқы 20 мүшесінің қосындысын табыңдар : 1; 3; 5; 7;… .   2 1 пaa S п n   а1 = 1 d = 2 a20 = 1+ 19 2 =39 ∙ S20 = (1+39)10 = 400 Жауабы: 400

16 слайд

17 слайд
Оқулықпен жұмыс № 251 , 252, 253 есептерді шығару

17 слайд

18 слайд
Топпен жұмыс 1 ТОП 2 ТОП •Берілгені: а1 = 5, • а10 = 23 Табу керек: S10 • Берілгені: а1 = -2, d = 1 Табу керек : S50 •Берілгені: а1 = 4, • а12 = 16 Табу керек: S12 •Берілгені: а1 = -1, d = 2 Табу керек: S40 3 ТОП 4 ТОП

18 слайд

19 слайд
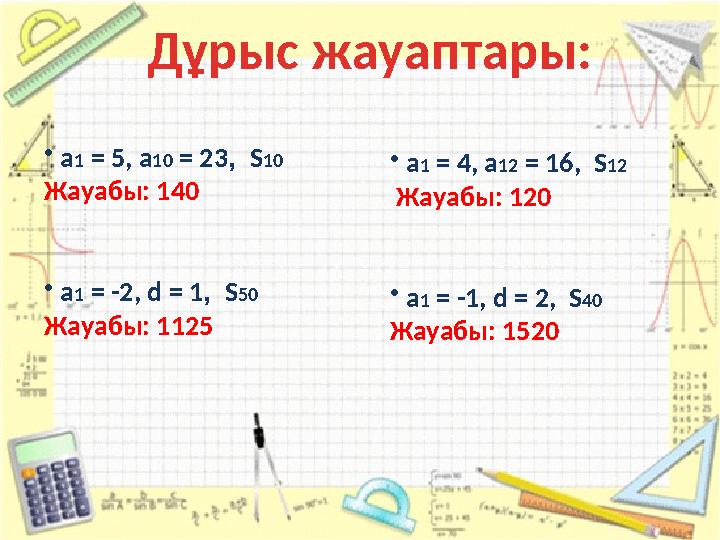
Дұрыс жауаптары: • а1 = 5, а10 = 23, S10 Жауабы: 140 • а1 = -2, d = 1, S50 Жауабы: 1125 • а1 = 4, а12 = 16, S12 Жауабы: 120 • а1 = -1, d = 2, S40 Жауабы: 1520

19 слайд

20 слайд
Біздің өміріміздегі прогрессияның мысалдарын іздестірейік:

20 слайд

21 слайд
Үйге тапсырма: № 253

21 слайд

22 слайд
Сабақ туралы пікірлеріңізді «Білім ағашына» қалдырыңыздар!

22 слайд