Материалдар / Бір айнымалысы бар сызықтық теңсіздік 5 сынып

Бір айнымалысы бар сызықтық теңсіздік 5 сынып

Материал туралы қысқаша түсінік

мұғалімдерге

Амангельдиева Динара Сержанқызы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

31 Шілде 2019

623

0 рет жүктелген

Математика Презентация 5 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 24

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
АҚПАННЫҢ 23-І «Достық тілек»

1 слайд

АҚПАННЫҢ 23-І «Достық тілек»

2 слайд

3 слайд
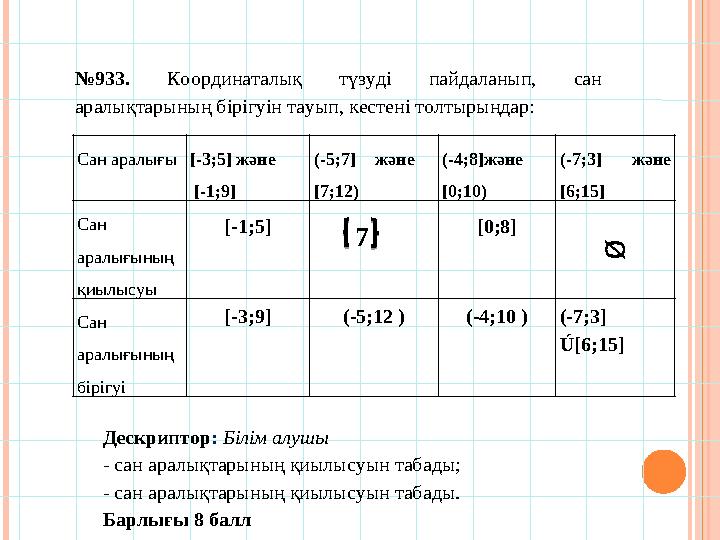
№ 933. Координаталық түзуді пайдаланып, сан аралықтарының бірігуін тауып, кестені толтырыңдар: Дескриптор : Білім алушы - сан аралықтарының қиылысуын табады; - сан аралықтарының қиылысуын табады. Барлы ғы 8 баллСан аралығы [-3;5] және [-1;9] (-5;7] және [7;12) (-4;8]және [0;10) (-7;3] және [6;15] Сан аралығының қиылысуы [-1;5] 7 [0;8] ᴓ Сан аралығының бірігуі [-3;9] (-5;12 ) (-4;10 ) (-7;3] Ú [6;15]

3 слайд

№ 933. Координаталық түзуді пайдаланып, сан аралықтарының бірігуін тауып, кестені толтырыңдар: Дескриптор : Білім алушы - сан аралықтарының қиылысуын табады; - сан аралықтарының қиылысуын табады. Барлы ғы 8 баллСан аралығы [-3;5] және [-1;9] (-5;7] және [7;12) (-4;8]және [0;10) (-7;3] және [6;15] Сан аралығының қиылысуы [-1;5] 7 [0;8] ᴓ Сан аралығының бірігуі [-3;9] (-5;12 ) (-4;10 ) (-7;3] Ú [6;15]

4 слайд
ӨТКЕНДІ ПЫСЫҚТАУ.  І топ  1. (-1; 3] [1; 5)= [1; 3)  2. (-3; 4] [1; 6]= (-3;6]  ІІ топ  1. (-2; 3] [1; 7)= [1; 3]  2. (-3;5] [-1; 8]= (-3; 8]  ІІІ топ  1. (-1;4] [1; 9)= [1 ; 4]  2. (-3; 5] [-1; 6]= (-3; 6]

4 слайд

ӨТКЕНДІ ПЫСЫҚТАУ.  І топ  1. (-1; 3] [1; 5)= [1; 3)  2. (-3; 4] [1; 6]= (-3;6]  ІІ топ  1. (-2; 3] [1; 7)= [1; 3]  2. (-3;5] [-1; 8]= (-3; 8]  ІІІ топ  1. (-1;4] [1; 9)= [1 ; 4]  2. (-3; 5] [-1; 6]= (-3; 6]

5 слайд
Қазақ халқының ұлы күйшілері

5 слайд

Қазақ халқының ұлы күйшілері

6 слайд

7 слайд
х 7 5 х

7 слайд

х 7 5 х

8 слайд
х х-3 1 Амангельдиева Д .

8 слайд

х х-3 1 Амангельдиева Д .

9 слайд
Бір айнымалысы бар сызықтық теңсіздік 5x-2<8; х-5>0; 3х+5>21-х – бір айнымалысы бар сызықтық теңсіздіктер. . Анықтама ax > b немесе ax < b түріндегі теңсіздіктер бір айнымалы сызықтық теңсіздіктер деп аталады, мұндағы а және b – кез келген сандар, а ≠ 0 . х – айнымалы Анықтама. Айнымалының теңсіздікті тура санды теңсіздікке айналдыратын мәнін бір айнымалысы бар сызықтық теңсіздіктің шешімі ( түбірі) деп атайды. Мысалы, x + 6 < 18 . х-тің орнына 2 мәнін қойсақ, онда 2+ 6 < 18 , 8 < 18 дұрыс теңсіздігін аламыз. х– теңсіздіктің шешімі ( түбірі) .

9 слайд

Бір айнымалысы бар сызықтық теңсіздік 5x-2<8; х-5>0; 3х+5>21-х – бір айнымалысы бар сызықтық теңсіздіктер. . Анықтама ax > b немесе ax < b түріндегі теңсіздіктер бір айнымалы сызықтық теңсіздіктер деп аталады, мұндағы а және b – кез келген сандар, а ≠ 0 . х – айнымалы Анықтама. Айнымалының теңсіздікті тура санды теңсіздікке айналдыратын мәнін бір айнымалысы бар сызықтық теңсіздіктің шешімі ( түбірі) деп атайды. Мысалы, x + 6 < 18 . х-тің орнына 2 мәнін қойсақ, онда 2+ 6 < 18 , 8 < 18 дұрыс теңсіздігін аламыз. х– теңсіздіктің шешімі ( түбірі) .

10 слайд
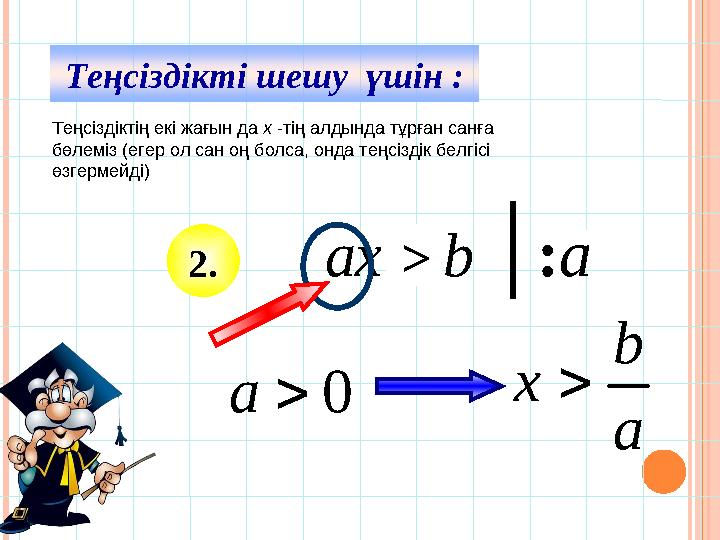
Теңсіздікті шешу үшін : 2 .b ax  < ≥≤> : а 0  a a b x Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз (егер ол сан оң болса, онда теңсіздік белгісі өзгермейді)

10 слайд

Теңсіздікті шешу үшін : 2 .b ax  < ≥≤> : а 0  a a b x Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз (егер ол сан оң болса, онда теңсіздік белгісі өзгермейді)

11 слайд
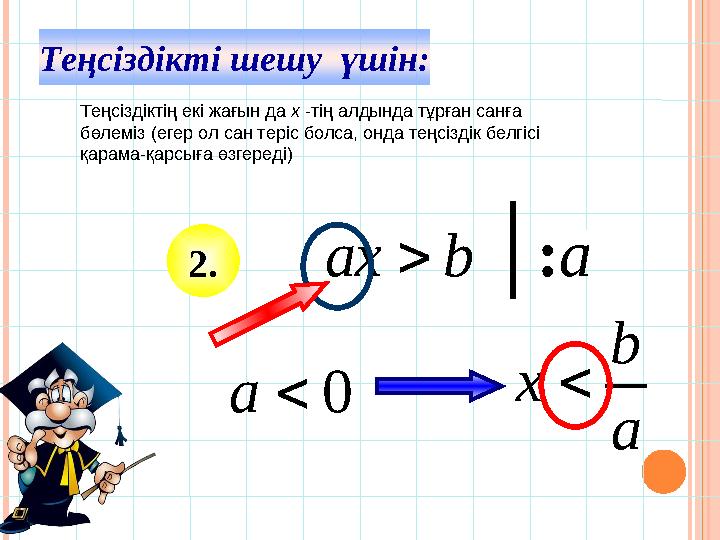
Теңсіздікті шешу үшін: 2 .b ax  : а 0  a a b x Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз (егер ол сан теріс болса, онда теңсіздік белгісі қарама-қарсыға өзгереді)

11 слайд

Теңсіздікті шешу үшін: 2 .b ax  : а 0  a a b x Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз (егер ол сан теріс болса, онда теңсіздік белгісі қарама-қарсыға өзгереді)

12 слайд
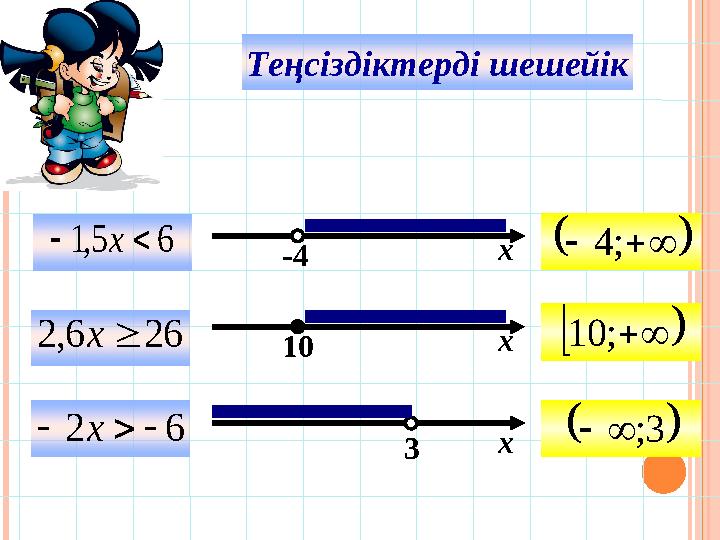
Теңсіздіктерді шешейік6 5, 1   х 6 2 6, 2  х 6 2    х х -4     ; 4    ; 10 х 10 3 х   3 ;  

12 слайд

Теңсіздіктерді шешейік6 5, 1   х 6 2 6, 2  х 6 2    х х -4     ; 4    ; 10 х 10 3 х   3 ;  

13 слайд
Мынадай теңсіздікті шешейік Ереже:c b ax   < ≥≤> b c ax  Теңсіздіктің сол жағын санды екінші жағына таңбасын ауыстырып көшіреміз.

13 слайд

Мынадай теңсіздікті шешейік Ереже:c b ax   < ≥≤> b c ax  Теңсіздіктің сол жағын санды екінші жағына таңбасын ауыстырып көшіреміз.

14 слайд
Теңсіздікті шешейік7 3 2 6    x x 2 7 3 6     x x 9 3   x 3   x -3 х Жауабы:   3 ;   

14 слайд

Теңсіздікті шешейік7 3 2 6    x x 2 7 3 6     x x 9 3   x 3   x -3 х Жауабы:   3 ;   

15 слайд
СЫНЫПТЫҚ ЖҰМЫС Сызықтық теңсіздіктерді шешу алгоритмі 15y + 3 ≤ 7 + 3y 1. Таңбаны қарама-қарсы таңбаға ауыстырып, х айнымалысы бар қосылғыштарды сол жаққа, ал сандарды оң жаққа орын ауыстыру. 2. Ұқсас мүшелерді біріктіру. 3. Теңсіздіктің екі жағын да х айнымалысының алдындағы санға (егер бұл сан оң сан болса, теңсіздік таңбасы өзгермейді, ал теріс сан болса, теңсіздік таңбасы қарама- қарсы таңбаға өзгереді) бөлу. 5. Аналитикалық түрінде берілген теңсіздікті геометриялық түрде бейнелеу. 6. Теңсіздікті қанағаттандыратын нүктелер жиынын жазу. Жауабы:

15 слайд

СЫНЫПТЫҚ ЖҰМЫС Сызықтық теңсіздіктерді шешу алгоритмі 15y + 3 ≤ 7 + 3y 1. Таңбаны қарама-қарсы таңбаға ауыстырып, х айнымалысы бар қосылғыштарды сол жаққа, ал сандарды оң жаққа орын ауыстыру. 2. Ұқсас мүшелерді біріктіру. 3. Теңсіздіктің екі жағын да х айнымалысының алдындағы санға (егер бұл сан оң сан болса, теңсіздік таңбасы өзгермейді, ал теріс сан болса, теңсіздік таңбасы қарама- қарсы таңбаға өзгереді) бөлу. 5. Аналитикалық түрінде берілген теңсіздікті геометриялық түрде бейнелеу. 6. Теңсіздікті қанағаттандыратын нүктелер жиынын жазу. Жауабы:

16 слайд
Топтық тапсырмалар

16 слайд

Топтық тапсырмалар

17 слайд
ТОПТЫҚ ЖҰМЫСТЫ БАҒАЛАУ  Барлық есепті дұрыс шығарған топқа:

17 слайд

ТОПТЫҚ ЖҰМЫСТЫ БАҒАЛАУ  Барлық есепті дұрыс шығарған топқа:

18 слайд
СЕРГІТУ  «А ққу»

18 слайд

СЕРГІТУ  «А ққу»

19 слайд
Досыңмен жұптас № 1 Тест. Теңсіздіктерді шеш. 1) 3x < 8 – x a) x > 2 b) x > 5 c) x > 3 d) x < 2 2) 4x – 3 <12 + x a) x < 2 b) x < 5 c) x > 3 d) x < 2 3) 5 + 4x > 20 – x a) x < 2 b) x > 3 c) x < 5 d) x < 2 4) 2(3 + x) > 18 – 4x a) x > 2 b) x < 5 c) x < 3 d) x < 2 № 2 Тест. Теңсіздіктерді шеш. 1) 2x < 9 – x a) x > 2 b) x > 5 c) x < 3 d) x < 2 2) 3x – 3 <11 + x a) x < 2 b) x < 5 c) x > 3 d) x < 7 3) 5 + 4x > 25 – x a) x < 2 b) x > 6 c) x < 6 d) x < 2 4) 2(3 + 2x) > 30 – 4x a) x > 3 b) x < 5 c) x < 3 d) x < 2 Тест жауаптары: № 1 1) d) x < 2; 2) b) x < 5; 3) b) x > 3; 4) a) x > 2 № 2 1) c) x < 3 2) d) x < 7; 3) b) x > 6; 4) a) x > 3 Бағалау: дұрыс жауап 1 балл

19 слайд

Досыңмен жұптас № 1 Тест. Теңсіздіктерді шеш. 1) 3x < 8 – x a) x > 2 b) x > 5 c) x > 3 d) x < 2 2) 4x – 3 <12 + x a) x < 2 b) x < 5 c) x > 3 d) x < 2 3) 5 + 4x > 20 – x a) x < 2 b) x > 3 c) x < 5 d) x < 2 4) 2(3 + x) > 18 – 4x a) x > 2 b) x < 5 c) x < 3 d) x < 2 № 2 Тест. Теңсіздіктерді шеш. 1) 2x < 9 – x a) x > 2 b) x > 5 c) x < 3 d) x < 2 2) 3x – 3 <11 + x a) x < 2 b) x < 5 c) x > 3 d) x < 7 3) 5 + 4x > 25 – x a) x < 2 b) x > 6 c) x < 6 d) x < 2 4) 2(3 + 2x) > 30 – 4x a) x > 3 b) x < 5 c) x < 3 d) x < 2 Тест жауаптары: № 1 1) d) x < 2; 2) b) x < 5; 3) b) x > 3; 4) a) x > 2 № 2 1) c) x < 3 2) d) x < 7; 3) b) x > 6; 4) a) x > 3 Бағалау: дұрыс жауап 1 балл

20 слайд
БҮГІНГІ САБАҚТАН НЕ ҮЙРЕНДІК?  Жеке жұмыс  Теңсіздікті шешіңіздер:  2х+1>0.  Теңсіздікті шешіңіздер:   Теңсіздікті шешіңіздер: 

20 слайд

БҮГІНГІ САБАҚТАН НЕ ҮЙРЕНДІК?  Жеке жұмыс  Теңсіздікті шешіңіздер:  2х+1>0.  Теңсіздікті шешіңіздер:   Теңсіздікті шешіңіздер: 

21 слайд
ДЕСКРИПТОР: 1 Санның таңбасын қарама-қарсы таңбаға ауыстырып теңсіздік екінші жағына көшіреді. Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз 1 Аналитикалық түрінде берілген теңсіздікті геометриялық түрде бейнелейді, жауабын жазады, 1 2 x -і бар қосылғыштарды теңсіздіктің бір жағына, ал сандарды екінші жағына таңбаларын ауыстырып көшіреді 1 Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз 1 Аналитикалық түрінде берілген теңсіздікті геометриялық түрде бейнелейді, жауабын жазады, 1 3 Жақшаны ашамыз. 1 x -і бар қосылғыштарды теңсіздіктің бір жағына, ал сандарды екінші жағына таңбаларын ауыстырып көшіреміз. 1 Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз 1 Аналитикалық түрінде берілген теңсіздікті геометриялық түрде бейнелейді және жауабын жазады 1 .Жалпы балл 9 балл

21 слайд

ДЕСКРИПТОР: 1 Санның таңбасын қарама-қарсы таңбаға ауыстырып теңсіздік екінші жағына көшіреді. Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз 1 Аналитикалық түрінде берілген теңсіздікті геометриялық түрде бейнелейді, жауабын жазады, 1 2 x -і бар қосылғыштарды теңсіздіктің бір жағына, ал сандарды екінші жағына таңбаларын ауыстырып көшіреді 1 Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз 1 Аналитикалық түрінде берілген теңсіздікті геометриялық түрде бейнелейді, жауабын жазады, 1 3 Жақшаны ашамыз. 1 x -і бар қосылғыштарды теңсіздіктің бір жағына, ал сандарды екінші жағына таңбаларын ауыстырып көшіреміз. 1 Теңсіздіктің екі жағын да x -тің алдында тұрған санға бөлеміз 1 Аналитикалық түрінде берілген теңсіздікті геометриялық түрде бейнелейді және жауабын жазады 1 .Жалпы балл 9 балл

22 слайд
ҚОРЫТЫНДЫ  Үй жұмысы: №943  Рефлексия

22 слайд

ҚОРЫТЫНДЫ  Үй жұмысы: №943  Рефлексия

23 слайд
Ән «Құстар әні»

23 слайд

Ән «Құстар әні»