Материалдар / Квадрат теңсіздіктер. 8-сынып

Квадрат теңсіздіктер. 8-сынып

Материал туралы қысқаша түсінік

Математика пәнінің мұғалімдеріне қажет. Ашық сабақтарға, бекіту сабағына қолдануға болады.

Оган Орнек

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

15 Қараша 2020

1028

0 рет жүктелген

Алгебра Презентация 8 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 15

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
АА қмола облысы қмола облысы Целиноград ауданы Целиноград ауданы Қоянды орта Қоянды орта мектебінің мектебінің математика пәнінің математика пәнінің мұғалімімұғалімі Оган ОрнекОган Орнек

1 слайд

АА қмола облысы қмола облысы Целиноград ауданы Целиноград ауданы Қоянды орта Қоянды орта мектебінің мектебінің математика пәнінің математика пәнінің мұғалімімұғалімі Оган ОрнекОган Орнек

2 слайд
САБАҚТЫҢ ТАҚЫРЫБЫСАБАҚТЫҢ ТАҚЫРЫБЫ  Оқу мақсаты: Оқу мақсаты: 8.2.2.9 Рационал т8.2.2.9 Рационал т еңсіздіктер. Интервалдар әдісі. еңсіздіктер. Интервалдар әдісі.  Сабақ мақсаты:Сабақ мақсаты: Теңсіздіктерді интервалдар әдісімен шешу. Теңсіздіктерді интервалдар әдісімен шешу. Теңсіздіктерді шешуде интервалдар әдісінің алгоритмін Теңсіздіктерді шешуде интервалдар әдісінің алгоритмін қолдану және рационал теңсіздіктерде бөгде қолдану және рационал теңсіздіктерде бөгде түбірлерді анықтау.түбірлерді анықтау.  ТТ ілдік мақсат:ілдік мақсат: Берілген есептердің шартына сәйкес шешу алгоритмін Берілген есептердің шартына сәйкес шешу алгоритмін сипаттайды. Бөлім бойынша лексика мен сипаттайды. Бөлім бойынша лексика мен терминологияны сабақ барысында қолданады. терминологияны сабақ барысында қолданады.  Бағалау критерийлері:Бағалау критерийлері: Теңсіздіктерді интервалдар әдісімен шешу алгоритмін Теңсіздіктерді интервалдар әдісімен шешу алгоритмін тұжырымдайды. Координаталық түзуде аралықтарды тұжырымдайды. Координаталық түзуде аралықтарды бөліп, таңбаларын анықтай алады. Рационал бөліп, таңбаларын анықтай алады. Рационал теңсіздікті шешуде бөгде түбірлерді ерекшелейді теңсіздікті шешуде бөгде түбірлерді ерекшелейді және есептің шартына сәйкес қанағаттандыратын және есептің шартына сәйкес қанағаттандыратын жауаптарды табады. Есептің жауабын жаза алады. жауаптарды табады. Есептің жауабын жаза алады. 8.4А 8.4А Квадрат теңсіздіктерКвадрат теңсіздіктер

2 слайд

САБАҚТЫҢ ТАҚЫРЫБЫСАБАҚТЫҢ ТАҚЫРЫБЫ  Оқу мақсаты: Оқу мақсаты: 8.2.2.9 Рационал т8.2.2.9 Рационал т еңсіздіктер. Интервалдар әдісі. еңсіздіктер. Интервалдар әдісі.  Сабақ мақсаты:Сабақ мақсаты: Теңсіздіктерді интервалдар әдісімен шешу. Теңсіздіктерді интервалдар әдісімен шешу. Теңсіздіктерді шешуде интервалдар әдісінің алгоритмін Теңсіздіктерді шешуде интервалдар әдісінің алгоритмін қолдану және рационал теңсіздіктерде бөгде қолдану және рационал теңсіздіктерде бөгде түбірлерді анықтау.түбірлерді анықтау.  ТТ ілдік мақсат:ілдік мақсат: Берілген есептердің шартына сәйкес шешу алгоритмін Берілген есептердің шартына сәйкес шешу алгоритмін сипаттайды. Бөлім бойынша лексика мен сипаттайды. Бөлім бойынша лексика мен терминологияны сабақ барысында қолданады. терминологияны сабақ барысында қолданады.  Бағалау критерийлері:Бағалау критерийлері: Теңсіздіктерді интервалдар әдісімен шешу алгоритмін Теңсіздіктерді интервалдар әдісімен шешу алгоритмін тұжырымдайды. Координаталық түзуде аралықтарды тұжырымдайды. Координаталық түзуде аралықтарды бөліп, таңбаларын анықтай алады. Рационал бөліп, таңбаларын анықтай алады. Рационал теңсіздікті шешуде бөгде түбірлерді ерекшелейді теңсіздікті шешуде бөгде түбірлерді ерекшелейді және есептің шартына сәйкес қанағаттандыратын және есептің шартына сәйкес қанағаттандыратын жауаптарды табады. Есептің жауабын жаза алады. жауаптарды табады. Есептің жауабын жаза алады. 8.4А 8.4А Квадрат теңсіздіктерКвадрат теңсіздіктер

3 слайд
Квадрат Квадрат теңсіздіктерді теңсіздіктерді шешудің негізгі екі шешудің негізгі екі әдісі барәдісі бар :: 1. 1. Квадраттық Квадраттық функцияның графигі функцияның графигі арқылы шығаруарқылы шығару 2. Интервалдар әдісі 2. Интервалдар әдісі арқылы шығаруарқылы шығару Еске түсірейік!Еске түсірейік! Квадрат теңсіздікті графиктік әдісімен Квадрат теңсіздікті графиктік әдісімен шешу үшін:шешу үшін: у=аху=ах 22 + + bxbx + + cc функциясын қарастырамыз функциясын қарастырамыз 1.1. Функция нөлдерін табамыз.Функция нөлдерін табамыз. 2.2. Парабола тармақтарының бағытын анықтаймыз.Парабола тармақтарының бағытын анықтаймыз. 3.3. Функция графигін кескіндейміз.Функция графигін кескіндейміз. 4.4. Теңсіздік таңбасына қарай жауаптарын жазамыз. Теңсіздік таңбасына қарай жауаптарын жазамыз.

3 слайд

Квадрат Квадрат теңсіздіктерді теңсіздіктерді шешудің негізгі екі шешудің негізгі екі әдісі барәдісі бар :: 1. 1. Квадраттық Квадраттық функцияның графигі функцияның графигі арқылы шығаруарқылы шығару 2. Интервалдар әдісі 2. Интервалдар әдісі арқылы шығаруарқылы шығару Еске түсірейік!Еске түсірейік! Квадрат теңсіздікті графиктік әдісімен Квадрат теңсіздікті графиктік әдісімен шешу үшін:шешу үшін: у=аху=ах 22 + + bxbx + + cc функциясын қарастырамыз функциясын қарастырамыз 1.1. Функция нөлдерін табамыз.Функция нөлдерін табамыз. 2.2. Парабола тармақтарының бағытын анықтаймыз.Парабола тармақтарының бағытын анықтаймыз. 3.3. Функция графигін кескіндейміз.Функция графигін кескіндейміз. 4.4. Теңсіздік таңбасына қарай жауаптарын жазамыз. Теңсіздік таңбасына қарай жауаптарын жазамыз.

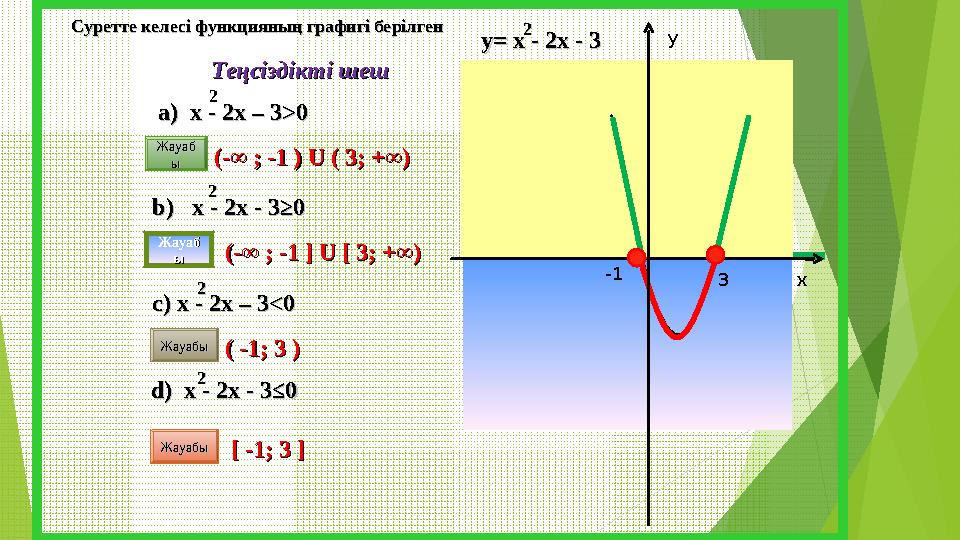
4 слайд
y xу= х - 2х - 3у= х - 2х - 3 2 2 Теңсіздікті шешТеңсіздікті шешСуретте келесі функцияның графигі берілгенСуретте келесі функцияның графигі берілген a) a) х - 2х – 3 х - 2х – 3 >0>022 b) b) х - 2х - 3≥х - 2х - 3≥ 0022 cc ) х - 2х – 3) х - 2х – 3 <0 <0 22 dd ) х - 2х - 3≤0 ) х - 2х - 3≤0 22 ЖауабЖауаб ыы (-∞ (-∞ ; -1 ) ; -1 ) UU ( 3 ( 3 ; ; +∞)+∞) ЖауабЖауаб ыы [ -1[ -1 ; 3 ; 3 ]]ЖауабыЖауабы (( -1 -1 ; 3 ); 3 ) Жауабы Жауабы (-∞ (-∞ ; -1 ; -1 ]] UU [[ 3 3 ;; +∞) +∞) -1 3

4 слайд

y xу= х - 2х - 3у= х - 2х - 3 2 2 Теңсіздікті шешТеңсіздікті шешСуретте келесі функцияның графигі берілгенСуретте келесі функцияның графигі берілген a) a) х - 2х – 3 х - 2х – 3 >0>022 b) b) х - 2х - 3≥х - 2х - 3≥ 0022 cc ) х - 2х – 3) х - 2х – 3 <0 <0 22 dd ) х - 2х - 3≤0 ) х - 2х - 3≤0 22 ЖауабЖауаб ыы (-∞ (-∞ ; -1 ) ; -1 ) UU ( 3 ( 3 ; ; +∞)+∞) ЖауабЖауаб ыы [ -1[ -1 ; 3 ; 3 ]]ЖауабыЖауабы (( -1 -1 ; 3 ); 3 ) Жауабы Жауабы (-∞ (-∞ ; -1 ; -1 ]] UU [[ 3 3 ;; +∞) +∞) -1 3

5 слайд
Квадрат Квадрат теңсіздіктердтеңсіздіктерд і шешудің і шешудің негізгі екі негізгі екі әдісі барәдісі бар :: 1. 1. Квадраттық Квадраттық функцияның функцияның графигі арқылы графигі арқылы шығарушығару 2. Интервалдар 2. Интервалдар әдісі арқылы әдісі арқылы шығарушығару Еске Еске сақтайықсақтайық !! Квадрат теңсіздікті интервалдар әдісімен шешу Квадрат теңсіздікті интервалдар әдісімен шешу үшін:үшін: у= аху= ах 22 + + bxbx + + cc функциясын қарастырамыз функциясын қарастырамыз 1.1. Функция нөлдерін табамыз.Функция нөлдерін табамыз. 2.2. Сан тСан т үзуінде функция нөлдерін (нүктелерді) белгілейміз. үзуінде функция нөлдерін (нүктелерді) белгілейміз. 3.3. Белгіленген нүктелер арқылы сан түзуін аралықтарға бөлеміз. Белгіленген нүктелер арқылы сан түзуін аралықтарға бөлеміз. 4.4. Оң жақ шетінен бастап аралықтардың таңбасын анықтаймыз. Оң жақ шетінен бастап аралықтардың таңбасын анықтаймыз. (егер (егер xx 0 0 саны тақ рет қайталанған жағдайда аралық таңбалары саны тақ рет қайталанған жағдайда аралық таңбалары кезекпен қойылады, ал жұп рет қайталанған жағдайда осы кезекпен қойылады, ал жұп рет қайталанған жағдайда осы мәннің екі жағындағы аралықтардың таңбалары бірдей етіп мәннің екі жағындағы аралықтардың таңбалары бірдей етіп қойыладықойылады )) 5.5. Берілген теңсіздіктің таңбасына қарай жауаптарын жазамыз.Берілген теңсіздіктің таңбасына қарай жауаптарын жазамыз.

5 слайд

Квадрат Квадрат теңсіздіктердтеңсіздіктерд і шешудің і шешудің негізгі екі негізгі екі әдісі барәдісі бар :: 1. 1. Квадраттық Квадраттық функцияның функцияның графигі арқылы графигі арқылы шығарушығару 2. Интервалдар 2. Интервалдар әдісі арқылы әдісі арқылы шығарушығару Еске Еске сақтайықсақтайық !! Квадрат теңсіздікті интервалдар әдісімен шешу Квадрат теңсіздікті интервалдар әдісімен шешу үшін:үшін: у= аху= ах 22 + + bxbx + + cc функциясын қарастырамыз функциясын қарастырамыз 1.1. Функция нөлдерін табамыз.Функция нөлдерін табамыз. 2.2. Сан тСан т үзуінде функция нөлдерін (нүктелерді) белгілейміз. үзуінде функция нөлдерін (нүктелерді) белгілейміз. 3.3. Белгіленген нүктелер арқылы сан түзуін аралықтарға бөлеміз. Белгіленген нүктелер арқылы сан түзуін аралықтарға бөлеміз. 4.4. Оң жақ шетінен бастап аралықтардың таңбасын анықтаймыз. Оң жақ шетінен бастап аралықтардың таңбасын анықтаймыз. (егер (егер xx 0 0 саны тақ рет қайталанған жағдайда аралық таңбалары саны тақ рет қайталанған жағдайда аралық таңбалары кезекпен қойылады, ал жұп рет қайталанған жағдайда осы кезекпен қойылады, ал жұп рет қайталанған жағдайда осы мәннің екі жағындағы аралықтардың таңбалары бірдей етіп мәннің екі жағындағы аралықтардың таңбалары бірдей етіп қойыладықойылады )) 5.5. Берілген теңсіздіктің таңбасына қарай жауаптарын жазамыз.Берілген теңсіздіктің таңбасына қарай жауаптарын жазамыз.

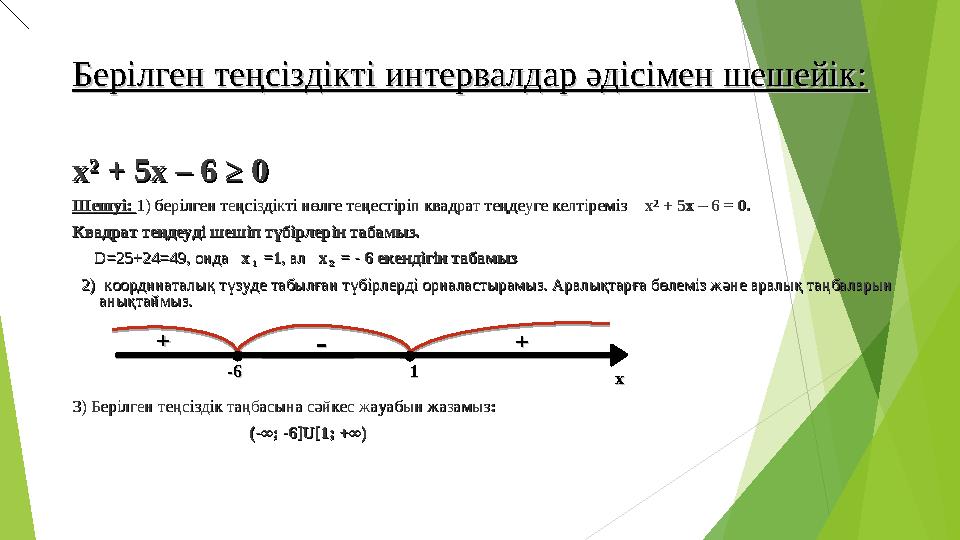
6 слайд
Берілген теңсіздікті интервалдар әдісімен шешейік:Берілген теңсіздікті интервалдар әдісімен шешейік: хх ²² + 5х – 6 ≥ 0 + 5х – 6 ≥ 0 Шешуі: Шешуі: 1) берілген теңсіздікті нөлге теңестіріп квадрат теңдеуге келтіреміз 1) берілген теңсіздікті нөлге теңестіріп квадрат теңдеуге келтіреміз хх ²² + 5х – 6 = 0. + 5х – 6 = 0. Квадрат теңдеуді шешіп түбірлерін табамыз. Квадрат теңдеуді шешіп түбірлерін табамыз. D=25+24=49D=25+24=49 , , онда онда х₁ =1х₁ =1 , ал , ал х₂ = - 6 екендігін табамызх₂ = - 6 екендігін табамыз 2) координаталық түзуде табылған түбірлерді орналастырамыз. Аралықтарға бөлеміз және аралық таңбаларын 2) координаталық түзуде табылған түбірлерді орналастырамыз. Аралықтарға бөлеміз және аралық таңбаларын анықтаймыз.анықтаймыз. 3) Берілген теңсіздік таңбасына сәйкес жауабын жазамыз3) Берілген теңсіздік таңбасына сәйкес жауабын жазамыз : : (-∞; -6(-∞; -6 ]U[]U[ 1; +∞)1; +∞)++ -- ++ -6-6 11 xx

6 слайд

Берілген теңсіздікті интервалдар әдісімен шешейік:Берілген теңсіздікті интервалдар әдісімен шешейік: хх ²² + 5х – 6 ≥ 0 + 5х – 6 ≥ 0 Шешуі: Шешуі: 1) берілген теңсіздікті нөлге теңестіріп квадрат теңдеуге келтіреміз 1) берілген теңсіздікті нөлге теңестіріп квадрат теңдеуге келтіреміз хх ²² + 5х – 6 = 0. + 5х – 6 = 0. Квадрат теңдеуді шешіп түбірлерін табамыз. Квадрат теңдеуді шешіп түбірлерін табамыз. D=25+24=49D=25+24=49 , , онда онда х₁ =1х₁ =1 , ал , ал х₂ = - 6 екендігін табамызх₂ = - 6 екендігін табамыз 2) координаталық түзуде табылған түбірлерді орналастырамыз. Аралықтарға бөлеміз және аралық таңбаларын 2) координаталық түзуде табылған түбірлерді орналастырамыз. Аралықтарға бөлеміз және аралық таңбаларын анықтаймыз.анықтаймыз. 3) Берілген теңсіздік таңбасына сәйкес жауабын жазамыз3) Берілген теңсіздік таңбасына сәйкес жауабын жазамыз : : (-∞; -6(-∞; -6 ]U[]U[ 1; +∞)1; +∞)++ -- ++ -6-6 11 xx

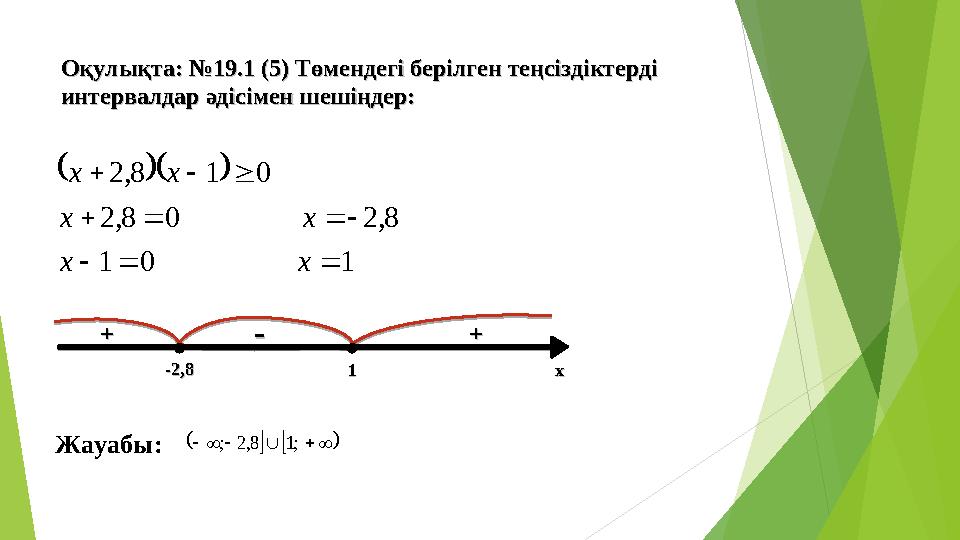
7 слайд
Оқулықта: №Оқулықта: № 19.1 (5) 19.1 (5) Төмендегі берілген теңсіздіктерді Төмендегі берілген теңсіздіктерді интервалдар әдісімен шешіңдер:интервалдар әдісімен шешіңдер:    1 0 1 8, 2 0 8, 2 0 1 8, 2           x x x x x x ++ -- ++ -2,8-2,8 11 xx Жауабы:           ;1 8,2 ;

7 слайд

Оқулықта: №Оқулықта: № 19.1 (5) 19.1 (5) Төмендегі берілген теңсіздіктерді Төмендегі берілген теңсіздіктерді интервалдар әдісімен шешіңдер:интервалдар әдісімен шешіңдер:    1 0 1 8, 2 0 8, 2 0 1 8, 2           x x x x x x ++ -- ++ -2,8-2,8 11 xx Жауабы:           ;1 8,2 ;

8 слайд
Оқулықта: №Оқулықта: № 19.1 (8) 19.1 (8) Төмендегі берілген теңсіздіктерді Төмендегі берілген теңсіздіктерді интервалдар әдісімен шешіңдер:интервалдар әдісімен шешіңдер:   5, 3 0 5, 3 7 0 7 0 5, 3 7           x x x x x x Жауабы:           ;5,3 7 ;++ -- ++ -7-7 3,53,5 xx

8 слайд

Оқулықта: №Оқулықта: № 19.1 (8) 19.1 (8) Төмендегі берілген теңсіздіктерді Төмендегі берілген теңсіздіктерді интервалдар әдісімен шешіңдер:интервалдар әдісімен шешіңдер:   5, 3 0 5, 3 7 0 7 0 5, 3 7           x x x x x x Жауабы:           ;5,3 7 ;++ -- ++ -7-7 3,53,5 xx

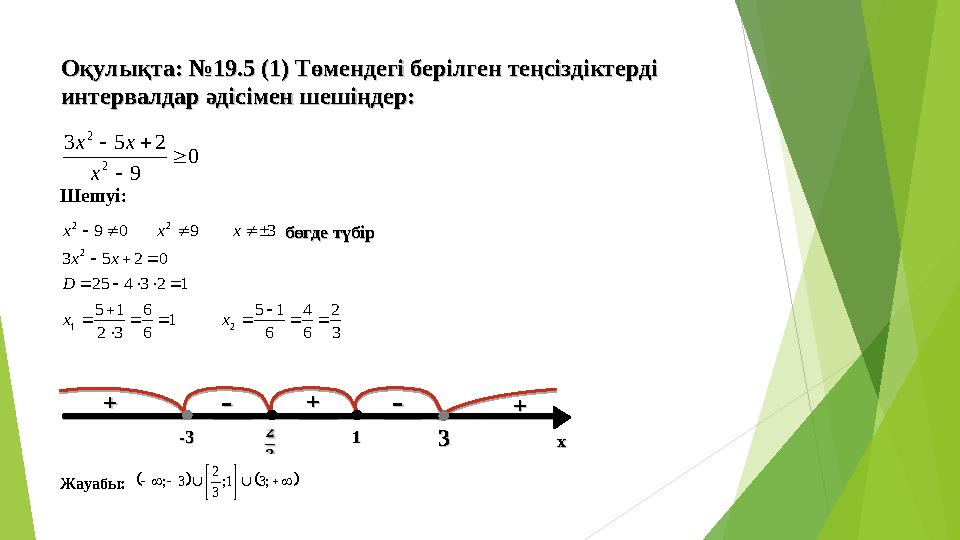
9 слайд
Оқулықта: №Оқулықта: № 19.5 (19.5 ( 11 ) ) Төмендегі берілген теңсіздіктерді Төмендегі берілген теңсіздіктерді интервалдар әдісімен шешіңдер:интервалдар әдісімен шешіңдер:0 9 2 5 3 2 2     x x x Шешуі: 3 2 6 4 6 1 5 1 6 6 3 2 1 5 1 2 3 4 25 0 2 5 3 3 9 0 9 2 1 2 2 2                       x x D x x x x x -- --++ ++++ -3-3 11 33 Жауабы:               ;3 1; 3 2 3 ; xxбөгде түбірбөгде түбір

9 слайд

Оқулықта: №Оқулықта: № 19.5 (19.5 ( 11 ) ) Төмендегі берілген теңсіздіктерді Төмендегі берілген теңсіздіктерді интервалдар әдісімен шешіңдер:интервалдар әдісімен шешіңдер:0 9 2 5 3 2 2     x x x Шешуі: 3 2 6 4 6 1 5 1 6 6 3 2 1 5 1 2 3 4 25 0 2 5 3 3 9 0 9 2 1 2 2 2                       x x D x x x x x -- --++ ++++ -3-3 11 33 Жауабы:               ;3 1; 3 2 3 ; xxбөгде түбірбөгде түбір

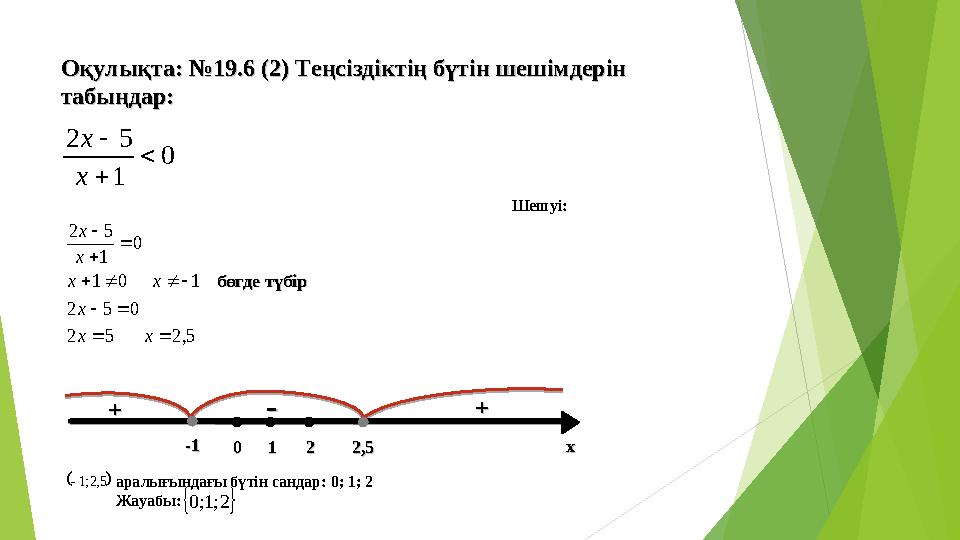
10 слайд
Оқулықта: №Оқулықта: № 19.19. 66 ( ( 22 ) Теңсіздіктің бүтін шешімдерін ) Теңсіздіктің бүтін шешімдерін табыңдартабыңдар ::0 1 5 2    x x Шешуі: 5,2 5 2 0 5 2 1 0 1 0 1 5 2            x x x x x x x ++ ++ -- -1-1 00 11 2,52,5 22 xx  5,2;1  2;1;0 аралығындағы бүтін сандар: 0 ; 1; 2 Жауабы: бөгде түбірбөгде түбір

10 слайд

Оқулықта: №Оқулықта: № 19.19. 66 ( ( 22 ) Теңсіздіктің бүтін шешімдерін ) Теңсіздіктің бүтін шешімдерін табыңдартабыңдар ::0 1 5 2    x x Шешуі: 5,2 5 2 0 5 2 1 0 1 0 1 5 2            x x x x x x x ++ ++ -- -1-1 00 11 2,52,5 22 xx  5,2;1  2;1;0 аралығындағы бүтін сандар: 0 ; 1; 2 Жауабы: бөгде түбірбөгде түбір

11 слайд
«Иә» немесе «Жоқ»«Иә» немесе «Жоқ» 1.1. Квадрат теңсіздіктің жалпы түрі т.с.с. түрінде беріледі.Квадрат теңсіздіктің жалпы түрі т.с.с. түрінде беріледі. 2.2. Квадрат теңсіздіктің графигі гипербола деп аталады.Квадрат теңсіздіктің графигі гипербола деп аталады. 3.3. Квадрат теңсіздікте Квадрат теңсіздікте a>0 a>0 болған жағдайда парабола тармағы жоғары қарайды.болған жағдайда парабола тармағы жоғары қарайды. 4.4. Квадрат теңсіздікте Квадрат теңсіздікте D>0 D>0 болса, парабола болса, парабола OX OX осімен бір нүктеде қиылысады.осімен бір нүктеде қиылысады. 5.5. функциясы графигінің функциясы графигінің OX OX осімен қиылысу нүктесінің абсциссаларын – осімен қиылысу нүктесінің абсциссаларын – функцияның нөлдері деп атайды.функцияның нөлдері деп атайды. 6.6. x< -4 x< -4 теңсіздігін аралықпен жазсақ теңсіздігін аралықпен жазсақ болады. болады. 7.7. Квадрат және бөлшек рационал теңсіздіктерді интервалдар әдісімен шешуге Квадрат және бөлшек рационал теңсіздіктерді интервалдар әдісімен шешуге болады.болады. 8.8. Квадрат теңсіздікте Квадрат теңсіздікте a<0 a<0 болған жағдайда парабола тармағы жоғары қарайды.болған жағдайда парабола тармағы жоғары қарайды.0 ,0 2     a c bx ax c bx ax y    2  4 ;  

11 слайд

«Иә» немесе «Жоқ»«Иә» немесе «Жоқ» 1.1. Квадрат теңсіздіктің жалпы түрі т.с.с. түрінде беріледі.Квадрат теңсіздіктің жалпы түрі т.с.с. түрінде беріледі. 2.2. Квадрат теңсіздіктің графигі гипербола деп аталады.Квадрат теңсіздіктің графигі гипербола деп аталады. 3.3. Квадрат теңсіздікте Квадрат теңсіздікте a>0 a>0 болған жағдайда парабола тармағы жоғары қарайды.болған жағдайда парабола тармағы жоғары қарайды. 4.4. Квадрат теңсіздікте Квадрат теңсіздікте D>0 D>0 болса, парабола болса, парабола OX OX осімен бір нүктеде қиылысады.осімен бір нүктеде қиылысады. 5.5. функциясы графигінің функциясы графигінің OX OX осімен қиылысу нүктесінің абсциссаларын – осімен қиылысу нүктесінің абсциссаларын – функцияның нөлдері деп атайды.функцияның нөлдері деп атайды. 6.6. x< -4 x< -4 теңсіздігін аралықпен жазсақ теңсіздігін аралықпен жазсақ болады. болады. 7.7. Квадрат және бөлшек рационал теңсіздіктерді интервалдар әдісімен шешуге Квадрат және бөлшек рационал теңсіздіктерді интервалдар әдісімен шешуге болады.болады. 8.8. Квадрат теңсіздікте Квадрат теңсіздікте a<0 a<0 болған жағдайда парабола тармағы жоғары қарайды.болған жағдайда парабола тармағы жоғары қарайды.0 ,0 2     a c bx ax c bx ax y    2  4 ;  

12 слайд
Жауаптары:Жауаптары: 1.1. ИәИә 2.2. ЖоқЖоқ 3.3. ИәИә 4.4. ЖоқЖоқ 5.5. ИәИә 6.6. ИәИә 7.7. ИәИә 8.8. ЖоқЖоқ

12 слайд

Жауаптары:Жауаптары: 1.1. ИәИә 2.2. ЖоқЖоқ 3.3. ИәИә 4.4. ЖоқЖоқ 5.5. ИәИә 6.6. ИәИә 7.7. ИәИә 8.8. ЖоқЖоқ

13 слайд
Үйге: оқулықта 1 49 -15 0 б . , № 19.1, 19. 5 , 19. 6 Рефлексия. 1. Саба қ мен үшін ..... көрінді қысқа / ұзақ 2. Мен сабақта …. шаршамадым / шаршадым 3. Менің көңіл күйім…. керемет / онша емес 4. Сабақ маған … болды. түсінікті / түсініксіз пайдалы / пайдасыз қызықты / қызықсыз 1. Үй тапсырмасы ...... сияқты. жеңіл / қиын қызықты / қызықсыз

13 слайд

Үйге: оқулықта 1 49 -15 0 б . , № 19.1, 19. 5 , 19. 6 Рефлексия. 1. Саба қ мен үшін ..... көрінді қысқа / ұзақ 2. Мен сабақта …. шаршамадым / шаршадым 3. Менің көңіл күйім…. керемет / онша емес 4. Сабақ маған … болды. түсінікті / түсініксіз пайдалы / пайдасыз қызықты / қызықсыз 1. Үй тапсырмасы ...... сияқты. жеңіл / қиын қызықты / қызықсыз

14 слайд
Барлықтарыңызға рахмет!

14 слайд

Барлықтарыңызға рахмет!