Материалдар / Математикалық сайыс

Математикалық сайыс

Материал туралы қысқаша түсінік

жас мамандарға көмегі тиері хақ

Тулеева Жанар Закировна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

09 Сәуір 2019

868

0 рет жүктелген

Математика Презентация 10 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 13

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд
Мақсаты: Оқушылардың алған білімдерін одан әрі тереңдету, шапшаң ойлауға, әр іске логикасы мықты болуға бейімдеу. Ұранымыз: Білімдіге – биіктен орын!

2 слайд

Мақсаты: Оқушылардың алған білімдерін одан әрі тереңдету, шапшаң ойлауға, әр іске логикасы мықты болуға бейімдеу. Ұранымыз: Білімдіге – биіктен орын!

3 слайд
Өту жоспары: I-бөлім Танымдық деңгей – Сен білесің бе? (Сұрақтар) Алгоритмдік деңгей – Формулаларды жалғастыр Эвристикалық деңгей – Кім жылдам? (жедел-тест) Шығармашылық деңгей – Жоба қорғау. II-бөлім «Қазақтың кемеңгер математиктерінің жолы – бізге үлгі» атты әдеби монтаж.

3 слайд

Өту жоспары: I-бөлім Танымдық деңгей – Сен білесің бе? (Сұрақтар) Алгоритмдік деңгей – Формулаларды жалғастыр Эвристикалық деңгей – Кім жылдам? (жедел-тест) Шығармашылық деңгей – Жоба қорғау. II-бөлім «Қазақтың кемеңгер математиктерінің жолы – бізге үлгі» атты әдеби монтаж.

4 слайд
«Адамның ақыл – ойының кеңейе түсуіне математиканың тигізетін әсерін айтып жеткізу қиын. Математика ой, ақыл шегін кеңейтеді» (О.А.Жәутіков)

4 слайд

«Адамның ақыл – ойының кеңейе түсуіне математиканың тигізетін әсерін айтып жеткізу қиын. Математика ой, ақыл шегін кеңейтеді» (О.А.Жәутіков)

5 слайд
Сен білесің бе? 1) Үшбұрыштың үш қабырғасы берілген: 6см,8см,10см. Үшбұрыштың түрін анықтаңыз. А) доғал бұрышты, С) тең бүйірлі доғал Е) сүйір бұрышты В) тік бұрышты, Д)тең бүйірлі сүйір бұрышты 2) Сөйлемді толықтырыңыз: «Кез – келген тақ функцияның графигі ... .... . қатысты симметриялы». А) координатор басына; С) ордината осіне; Е) абцисса осіне В) ОУ оң жарты осіне; Д) ОХ оң жарты осіне; 3) Анықтаманы толықтырыңыз: « ... айнымалының қабылдайтын барлық мәндері функцияның анықталу облысын құрайды.» А) тәуелсіз В) белгілі С) тәуелді Д) белгісіз Е) сәйкес 4) Жұп функцияны анықтаңыз:x cos2x y Ä) x sin2x y B) x sin2x y E) x cos2x y C) x cos2x y À) 2 3 2           5) Тақ функцияны анықтаңыз: 2 2 2 2 x x/x/ y Ä) x - x/x/ y B) x /x/ x y E) x x/x/ y C) x -x/x/ y A)          В А А А С

5 слайд

Сен білесің бе? 1) Үшбұрыштың үш қабырғасы берілген: 6см,8см,10см. Үшбұрыштың түрін анықтаңыз. А) доғал бұрышты, С) тең бүйірлі доғал Е) сүйір бұрышты В) тік бұрышты, Д)тең бүйірлі сүйір бұрышты 2) Сөйлемді толықтырыңыз: «Кез – келген тақ функцияның графигі ... .... . қатысты симметриялы». А) координатор басына; С) ордината осіне; Е) абцисса осіне В) ОУ оң жарты осіне; Д) ОХ оң жарты осіне; 3) Анықтаманы толықтырыңыз: « ... айнымалының қабылдайтын барлық мәндері функцияның анықталу облысын құрайды.» А) тәуелсіз В) белгілі С) тәуелді Д) белгісіз Е) сәйкес 4) Жұп функцияны анықтаңыз:x cos2x y Ä) x sin2x y B) x sin2x y E) x cos2x y C) x cos2x y À) 2 3 2           5) Тақ функцияны анықтаңыз: 2 2 2 2 x x/x/ y Ä) x - x/x/ y B) x /x/ x y E) x x/x/ y C) x -x/x/ y A)          В А А А С

6 слайд
1) Тікбұрышты үшбұрыштың ауданы оның ... А) табаны мен сәйкес биіктігі көбейтіндісінің жартысына тең; В) табандарының жарты қосындысы мен биіктігінің көбейтіндісіне тең; С) катеттері көбейтіндісінің жартысына тең; Д) іргелес жатқан екі қабырғасының көбейтіндісіне тең; Е) табаны мен биіктігінің көбейтіндісіне тең; 2) Пифагор өрнектейтін теорема ... А) тікбұрышты үшбұрыштың бұрыштарын ; В) тікбұрышты үшбұрыштың қабырғаларының арасындағы қатынасты ; С) тікбұрышты үшбұрыштың гипотенузасын ; Д) кез – келген үшбұрыштың қабырғаларын; Е) тең бүйірлі үшбұрыштың бұрыштарын . 3) y = ax + b функциясының графигі А) түзу В) шеңбер С) парабола Д) гипербола Е) кубтық парабола 4) y = ax + bx + c квадраттық функцияның анықталу облысы А) барлық нақты сандар ( R ) жиыны Д) натурал сандар жиыны В) рационал сандар ( Q ) жиыны Е) иррационал сандар жиыны С) бүтін сандар ( Z ) жиыны 5) Математикаға координаттар әдісін енгізген француз математигі: А) Евклид В) Рене Декарт С) Архимед Д) Лобачевский Е) Фалес 2С В А А В

6 слайд

1) Тікбұрышты үшбұрыштың ауданы оның ... А) табаны мен сәйкес биіктігі көбейтіндісінің жартысына тең; В) табандарының жарты қосындысы мен биіктігінің көбейтіндісіне тең; С) катеттері көбейтіндісінің жартысына тең; Д) іргелес жатқан екі қабырғасының көбейтіндісіне тең; Е) табаны мен биіктігінің көбейтіндісіне тең; 2) Пифагор өрнектейтін теорема ... А) тікбұрышты үшбұрыштың бұрыштарын ; В) тікбұрышты үшбұрыштың қабырғаларының арасындағы қатынасты ; С) тікбұрышты үшбұрыштың гипотенузасын ; Д) кез – келген үшбұрыштың қабырғаларын; Е) тең бүйірлі үшбұрыштың бұрыштарын . 3) y = ax + b функциясының графигі А) түзу В) шеңбер С) парабола Д) гипербола Е) кубтық парабола 4) y = ax + bx + c квадраттық функцияның анықталу облысы А) барлық нақты сандар ( R ) жиыны Д) натурал сандар жиыны В) рационал сандар ( Q ) жиыны Е) иррационал сандар жиыны С) бүтін сандар ( Z ) жиыны 5) Математикаға координаттар әдісін енгізген француз математигі: А) Евклид В) Рене Декарт С) Архимед Д) Лобачевский Е) Фалес 2С В А А В

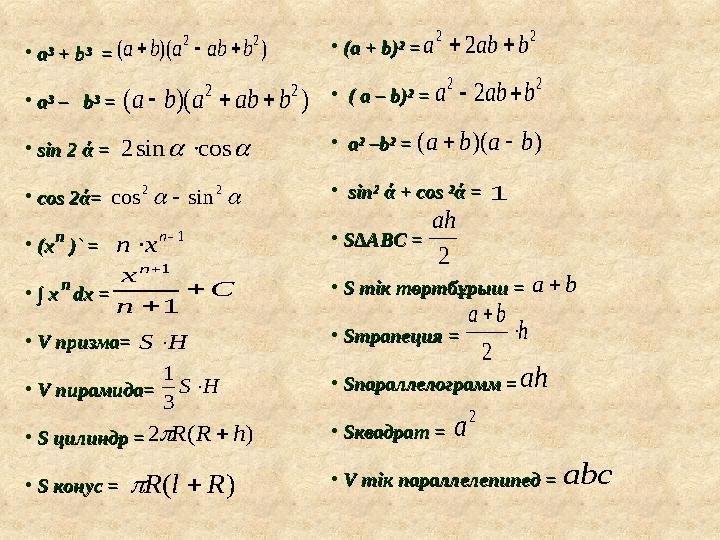
7 слайд
• a³ + b³ = a³ + b³ = • a³ – b³ = a³ – b³ = • sin sin 2 ά2 ά = = • cos cos 2ά2ά == • (x(x )` =)` = • ∫∫ x x dx = dx = • V V призмапризма == • VV пирамида пирамида == • SS цилиндр цилиндр = = • SS конус конус = =nn nn) )( ( 2 2 b ab a b a    ) )( ( 2 2 b ab a b a      cos sin 2    2 2 sin cos  1  n x n C n x n    1 1 H S  H S  3 1 ) ( 2 h R R   ) ( R l R   • (a + b)²(a + b)² == • ( a – b)²( a – b)² = = • a² –b² =a² –b² = • sin² sin² ά ά + cos ²+ cos ² ά ά == • S∆ABC =S∆ABC = • SS тік төртбұрыш тік төртбұрыш == • SS трапеция трапеция == • SS параллелограмм параллелограмм == • SS квадрат квадрат == • V V тік параллелепипед тік параллелепипед == 2 2 2 b ab a   2 2 2 b ab a   ) )( ( b a b a   1 2 ah h b a   2 ah 2 a b a  abc

7 слайд

• a³ + b³ = a³ + b³ = • a³ – b³ = a³ – b³ = • sin sin 2 ά2 ά = = • cos cos 2ά2ά == • (x(x )` =)` = • ∫∫ x x dx = dx = • V V призмапризма == • VV пирамида пирамида == • SS цилиндр цилиндр = = • SS конус конус = =nn nn) )( ( 2 2 b ab a b a    ) )( ( 2 2 b ab a b a      cos sin 2    2 2 sin cos  1  n x n C n x n    1 1 H S  H S  3 1 ) ( 2 h R R   ) ( R l R   • (a + b)²(a + b)² == • ( a – b)²( a – b)² = = • a² –b² =a² –b² = • sin² sin² ά ά + cos ²+ cos ² ά ά == • S∆ABC =S∆ABC = • SS тік төртбұрыш тік төртбұрыш == • SS трапеция трапеция == • SS параллелограмм параллелограмм == • SS квадрат квадрат == • V V тік параллелепипед тік параллелепипед == 2 2 2 b ab a   2 2 2 b ab a   ) )( ( b a b a   1 2 ah h b a   2 ah 2 a b a  abc

8 слайд
1.Теңдеуді шешіңіз: 2 y +8 y³ = 0 А) – 2; 0; 2 В) 0; 2 С) – 2; 2 Д) 0 Е) 4 1. Есептеңіз: (1/3 + 0,75) : (2/3 + 5/12) A ) 2 B ) 4 C ) 1 D ) -1 E ) 5 2 . 120 – дан 30 % табыңыз А) 47 В) 36 С) 59 Д) 24 Е) 662. Функцияның туындысын табыңыз:2 2 2 x 2 6x - E) x 2 Ä) 3- Ñ) x 2 - B) 3x A) 3 2 ) (    x x x f 5

8 слайд

1.Теңдеуді шешіңіз: 2 y +8 y³ = 0 А) – 2; 0; 2 В) 0; 2 С) – 2; 2 Д) 0 Е) 4 1. Есептеңіз: (1/3 + 0,75) : (2/3 + 5/12) A ) 2 B ) 4 C ) 1 D ) -1 E ) 5 2 . 120 – дан 30 % табыңыз А) 47 В) 36 С) 59 Д) 24 Е) 662. Функцияның туындысын табыңыз:2 2 2 x 2 6x - E) x 2 Ä) 3- Ñ) x 2 - B) 3x A) 3 2 ) (    x x x f 5

9 слайд
3.Радиусы 10 м болатын шеңбер ұзындығын табыңыз А) 40 π м В) 35 π м С) 20 π м Д) 30 π м Е)10 π м 3. Х – ті табыңыз: (5х + 2) / 9 = 1 / 2 А) 12 В) 15 С) – 0,3 Д) 0,2 Е) 0,5 4.Түбірді табыңыз:c b 0,15a E) b 5a Ä) 0,3c b 5a C) c b a B) 0,3c b 5a A) 0,027c b 125a 3 2 3 2 6 2 2 2 3 2 3 3 9 6 4.Арифметикалық прогрессияның алтыншы мүшесін табыңыз 3 E) 5 Ä) 4 C) 6 B) 8 A) 3 21 n a n   

9 слайд

3.Радиусы 10 м болатын шеңбер ұзындығын табыңыз А) 40 π м В) 35 π м С) 20 π м Д) 30 π м Е)10 π м 3. Х – ті табыңыз: (5х + 2) / 9 = 1 / 2 А) 12 В) 15 С) – 0,3 Д) 0,2 Е) 0,5 4.Түбірді табыңыз:c b 0,15a E) b 5a Ä) 0,3c b 5a C) c b a B) 0,3c b 5a A) 0,027c b 125a 3 2 3 2 6 2 2 2 3 2 3 3 9 6 4.Арифметикалық прогрессияның алтыншы мүшесін табыңыз 3 E) 5 Ä) 4 C) 6 B) 8 A) 3 21 n a n   

10 слайд
5.Үшбұрышты тік призманың табан қабырғалары 10см, 17см, 21 см, ал биіктігі 18 см.Призманың көлемін табыңыз: 5.Үшбұрыштың екі сыртқы бұрышы 100 және 150. Үшбұрыштың үшінші сыртқы бұрышын табыңыз: А) 120 В) 110 С) 130 Д) 105 Е) 903 3 3 3 3 1742ñì E) 1217ñì Ä) 1625ñì C) 1410ñì B) 1512ñì A)

10 слайд

5.Үшбұрышты тік призманың табан қабырғалары 10см, 17см, 21 см, ал биіктігі 18 см.Призманың көлемін табыңыз: 5.Үшбұрыштың екі сыртқы бұрышы 100 және 150. Үшбұрыштың үшінші сыртқы бұрышын табыңыз: А) 120 В) 110 С) 130 Д) 105 Е) 903 3 3 3 3 1742ñì E) 1217ñì Ä) 1625ñì C) 1410ñì B) 1512ñì A)

11 слайд
Жоба қорғау 1.Пирамида табаны – қабырғалары 6см және 8см болатын тік төртбұрыш. Пирамида биіктігі 12см. Барлық бүйір қырлары тең. Бүйір қырларын табыңыз. 1. Тік бұрышты үшбұрыштың гипотенузасы 41 см-ге, ал оның ауданы 180 см – ге тең. Осы үшбұрыштың катеттерін табыңыз. 2

11 слайд

Жоба қорғау 1.Пирамида табаны – қабырғалары 6см және 8см болатын тік төртбұрыш. Пирамида биіктігі 12см. Барлық бүйір қырлары тең. Бүйір қырларын табыңыз. 1. Тік бұрышты үшбұрыштың гипотенузасы 41 см-ге, ал оның ауданы 180 см – ге тең. Осы үшбұрыштың катеттерін табыңыз. 2

12 слайд