Материалдар / Теңдеулерді итерация әдісімен шешу

Теңдеулерді итерация әдісімен шешу

Материал туралы қысқаша түсінік

Теңдеулерді итерация әдісімен шешу 12 сынып оқушыларының статистика бөлімі бойынша білімдерін шыңдауға көмекші слайд топтамасы

Асет Насихат

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

15 Наурыз 2022

417

0 рет жүктелген

Алгебра Презентация 12 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 31

Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз!

Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі.

Оқу-ағарту министірлігінің ресми жауабы

Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!

Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз!

Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!

Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз!

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Сандық әдістер Теңдеулерді итерация әдісімен шешу 12.2.2.4 теңдеулерді шешуде қарапайым итерация және жартылай бөлу әдістерін қолдану

1 слайд

Сандық әдістер Теңдеулерді итерация әдісімен шешу 12.2.2.4 теңдеулерді шешуде қарапайым итерация және жартылай бөлу әдістерін қолдану

2 слайд
«Миға шабуыл» Есеп. Келесі теңдеулердің қайсысын алгебралық әдіспен шешуге болады, ал қайсыларын болмайды? Әр теңдеу үшін нақты немесе жуық шешімін табыңыз. 1) 2) 3) 4) 5)

2 слайд

«Миға шабуыл» Есеп. Келесі теңдеулердің қайсысын алгебралық әдіспен шешуге болады, ал қайсыларын болмайды? Әр теңдеу үшін нақты немесе жуық шешімін табыңыз. 1) 2) 3) 4) 5)

3 слайд
Сызықты емес теңдеулерді екіге бөлуге болады - алгебралық және трансценденттік. Алгебралық теңдеулер деп тек алгебралық функциялардан тұратын теңдеулерді айтады (бүтін, рационал, иррационал). Көпмүше негізінен бүтін алгебралық функция болып табылады. Басқа функциялардан құралған (тригонометриялық, көрсеткіштік, логарифмдік және басқалар) теңдеулерді трансценденттік теңдеулер деп атайды. Сызықты емес теңдеулерді шешу әдістері екі топқа бөлінеді: 1. Нақты әдістер ; 2. Итерациялық әдістер . Нақты әдістерде түбірді қандай да бір шекті қатынас (формула) түрінде жазуға болады. Мектептің алгебра курсынан тригонометриялық, логарифмдік, көрсеткіштік, сондай-ақ қарапайым алгебралық теңдеулерді шешу әдістері белгілі. Көптеген теңдеулер мен теңдеулер жүйелердің аналитикалық шешімі болмайтыны белгілі. Бірінші кезекте бұл көптеген трансценденттік теңдеулерге қатысты. Төртінші дәрежелі теңдеулерден жоғары алгебралық кезкелген теңдеулерді шешу формуласын құру болмайтыны дәлелденген. Сонымен қатар, кейбір жағдайларда теңдеуде тек шамамен белгілі коэффициенттер бар, демек, теңдеудің түбірін дәл анықтау туралы есептің өзі мағынаны жоғалтады. Оларды шешу үшін берілген дәлдік дәрежесі бар итерациялық әдістер қолданылады.

3 слайд

Сызықты емес теңдеулерді екіге бөлуге болады - алгебралық және трансценденттік. Алгебралық теңдеулер деп тек алгебралық функциялардан тұратын теңдеулерді айтады (бүтін, рационал, иррационал). Көпмүше негізінен бүтін алгебралық функция болып табылады. Басқа функциялардан құралған (тригонометриялық, көрсеткіштік, логарифмдік және басқалар) теңдеулерді трансценденттік теңдеулер деп атайды. Сызықты емес теңдеулерді шешу әдістері екі топқа бөлінеді: 1. Нақты әдістер ; 2. Итерациялық әдістер . Нақты әдістерде түбірді қандай да бір шекті қатынас (формула) түрінде жазуға болады. Мектептің алгебра курсынан тригонометриялық, логарифмдік, көрсеткіштік, сондай-ақ қарапайым алгебралық теңдеулерді шешу әдістері белгілі. Көптеген теңдеулер мен теңдеулер жүйелердің аналитикалық шешімі болмайтыны белгілі. Бірінші кезекте бұл көптеген трансценденттік теңдеулерге қатысты. Төртінші дәрежелі теңдеулерден жоғары алгебралық кезкелген теңдеулерді шешу формуласын құру болмайтыны дәлелденген. Сонымен қатар, кейбір жағдайларда теңдеуде тек шамамен белгілі коэффициенттер бар, демек, теңдеудің түбірін дәл анықтау туралы есептің өзі мағынаны жоғалтады. Оларды шешу үшін берілген дәлдік дәрежесі бар итерациялық әдістер қолданылады.

4 слайд

5 слайд
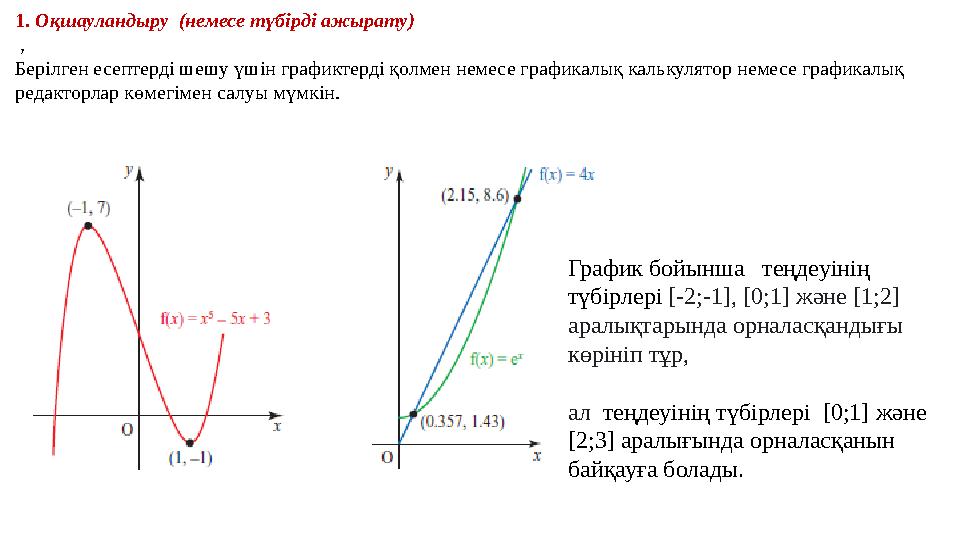
1. Оқшауландыру (немесе түбірді ажырату) , Берілген есептерді шешу үшін графиктерді қолмен немесе графикалық калькулятор немесе графикалық редакторлар көмегімен салуы мүмкін. График бойынша теңдеуінің түбірлері [-2;-1], [0;1] және [1;2] аралықтарында орналасқандығы көрініп тұр , ал теңдеуінің түбірлері [0;1] және [2;3] аралығында орналасқанын байқауға болады .

5 слайд

1. Оқшауландыру (немесе түбірді ажырату) , Берілген есептерді шешу үшін графиктерді қолмен немесе графикалық калькулятор немесе графикалық редакторлар көмегімен салуы мүмкін. График бойынша теңдеуінің түбірлері [-2;-1], [0;1] және [1;2] аралықтарында орналасқандығы көрініп тұр , ал теңдеуінің түбірлері [0;1] және [2;3] аралығында орналасқанын байқауға болады .

6 слайд
Түбірдің оқшауландырылуы [a, b] кесіндісінде жалғыз тек қана жалғыз түбірін анықтаудан тұрады. Түбірді оқшаулаудың әмбебап (универсал) алгоритмі жоқ. Кейбір жағдайларда оқшаулау кесіндісі жеке ойлардан табылуы мүмкін. Түбірді оқшаулау кейде графикті салу немесе функциясының мәндер кестесін құру арқылы ыңғайлы. Кесіндіде түбірдің бар болуына [а, b] кесіндінің ұшындағы функция таңбаларының айырмашылықтарын көрсетеді. Бұған математикалық талдаудың келесі теоремасы негіз болады. Теорема . Егер f функциясы [a; b] кесіндісінде үздіксіз болса және оның ұшында әр түрлі таңбалы мәндерді қабылдаса, сондықтан , онда [а; b] кесіндісінде теңдеудің кем дегенде бір түбірі бар.

6 слайд

Түбірдің оқшауландырылуы [a, b] кесіндісінде жалғыз тек қана жалғыз түбірін анықтаудан тұрады. Түбірді оқшаулаудың әмбебап (универсал) алгоритмі жоқ. Кейбір жағдайларда оқшаулау кесіндісі жеке ойлардан табылуы мүмкін. Түбірді оқшаулау кейде графикті салу немесе функциясының мәндер кестесін құру арқылы ыңғайлы. Кесіндіде түбірдің бар болуына [а, b] кесіндінің ұшындағы функция таңбаларының айырмашылықтарын көрсетеді. Бұған математикалық талдаудың келесі теоремасы негіз болады. Теорема . Егер f функциясы [a; b] кесіндісінде үздіксіз болса және оның ұшында әр түрлі таңбалы мәндерді қабылдаса, сондықтан , онда [а; b] кесіндісінде теңдеудің кем дегенде бір түбірі бар.

7 слайд
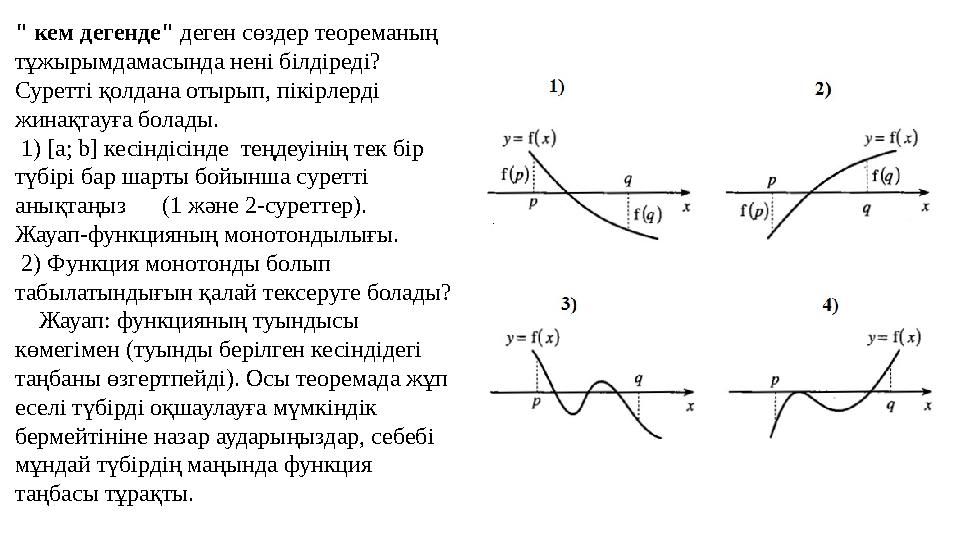
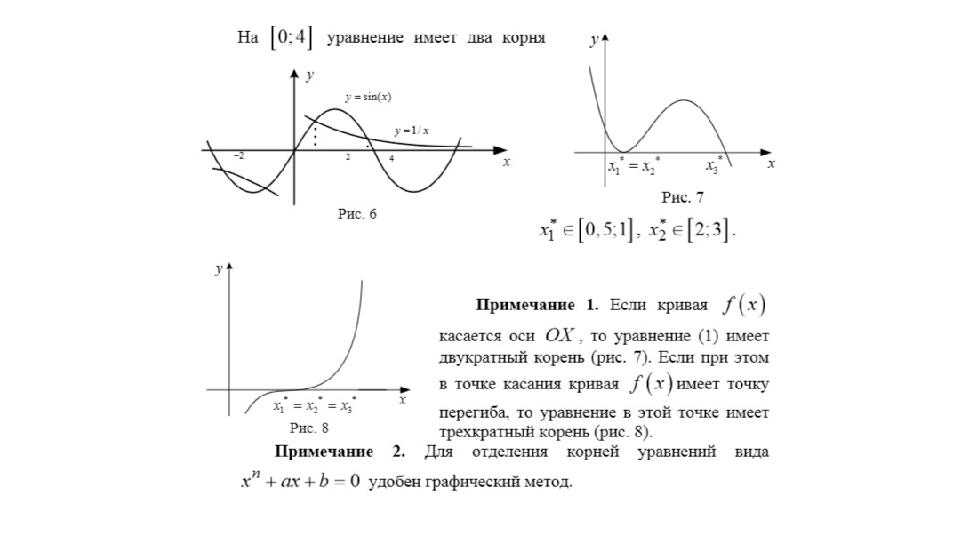
" кем дегенде" деген сөздер теореманың тұжырымдамасында нені білдіреді? Суретті қолдана отырып, пікірлерді жинақтауға болады. 1) [a; b] кесіндісінде теңдеуінің тек бір түбірі бар шарты бойынша суретті анықтаңыз (1 және 2-суреттер). Жауап-функцияның монотондылығы. 2) Функция монотонды болып табылатындығын қалай тексеруге болады? Жауап: функцияның туындысы көмегімен (туынды берілген кесіндідегі таңбаны өзгертпейді). Осы теоремада жұп еселі түбірді оқшаулауға мүмкіндік бермейтініне назар аударыңыздар, себебі мұндай түбірдің маңында функция таңбасы тұрақты.

7 слайд

" кем дегенде" деген сөздер теореманың тұжырымдамасында нені білдіреді? Суретті қолдана отырып, пікірлерді жинақтауға болады. 1) [a; b] кесіндісінде теңдеуінің тек бір түбірі бар шарты бойынша суретті анықтаңыз (1 және 2-суреттер). Жауап-функцияның монотондылығы. 2) Функция монотонды болып табылатындығын қалай тексеруге болады? Жауап: функцияның туындысы көмегімен (туынды берілген кесіндідегі таңбаны өзгертпейді). Осы теоремада жұп еселі түбірді оқшаулауға мүмкіндік бермейтініне назар аударыңыздар, себебі мұндай түбірдің маңында функция таңбасы тұрақты.

8 слайд
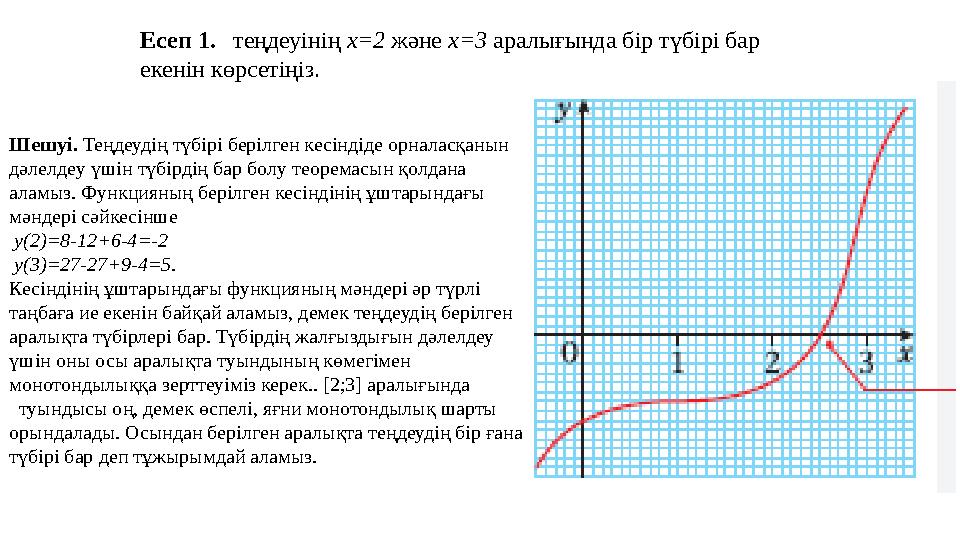
Есеп 1. теңдеуінің x=2 және x=3 аралығында бір түбірі бар екенін көрсетіңіз. Шешуі. Теңдеудің түбірі берілген кесіндіде орналасқанын дәлелдеу үшін түбірдің бар болу теоремасын қолдана аламыз. Функцияның берілген кесіндінің ұштарындағы мәндері сәйкесінше y (2)=8-12+6-4=-2 y ( 3)=27-27+9-4=5 . Кесіндінің ұштарындағы функцияның мәндері әр түрлі таңбаға ие екенін байқай аламыз, демек теңдеудің берілген аралықта түбірлері бар. Түбірдің жалғыздығын дәлелдеу үшін оны осы аралықта туындының көмегімен монотондылыққа зерттеуіміз керек.. [2;3] аралығында туындысы оң, демек өспелі, яғни монотондылық шарты орындалады. Осындан берілген аралықта теңдеудің бір ғана түбірі бар деп тұжырымдай аламыз.

8 слайд

Есеп 1. теңдеуінің x=2 және x=3 аралығында бір түбірі бар екенін көрсетіңіз. Шешуі. Теңдеудің түбірі берілген кесіндіде орналасқанын дәлелдеу үшін түбірдің бар болу теоремасын қолдана аламыз. Функцияның берілген кесіндінің ұштарындағы мәндері сәйкесінше y (2)=8-12+6-4=-2 y ( 3)=27-27+9-4=5 . Кесіндінің ұштарындағы функцияның мәндері әр түрлі таңбаға ие екенін байқай аламыз, демек теңдеудің берілген аралықта түбірлері бар. Түбірдің жалғыздығын дәлелдеу үшін оны осы аралықта туындының көмегімен монотондылыққа зерттеуіміз керек.. [2;3] аралығында туындысы оң, демек өспелі, яғни монотондылық шарты орындалады. Осындан берілген аралықта теңдеудің бір ғана түбірі бар деп тұжырымдай аламыз.

9 слайд
3. функциясы берілген. теңдеуінің түбірі болатынын көрсетіңіз, мұндағы [1;2] аралығында орналасқан. 4. функциясы берілген. a. Кестені толтырыңыз b . теңдеуінің теріс түбірі α және α+1 аралығында орналасқаны белгілі , мұндағы α – бүтін сан . -ның мәнін табыңыз .2. аралығында жататын түбірлерін график арқылы оқшаулаңыз.

9 слайд

3. функциясы берілген. теңдеуінің түбірі болатынын көрсетіңіз, мұндағы [1;2] аралығында орналасқан. 4. функциясы берілген. a. Кестені толтырыңыз b . теңдеуінің теріс түбірі α және α+1 аралығында орналасқаны белгілі , мұндағы α – бүтін сан . -ның мәнін табыңыз .2. аралығында жататын түбірлерін график арқылы оқшаулаңыз.

10 слайд
Инженерлік практикада жуық түбірлерді анықтаудың графикалық тәсілі кең таралған. Теңдеудің нақты түбірі – бұл абсцисса осімен f(x) функциясының графигінің қиылысу нүктелері екенін назарға ала отырып, f(x) функциясының графигін құру және f (x) функциясының Ох осімен қиылысу нүктелерін белгілеу жеткілікті немесе Ох осінде бір түбірінен тұратын кесінді белгілеу керек. Көбінесе f(x)=0 теңдеуін оған тең шамалас теңдеуімен алмастырып графиктерді салу ықшамдалады. f 1 ( x ) және f 2 ( x ) функциялары f ( x ) функциясына қарағанда қарапайым. у = f 1 ( x ) және у = f 2 ( x ) функцияларының графиктерін салып, ізделінді түбірлерді осы графиктердің қиылысу нүктелерінің абсциссалары ретінде анықтаймыз. у = f 1 (x) және у = f 2 (x) функцияларды таңдау әр түрлі болуы мүмкін екенін көрсету үшін келесі мысалдарды қарастырайық.

10 слайд

Инженерлік практикада жуық түбірлерді анықтаудың графикалық тәсілі кең таралған. Теңдеудің нақты түбірі – бұл абсцисса осімен f(x) функциясының графигінің қиылысу нүктелері екенін назарға ала отырып, f(x) функциясының графигін құру және f (x) функциясының Ох осімен қиылысу нүктелерін белгілеу жеткілікті немесе Ох осінде бір түбірінен тұратын кесінді белгілеу керек. Көбінесе f(x)=0 теңдеуін оған тең шамалас теңдеуімен алмастырып графиктерді салу ықшамдалады. f 1 ( x ) және f 2 ( x ) функциялары f ( x ) функциясына қарағанда қарапайым. у = f 1 ( x ) және у = f 2 ( x ) функцияларының графиктерін салып, ізделінді түбірлерді осы графиктердің қиылысу нүктелерінің абсциссалары ретінде анықтаймыз. у = f 1 (x) және у = f 2 (x) функцияларды таңдау әр түрлі болуы мүмкін екенін көрсету үшін келесі мысалдарды қарастырайық.

11 слайд
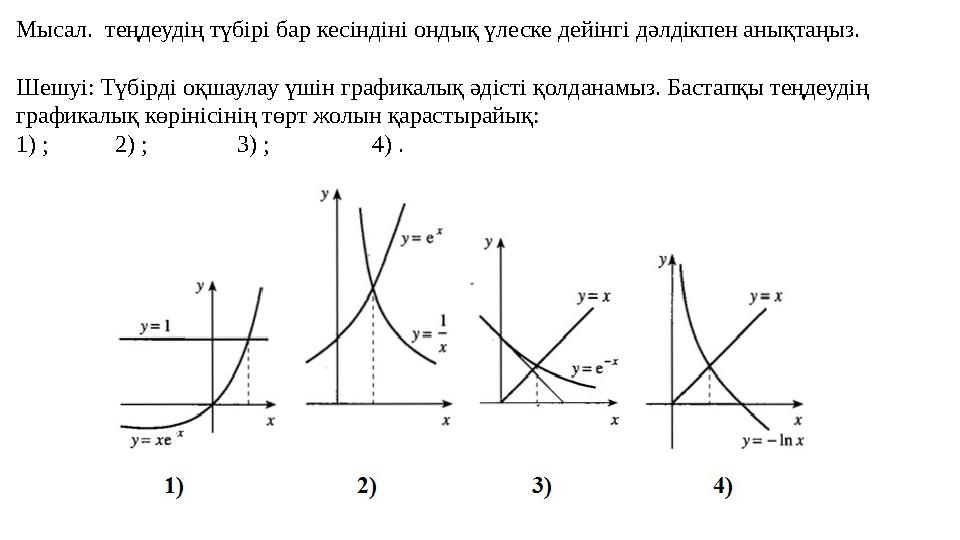
Мысал. теңдеудің түбірі бар кесіндіні ондық үлеске дейінгі дәлдікпен анықтаңыз. Шешуі: Түбірді оқшаулау үшін графикалық әдісті қолданамыз. Бастапқы теңдеудің графикалық көрінісінің төрт жолын қарастырайық: 1) ; 2) ; 3) ; 4) .

11 слайд

Мысал. теңдеудің түбірі бар кесіндіні ондық үлеске дейінгі дәлдікпен анықтаңыз. Шешуі: Түбірді оқшаулау үшін графикалық әдісті қолданамыз. Бастапқы теңдеудің графикалық көрінісінің төрт жолын қарастырайық: 1) ; 2) ; 3) ; 4) .

12 слайд
Төрт суреттің барлығында теңдеудің бір түбірі бар екені көрініп тұр, дегенмен үшінші суретте ақпарат көбірек. функциясының нүктесіндегі жанамасының бұрыштық коэффициенті тең, жанама мен теңдеуінің қиылысу нүктесінің координатасы . Яғни теңдеудің түбірі 0,5- тен шамалы үлкен. Түбірі бар кесіндіні анықтау үшін бастапқы теңдеуді түрінде көрсетеміз және болжамды кесіндінің ұшында функцияның қандай таңбаларды қабылдайтынын анықтаймыз: Тең шамалас нұсқаларды қарастырайық: 1) ; 2) ; 3) ; 4) . Калькулятор арқылы есептеу үшін төртінші нұсқа ыңғайлы, өйткені орындалатын әрекеттер аз. қолдана отырып, және аламыз. (сондай ақ теңдеуі) теңдеуінің түбірлері кесіндісіне тиесілі. бұл кесіндіде функциясы монотонды болғандықтан және осы кесіндінің ұшындағы әр түрлі таңбалы мәндерді қабылдайды.

12 слайд

Төрт суреттің барлығында теңдеудің бір түбірі бар екені көрініп тұр, дегенмен үшінші суретте ақпарат көбірек. функциясының нүктесіндегі жанамасының бұрыштық коэффициенті тең, жанама мен теңдеуінің қиылысу нүктесінің координатасы . Яғни теңдеудің түбірі 0,5- тен шамалы үлкен. Түбірі бар кесіндіні анықтау үшін бастапқы теңдеуді түрінде көрсетеміз және болжамды кесіндінің ұшында функцияның қандай таңбаларды қабылдайтынын анықтаймыз: Тең шамалас нұсқаларды қарастырайық: 1) ; 2) ; 3) ; 4) . Калькулятор арқылы есептеу үшін төртінші нұсқа ыңғайлы, өйткені орындалатын әрекеттер аз. қолдана отырып, және аламыз. (сондай ақ теңдеуі) теңдеуінің түбірлері кесіндісіне тиесілі. бұл кесіндіде функциясы монотонды болғандықтан және осы кесіндінің ұшындағы әр түрлі таңбалы мәндерді қабылдайды.

13 слайд
Жуық түбірлерді нақтылау Теңдеу түбірлерінің жуық мәнін табудың түрлі әдістері бар. Олардың екеуін қарастырайық: жартысын бөлу әдісі және қарапайым итерация әдісі. 1. Жартысын бөлу әдісі. Кесіндіні екіге бөлу әдісі сызықты емес теңдеуді шешудің ең қарапайым және сенімді тәсілі болып табылады. Алдынғы талдаудан теңдеудің түбірі кесіндіде екені белгілі болсын, яғни x* ∈ , сондықтан f(x*) = 0. f (x) функциясы кесіндісінде үздіксіз болсын және ұштарында әр түрлі таңбалы мәндерді қабылдасын, яғни . кесіндіні қақ екіге бөлеміз. нүктесін аламыз. Осы нүктедегі функцияның мәнін есептейік: . Егер болса, онда -ізделінді түбір, және есеп шешілді. Егер болса, онда - белгілі бір таңбалы сан: және . Сонда немесе кесіндінің ұштарында, немесе кесіндінің ұштарында f(x) функциясының мәндері әртүрлі таңбаларға ие болады. Мұндай кесіндіні деп белгілейміз. Әрине x* ∈ екені анық және кесіндісінің ұзындығы кесіндісінің ұзындығына қарағанда екі есе аз. кесіндісімен де ұқсас әрекет жасаймыз. Нәтижесінде не түбір, немесе жаңа кесінді аламыз және т.с.с. теңсіздік орындалған кезде берілген дәлдікпен жуықтап ε есептеулер аяқталады

13 слайд

Жуық түбірлерді нақтылау Теңдеу түбірлерінің жуық мәнін табудың түрлі әдістері бар. Олардың екеуін қарастырайық: жартысын бөлу әдісі және қарапайым итерация әдісі. 1. Жартысын бөлу әдісі. Кесіндіні екіге бөлу әдісі сызықты емес теңдеуді шешудің ең қарапайым және сенімді тәсілі болып табылады. Алдынғы талдаудан теңдеудің түбірі кесіндіде екені белгілі болсын, яғни x* ∈ , сондықтан f(x*) = 0. f (x) функциясы кесіндісінде үздіксіз болсын және ұштарында әр түрлі таңбалы мәндерді қабылдасын, яғни . кесіндіні қақ екіге бөлеміз. нүктесін аламыз. Осы нүктедегі функцияның мәнін есептейік: . Егер болса, онда -ізделінді түбір, және есеп шешілді. Егер болса, онда - белгілі бір таңбалы сан: және . Сонда немесе кесіндінің ұштарында, немесе кесіндінің ұштарында f(x) функциясының мәндері әртүрлі таңбаларға ие болады. Мұндай кесіндіні деп белгілейміз. Әрине x* ∈ екені анық және кесіндісінің ұзындығы кесіндісінің ұзындығына қарағанда екі есе аз. кесіндісімен де ұқсас әрекет жасаймыз. Нәтижесінде не түбір, немесе жаңа кесінді аламыз және т.с.с. теңсіздік орындалған кезде берілген дәлдікпен жуықтап ε есептеулер аяқталады

14 слайд

15 слайд

16 слайд
2. Қарапайым интерация әдісі теңдеуді оған баламалы теңдеуімен алмастырылуы болсын. Қандайда бастапқы жуықтауды таңдаймыз. болғандағы функциясының мәнін есептейміз және болғандағы нақты мәнін анықтаймыз. Енді -ді теңдеуіне қойып, жаңа жуықтауды аламыз және т. с.с. Бұл процесті шексіз жалғастыра отырып, түбірге жақындаудың тізбегін аламыз: . формуласы қарапайым итерация әдісінің есептік формуласы болып табылады. Егер тізбегі n→ ∞ болса, яғни бар және функциясы үздіксіз, теңдігінің шегіне өте отырып және ескере отырып, аламыз: . Сонымен , демек теңдеуінің түбірі - теңдеуін түрлі тәсілдермен оған баламалы теңдеуімен алмастыруға болады. Бұл ретте әрдайым түбірге жақындау тізбегінің шегі бола бермейді. Егер алынған тізбектің шегі болмаса, онда басқа тізбегінің шегін таба алатындай түріндегі түрлендіруді алу керек. Алынған шек теңдеуінің түбірі болып табылады, яғни теңдеудің де.

16 слайд

2. Қарапайым интерация әдісі теңдеуді оған баламалы теңдеуімен алмастырылуы болсын. Қандайда бастапқы жуықтауды таңдаймыз. болғандағы функциясының мәнін есептейміз және болғандағы нақты мәнін анықтаймыз. Енді -ді теңдеуіне қойып, жаңа жуықтауды аламыз және т. с.с. Бұл процесті шексіз жалғастыра отырып, түбірге жақындаудың тізбегін аламыз: . формуласы қарапайым итерация әдісінің есептік формуласы болып табылады. Егер тізбегі n→ ∞ болса, яғни бар және функциясы үздіксіз, теңдігінің шегіне өте отырып және ескере отырып, аламыз: . Сонымен , демек теңдеуінің түбірі - теңдеуін түрлі тәсілдермен оған баламалы теңдеуімен алмастыруға болады. Бұл ретте әрдайым түбірге жақындау тізбегінің шегі бола бермейді. Егер алынған тізбектің шегі болмаса, онда басқа тізбегінің шегін таба алатындай түріндегі түрлендіруді алу керек. Алынған шек теңдеуінің түбірі болып табылады, яғни теңдеудің де.

17 слайд

18 слайд
Аралқты

18 слайд

Аралқты

19 слайд
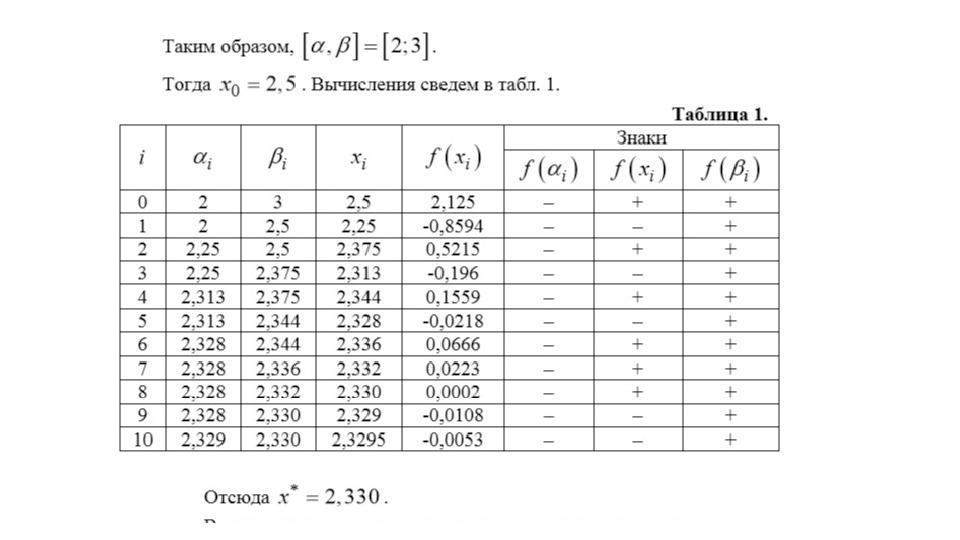
Мысал. теңдеуінің түбірін табыңыз. Шешуі: Өрнекті түріне келтіреміз. Графикалық әдісті пайдалана отырып, бұл теңдеудің бір түбірі бар екенін көруге болады. функциясы функциясына қарағанда жылдамырақ өскендіктен басқа қиылысу нүктелері жоқ. функциясы кесіндісінде үздіксіз және болғандықтан, теңдеуінің түбірі кесіндісіне тиісті. Түбірді анықтаудың екі әдісін қарастырайық. 1 әдіс : жартысын бөлу әдісі. Теңдеудің түбірін дейінгі дәлдікпен табамыз. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. және болғандықтан теңдеудің түбірі шамамен тең.

19 слайд

Мысал. теңдеуінің түбірін табыңыз. Шешуі: Өрнекті түріне келтіреміз. Графикалық әдісті пайдалана отырып, бұл теңдеудің бір түбірі бар екенін көруге болады. функциясы функциясына қарағанда жылдамырақ өскендіктен басқа қиылысу нүктелері жоқ. функциясы кесіндісінде үздіксіз және болғандықтан, теңдеуінің түбірі кесіндісіне тиісті. Түбірді анықтаудың екі әдісін қарастырайық. 1 әдіс : жартысын бөлу әдісі. Теңдеудің түбірін дейінгі дәлдікпен табамыз. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. , яғни түбір аралығына тиісті. және болғандықтан теңдеудің түбірі шамамен тең.

20 слайд

21 слайд

22 слайд

23 слайд

24 слайд

25 слайд

26 слайд

27 слайд

28 слайд

29 слайд

30 слайд