
4.1. Тақырып №2
4.2. Мақсаты:
Оқушылар функцияның қасиеттерін қарастырады. Есептерді шығару барысында функцияның қасиеттерін тани біледі
4.3. Дәрістің тезисі:
1. Сендер қандай функциялармен таныссыңдар?
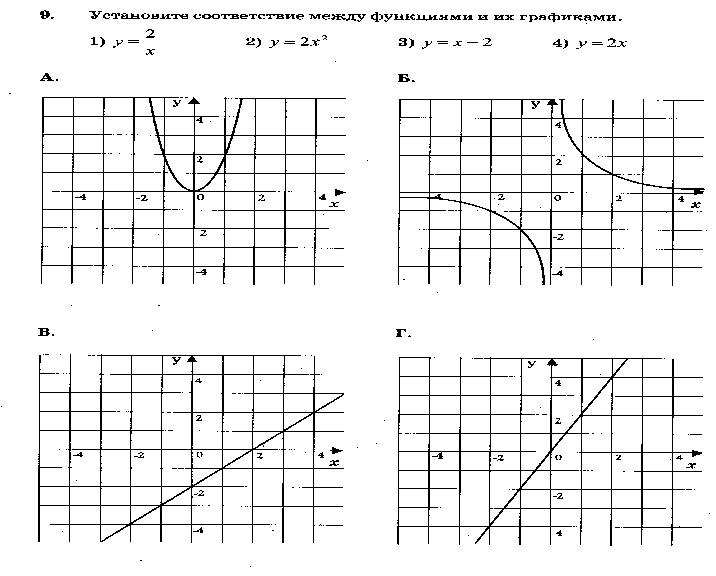
2. Функциялар мен олардың графиктерінің арасындағы сәйкестікті орнатыңдар?
https://daryn.online/lesson/7202-funktsyya-qasyetteri (сілтемесі арқылы өтіп, қосымша мәлімет алып, тапсырмаларды орындауыңызға болады)
Практикалық жұмыстар.
Оқушылар презентациямен жұмыс жасайды. Тапсырмаларды оқушылар жекелей орындайды, соңынан сыныппен тексереді.
А) функцияның анықталу және мәндер облысын анықтау.
Берілген функциялар үшін анықталу және мәндер облысын атаңдар.
![]()
![]()
Б) жұп/тақтылығы
Берілген уақытта барынша көп функциялардың жұп/тақтылығын анықтап үлгеру.
(Бағалау: Көп фунцияларды анықтаған және қате жібермеген оқушыларды атау қажет.)
В) функцияның нөлдері
Оқушылармен мысалдар арқылы функцияның нөлдері деген ұғымды талдау. Өз беттерінше функцияның нөлдерін анықтау.


(Тапсырманы орындап болған соң, өзара тексеру өткізу. Бағалау: оқушылар бірін-бірі бағалайды.)
C) Функцияның өсу/кемуі
Оқушылармен функцияның өсу және кемуі туралы анықтамаларды қарастыру. Берілген функциялардың жұп/тақтылығын жұппен талдау және оны дәлелдеу.
D) функциялардың периодтылығы
Оқушыларды функцияның периодтылығы мен ең кіші периоды ұғымымен таныстыру.
Сабақта алған білімдерін тексеру үшін, өз беттерінше орындауға тапсырмалар:
Берілген уақытта нұсқалар бойынша тапсырмаларды орындау.
Слайдтағы жауабы бойынша өзін-өзі тексеру.
Қосымша(кейбір оқушылар үшін):
https://itest.kz/kz/test/365658838 сілтемесі бойынша математикалық сауаттылыққа тест тапсырмаларын орындайды.
Мысалы: х² +5х+6 =0 теңдеуінің түбірлері -2 және-3 ; тексерейік х1+х2=-5; х1*х2=6;
Квадрат теңдеуді шешу тәсілдері.
Мысалы, (1)  (лақтыру әдісі) яғни 1-ші
коэффициентті бос мүшеге көбейтеміз.
(лақтыру әдісі) яғни 1-ші
коэффициентті бос мүшеге көбейтеміз.
 түбірлерін тауып, шыққан
сандарды I коэффициентке бөлеміз.
түбірлерін тауып, шыққан
сандарды I коэффициентке бөлеміз. 
(1)Теңдеудің түбірлері


Жауабы: 
Квадрат теңдеудің коэффициенттерінің қасиетін қолдану.
Квадрат теңдеудің
коэффиценттерінің қосындысы нөлге тең болса, онда  ; болады.
; болады.
(Егер ІІ коэффициент I
коэффицент пен бос мүшенің қосындысына тең болса, онда
 теңдеуінің бірінші түбірі
-1-ге, ал екінші түбірі бос мүшені I коэффицентке бөліп “-”
таңбасымен жазуға болады.)
теңдеуінің бірінші түбірі
-1-ге, ал екінші түбірі бос мүшені I коэффицентке бөліп “-”
таңбасымен жазуға болады.)
Мысалы, 
болғандықтан  (c
(c болғандықтан
болғандықтан  болады). Осы тәсілдерді қолдану
теңдеулерді оңай, тиімді тәсілмен шапшаң шешуге мүмкіндік
береді.
болады). Осы тәсілдерді қолдану
теңдеулерді оңай, тиімді тәсілмен шапшаң шешуге мүмкіндік
береді.
Көбейткіштерге жіктеу әдісі.
Қосылғыштарды топтау әдісімен, ортақ көбейткішті жақшаның сыртына шығару арқылы немесе қысқаша көбейту формулаларын қолдану арқылы берілген теңдеудің сол жағын бірнеше көбейткіштердің көбейтіндісі түрінде жазып, оң жағын нөлге теңестіреміз. Одан соң көбейткіштердің әрқайсысын нөлге теңестіру арқылы түбірлерін анықтаймыз.
Мысалы, 1. 
 ;
;  ;
;


Мысал2.








 . Түбірі болмайды.
Жауабы: х=1
. Түбірі болмайды.
Жауабы: х=1
Жаңа айнымалы енгізу арқылы шешу.
Теңдеудегі қайталанатын өрнекті тауып, жаңа айнымалы арқылы белгілеп, неғұрлым қарапайым, оңай шешілетін теңдеуге келтіру арқылы шешуге болады.
Мысалы 1. 

 деп алсақ,
деп алсақ,



 Жауабы:
Жауабы:

Мысал 2.


теңдеуін шешу үшін



 Жауабы:
Жауабы: 
4.4. Сабақтың көрнекілігі: сызбалар, таратпа карточкалар, тест.
4.5. Әдебиеттер:
1. А.Е.Әбылқасымова, З.Ә. Жұмағұлова, Алгебра және анализ бастамалары: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 10-сыныбына арналған оқулық, Алматы: «Мектеп», 2019 ж.
2. А.Е.Әбылқасымова, З.Ә. Жұмағұлова, Алгебра және анализ бастамалары: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 11-сыныбына арналған оқулық, Алматы: «Мектеп», 2020ж.
3. В.А.Смирнов, Е.А.Тұяқов, Геометрия: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 10-сыныбына арналған оқулық, Алматы: «Мектеп», 2019 ж.
4. В.А.Смирнов, Е.А.Тұяқов, Геометрия: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 11-сыныбына арналған оқулық, Алматы: «Мектеп», 2020 ж.
5. Пак О,Ардакулы Д, Ескендирова Е, Курман Б, Анапинова Г. Алгебра және анализ бастамалары. Оқулық 1, 2 бөлім. Алматы кітап, 2019ж.
4.6. Бақылау сұрақтары:
Теңдеуді шешіңіз.
-
 9.
9.
-
 10.
10.
-
 11.
11. 
-
 12.
12. 
-
 13.
13.
-
3х*(х-1)-17=х*(1+3х)+1 14.

-
39,7х+0,5х+43,5=-36,9
-

Теңдеулерді шешіңіз. А-деңгейі:
1.а) b)
b)


2.а)
b)
3.a)
b)
егер 
4.a)
b)

5.a)

b)
6.a)
b) ;
;
7.a)
b)
8.a)
b)
9.a)
b)
10.a)
b)
B-деңгейі. Теңдеулерді шешіңіз:
1.a)
b)
2.a)
b)

3.a) 2;-4;
2;-4;
b)
4.a)
b)
5.a)
b)
C деңгейі.
1.a)31(
b)

b)
3.a)
b)
4.a)
b)
5.a)
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Функция қасиеттері.
Функция қасиеттері.
4.1. Тақырып №2
4.2. Мақсаты:
Оқушылар функцияның қасиеттерін қарастырады. Есептерді шығару барысында функцияның қасиеттерін тани біледі
4.3. Дәрістің тезисі:
1. Сендер қандай функциялармен таныссыңдар?
2. Функциялар мен олардың графиктерінің арасындағы сәйкестікті орнатыңдар?

https://daryn.online/lesson/7202-funktsyya-qasyetteri (сілтемесі арқылы өтіп, қосымша мәлімет алып, тапсырмаларды орындауыңызға болады)
Практикалық жұмыстар.
Оқушылар презентациямен жұмыс жасайды. Тапсырмаларды оқушылар жекелей орындайды, соңынан сыныппен тексереді.
А) функцияның анықталу және мәндер облысын анықтау.
Берілген функциялар үшін анықталу және мәндер облысын атаңдар.
![]()
![]()
Б) жұп/тақтылығы
Берілген уақытта барынша көп функциялардың жұп/тақтылығын анықтап үлгеру.
(Бағалау: Көп фунцияларды анықтаған және қате жібермеген оқушыларды атау қажет.)
В) функцияның нөлдері
Оқушылармен мысалдар арқылы функцияның нөлдері деген ұғымды талдау. Өз беттерінше функцияның нөлдерін анықтау.


(Тапсырманы орындап болған соң, өзара тексеру өткізу. Бағалау: оқушылар бірін-бірі бағалайды.)
C) Функцияның өсу/кемуі
Оқушылармен функцияның өсу және кемуі туралы анықтамаларды қарастыру. Берілген функциялардың жұп/тақтылығын жұппен талдау және оны дәлелдеу.
D) функциялардың периодтылығы
Оқушыларды функцияның периодтылығы мен ең кіші периоды ұғымымен таныстыру.
Сабақта алған білімдерін тексеру үшін, өз беттерінше орындауға тапсырмалар:
Берілген уақытта нұсқалар бойынша тапсырмаларды орындау.
Слайдтағы жауабы бойынша өзін-өзі тексеру.
Қосымша(кейбір оқушылар үшін):
https://itest.kz/kz/test/365658838 сілтемесі бойынша математикалық сауаттылыққа тест тапсырмаларын орындайды.
Мысалы: х² +5х+6 =0 теңдеуінің түбірлері -2 және-3 ; тексерейік х1+х2=-5; х1*х2=6;
Квадрат теңдеуді шешу тәсілдері.
Мысалы, (1)  (лақтыру әдісі) яғни 1-ші
коэффициентті бос мүшеге көбейтеміз.
(лақтыру әдісі) яғни 1-ші
коэффициентті бос мүшеге көбейтеміз.
 түбірлерін тауып, шыққан
сандарды I коэффициентке бөлеміз.
түбірлерін тауып, шыққан
сандарды I коэффициентке бөлеміз. 
(1)Теңдеудің түбірлері


Жауабы: 
Квадрат теңдеудің коэффициенттерінің қасиетін қолдану.
Квадрат теңдеудің
коэффиценттерінің қосындысы нөлге тең болса, онда  ; болады.
; болады.
(Егер ІІ коэффициент I
коэффицент пен бос мүшенің қосындысына тең болса, онда
 теңдеуінің бірінші түбірі
-1-ге, ал екінші түбірі бос мүшені I коэффицентке бөліп “-”
таңбасымен жазуға болады.)
теңдеуінің бірінші түбірі
-1-ге, ал екінші түбірі бос мүшені I коэффицентке бөліп “-”
таңбасымен жазуға болады.)
Мысалы, 
болғандықтан  (c
(c болғандықтан
болғандықтан  болады). Осы тәсілдерді қолдану
теңдеулерді оңай, тиімді тәсілмен шапшаң шешуге мүмкіндік
береді.
болады). Осы тәсілдерді қолдану
теңдеулерді оңай, тиімді тәсілмен шапшаң шешуге мүмкіндік
береді.
Көбейткіштерге жіктеу әдісі.
Қосылғыштарды топтау әдісімен, ортақ көбейткішті жақшаның сыртына шығару арқылы немесе қысқаша көбейту формулаларын қолдану арқылы берілген теңдеудің сол жағын бірнеше көбейткіштердің көбейтіндісі түрінде жазып, оң жағын нөлге теңестіреміз. Одан соң көбейткіштердің әрқайсысын нөлге теңестіру арқылы түбірлерін анықтаймыз.
Мысалы, 1. 
 ;
;  ;
;


Мысал2.








 . Түбірі болмайды.
Жауабы: х=1
. Түбірі болмайды.
Жауабы: х=1
Жаңа айнымалы енгізу арқылы шешу.
Теңдеудегі қайталанатын өрнекті тауып, жаңа айнымалы арқылы белгілеп, неғұрлым қарапайым, оңай шешілетін теңдеуге келтіру арқылы шешуге болады.
Мысалы 1. 

 деп алсақ,
деп алсақ,



 Жауабы:
Жауабы:

Мысал 2.


теңдеуін шешу үшін



 Жауабы:
Жауабы: 
4.4. Сабақтың көрнекілігі: сызбалар, таратпа карточкалар, тест.
4.5. Әдебиеттер:
1. А.Е.Әбылқасымова, З.Ә. Жұмағұлова, Алгебра және анализ бастамалары: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 10-сыныбына арналған оқулық, Алматы: «Мектеп», 2019 ж.
2. А.Е.Әбылқасымова, З.Ә. Жұмағұлова, Алгебра және анализ бастамалары: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 11-сыныбына арналған оқулық, Алматы: «Мектеп», 2020ж.
3. В.А.Смирнов, Е.А.Тұяқов, Геометрия: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 10-сыныбына арналған оқулық, Алматы: «Мектеп», 2019 ж.
4. В.А.Смирнов, Е.А.Тұяқов, Геометрия: Жалпы білім беретін мектептің қоғамдық-гуманитарлық бағытындағы 11-сыныбына арналған оқулық, Алматы: «Мектеп», 2020 ж.
5. Пак О,Ардакулы Д, Ескендирова Е, Курман Б, Анапинова Г. Алгебра және анализ бастамалары. Оқулық 1, 2 бөлім. Алматы кітап, 2019ж.
4.6. Бақылау сұрақтары:
Теңдеуді шешіңіз.
-
 9.
9.
-
 10.
10.
-
 11.
11. 
-
 12.
12. 
-
 13.
13.
-
3х*(х-1)-17=х*(1+3х)+1 14.

-
39,7х+0,5х+43,5=-36,9
-

Теңдеулерді шешіңіз. А-деңгейі:
1.а) b)
b)


2.а)
b)
3.a)
b)
егер 
4.a)
b)

5.a)

b)
6.a)
b) ;
;
7.a)
b)
8.a)
b)
9.a)
b)
10.a)
b)
B-деңгейі. Теңдеулерді шешіңіз:
1.a)
b)
2.a)
b)

3.a) 2;-4;
2;-4;
b)
4.a)
b)
5.a)
b)
C деңгейі.
1.a)31(
b)

b)
3.a)
b)
4.a)
b)
5.a)

шағым қалдыра аласыз















