
Тақырыбы: Кейбір сандардың бөлінгіштік белгілері:
Мақсаты:
1)Оқушыларды кейбір сандардың бөлінгіштік белгілері олимпиада есептерінде көптеп кездесетінін түсіндіру.
2)Оқушылардың ой-өрісін кеіейту, математикалық тілін және логикалық ойлау қабілетін дамыту.
3)Оқуға, саналы сезімге, жауапкершілікке өз бетінше еңбектенуге тәрбиелеу.
Сабақ түрі: түсіндірмелі
Көрнекілігі: АКТ, калькулятор
Сабақ барысы: 1.Ұйымдастыру кезеңі.
а) сәлемдесу ә)оқушыларды түгендеу б) сергіту сәті
Түсіндіру.
2-ге бөлінгіштік белгісі: тек жұп цифрмен аяқталатын сандардың барлығы, тек сол сандар ғана, 2-ге бөлінеді. Мысалы, 123547894 саны 2-ге бөлінеді, өйткені, 4 саны 2-ге бөлінеді; 12354789 саны 2-ге бөлінбейді, өйткені, 9 саны 2-ге бөлінбейді.
3-ке бөлінгіштік белгісі: тек цифрларының қосындысы 3-ке бөлінетін сандар ғана, 3-ке бөлінеді. Мысалы, 123547812 саны 3-ке бөлінеді, өйткені, 1+2+3+5+4+7+8+1+2=33 саны 3-ке бөлінеді, ал 57312427 саны 3-ке бөлінбейді, өйткені 5+7+3+1+2+4+2+7=31 саны 3-ке бөлінбейді.
4-ке бөлінгіштік белгісі: тек соңғы екі цифрымен таңбаланған сан 4-ке бөлінетін сандар ғана, тек сол сандар ғана, 4-ке бөлінеді. Мысалы, 83745656 саны 4-ке бөлінеді, өйткені, 56 саны 4-ке бөлінеді; 5349741414 саны 4-ке бөлінбейді, өйткені, 14 саны 4-ке бөлінбейді.
5-ке бөлінгіштік белгісі: тек соңғы цифрлары 5-ке бөлінетін сандар ғана, тек сол сандар ғана, 5-ке бөлінеді. Мысалы, 278324170 саны 5-ке бөлінеді, өйткені, 0 саны 5-ке бөлінеді; ал 12937234 саны 5-ке бөлінбейді, өйткені, 4 саны 5-ке бөлінбейді.
6-ға бөлінгіштік белгісі: тек 2-ге және 3-ке бөлінетін сандар ғана 6-ға бөлінеді. Мысалы, 10202010 саны 6-ға бөлінеді, өйткені, бұл санның соңғы цифры 0 болатындықтан, 2-ге бөлінеді және 1+0+2+0+2+0+1+0=6 саны 3-ке бөлінеді, ал 2012 саны 6-ға бөлінбейді, өйткені, бұл сан 2-ге бөлінгенімен 3-ке бөлінбейді.
8-ге бөлінгіштік белгісі: тек саны 8-ге бөлінетін сандар ғана, тек сондай сандар ғана 8-ге бөлінеді. Мысалы, 437258112 саны 8-ге бөлінеді, өйткені, 112 саны 8-ге бөлінеді, ал 256124 саны 8-ге бөлінбейді, өйткені, 124 саны 8-ге бөлінбейді.
9-ға бөлінгіштік белгісі: тек цифрларының қосындысы 9-ға бөлінетін сандар ғана, тек сол сандар ғана, 9-ға бөлінеді. Мысалы, 23752827 саны 9-ға бөлінеді, өйткені, 2+3+7+5+2+8+2+7=36 саны 9-ға бөлінеді, ал 1541547179 саны 9-ға бөлінбейді, өйткені, 1+5+4+1+5+4+7+1+7+9=44 саны 9-ға бөлінбейді.
10-ға бөлінгіштік белгісі: тек нольмен аяқталатын сандар ғана, тек сол сандар ғана, 10-ға бөлінеді. Мысалы, 1234567890 саны 10-ға бөлінеді, өйткені, 0 саны 10-ға бөлінеді, ал 2012 саны 10-ға бөлінбейді, өйткені, 2 саны 10-ға бөлінбейді.
11-ге бөлінгіштік белгісі: тек санның құрамындағы тақ орындағы цифрларының қосындысы мен оның жұп орындағы цифрларының қосындысының айырмасы 0-ге тең немесе 11-ге бөлінетін сандар ғана, тек сол сандар ғана, 11-ге бөлінеді. Мысалы, 43715265 саны 11-ге бөлінеді, өйткені, (4+7+5+6)-(3+1+2+5)=22-11=11 саны 11-ге бөлінеді, ал 12922120 саны 11-ге бөлінбейді, өйткені (1+9+2+2)-(2+2+1+0)=14-5=9 саны 11-ге бөлінбейді.
25-ке бөлінгіштік белгісі: тек соңғы екі цифрларымен таңбаланған сан 25-ке бөлінсе немесе сан екі нольмен аяқталса, тек сол сандар ғана 25-ке бөлінеді. Мысалы, 4381997550 саны 25-ке бөлінеді, өйткені, 50 саны 25-ке бөлінеді, ал 1112221740 саны 25-ке бөлінбейді, себебі, 40 саны 25-ке бөлінбейді.
Енді осы анықтамаларды пайдаланып, жоғарыда берілген есепті шығарайық (3-ке бөлінетін түріндегі ең кіші натурал санды табыңдар).
Шешуі: мұндай түрдегі берілген санның цифрларының қосындысы мынаған тең: 1+2+3+4+3+х+у=13+x+y. берілген 3 сан 3-ке бөлінетін бұл қосындының ең кіші мәні 15-ке тең, яғни х+у=2-ге тең. х+у=2 шартын қанағаттандыратын есептің шартында берілген түрдегі сандардың үш түбірі бар: 1230432, 1232430, 1231431, бұлардың ішіндегі ең кішісі а = 1230432-ге тең.
2-ден басқа, берілген түрдегі сандар үшін х+у қосындысы 3-ке бөлінетін мынадай сандар бар: 5, 8, 11, 14, 17.
Егер х+у=5 болса, онда ең кіші сан 1230435-ке тең, ал х+у=8 болса, онда ең кіші санның 1230438-ге тең болатындығы айқын. Бұл табылған екі санның мәні а-дан артық. Бар қалған 3 жағдайларда да (x+y=11, x+y=14, x+y=17) шығатын ең кіші сандардың а санынан артық болатындығына оңай көз жеткізуге болады. Сонымен, ізделінді сан a=1230432-ге тең.
2 мысал: 12 қосындысы қосындысы 3-ке бөлінетін ең үлкен х цифрын анықтау керек болсын.
Шешуі: 12 саны және берілген қосынды 3-ке бөлінетіндіктен, саны олардың айырымы ретінде 3-ке бөлінеді. 5 x 3-ке бөлінетін ең үлкен цифр 7-ге тең, яғни, х 7. Жауабы: х 7.
Ферроль әдісімен көбейту. Көбейтіндінің бірлігін алу үшін көбейткіштердің бірліктерін көбейтеді. Ондығын алу үшін біреуінің ондығын бірлігіне және керісінше көбейтіп, қосындыға ойға алған санды қосады, жүздігін алу үшін ондықтарын көбейтеді. Бұл әдіс мына теңдіктен шығады:
(10а+в)(10с+д)=100ас+10(ад+вс)+вд.
1 мысал: 2738=1026.
а) 7×8=56; 6-ны жазамыз, 5-ті ойға аламыз.
б) 2×8+7×3+5=42, 2 жазылады, 4 ойға алынады.
в) 2×3+4=10.
2 мысал: 12×14=168.
а) 2×4=8.
б) 1×2+1×4=6.
в) 1×1=1.
Осы әдіспен үш орынды санды екі орынды санға да көбейтуге болады.
Мысалы: 125×23=2875.
а) 3×5=15, 5 жазылады, 1 ойға алынады.
б) 2×3+2×5+1=17, 7 жазылады, 1 ойға алынады.
в) 2×2+1×3+1=8,8 жазылады.
г) 2×1=2, 2 жазылады, сонымен нәтиже: 125×23=2875 болады.
Ескерту: мұндағы белгісі көбейту амалын білдіреді.
11 санына шапшаң көбейту әдісі. Есептеуді тездетудің өзгеше бір әдісі – санды 11-ге көбейту әдісімен танысайық. Мысалы, 26-ны 11-ге көбейту керек болсын. Oл үшін әуелі 26 санын құрайтын 2 және 6 цифрларын қосып, 2 шыққан қосындыны 2 және 6 цифрларының арасына «сыналап» енгізіп жазамыз, сонда 286 саны пайда болады.
Cанды құрайтын цифрлардың қосындысы екі таңбалы сан болуы да мүмкін, алғашқы цифры 1 болмақ. Осы 1-ді санның ондық орында жазылған цифрына қосу керек те, цифрлардың арасына қосындының бірлік орындағы цифрын «сыналап» енгізу шарт. Мысалы, 75-ті 11-ге көбейткен кезде 75 санын құрайтын цифрларды қосып, (7+5=12) пайда болған нәтиженің алдыңғы цифрын 7-ге қосамыз. Сонда 85 саны, ал 2 цифрын жаңадан пайда болған 85 санының 8 бен 5 цифрларының арасына «сыналап» ендіріп жазсақ, 825 саны пайда болады.
11-ге лезде көбейту тәсілін мына теңдеуден аңғаруыңызға болады:
(10a+b)11=110a+11b=100a+10b(a+b)+b.


Кейде есеп шығару барысында мынадай есептер жиі кездеседі:
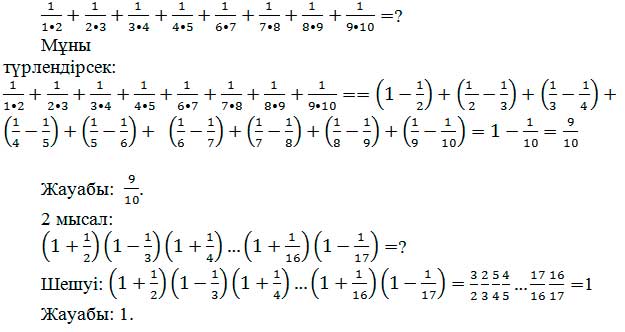
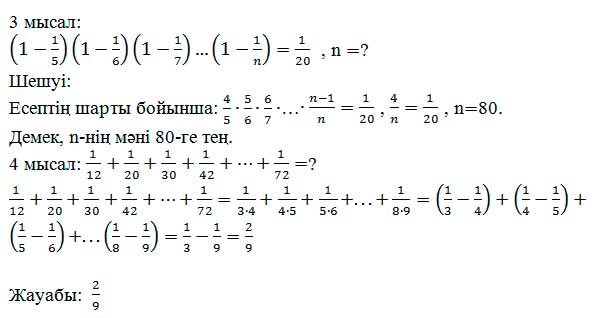
Бұл тәсіл неге негізделгенін анықтау үшін көбейткіштерді мына түрде жазалық:
(1000 14)(1000 3). Және мүшелерді алгебра ережесі бойынша көбейтелік:
1000•1000 1000•14 1000•3+14•3.
Мұны түрлендірейік:
1000(1000 14) 1000•3+14•3=1000•986 +14•3=1000(986 3)+14•3.
Күрделі радикалды түрлендіру арқылы
жылдам есептеу. Мына өрнекті , мұндағы a, b және c қайсыбір
сандар қос радикал немесе күрделі радикал деп атайды.
Күрделі радикалды түрлендіру мына формула арқылы жүзеге
асады:
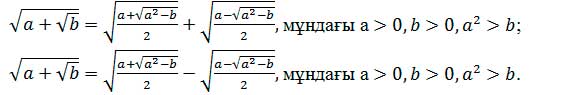
Күрделі радикалы бар өрнектерді түрлендіргенде
көбінесе қос радикалды ішкі радикалдан құтқарып алған тиімді.
Егер түбір астында тұрған өрнек толық квадрат болса, онда оны мына
тепе-теңдікті қолдану арқылы сыртқы радикалдан құтқаруға
болады.
1 мысал:
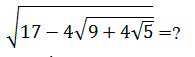
Шешуі: арифметикалық квадрат түбірдің қасиетін пайдаланып табатынымыз:

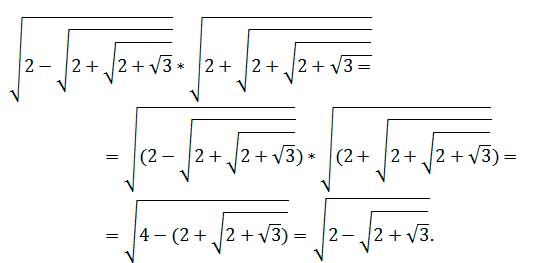


Кейбір есептерді шығарудың тиімді әдістері. Кейде есеп барысында мынадай есептер жиі кездеседі:
a) 100! саны неше нөлмен аяқталады: (100)!= 1*2*3*...*100).
ә) 19821982 саны қай цифрмен аяқталады?
б) 21984 – 11 саны 3-ке бөліне ме?
в) 2100 санының неше цифры бар?
г) Қай сан үлкен: 1020 немесе 2010? 10020 немесе 90010?
д) (2*57 – 5*27)83 – [(2*57)83 – (5*27)83] өрнегі 83-ке бөліне ме?
е) 1110 – 100-ге бөліне ме?
ж) 1010 санының неше бөлгіші бар?
з) 333555+555333 өрнегінің 37-ге бөлінетінін дәлелдеу керек.
Енді осылардың шығарылу жолдарымен танысайық:
a) Шешуі: 100! саны неше нөлмен аяқталады ? (100)!= (1*2*3*...*100).
Әрбір санда 10 көбейткіші неше рет кездессе, сонша нөлмен аяқталады. Бірақ та 10 саны 5 пен 2-нің көбейтіндісіне тең. Сондықтан, ізделуші нөлдер саны мына екі санның ең кіші көбейткішіне: 100! санының жай көбейткіштерге жіктелуіндегі көбейткіштерінің саны 2 мен 5 санына тең.
100! санында 2 саны 5-тен көп рет кездеседі. Сондықтан 100! санының жіктелуіндегі 5-тердің санын анықтау керек болады. 100! санында 5-ке еселік 20 сан, олардың арасында 4-ке еселік 25 сан – олар мына төртеуі: 25, 50, 75 және 100. Олай болса, 100! санының жай көбейткіштерге жіктелуінде 5 саны 24 дәрежеде кездеседі (себебі 20+4=24). Сонымен 100! саны 24 нөлмен аяқталмақ.
ә) Шешуі: 19821982 саны қай цифрмен аяқталады?
1982 санының натурал дәрежесінің соңында қайталанатын цифрларының заңдылығын анықтайық. 1982 саны 2 цифрымен аяқталған, 19822 саны 4 цифрымен, 19823 саны 8 цифрымен, 19824 саны 6 цифрымен, 19825 саны 2 цифрымен аяқталады. 1982 санының натурал дәрежесінің соңғы цифры әрбір төрт дәрежеден соң қайталанатынын анықтадық. 19821982 = 1982495*2 + 2, олай болса, 19821982 саны 19822 секілді 4 цифрымен аяқталады.
б) Шешуі: 21984 – 11 саны 3-ке бөліне ме?
21984 дәрежесін 22*992 деп жазуымызға болады, 22=4, олай болса, бастапқы берілген 21984 санын 4992 деп жаза аламыз. Сондықтан 4992 – 1=(3+1)992 – 1. Енді (3+1)992 биномының барлық жіктелуінің алғашқы 992 мүшесінің қосындысы 3-ке бөлінеді. Жақша ішіндегі 1-дің 992 дәрежесі 1-ге тең болатындықтан ол берілген сандағы 1-мен қосылып, 0 болады. Олай болса, берілген сан 3-ке бөлінеді.
в) Шешуі: 2100 санының неше цифры бар?
2100=х. Теңдікті логорифмдесек, lg x=100 lg 2= 100*0,3010=30,1. Сондықтан берілген 2100 санын жазу үшін 31 цифр қажет екен.
г) Шешуі: қай сан үлкен: 1020 немесе 2010? 10020 немесе 90010?
1) 1020=1010*1010>1010*210; 1020>2010.
2) 10020=10010*10010>9010*1010; 10020>90010.
д) Шешуі: (2*57 – 5*27)83 – [(2*57)83 -( 5*27)83] өрнегі 83-ке бөліне ме?
Бұл өрнектегі жақша ішіндегі 2*5 көбейтінділерін 10-мен алмастырып, бірдей мүшелерді жақша сыртына шығарып ықшамдайтын болсақ:
1083*[(56–26)83–1083*[(56)83–(26)83]=1083*[(56–26)83 – (56)83+(26)83].
Енді (56–26)83-ті Ньютон биномы формуласы бойынша жіктейтін болсақ, жіктелудегі бірінші және соңғы мүшелер биномның дәрежесінен кейінгі мүшелермен жойылып кетеді. Өзге мүшелерінің барлық коэффиценттері 83-ке еселік болатындықтан барлық өрнек 83-ке бөлінеді.
е) Шешуі: 1110 – 100-ге бөліне ме?
Олай болса, бүкіл қосынды 100-ге бөлінеді.
ж) Шешуі: 1010 санының неше бөлгіші бар?
1010=(2*5)10=210*510. Осы көбейтіндінің бөлгіштері 2к *5к болады, k және n – 10 санынан артық емес бүтін оң сандар. Осылар арасында 2-нің дәрежесі түрінде 11 бөлгіш бар: 20, 21, 22, ..., 210, дәл соншама тек 5-тің дәрежелерін қамтитын бөлгіштері бар. 2 санының дәрежесі түріндегі барлық бөлгіштері мен 5-тің дәрежесі түрінде бөлгіштерін өзара көбейтсек, 11*11 = 121 бөлгіші болатынына көзімізді жеткіземіз.
з) Шешуі: 333555 +555333 өрнегінің 37-ге бөлінетінін дәлелдеу керек.
333555 +555333=3555*111555+5333*111333 =111333(3555*111222+5333).
111=3*37 болғандықтан берілген өрнек 37-ге бөлінеді. Берілген өрнектің 111-ге, 111333-ке, 3333-ке, 37333-ке бөлінетіндігін естен шығармау керек.
Үйге тапсырма: мысалдарды орындау
Сабақты қорытындылау.
-
Радикалдың қасиетін түсіндіру.
-
Сандардың еселіктеріне мысал
-
Сандардың бөлінгіштігіне мысал.
Бағалау.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Жоба "Бөлінгіштік белгісі"
Жоба "Бөлінгіштік белгісі"
Тақырыбы: Кейбір сандардың бөлінгіштік белгілері:
Мақсаты:
1)Оқушыларды кейбір сандардың бөлінгіштік белгілері олимпиада есептерінде көптеп кездесетінін түсіндіру.
2)Оқушылардың ой-өрісін кеіейту, математикалық тілін және логикалық ойлау қабілетін дамыту.
3)Оқуға, саналы сезімге, жауапкершілікке өз бетінше еңбектенуге тәрбиелеу.
Сабақ түрі: түсіндірмелі
Көрнекілігі: АКТ, калькулятор
Сабақ барысы: 1.Ұйымдастыру кезеңі.
а) сәлемдесу ә)оқушыларды түгендеу б) сергіту сәті
Түсіндіру.
2-ге бөлінгіштік белгісі: тек жұп цифрмен аяқталатын сандардың барлығы, тек сол сандар ғана, 2-ге бөлінеді. Мысалы, 123547894 саны 2-ге бөлінеді, өйткені, 4 саны 2-ге бөлінеді; 12354789 саны 2-ге бөлінбейді, өйткені, 9 саны 2-ге бөлінбейді.
3-ке бөлінгіштік белгісі: тек цифрларының қосындысы 3-ке бөлінетін сандар ғана, 3-ке бөлінеді. Мысалы, 123547812 саны 3-ке бөлінеді, өйткені, 1+2+3+5+4+7+8+1+2=33 саны 3-ке бөлінеді, ал 57312427 саны 3-ке бөлінбейді, өйткені 5+7+3+1+2+4+2+7=31 саны 3-ке бөлінбейді.
4-ке бөлінгіштік белгісі: тек соңғы екі цифрымен таңбаланған сан 4-ке бөлінетін сандар ғана, тек сол сандар ғана, 4-ке бөлінеді. Мысалы, 83745656 саны 4-ке бөлінеді, өйткені, 56 саны 4-ке бөлінеді; 5349741414 саны 4-ке бөлінбейді, өйткені, 14 саны 4-ке бөлінбейді.
5-ке бөлінгіштік белгісі: тек соңғы цифрлары 5-ке бөлінетін сандар ғана, тек сол сандар ғана, 5-ке бөлінеді. Мысалы, 278324170 саны 5-ке бөлінеді, өйткені, 0 саны 5-ке бөлінеді; ал 12937234 саны 5-ке бөлінбейді, өйткені, 4 саны 5-ке бөлінбейді.
6-ға бөлінгіштік белгісі: тек 2-ге және 3-ке бөлінетін сандар ғана 6-ға бөлінеді. Мысалы, 10202010 саны 6-ға бөлінеді, өйткені, бұл санның соңғы цифры 0 болатындықтан, 2-ге бөлінеді және 1+0+2+0+2+0+1+0=6 саны 3-ке бөлінеді, ал 2012 саны 6-ға бөлінбейді, өйткені, бұл сан 2-ге бөлінгенімен 3-ке бөлінбейді.
8-ге бөлінгіштік белгісі: тек саны 8-ге бөлінетін сандар ғана, тек сондай сандар ғана 8-ге бөлінеді. Мысалы, 437258112 саны 8-ге бөлінеді, өйткені, 112 саны 8-ге бөлінеді, ал 256124 саны 8-ге бөлінбейді, өйткені, 124 саны 8-ге бөлінбейді.
9-ға бөлінгіштік белгісі: тек цифрларының қосындысы 9-ға бөлінетін сандар ғана, тек сол сандар ғана, 9-ға бөлінеді. Мысалы, 23752827 саны 9-ға бөлінеді, өйткені, 2+3+7+5+2+8+2+7=36 саны 9-ға бөлінеді, ал 1541547179 саны 9-ға бөлінбейді, өйткені, 1+5+4+1+5+4+7+1+7+9=44 саны 9-ға бөлінбейді.
10-ға бөлінгіштік белгісі: тек нольмен аяқталатын сандар ғана, тек сол сандар ғана, 10-ға бөлінеді. Мысалы, 1234567890 саны 10-ға бөлінеді, өйткені, 0 саны 10-ға бөлінеді, ал 2012 саны 10-ға бөлінбейді, өйткені, 2 саны 10-ға бөлінбейді.
11-ге бөлінгіштік белгісі: тек санның құрамындағы тақ орындағы цифрларының қосындысы мен оның жұп орындағы цифрларының қосындысының айырмасы 0-ге тең немесе 11-ге бөлінетін сандар ғана, тек сол сандар ғана, 11-ге бөлінеді. Мысалы, 43715265 саны 11-ге бөлінеді, өйткені, (4+7+5+6)-(3+1+2+5)=22-11=11 саны 11-ге бөлінеді, ал 12922120 саны 11-ге бөлінбейді, өйткені (1+9+2+2)-(2+2+1+0)=14-5=9 саны 11-ге бөлінбейді.
25-ке бөлінгіштік белгісі: тек соңғы екі цифрларымен таңбаланған сан 25-ке бөлінсе немесе сан екі нольмен аяқталса, тек сол сандар ғана 25-ке бөлінеді. Мысалы, 4381997550 саны 25-ке бөлінеді, өйткені, 50 саны 25-ке бөлінеді, ал 1112221740 саны 25-ке бөлінбейді, себебі, 40 саны 25-ке бөлінбейді.
Енді осы анықтамаларды пайдаланып, жоғарыда берілген есепті шығарайық (3-ке бөлінетін түріндегі ең кіші натурал санды табыңдар).
Шешуі: мұндай түрдегі берілген санның цифрларының қосындысы мынаған тең: 1+2+3+4+3+х+у=13+x+y. берілген 3 сан 3-ке бөлінетін бұл қосындының ең кіші мәні 15-ке тең, яғни х+у=2-ге тең. х+у=2 шартын қанағаттандыратын есептің шартында берілген түрдегі сандардың үш түбірі бар: 1230432, 1232430, 1231431, бұлардың ішіндегі ең кішісі а = 1230432-ге тең.
2-ден басқа, берілген түрдегі сандар үшін х+у қосындысы 3-ке бөлінетін мынадай сандар бар: 5, 8, 11, 14, 17.
Егер х+у=5 болса, онда ең кіші сан 1230435-ке тең, ал х+у=8 болса, онда ең кіші санның 1230438-ге тең болатындығы айқын. Бұл табылған екі санның мәні а-дан артық. Бар қалған 3 жағдайларда да (x+y=11, x+y=14, x+y=17) шығатын ең кіші сандардың а санынан артық болатындығына оңай көз жеткізуге болады. Сонымен, ізделінді сан a=1230432-ге тең.
2 мысал: 12 қосындысы қосындысы 3-ке бөлінетін ең үлкен х цифрын анықтау керек болсын.
Шешуі: 12 саны және берілген қосынды 3-ке бөлінетіндіктен, саны олардың айырымы ретінде 3-ке бөлінеді. 5 x 3-ке бөлінетін ең үлкен цифр 7-ге тең, яғни, х 7. Жауабы: х 7.
Ферроль әдісімен көбейту. Көбейтіндінің бірлігін алу үшін көбейткіштердің бірліктерін көбейтеді. Ондығын алу үшін біреуінің ондығын бірлігіне және керісінше көбейтіп, қосындыға ойға алған санды қосады, жүздігін алу үшін ондықтарын көбейтеді. Бұл әдіс мына теңдіктен шығады:
(10а+в)(10с+д)=100ас+10(ад+вс)+вд.
1 мысал: 2738=1026.
а) 7×8=56; 6-ны жазамыз, 5-ті ойға аламыз.
б) 2×8+7×3+5=42, 2 жазылады, 4 ойға алынады.
в) 2×3+4=10.
2 мысал: 12×14=168.
а) 2×4=8.
б) 1×2+1×4=6.
в) 1×1=1.
Осы әдіспен үш орынды санды екі орынды санға да көбейтуге болады.
Мысалы: 125×23=2875.
а) 3×5=15, 5 жазылады, 1 ойға алынады.
б) 2×3+2×5+1=17, 7 жазылады, 1 ойға алынады.
в) 2×2+1×3+1=8,8 жазылады.
г) 2×1=2, 2 жазылады, сонымен нәтиже: 125×23=2875 болады.
Ескерту: мұндағы белгісі көбейту амалын білдіреді.
11 санына шапшаң көбейту әдісі. Есептеуді тездетудің өзгеше бір әдісі – санды 11-ге көбейту әдісімен танысайық. Мысалы, 26-ны 11-ге көбейту керек болсын. Oл үшін әуелі 26 санын құрайтын 2 және 6 цифрларын қосып, 2 шыққан қосындыны 2 және 6 цифрларының арасына «сыналап» енгізіп жазамыз, сонда 286 саны пайда болады.
Cанды құрайтын цифрлардың қосындысы екі таңбалы сан болуы да мүмкін, алғашқы цифры 1 болмақ. Осы 1-ді санның ондық орында жазылған цифрына қосу керек те, цифрлардың арасына қосындының бірлік орындағы цифрын «сыналап» енгізу шарт. Мысалы, 75-ті 11-ге көбейткен кезде 75 санын құрайтын цифрларды қосып, (7+5=12) пайда болған нәтиженің алдыңғы цифрын 7-ге қосамыз. Сонда 85 саны, ал 2 цифрын жаңадан пайда болған 85 санының 8 бен 5 цифрларының арасына «сыналап» ендіріп жазсақ, 825 саны пайда болады.
11-ге лезде көбейту тәсілін мына теңдеуден аңғаруыңызға болады:
(10a+b)11=110a+11b=100a+10b(a+b)+b.


Кейде есеп шығару барысында мынадай есептер жиі кездеседі:
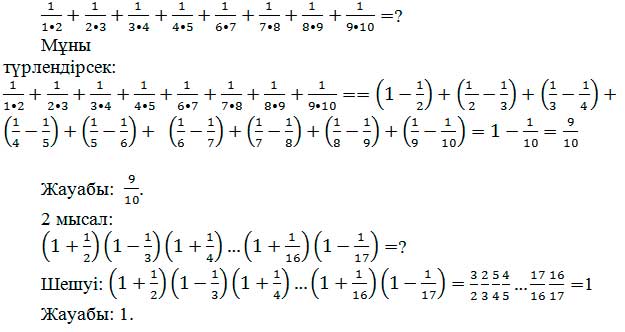
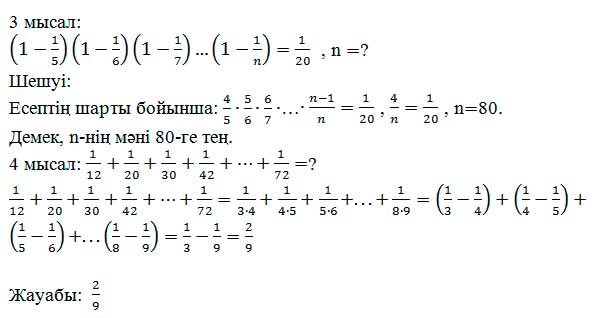
Бұл тәсіл неге негізделгенін анықтау үшін көбейткіштерді мына түрде жазалық:
(1000 14)(1000 3). Және мүшелерді алгебра ережесі бойынша көбейтелік:
1000•1000 1000•14 1000•3+14•3.
Мұны түрлендірейік:
1000(1000 14) 1000•3+14•3=1000•986 +14•3=1000(986 3)+14•3.
Күрделі радикалды түрлендіру арқылы
жылдам есептеу. Мына өрнекті , мұндағы a, b және c қайсыбір
сандар қос радикал немесе күрделі радикал деп атайды.
Күрделі радикалды түрлендіру мына формула арқылы жүзеге
асады:
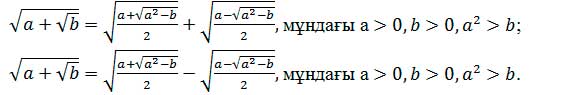
Күрделі радикалы бар өрнектерді түрлендіргенде
көбінесе қос радикалды ішкі радикалдан құтқарып алған тиімді.
Егер түбір астында тұрған өрнек толық квадрат болса, онда оны мына
тепе-теңдікті қолдану арқылы сыртқы радикалдан құтқаруға
болады.
1 мысал:
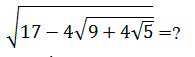
Шешуі: арифметикалық квадрат түбірдің қасиетін пайдаланып табатынымыз:

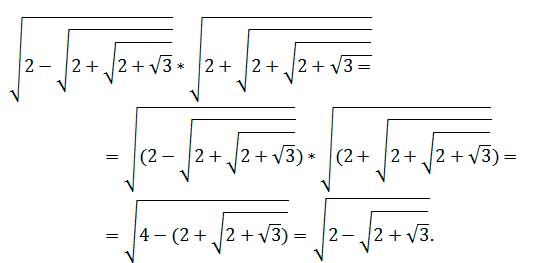


Кейбір есептерді шығарудың тиімді әдістері. Кейде есеп барысында мынадай есептер жиі кездеседі:
a) 100! саны неше нөлмен аяқталады: (100)!= 1*2*3*...*100).
ә) 19821982 саны қай цифрмен аяқталады?
б) 21984 – 11 саны 3-ке бөліне ме?
в) 2100 санының неше цифры бар?
г) Қай сан үлкен: 1020 немесе 2010? 10020 немесе 90010?
д) (2*57 – 5*27)83 – [(2*57)83 – (5*27)83] өрнегі 83-ке бөліне ме?
е) 1110 – 100-ге бөліне ме?
ж) 1010 санының неше бөлгіші бар?
з) 333555+555333 өрнегінің 37-ге бөлінетінін дәлелдеу керек.
Енді осылардың шығарылу жолдарымен танысайық:
a) Шешуі: 100! саны неше нөлмен аяқталады ? (100)!= (1*2*3*...*100).
Әрбір санда 10 көбейткіші неше рет кездессе, сонша нөлмен аяқталады. Бірақ та 10 саны 5 пен 2-нің көбейтіндісіне тең. Сондықтан, ізделуші нөлдер саны мына екі санның ең кіші көбейткішіне: 100! санының жай көбейткіштерге жіктелуіндегі көбейткіштерінің саны 2 мен 5 санына тең.
100! санында 2 саны 5-тен көп рет кездеседі. Сондықтан 100! санының жіктелуіндегі 5-тердің санын анықтау керек болады. 100! санында 5-ке еселік 20 сан, олардың арасында 4-ке еселік 25 сан – олар мына төртеуі: 25, 50, 75 және 100. Олай болса, 100! санының жай көбейткіштерге жіктелуінде 5 саны 24 дәрежеде кездеседі (себебі 20+4=24). Сонымен 100! саны 24 нөлмен аяқталмақ.
ә) Шешуі: 19821982 саны қай цифрмен аяқталады?
1982 санының натурал дәрежесінің соңында қайталанатын цифрларының заңдылығын анықтайық. 1982 саны 2 цифрымен аяқталған, 19822 саны 4 цифрымен, 19823 саны 8 цифрымен, 19824 саны 6 цифрымен, 19825 саны 2 цифрымен аяқталады. 1982 санының натурал дәрежесінің соңғы цифры әрбір төрт дәрежеден соң қайталанатынын анықтадық. 19821982 = 1982495*2 + 2, олай болса, 19821982 саны 19822 секілді 4 цифрымен аяқталады.
б) Шешуі: 21984 – 11 саны 3-ке бөліне ме?
21984 дәрежесін 22*992 деп жазуымызға болады, 22=4, олай болса, бастапқы берілген 21984 санын 4992 деп жаза аламыз. Сондықтан 4992 – 1=(3+1)992 – 1. Енді (3+1)992 биномының барлық жіктелуінің алғашқы 992 мүшесінің қосындысы 3-ке бөлінеді. Жақша ішіндегі 1-дің 992 дәрежесі 1-ге тең болатындықтан ол берілген сандағы 1-мен қосылып, 0 болады. Олай болса, берілген сан 3-ке бөлінеді.
в) Шешуі: 2100 санының неше цифры бар?
2100=х. Теңдікті логорифмдесек, lg x=100 lg 2= 100*0,3010=30,1. Сондықтан берілген 2100 санын жазу үшін 31 цифр қажет екен.
г) Шешуі: қай сан үлкен: 1020 немесе 2010? 10020 немесе 90010?
1) 1020=1010*1010>1010*210; 1020>2010.
2) 10020=10010*10010>9010*1010; 10020>90010.
д) Шешуі: (2*57 – 5*27)83 – [(2*57)83 -( 5*27)83] өрнегі 83-ке бөліне ме?
Бұл өрнектегі жақша ішіндегі 2*5 көбейтінділерін 10-мен алмастырып, бірдей мүшелерді жақша сыртына шығарып ықшамдайтын болсақ:
1083*[(56–26)83–1083*[(56)83–(26)83]=1083*[(56–26)83 – (56)83+(26)83].
Енді (56–26)83-ті Ньютон биномы формуласы бойынша жіктейтін болсақ, жіктелудегі бірінші және соңғы мүшелер биномның дәрежесінен кейінгі мүшелермен жойылып кетеді. Өзге мүшелерінің барлық коэффиценттері 83-ке еселік болатындықтан барлық өрнек 83-ке бөлінеді.
е) Шешуі: 1110 – 100-ге бөліне ме?
Олай болса, бүкіл қосынды 100-ге бөлінеді.
ж) Шешуі: 1010 санының неше бөлгіші бар?
1010=(2*5)10=210*510. Осы көбейтіндінің бөлгіштері 2к *5к болады, k және n – 10 санынан артық емес бүтін оң сандар. Осылар арасында 2-нің дәрежесі түрінде 11 бөлгіш бар: 20, 21, 22, ..., 210, дәл соншама тек 5-тің дәрежелерін қамтитын бөлгіштері бар. 2 санының дәрежесі түріндегі барлық бөлгіштері мен 5-тің дәрежесі түрінде бөлгіштерін өзара көбейтсек, 11*11 = 121 бөлгіші болатынына көзімізді жеткіземіз.
з) Шешуі: 333555 +555333 өрнегінің 37-ге бөлінетінін дәлелдеу керек.
333555 +555333=3555*111555+5333*111333 =111333(3555*111222+5333).
111=3*37 болғандықтан берілген өрнек 37-ге бөлінеді. Берілген өрнектің 111-ге, 111333-ке, 3333-ке, 37333-ке бөлінетіндігін естен шығармау керек.
Үйге тапсырма: мысалдарды орындау
Сабақты қорытындылау.
-
Радикалдың қасиетін түсіндіру.
-
Сандардың еселіктеріне мысал
-
Сандардың бөлінгіштігіне мысал.
Бағалау.

шағым қалдыра аласыз















