ОТДЕЛ ОБРАЗОВАНИЯ МАРТУКСКОГО РАЙОНА
РАЙОННЫЙ МЕТОДИЧЕСКИЙ КАБИНЕТ
Методическое пособие
по математике по теме: «Проценты»

Составитель: учитель математики
Дәніш Ә.Е.
Мартук, 2021 год
Рассмотрено на заседании районного методического совета
«___» ___________20___г
Заведующий методическим кабинетом отдела образования Мартукского района: __________________ Балмагамбетова С.Х.
Составитель: учитель математики Казанской общеобразовательной основной школы Дәніш Әсем Еділқызы
Рецензент: Антипова Райля Абдулловна – методист отдела образования Мартукского района
В данном пособии собраны материалы по решению задач на нахождения процента от числа, числа по его проценту, а также практических задач на применение свойств процента.
Пояснительная записка.
«Числа управляют миром», – говорили пифагорейцы.
Но числа дают возможность человеку управлять миром,
и в этом нас убеждает весь ход развития науки и техники наших дней.
(А. Дородницын)
Современные дети растут в условиях интенсивно формирующейся рыночной экономики страны. Для них необходимыми стали знания таких областей наук, как экономика, маркетинг, управление, потому что профессии, которые они получат на основе этих знаний, будут не только престижны, но и высокооплачиваемые.
Тема «Проценты» изучается в курсе математики 5, 6 классов. Для усвоения данной темы школьникам необходимо иметь достаточный уровень развития абстрактного мышления, но в возрасте 10-11 лет абстрактное мышление еще недостаточно развито, поэтому учащиеся 5, 6 классов усваивают проценты с трудом. В последующих классах в действующих учебниках алгебры проценты встречаются крайне редко, и каждый раз вызывают большие затруднения у школьников. Это особенно становится заметным при организации повторения в процессе подготовки к итоговой аттестации за курс девятого класса: даже стандартные задачи, взятые из «Экзаменационного сборника» вызывают затруднения у большинства учащихся.
Велика также роль процентов в повседневной жизни, очень часто приходится решать задачу типа «Товар стоит а рублей, потом его цену снизили на р %, затем еще на b %. Сколько стал стоить товар? Решение даже этой простейшей задачи на проценты у многих вызывает затруднение.
В программу старших классов по математике тема «Проценты» не входит, навыки работы с процентами забываются. В основном с задачами на проценты учащиеся сталкиваются на уроках химии и решают их с помощью пропорций, поэтому учащиеся не видят универсальность процентов и не могут решать простейшие задачи на проценты, встречающиеся в другой сфере деятельности человека.
Требование вузов к математической подготовке с каждым годом возрастают. Экзамен по математике в любой вуз всегда содержит задачи на проценты. Уровень требований, предъявляемый к абитуриентам по данной теме, высок. На вступительных экзаменах по математике предлагаются задачи на «сплавы», «смеси», «концентрации», задачи экономического содержания, которые решаются с помощью сложных процентов, а школьная программа не содержит задач такого типа.
Введение.
Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Ныне процент — это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента. В школьном учебнике "Математика, 5 «авторов Н.Я. Виленкина и др. дана еще одна любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.
Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
В вариантах вступительных экзаменов встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема «Проценты» изучается в младших 5-6 классах.
Решение задач на проценты и процентное содержание, концентрацию, смеси и сплавы с преимущественным использованием основных правил действия с десятичными и обыкновенными дробями.
Цель работы: Составить практическое пособие по решению задач на проценты для школьников.
Задачи:
-
Изучить исторический и теоретический материал по интересующему вопросу.
-
Систематизировать задачи на проценты по типам.
-
Составить практические рекомендации по решению задач на проценты.
-
Выявить практическое применение таких задач.
-
Определить план дальнейшей работы над темой.
Практическая значимость работы. Данное пособие по решению задач на проценты будет интересно не только школьникам 5-6 класса, которым интересна математика. Здесь найдут много полезного и выпускники школ, и абитуриенты при подготовке к выпускным и вступительным экзаменам.
Основные типы задач по теме «Проценты».
В данной главе приводятся примеры задач, которые решаются с применением определения, что такое один процент, как выразить дробь в процентах и правилам нахождения части (дроби) от числа, и числа по значению его части (дроби), т.е. это те темы и задачи, которые рассматриваются в школе.
Обращаем внимание, что существуют и другие способы решения простейших задач на проценты, например, составляют пропорции на каждом шаге, но в этом случае решение становится на несколько шагов длиннее. Мы же видим свою задачу в нахождении более быстрых способов решения таких задач, в связи с тем, что в настоящее время редкий тест по математике для абитуриентов, обходится без задач, в которых не упоминались бы проценты.
1.1. Решение задач на применение основных понятий о процентах.
Сотая часть метра — это сантиметр, сотая часть рубля — копейка, сотая часть центнера — килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название — процент. Значит одна копейка — один процент от одного рубля, а один сантиметр — один процент от одного метра.
Один процент — это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.
Определение одного процента можно записать равенством: 1 % = 0,01 * а
5%=0,05, 23%=0,23, 130%=1,3 и т. Д
Как найти 1% от числа? Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.
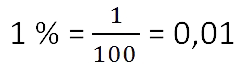
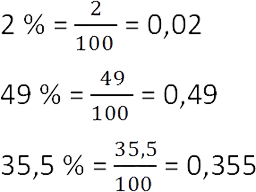
Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак «%».
0,14 = 0,14 · 100% = 14%
0,07 = 0,07 · 100% = 7%
0,565 = 0,565 · 100% = 56,5%
Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь.
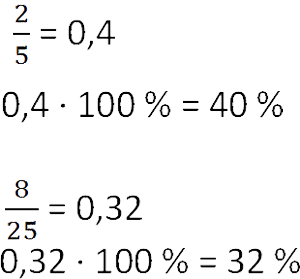
Как вы поняли, проценты тесно связаны с обыкновенными и десятичными дробями. Поэтому стоит запомнить несколько простых равенств.
В повседневной жизни нужно знать о числовой связи дробей и процентов. Так, половина — 50%, четверть — 25%, три четверти — 75%, одна пятая — 20%, а три пятых — 60%.
Знание наизусть соотношений из таблицы внизу облегчит вам решение многих задач.
1 = 100%
|
Картинка |
Обыкновенная дробь |
Десятичная дробь |
Процент |
|||
|
|
|
0,5 |
50% |
|||
|
|
|
0,25 |
25% |
|||
|
|
|
0,75 |
75% |
|||
|
|
|
0,2 |
20% |
|||
|
|
|
0,4 |
40% |
|||
|
|
|
0,6 |
60% |
|||
|
|
|
0,1 |
10% |
|||
|
|
|
0,05 |
5% |
Пример. Найти: 35% от 120.
Решение:
1) 35% = 0,35;
2) 120 * 0,35 = 42.
Ответ: 42.
Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь
Пример. Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше. На сколько процентов повысилась производительность труда токаря?
Решение:
Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от 40. Для этого найдем сначала, какую часть составляет число 10 от числа 40. Мы знаем, что нужно разделить 10 на 40. Получится 0,25. А теперь запишем в процентах — 25%.
Получаем ответ: производительность труда токаря повысилась на 25%.
Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Пример. При плановом задании 60 автомобилей в
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Методическое пособие "Проценты"
Методическое пособие "Проценты"
ОТДЕЛ ОБРАЗОВАНИЯ МАРТУКСКОГО РАЙОНА
РАЙОННЫЙ МЕТОДИЧЕСКИЙ КАБИНЕТ
Методическое пособие
по математике по теме: «Проценты»

Составитель: учитель математики
Дәніш Ә.Е.
Мартук, 2021 год
Рассмотрено на заседании районного методического совета
«___» ___________20___г
Заведующий методическим кабинетом отдела образования Мартукского района: __________________ Балмагамбетова С.Х.
Составитель: учитель математики Казанской общеобразовательной основной школы Дәніш Әсем Еділқызы
Рецензент: Антипова Райля Абдулловна – методист отдела образования Мартукского района
В данном пособии собраны материалы по решению задач на нахождения процента от числа, числа по его проценту, а также практических задач на применение свойств процента.
Пояснительная записка.
«Числа управляют миром», – говорили пифагорейцы.
Но числа дают возможность человеку управлять миром,
и в этом нас убеждает весь ход развития науки и техники наших дней.
(А. Дородницын)
Современные дети растут в условиях интенсивно формирующейся рыночной экономики страны. Для них необходимыми стали знания таких областей наук, как экономика, маркетинг, управление, потому что профессии, которые они получат на основе этих знаний, будут не только престижны, но и высокооплачиваемые.
Тема «Проценты» изучается в курсе математики 5, 6 классов. Для усвоения данной темы школьникам необходимо иметь достаточный уровень развития абстрактного мышления, но в возрасте 10-11 лет абстрактное мышление еще недостаточно развито, поэтому учащиеся 5, 6 классов усваивают проценты с трудом. В последующих классах в действующих учебниках алгебры проценты встречаются крайне редко, и каждый раз вызывают большие затруднения у школьников. Это особенно становится заметным при организации повторения в процессе подготовки к итоговой аттестации за курс девятого класса: даже стандартные задачи, взятые из «Экзаменационного сборника» вызывают затруднения у большинства учащихся.
Велика также роль процентов в повседневной жизни, очень часто приходится решать задачу типа «Товар стоит а рублей, потом его цену снизили на р %, затем еще на b %. Сколько стал стоить товар? Решение даже этой простейшей задачи на проценты у многих вызывает затруднение.
В программу старших классов по математике тема «Проценты» не входит, навыки работы с процентами забываются. В основном с задачами на проценты учащиеся сталкиваются на уроках химии и решают их с помощью пропорций, поэтому учащиеся не видят универсальность процентов и не могут решать простейшие задачи на проценты, встречающиеся в другой сфере деятельности человека.
Требование вузов к математической подготовке с каждым годом возрастают. Экзамен по математике в любой вуз всегда содержит задачи на проценты. Уровень требований, предъявляемый к абитуриентам по данной теме, высок. На вступительных экзаменах по математике предлагаются задачи на «сплавы», «смеси», «концентрации», задачи экономического содержания, которые решаются с помощью сложных процентов, а школьная программа не содержит задач такого типа.
Введение.
Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Ныне процент — это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента. В школьном учебнике "Математика, 5 «авторов Н.Я. Виленкина и др. дана еще одна любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.
Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
В вариантах вступительных экзаменов встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема «Проценты» изучается в младших 5-6 классах.
Решение задач на проценты и процентное содержание, концентрацию, смеси и сплавы с преимущественным использованием основных правил действия с десятичными и обыкновенными дробями.
Цель работы: Составить практическое пособие по решению задач на проценты для школьников.
Задачи:
-
Изучить исторический и теоретический материал по интересующему вопросу.
-
Систематизировать задачи на проценты по типам.
-
Составить практические рекомендации по решению задач на проценты.
-
Выявить практическое применение таких задач.
-
Определить план дальнейшей работы над темой.
Практическая значимость работы. Данное пособие по решению задач на проценты будет интересно не только школьникам 5-6 класса, которым интересна математика. Здесь найдут много полезного и выпускники школ, и абитуриенты при подготовке к выпускным и вступительным экзаменам.
Основные типы задач по теме «Проценты».
В данной главе приводятся примеры задач, которые решаются с применением определения, что такое один процент, как выразить дробь в процентах и правилам нахождения части (дроби) от числа, и числа по значению его части (дроби), т.е. это те темы и задачи, которые рассматриваются в школе.
Обращаем внимание, что существуют и другие способы решения простейших задач на проценты, например, составляют пропорции на каждом шаге, но в этом случае решение становится на несколько шагов длиннее. Мы же видим свою задачу в нахождении более быстрых способов решения таких задач, в связи с тем, что в настоящее время редкий тест по математике для абитуриентов, обходится без задач, в которых не упоминались бы проценты.
1.1. Решение задач на применение основных понятий о процентах.
Сотая часть метра — это сантиметр, сотая часть рубля — копейка, сотая часть центнера — килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название — процент. Значит одна копейка — один процент от одного рубля, а один сантиметр — один процент от одного метра.
Один процент — это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.
Определение одного процента можно записать равенством: 1 % = 0,01 * а
5%=0,05, 23%=0,23, 130%=1,3 и т. Д
Как найти 1% от числа? Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.
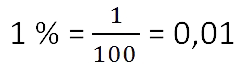
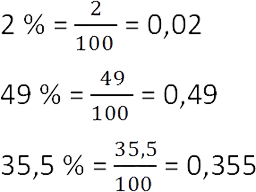
Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак «%».
0,14 = 0,14 · 100% = 14%
0,07 = 0,07 · 100% = 7%
0,565 = 0,565 · 100% = 56,5%
Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь.
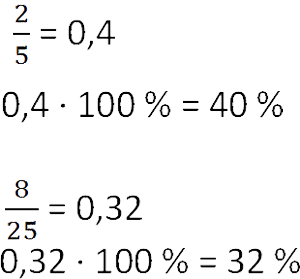
Как вы поняли, проценты тесно связаны с обыкновенными и десятичными дробями. Поэтому стоит запомнить несколько простых равенств.
В повседневной жизни нужно знать о числовой связи дробей и процентов. Так, половина — 50%, четверть — 25%, три четверти — 75%, одна пятая — 20%, а три пятых — 60%.
Знание наизусть соотношений из таблицы внизу облегчит вам решение многих задач.
1 = 100%
|
Картинка |
Обыкновенная дробь |
Десятичная дробь |
Процент |
|||
|
|
|
0,5 |
50% |
|||
|
|
|
0,25 |
25% |
|||
|
|
|
0,75 |
75% |
|||
|
|
|
0,2 |
20% |
|||
|
|
|
0,4 |
40% |
|||
|
|
|
0,6 |
60% |
|||
|
|
|
0,1 |
10% |
|||
|
|
|
0,05 |
5% |
Пример. Найти: 35% от 120.
Решение:
1) 35% = 0,35;
2) 120 * 0,35 = 42.
Ответ: 42.
Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь
Пример. Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше. На сколько процентов повысилась производительность труда токаря?
Решение:
Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от 40. Для этого найдем сначала, какую часть составляет число 10 от числа 40. Мы знаем, что нужно разделить 10 на 40. Получится 0,25. А теперь запишем в процентах — 25%.
Получаем ответ: производительность труда токаря повысилась на 25%.
Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Пример. При плановом задании 60 автомобилей в

шағым қалдыра аласыз