Прямая и обратная пропорциональные зависимости.

Тема: Прямая и обратная пропорциональные зависимости.

Урок 1

Цель: ввести понятие прямой пропорциональной зависимости и научить решать задачи, используя прямо пропорциональную зависимость величин.

Задачи:

1. Образовательная: Познакомить учащихся с понятием прямой пропорциональной зависимости и научить решать задачи, используя прямо пропорциональную зависимость величин, закрепить навыки решения уравнений с помощью пропорции.

2. Развивающая: Развивать память, внимание, воображение, образное и логическое мышление.

3. Воспитательная: Воспитывать интерес к предмету, коллективизм, дисциплинированность.

Оборудование: учебник математики 5 класс (Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд)

Ход урока

I. Повторение ранее изученного материала.

1. Что такое пропорция?

2. Как называются числа х и у в пропорции х : а = в : у?

3. Как называются числа m и n в пропорции а : m = n : в?

4. Сформулируйте основное свойство пропорции? Приведите свои примеры.

5. Решите уравнения:

а) 21 : х = 36 : 12; б) х : 30 = 54 : 40; в)

II. Изучение нового материала.

1. Рассмотреть решение задачи:

За каждый час велосипедист проезжает 12 км. Какой путь он проедет за 1 ч, за 2 ч, за 3 ч, за 4 ч?

Решение.

t = 1 ч, то S = 12 км;

t = 2 ч, то S = 24 км;

t = 3 ч, то S = 36 км;

t = 4 ч, то S = 48 км.

Мы видим, что при увеличении одной величины (времени) в 2, 3, 4 раза значение другой величины тоже увеличивается в 2, 3, 4 раза. Такие величины называют прямо пропорциональными величинами.

2. Разобрать решение задачи по учебнику пункта 22 на странице 128 (об изготовлении деталей станком с числовым программным управлением).

3. Определение прямо пропорциональных величин.

4. Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

5. Задачи на прямо пропорциональные величины можно решать с помощью пропорции.

Задача. За 1,6 ч мальчик прошел 6,4 км. Сколько километров пройдет мальчик за 2,8 ч при той же скорости?

Решение.

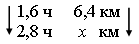
Зависимость между временем и пройденным расстоянием при постоянной скорости прямо пропорциональная, так как с увеличением времени пройденный путь увеличится во столько же раз.

Запишем пропорцию:

Ответ: 11,2 км.

6. Разобрать решение задачи 1 по учебнику на страницах 12–129.

III. Закрепление изученного материала.

1. Решить устно № 782 (а; б; г).

2. Решить письменно задачу № 783 на доске и в тетрадях.

Решение.

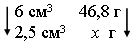
Ответ: 19,5 г.

3. Решить задачу № 784 самостоятельно.

Решение.

Ответ: 1,7 кг.

4. Найти неизвестный член пропорции (с комментированием на месте).

1) у : 7,2 = 75 : 30 2) 0,01 : у = 3,5 : 7.

5. Решить задачу самостоятельно:

Со 125 гусей получают 4 кг пуха. Сколько пуха можно получить с 875 гусей?

Решение.

I способ.

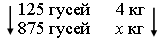
Ответ: 28 кг.

II способ.

1) 875 : 125 = 7 (раз) гусей больше.

2) 4 · 7 = 28 (кг) пуха можно получить.

Ответ: 28 кг.

IV. Итог урока.

1. Какие величины называют прямо пропорциональными?

2. Что можно сказать об отношениях соответствующих значений таких величин?

3. Приведите примеры прямо пропорциональных величин.

Домашнее задание: изучить п. 22 (1-я часть); решить № 811, № 813, № 819 (б).