Назар аударыңыз. Бұл материалды сайт қолданушысы жариялаған. Егер материал сіздің авторлық құқығыңызды бұзса, осында жазыңыз. Біз ең жылдам уақытта материалды сайттан өшіреміз
Жақын арада сайт әкімшілігі сізбен хабарласады

Бонусты жинап картаңызға (kaspi Gold, Halyk bank) шығарып аласыз


ҚМЖ 2 Тоқсан геометрия 11-сынып ЖМБ
Дипломдар мен сертификаттарды алып үлгеріңіз!


Материалдың толық нұсқасын
жүктеп алып көруге болады
|
Ұзақ мерзімді жоспар бөлімі: |
Көпжақтар |
|
Педагогтің Аты,Тегі, Әкесінің аты |
Абдуллаева Д |
|
Күні: |
05/11/24 |
|
Сыныбы: 11ә |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
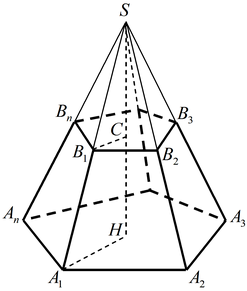
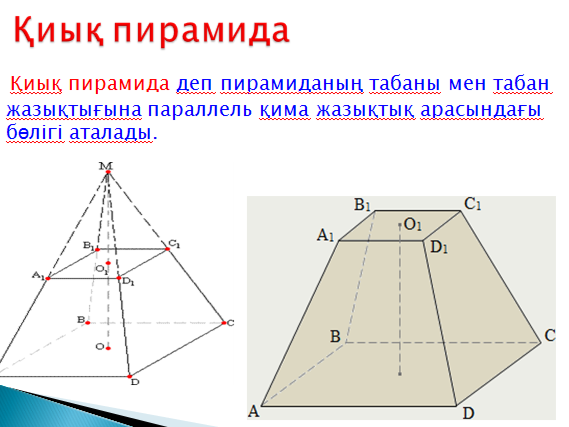
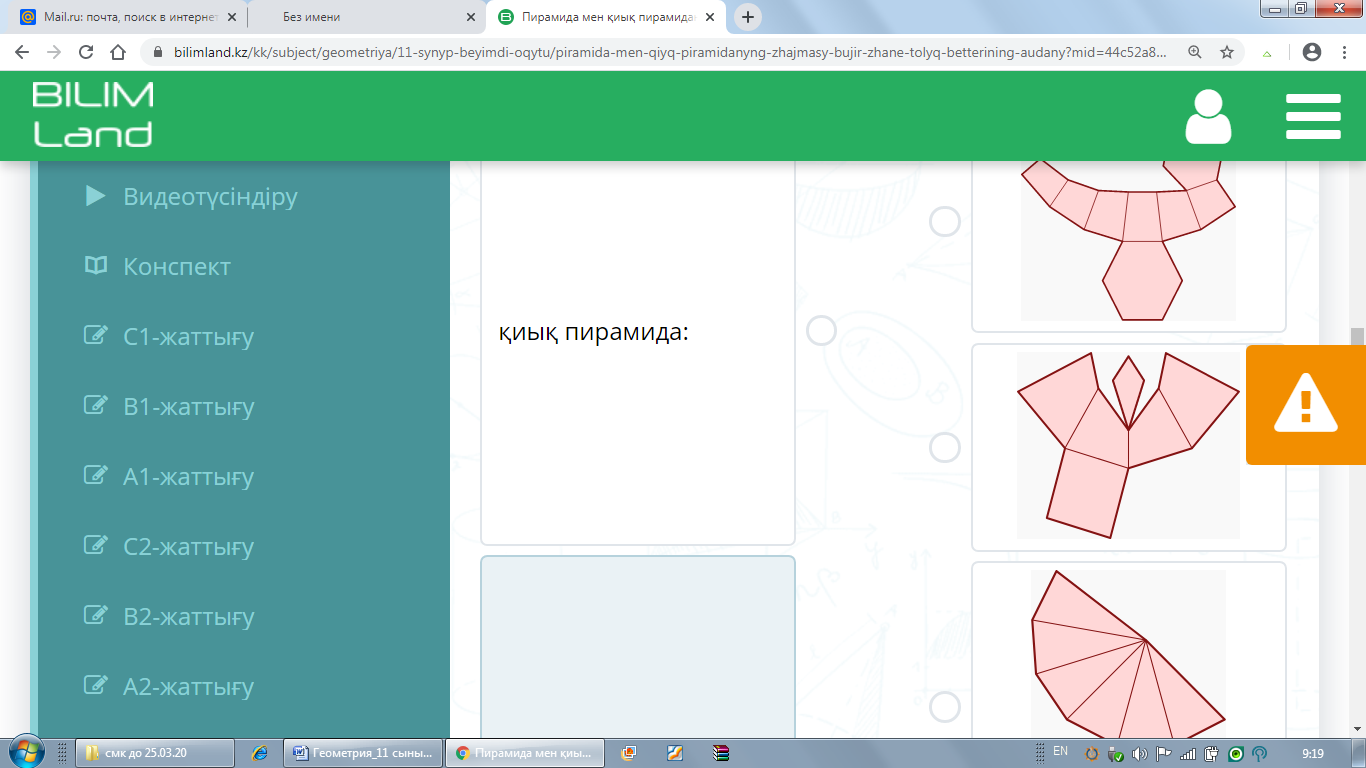
Пирамиданың, қиық пирамиданың жазбасы, бүйір беті және толық бетінің аудандары |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.3.2 - пирамиданың (қиық пирамиданың) бүйір және толық бетінің аудандары формулаларын қорытып шығару және оларды есептер шығаруда қолдану; 11.1.11 - көпжақтар мен айналу денелерінің жазбаларын жасай алу; |
|
Сабақтың мақсаты: |
- пирамиданың (қиық пирамиданың) бүйір және толық бетінің аудандары формулаларын қорытып шығарады және оларды есептер шығаруда қолданады; - көпжақтар мен айналу денелерінің жазбаларын жасай алады; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|
Сабақтың басы 5мин |
Ұйымдастыру кезеңі. Оқушылардың сабаққа дайындығын тексеру. Үй тапсырмасын тексеру. Өзіңді тексер! Пирамида жайлы түсініктерін бағалау мақсатында жеке жұмыс. Бағалау: Тапсырманы орындап болған соң оқушылар өзара жауаптарын тексеріп бағалайды, соңында қорытынды жасау. Мұғалімнің кері байланысы. |
Сәлемдеседі Үй тапсырмасын көрсетеді Сабақтың мақсатымен танысады |
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
|
|
Сабақтың ортасы 15мин |
Топтық жұмыс
Жалпы сыныптық жұмыс.
Проблемалық жағдаят тудыру. Оқушыларды топтастырып, төртбұрышты пирамида және төртбұрышты қиық пирамида пішіндес қораптағы сыйлықты тыстау үшін қанша түсті қағаз керек екенін есептеңіз. Қорытындыларды жалпылаңыз және дәптерлерде сәйкес жазуларды орындаңыз. Бүгінгі сабақ тақырыбы мен мақсатын анықтау. Бағалау критерийлері оқушылармен бірге талқыланады. Күтілетін нәтижелерге тоқталу.
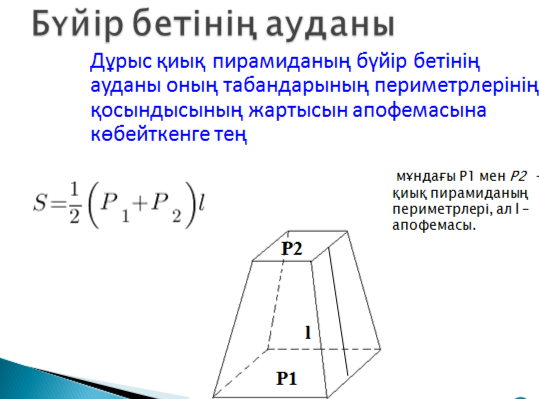
Қөпжақтардың табаны, бүйір және толық беттерінің аудыны түсініктерін енгізу. Пирамиданың және қиық пиарамиданың бүйір бетінің ауданын табу формуласын оқушыларға жұптасып, қорытып шығаруды ұсыныңыз. Дұрыс пирамиданың және дұрыс қиық пирамиданың бүйір бетінің және толық бетінің аудандарын қорытып шығарту. |
Пирамиданың толық бетінің ауданы – оның табаны мен бүйір бетінің аудандарының қосындысы. Sт.б.= Sт.+ Sб.б.
Дұрыс қиық пирамиданың бүйір беті оның табандарының периметрлерінің қосындысының жартысын апофемасына көбейткенге тең. Sб.б.=1/2(Р+Р1)к
P – табанының периметрі, l – апофема, h – пирамиданың биіктігі
|
Мұғалім жаңа тақырыпты түсіндіру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! ҚБ: «Екі жұлдыз, бір ұсыныс» бойынша мұғалімнің бағалауы |
ДК экраны Сұрақтар топтамасы. Оқулық 11-сынып.
|
|
Бекіту тапсырмалары 20мин |
|
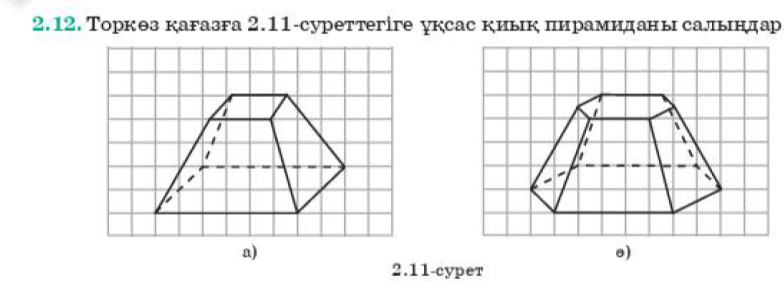
Оқулықтағы тапсырмаларды орындайды. Қиық пирамида салуды үйренеді
|
|
|
|
|
№1 Дұрыс төртбұрышты қиық пирамиданың табандарының қабырғалары 3 және 7 см-ге, ал бүйір жақтың сүйір бұрышы 450-қа тең. Пирамиданың толық бетін есептеңіз. |
Тапсырманы орындайды Жауабы: Sт.б. = 98 см2. |
Дескрипторлар: есептің шарты бойынша сызбаны салады; -пирамида апофемасының ұзындығын табады -пирамиданың бүйір бетінің ауданын есептейді; пирамиданың толық бетінің ауданын есептейді |
|
|
|
№2 Дұрыс үшбұрышты қиық пирамиданың табандарының биіктіктері 6 және 9 см-ге, ал табанындағы екіжақты бұрышы 600-қа тең. Пирамиданың толық бетін есептеңіз. №3. Дұрыс үшбұрышты қиық пирамиданың табандарының қабырғалары 3 және 6 см-ге тең. Пирамиданың бүйір қыры табан жазықтығына 600 бұрышпен көлбеленген. Пирамиданың толық бетін есептеңіз. Жауабы: Sт.б. = |
Жауабы: Sт.б. =
69
№3Дескрипторлар:
|
Дескрипторлар: -есептің шарты бойынша сызбаны салады; -үстінгі және төменгі табандарына іштей сызылған шеңберлердің радиустарын табады; -пирамида апофемасының ұзындығын табады; -пирамиданың бүйір бетінің ауданын есептейді; пирамиданың толық бетінің ауданын есептейді |
|
|
|
Тест тапсырмалары: 1. Пирамида төбесін табан қабырғасының төбелерімен қосатын кесінді А) пирамида осі В) апофема С) бүйір қырлары 2. Табанында үшбұрыш жатқан пирамида А) октаэдр В) тетраэдр С) төртбұрышты пирамида 3. Табанында дұрыс n көпбұрыш, бүйір қырлары өзара тең пирамида А) дұрыс В) қиық С) кез келген 4. Бүйір бетінің ауданы А) бүйір жақтарының В) бүйір қырларының С) барлық жақтарының аудандарының қосындысына тең 5. Апофема деп ... А) табанының В) бүйір жағының С) кез келген қырына түсірілген биіктік |
6. Төртбұрышты пирамиданың неше жағы бар? А) 4 В) 5 С) 6 7. Тетраэдрда неше қыр бар? А) 6 В) 7 С) 8 8. Дұрыс үшбұрышты пирамиданың табан қабырғасы а, бүйір қыры в, биіктігі неге тең? А) √в2-3а2 В) √в2-а2/3 С) √3в2-а2 9. Төртбұрышты пирамиданың неше диагональдың қимасы болады А) 4 В) 2 С) 1 10. Дұрыс пирамиданың толық бетінің ауданы неге тең? А) S=Ph+Sт В) S=Pl/2+Sт С) S=Pl+Sт |
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл Әрбір дұрыс жауапка 1 балл қойылады |
|
|
Сабақтың соңы |
Саралау: Бұл кезеңде саралаудың «Қорытынды» тәсілі көрінеді. Үйге тапсырма: № |
|
1-10 баллдық жүйе бойынша оқушылардың сабаққа қатысу белсенділігі бойынша бағаланады. |
Жұмыс дәптерлері. Слайд.
Білім поштасы, хаттар |
|
Ұзақ мерзімді жоспар бөлімі: |
Көпжақтар |
|
Педагогтің Аты,Тегі, Әкесінің аты |
Абдуллаева Д |
|
Күні: |
07/11/24 |
|
Сыныбы: 11ә |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Пирамиданың, қиық пирамиданың жазбасы, бүйір беті және толық бетінің аудандары |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.3.2 - пирамиданың (қиық пирамиданың) бүйір және толық бетінің аудандары формулаларын қорытып шығару және оларды есептер шығаруда қолдану; 11.1.11 - көпжақтар мен айналу денелерінің жазбаларын жасай алу; |
|
Сабақтың мақсаты: |
- пирамиданың (қиық пирамиданың) бүйір және толық бетінің аудандары формулаларын қорытып шығарады және оларды есептер шығаруда қолдану; - көпжақтар мен айналу денелерінің жазбаларын жасай алу; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
||||||||||||||||||||||||||||||||||||
|
Сабақтың басы |
Теориялық материалды қайталау. Пирамиданың, қиық пирамиданың бүйір беті және толық бетінің аудандары. Кестенің оң жақтағы бағанын толтыруға ұсыну.
|
Үй тапсырмасын
тексеру:
-Пирамиданың табанының ауданын табады; -Пирамиданың бүйір жақтарының ауданын табады; -Пирамиданың толық бетінің ауданын табады.
Бағалау: Жұптасқан оқушылар бір-бірінің жұмысын дескрипторлар бойынша тексереді. Мұғалім оқушылар жұмысын бақылап кері байланыс береді.
|
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!»
|
Түрлі түсті қима қағаздар
|
||||||||||||||||||||||||||||||||||||
|
Сабақтың ортасы
|
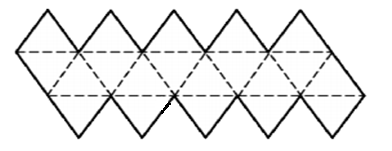
Оқушыларға сәйкестіруге есептер ұсыныңыз. Кестенің бірінші бағанында көпжар және айналу денелер көрсетілген, екінші бағанында олардың жазбалары. Көпжардың және айналу денелердің жазбаларын сәйкестіру керек. Дайын кесте арқылы тексеріс жүргізіңіз. Дұрыс көпжақтардың бес түрінің жазбасын қарастырыңыз.
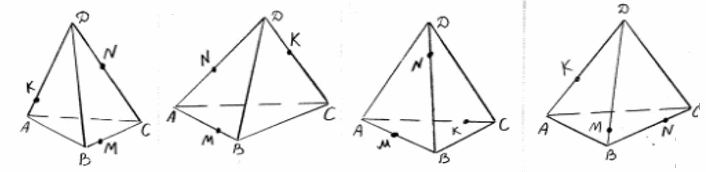
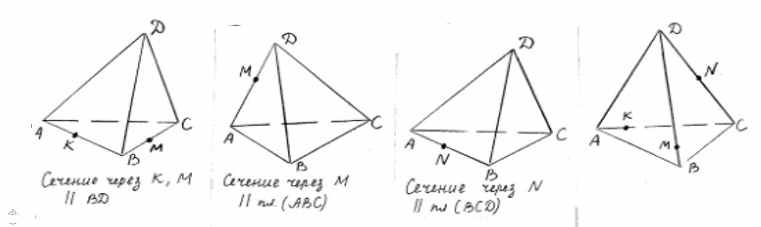
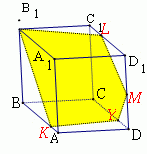
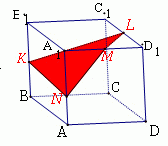
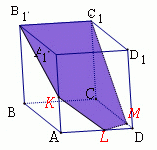
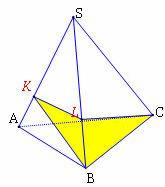
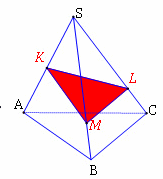
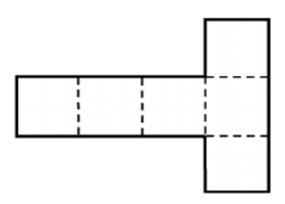
Оқушылар мен дұрыс көпжақтардың басқа жазбалары болуы мүмкін бе деген сұрақты талдаңдар. Жазбаның басқа түрлерін көрсетіңіз. Оқушыларға бекітуге арналған тапсырмаларды ұсыныңыз. 1. Суретте көрсетілген жазбалардың қайсысы пирамида жазбасы болады? Неғе? Пирамиданың қанша жазбасын көрсетуге болады ? 2. Суретте көрсетілген жазбалардың қайсысы призма жазбасы болады? Призманың қанша жазбасын көрсетуге болады ? Призмалар қандай?
(" Астаны геометриясы" кітабынан) 3.
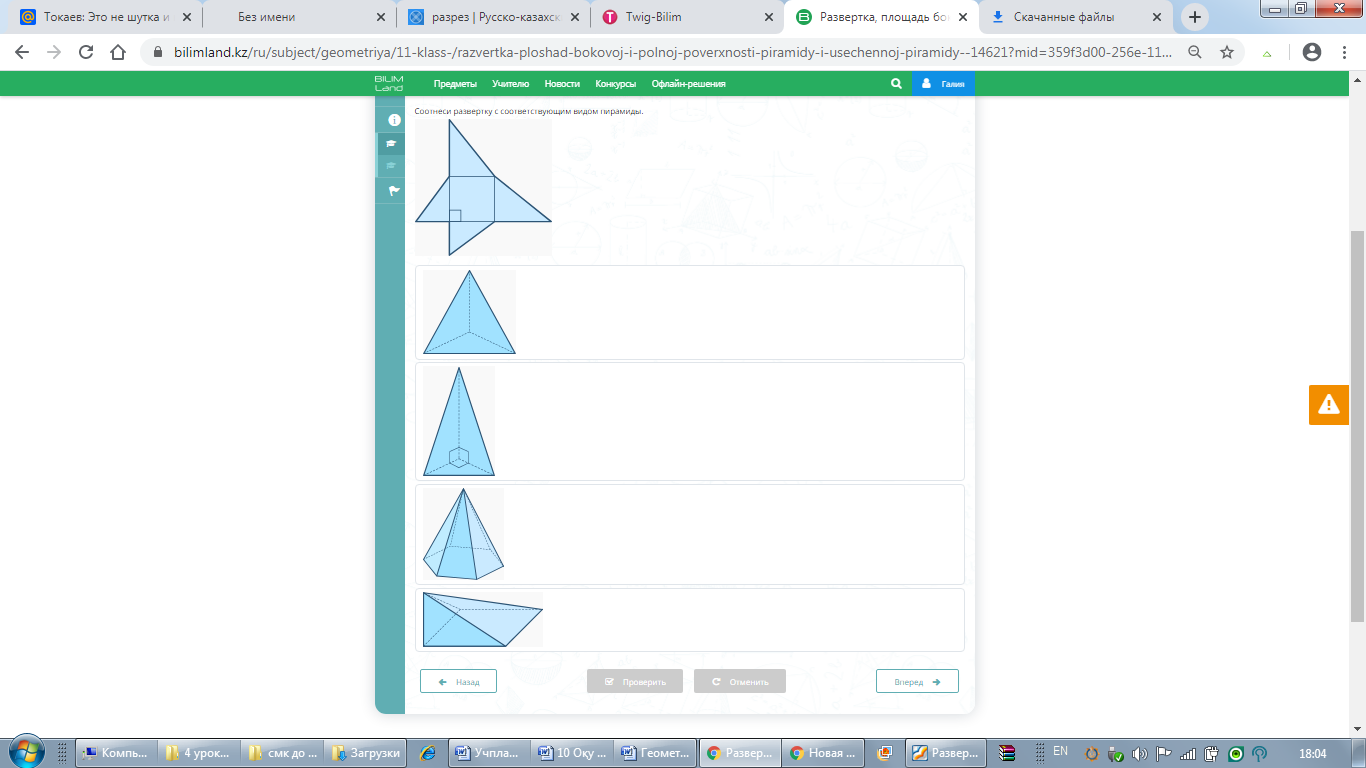
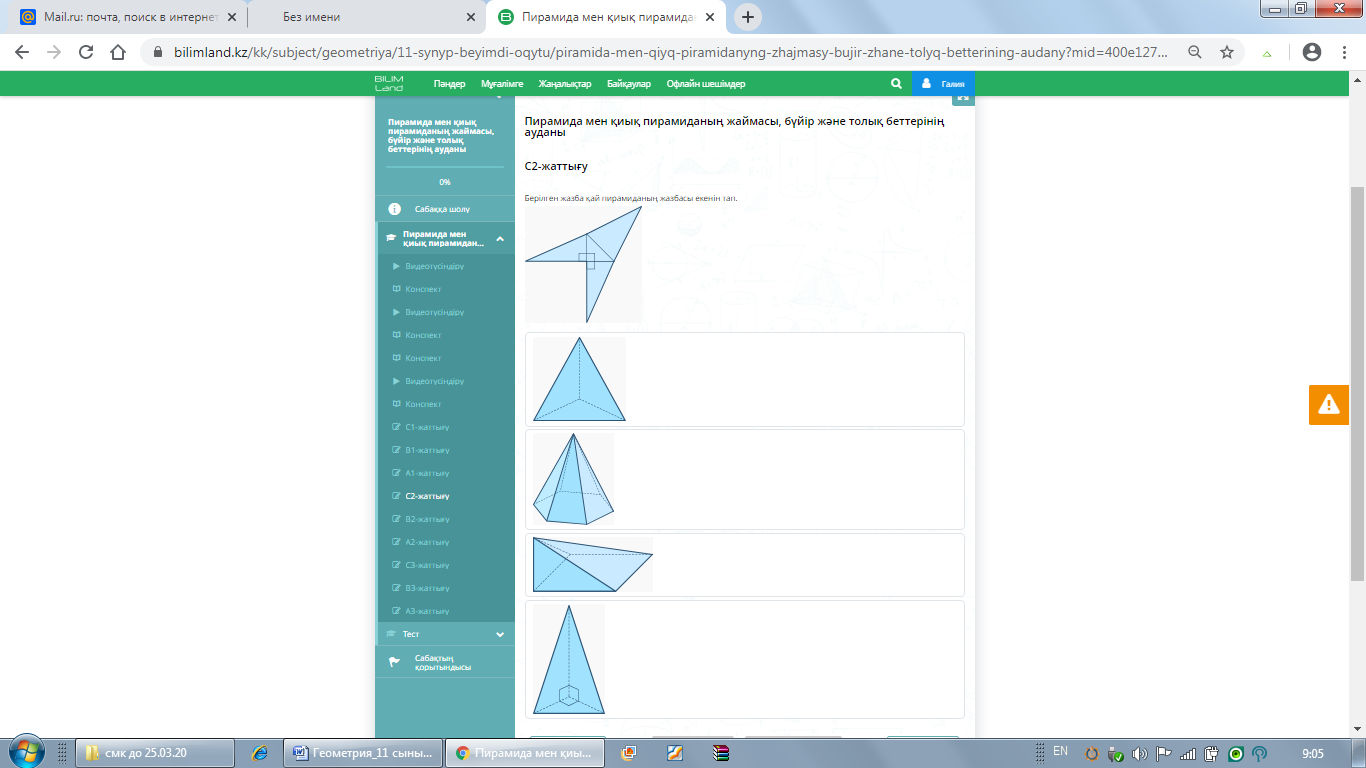
Жауабы: 2,3 сурет С1 Жазбаны пирамиданың түрімен сәйкестендіріңіз:
С2 Берілген жазба қай пирамиданың жазбасы екенін табыңыз.
|
Сыныпен жұмыс. Мақсаты: Пирамиданың сызықтық элементтерін және бұрыштарын қайталау.
Сөйлемді аяқтаңыз:
Бағалау дайын жауаптар арқылы жүргізіледі:
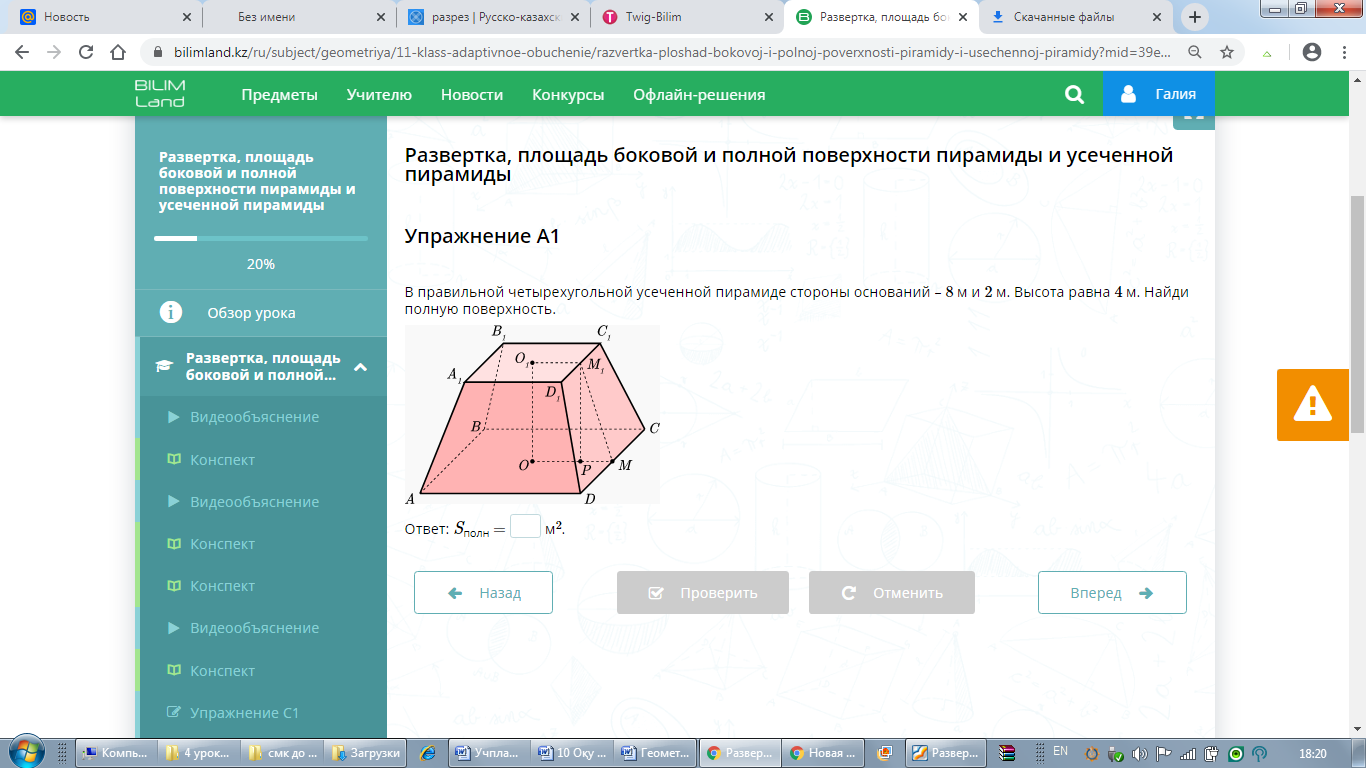
Деңгейлік тапсырмаларды орындау. Дифференциация: оқушылардың қабілеттеріне қарай материалды күрделендіру. Оқушыларға деңдейді қабілеттеріне қарай өздеріне таңдауға ұсыныс беріледі А1 Дұрыс төртбұрышты қиық пирамиданың табандары 8 м және 2 м. Биіктігі 4 м. Қиық пирамиданың толық бетін табыңыз
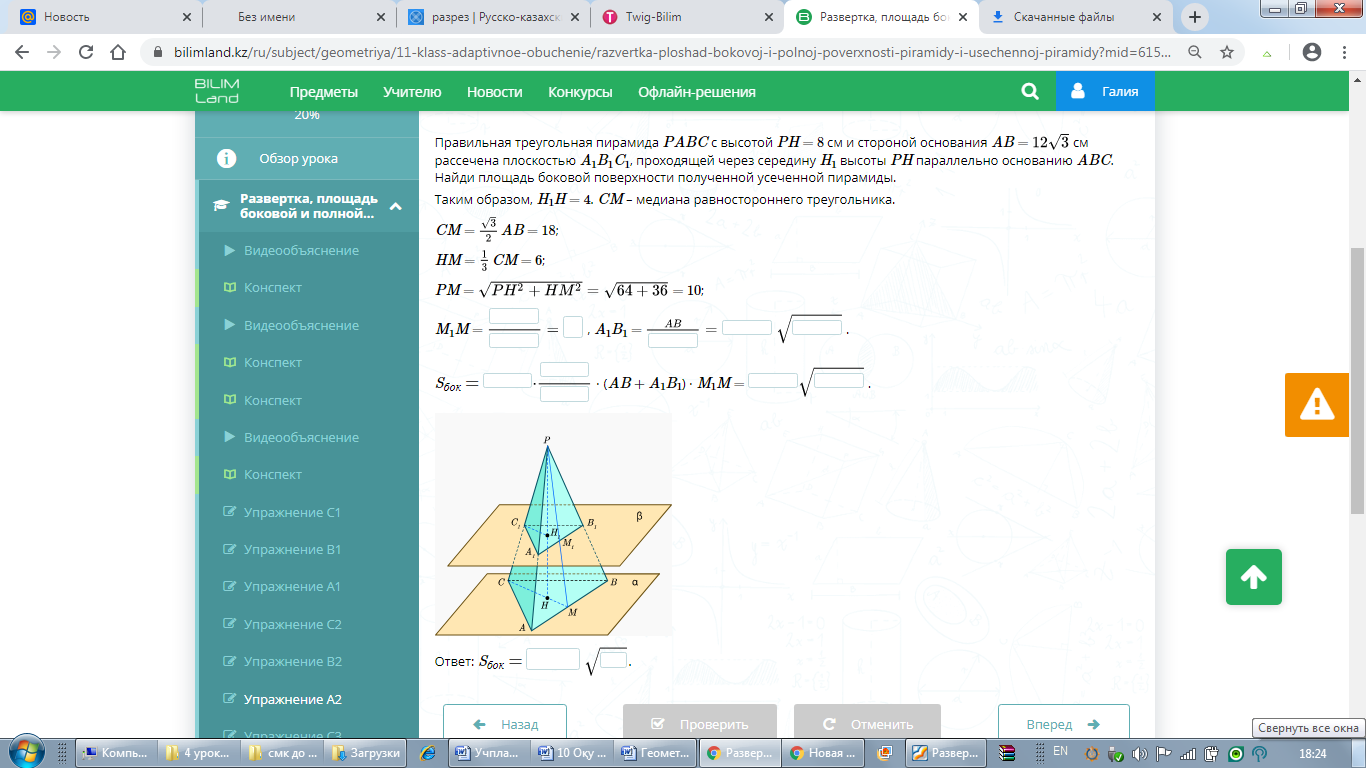
А2
PABC -
дұрыс үшбқрышты пирамида, Биіктігі
А3 Пирамиданың табанында қабырғасы 10 см-ге тең квадрат жатыр. Пирамида биіктігінің табаны оның табанының бір төбесі болып табылады. Егер оның биіктігі 24 см-ге тең болса, пирамиданың толық бетінің ауданын табыңыз.
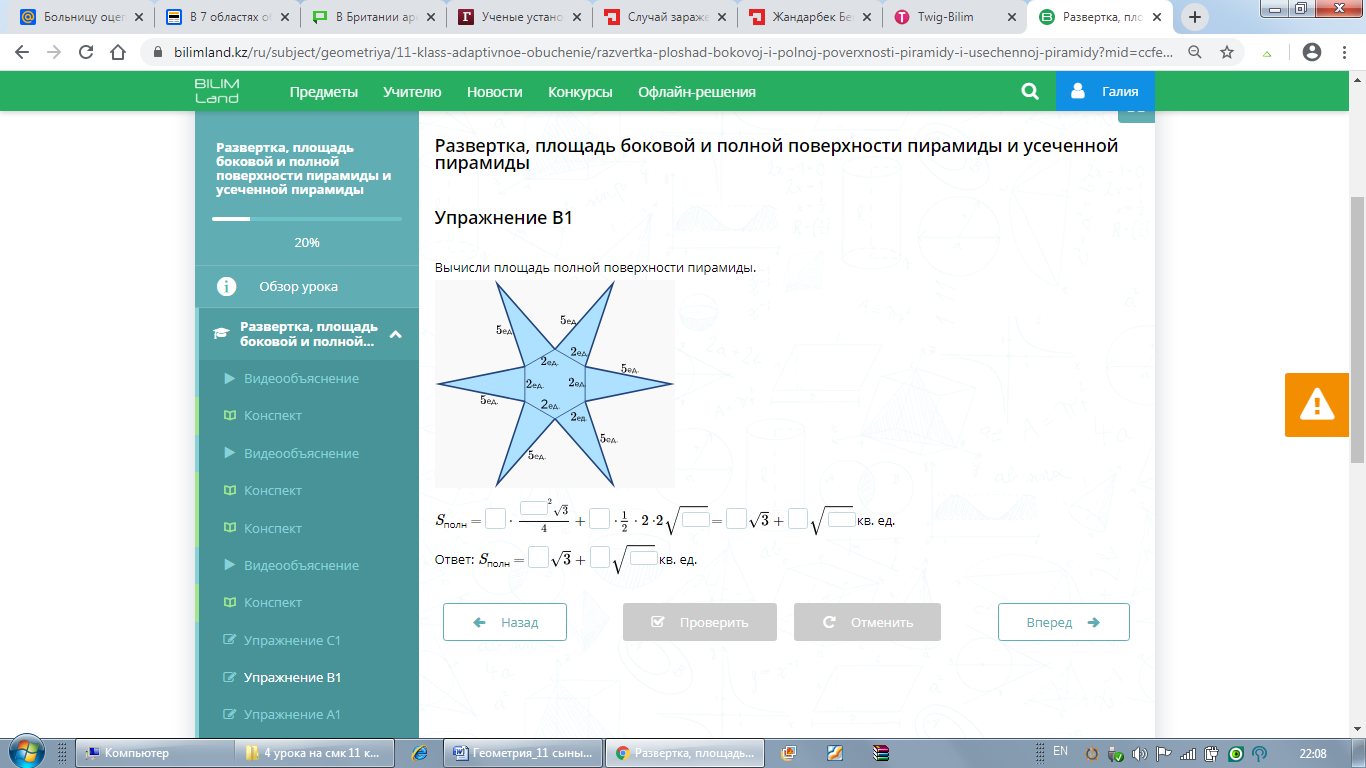
B1
Пирамиданың толық бетінің
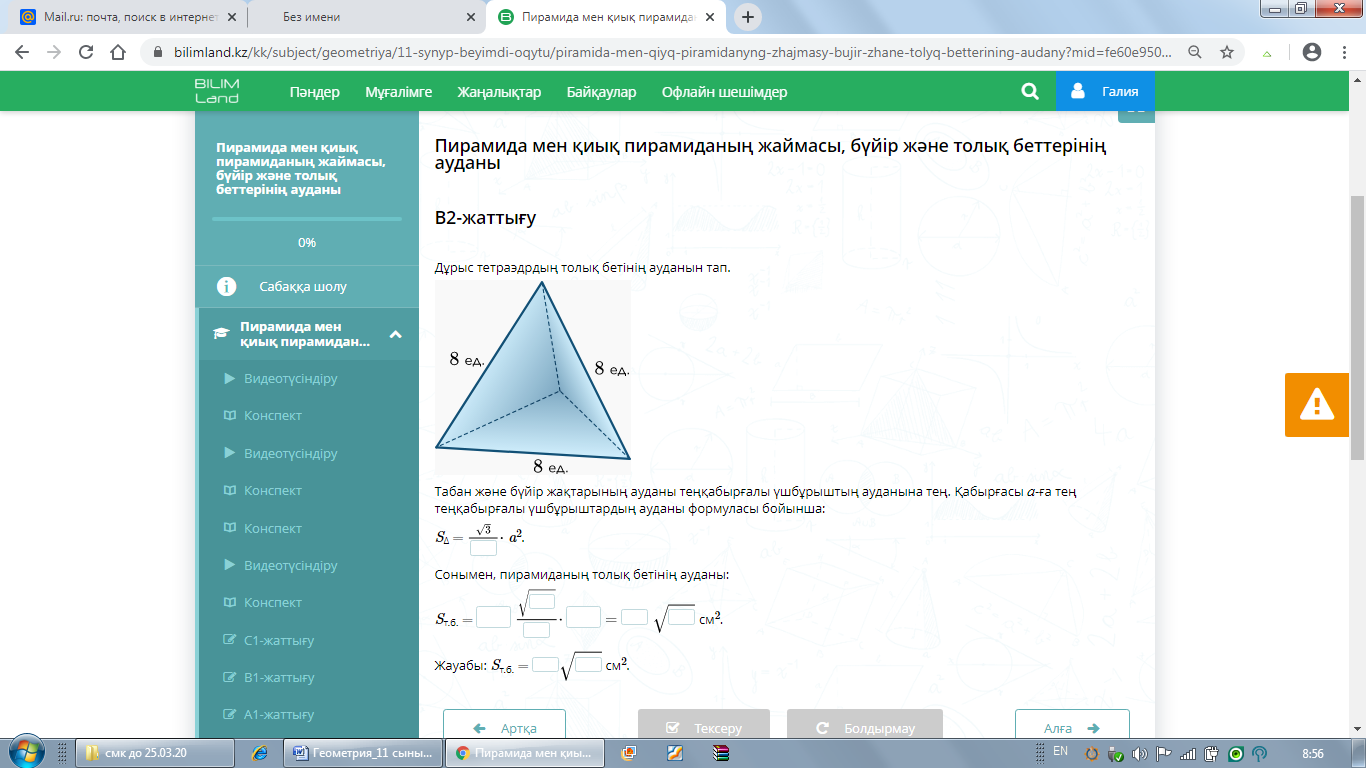
ауданын табыңыз: В2 Дұрыс тетраэдрдың толық бетінің ауданын табыңыз:
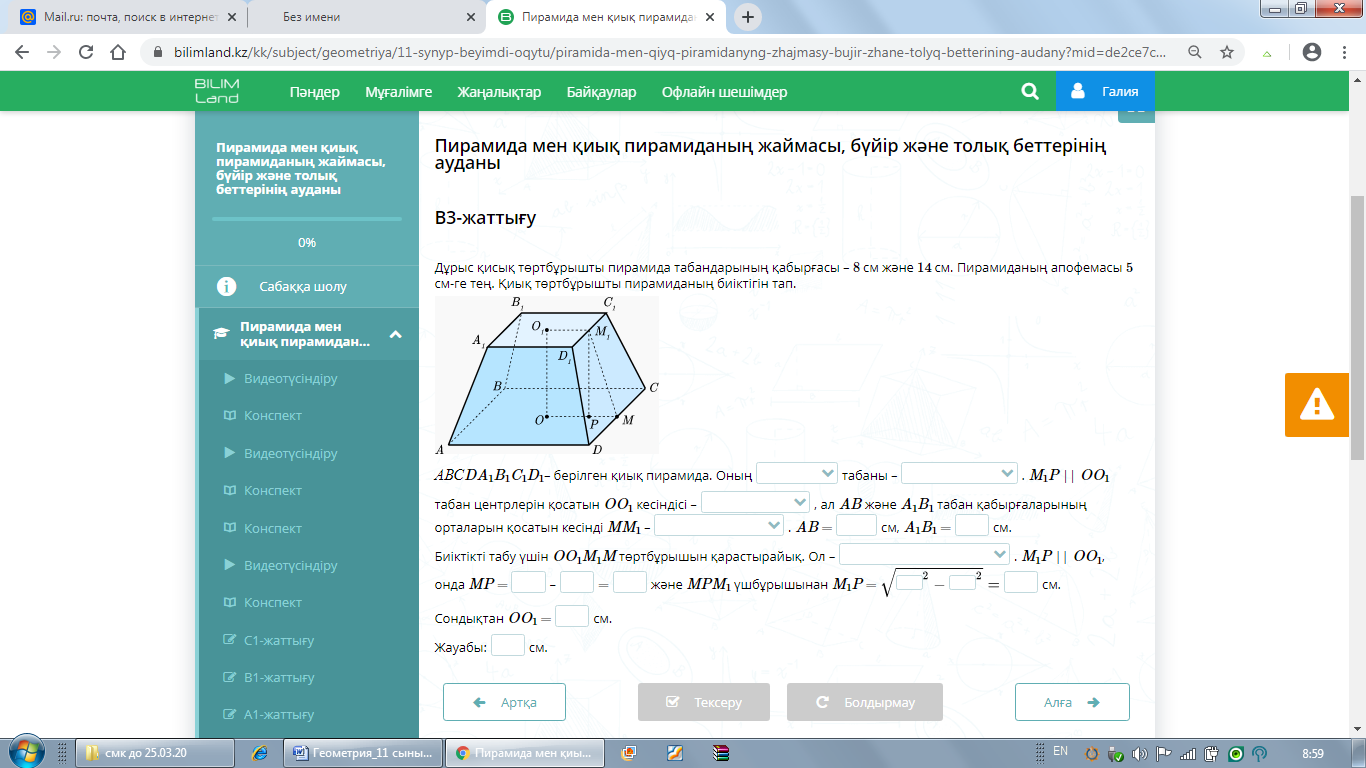
В3 Дұрыс қиық төртбұрышты пирамида табандарының қабырғалары – 8 см және 14 см. Пирамиданың апофемасы 5 см-ге тең.Қиық төртбұрышты пирамиданың биіктігін табыңыз.
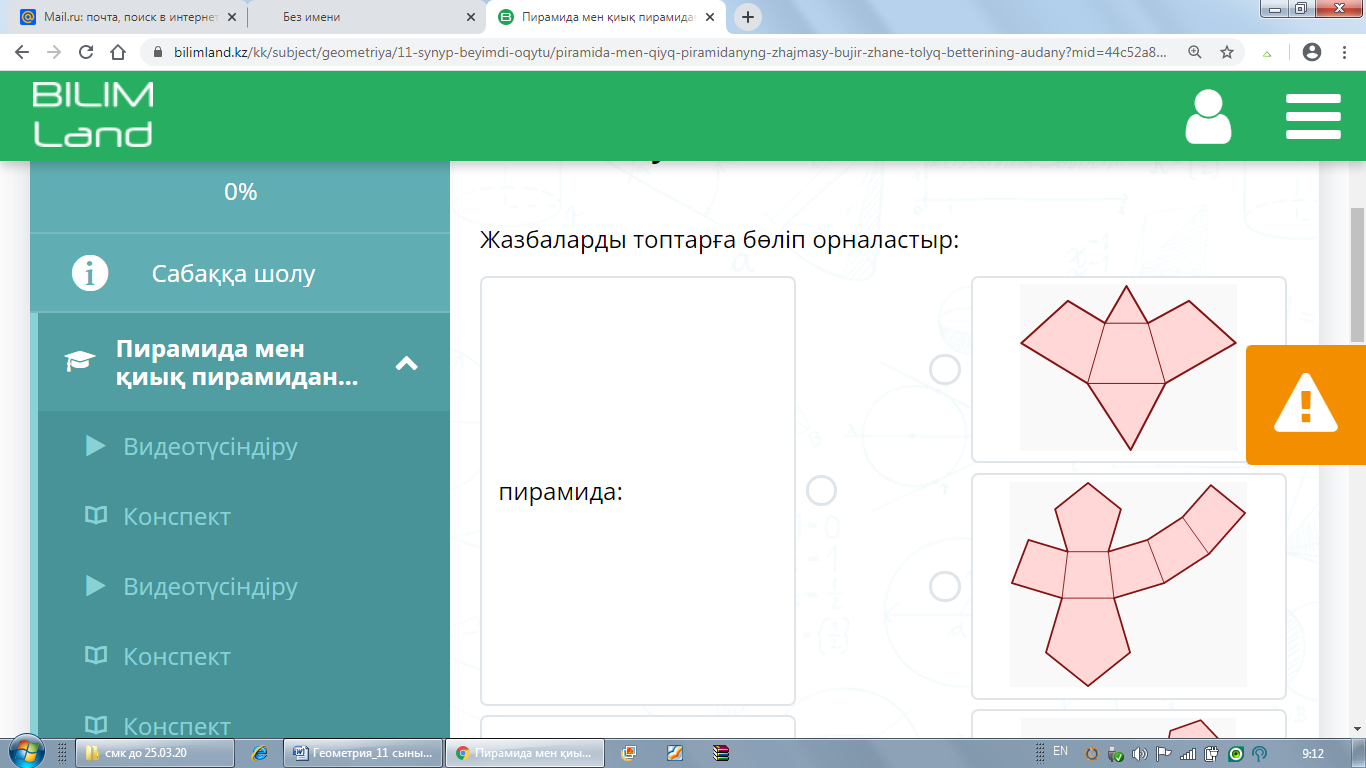
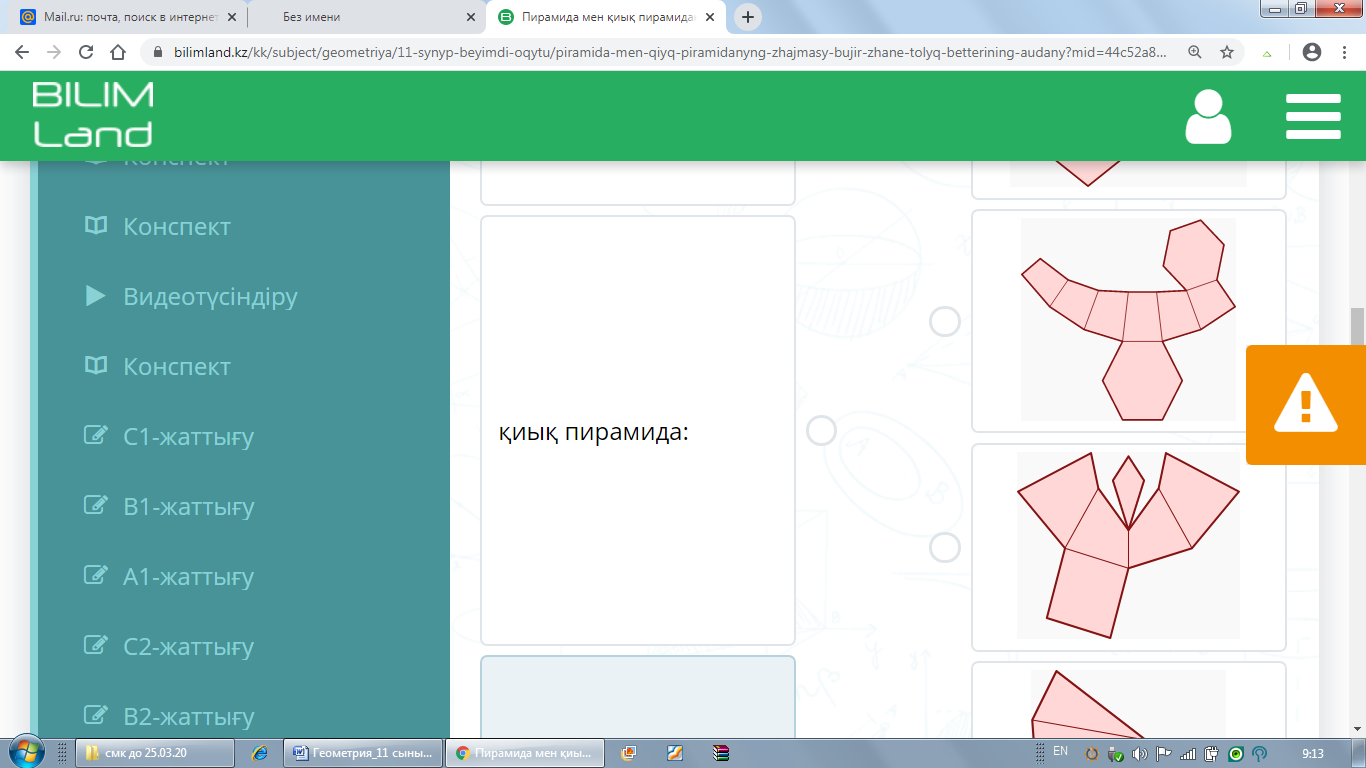
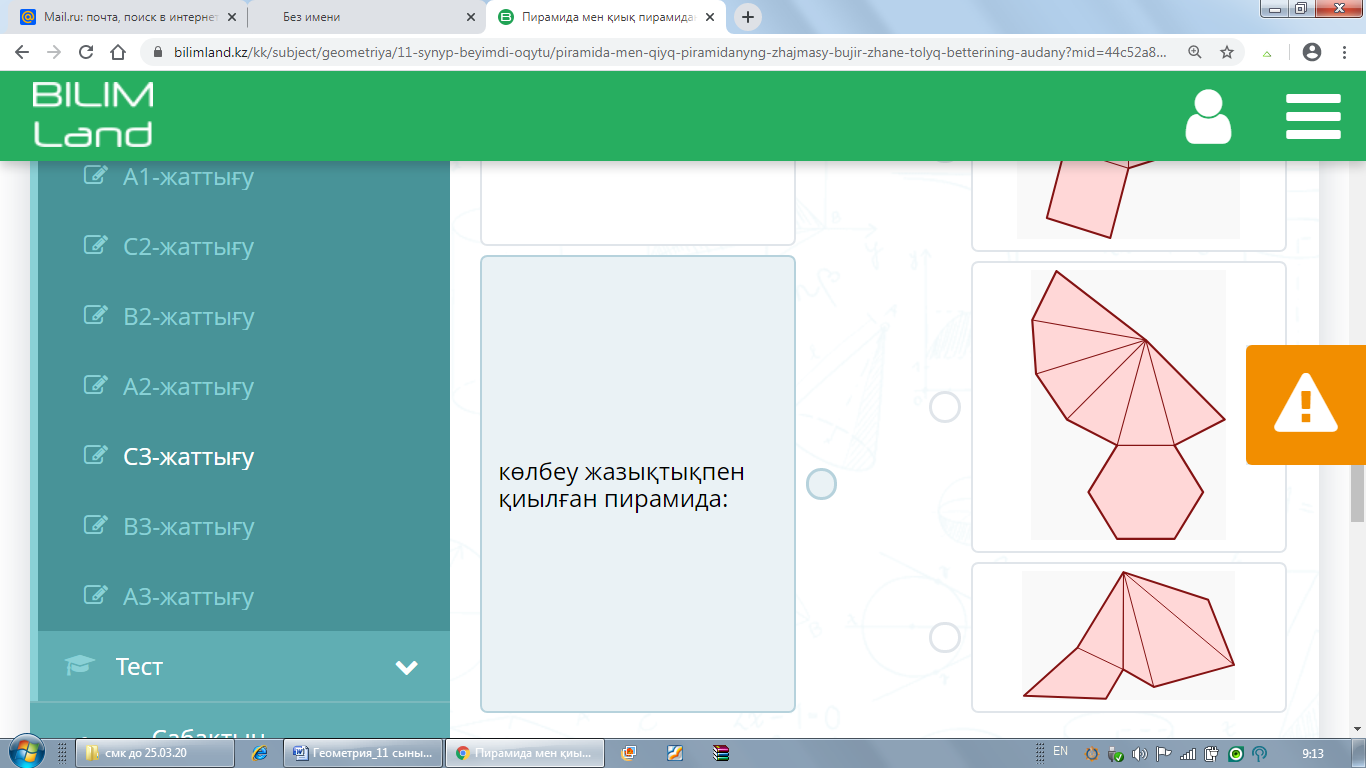
С1 С3 Жазбаларды топтарға бөліп орналастырыңыз: пирамида, қиық пирамида, көлбеу жазықтықпен қиылған пирамида.
Қосымша материал. (Деңгейлік тапсырмалардың орнына жеке жұмысты орындауға болады) Бағалау критерийлері:
Жауабын жазады
|
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл
Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны
Сұрақтар топтамасы.
Оқулық 11-сынып.
|
||||||||||||||||||||||||||||||||||||
|
Сабақтың соңы |
Сабақ соңында оқушылар рефлексия жүргізеді: - нені білдім, нені үйрендім - нені толық түсінбедім - немен жұмысты жалғастыру қажет Оқушылар өздерінің жұмысы мен сыныптастарының жұмысын белгілі бір критерийлер бойынша бағалайды
|
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. - Кейбір оқушыларға мұғалім тарапынан кері байланыс беріледі.
|
|
||||||||||||||||||||||||||||||||||||
Тексерілді:
|
Ұзақ мерзімді жоспар бөлімі: |
Көпжақтар |
|
|
Педагогтің Аты,Тегі, Әкесінің аты |
Абдуллаева Д |
|
|
Күні: |
12/11/24 |
|
|
Сыныбы: 11ә |
Қатысушылар саны: Қатыспағандар саны: |
|
|
Сабақтың тақырыбы: |
Көпжақтардың жазықтықпен қималары |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.2.1 - көпжақтың жазықтық пен қималарын сала білу; |
|
|
Сабақтың мақсаты: |
- көпжақтың жазықтық пен қималарын сала біледі; |
|
|
Құндылықтарды дарыту |
«Жалпыға бірдей еңбек қоғамы» құндылығына: Топпен, жұппен жұмыс орындау барысында құрмет, серіктестік және жеке жұмыс орындау кезінде жауапкершілік, үздіксіз оқу құндылықтарын дарыту. |
|
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|||||||||
|
Сабақтың басы |
Аксиомаларды және олардың салдарларын қайталау.
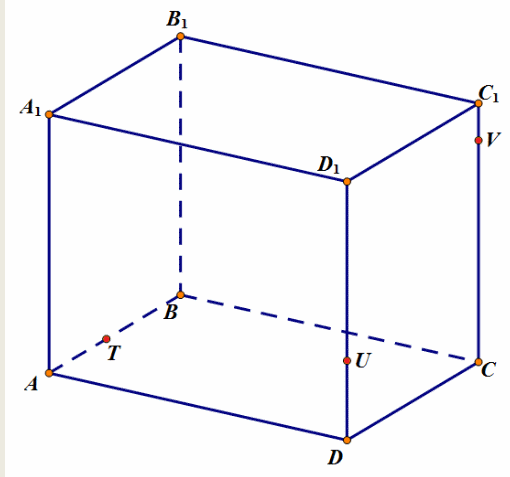
Салу керек: 1.EFтүзу мен АВС жазықтықтың қиылысу нүктесін; 2.DK түзу мен ЕFM жазықтықтың қиылысу нүктесін. 3. DBK және АСD жазықтықтардың қиылысу түзуін 4. EFM және АСD жазықтықтардың қиылысу түзуін |
Көпжақтардың анықтамаларын еске түсіру
Суреттерге теоремалар мен қасиеттерді тұжырымдау.
Оқушылар жүппен жұмыс жасайды. Бір-біріне ретімен ұсынылған сұрақтар қояды. Қандай қөпжақ параллелепипед деп аталады? Ол қандай қасиеттерге ие болады? Қандай жазықтық қиюшы деп аталады? Қимад не болады? Қиманы салудағы негізгі ережелерін айтып беріңіз. Үй жұмысын тексеру. |
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
Түрлі түсті қима қағаздар
|
|||||||||
|
Сабақтың ортасы |
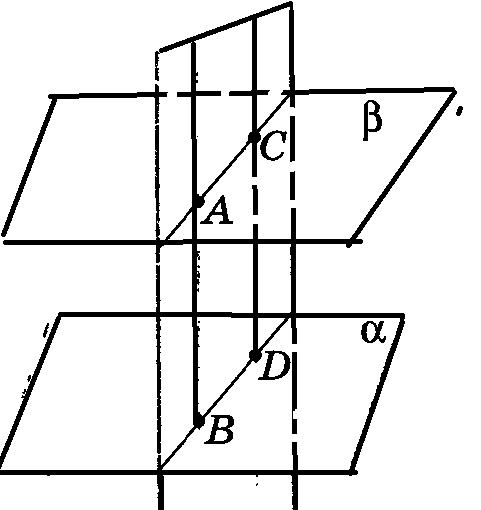
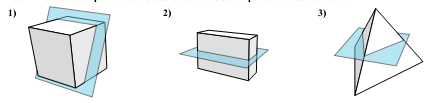
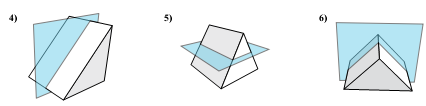
. Жаңа тақырыпты меңгеру. Берілген денені жазықтық екі денеге бөлетіні белгілі. Егер дененің α жазықтығымен шектелетін екі жарты кеңістікке де тиісті нүктелері бар болса, онда α-ны денені қиюшы жазықтық деп атайды. Ал дене мен жазықтықтың қиылысуынан пайда болған фигураны қима деп атайды. Көпжақтың қимасын жазықтық арқылы тұрғызу дегеніміз – қиюшы жазықтықтың көпжақтың қырларымен қиылысатын нүктелерін белгілеп, сол нүктелерді көпжақ қырларына тиісті кесінділер арқылы байланыстыру. Қиюшы жазықтық – берілген дене мен қима жазықтық үшін ортақ болатын нүктелер жиыны.
Көпжаққа қима тұрғызу ережелері. 1) бір жазықтықта жататын нүктелер арқылы түзулер жүргіземіз; 2) қима жазықтығы мен көпжақ қырларының қиылысу түзулерін іздейміз, ол үшін: a) қима жазықтығына тиісті түзу мен бір жазықтықта жататын қырлардың біреуіне тиісті түзумен қиылысу нүктелерін іздейміз; b) көпжақтың параллель жақтарын қима жазықтығы параллель түзулердің бойымен қияды. Материалды бекіту үшін сұрақтар:
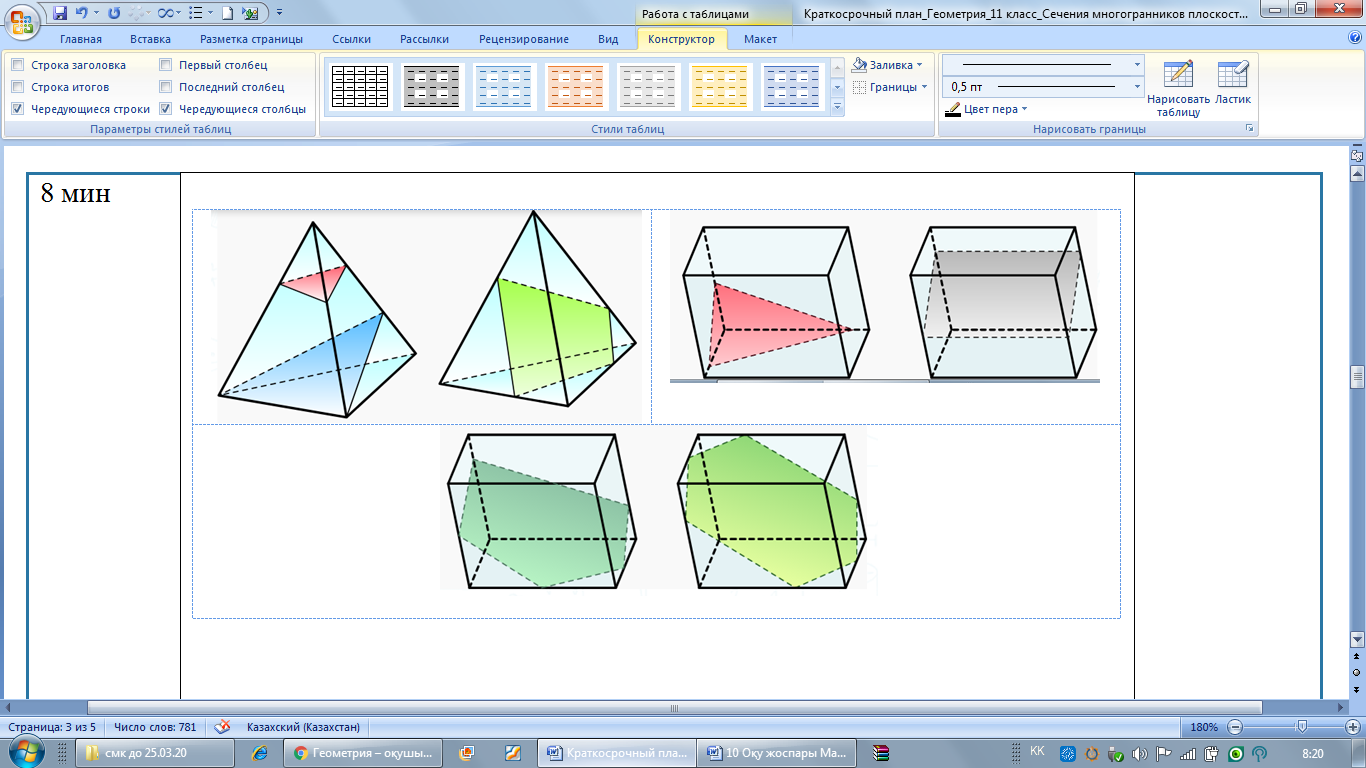
Суреттерге сұрақтар құрастырыңыз. Қай суретте қима қате салынған? (8-слайд)
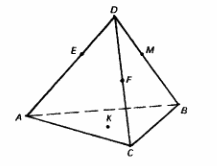
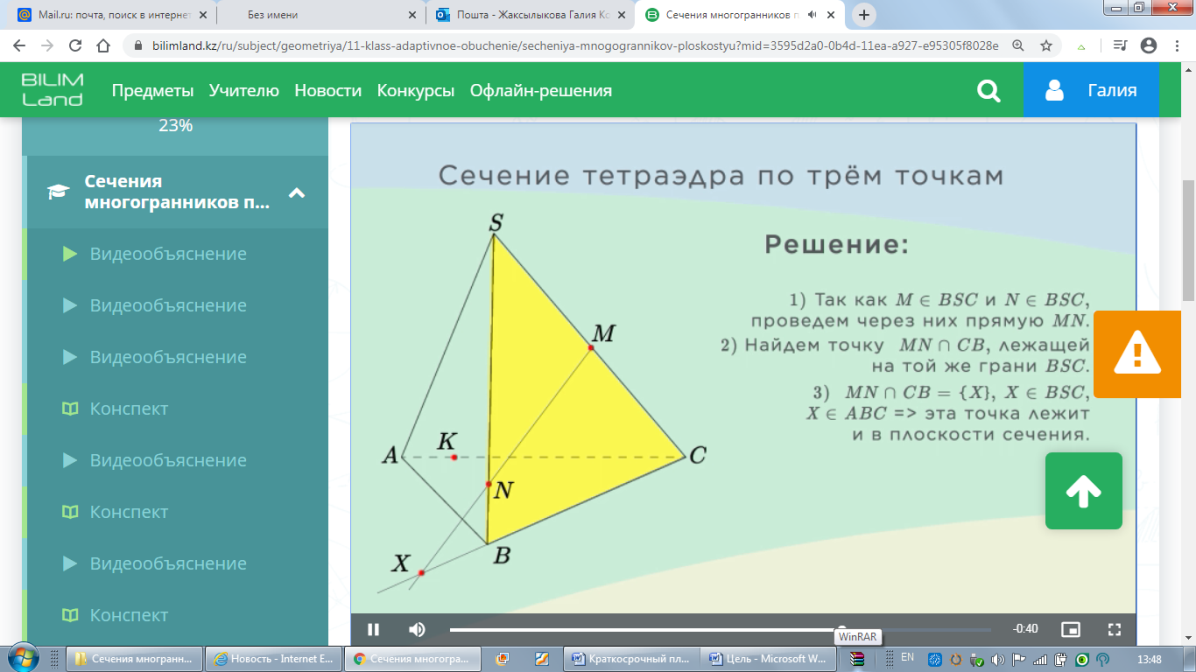
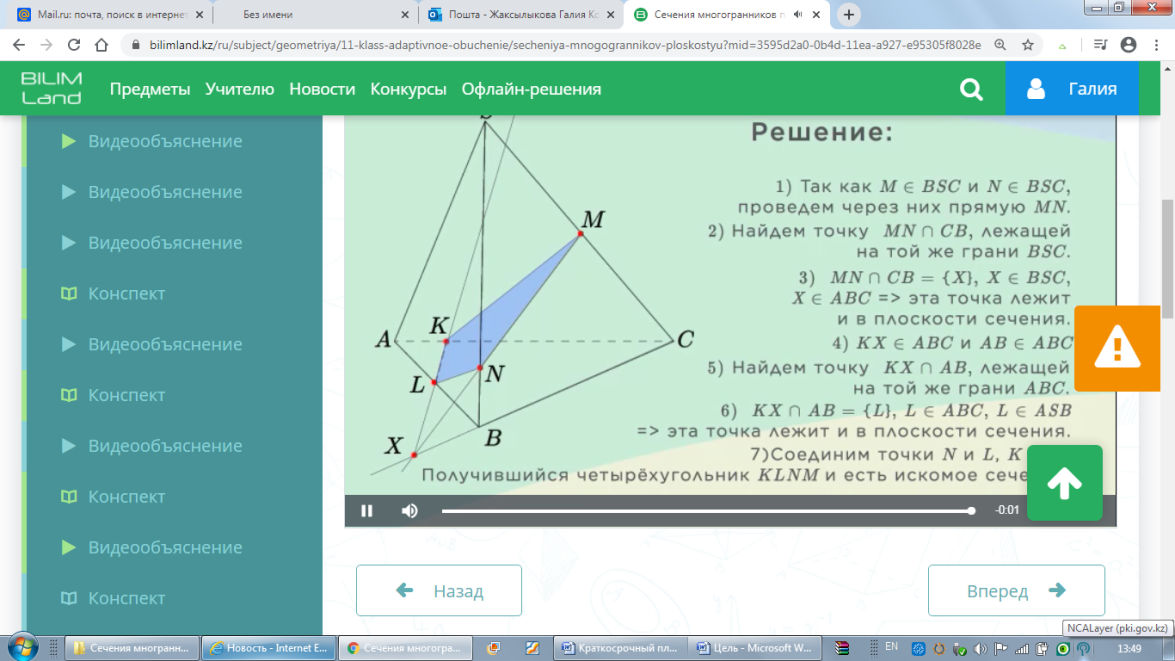
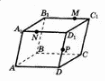
Тетраэдрдың қимасын салу
Үш нүкте арқылы тетраэдрдың қимасын салу
|
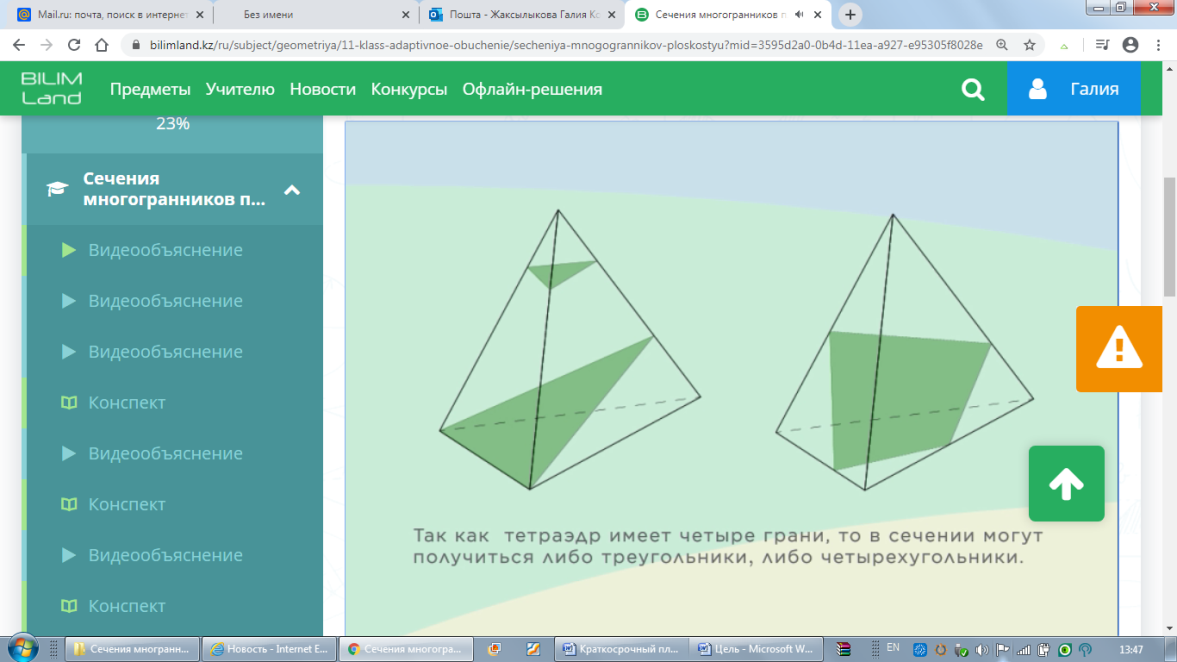
Көпжақтарды қарастырайық. Осы суреттерде не ортақ? (әрбір көпжақтың ішіндегі көпбұрыштар) Сабақтың тақырыбын тұжырымдау. Осы тақырыптың маңыздылығы туралы айту (презентация) Қиюшы жазықтықтың анықтамасын беру. Көпжақтың қиюшы жазықтығы деп оның екі жағында берілген көпжақтың нүктелері бар болатын кез келген жазықтықты айтады. Қиюшы жазықтық көпжақтың жақтарын кесінді мен қияды, осы кесінділер қабырғасы болатын көпбұрыш көпжақтың қимасы деп аталады. Анықтамаға сүйеніп, қай суретте қима сызылғанын айтыңдар?
Қиманы салу үшін ережелерді тұжырымдайық:
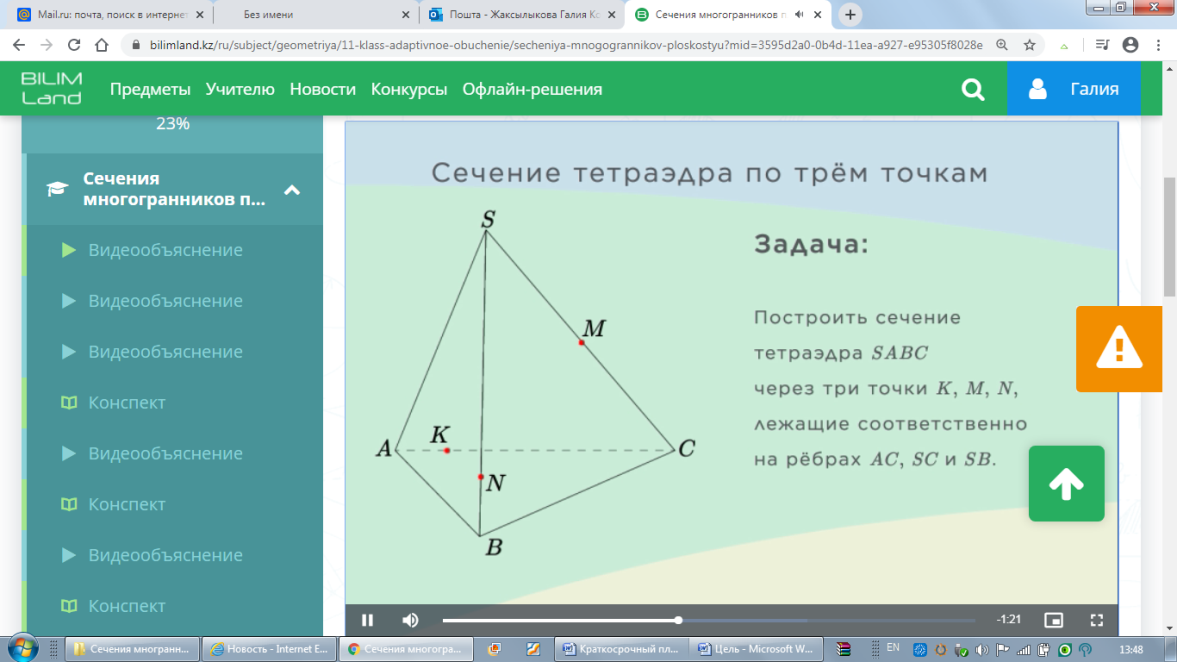
Сабағымыздың мақсаты: тетраэдрдің қимасын салу. Қандай фигураны тетраэдр дейді? Оның қанша жағы бар? Қимасында қандай көпбұрыштар пайда бола алады? Неге? Қиманы салу үшін қанша нүкте беру керек? Топпен шығармашылық жұмыс: тетраэдрды салу. Қимасында үшбұрыш, төртбұрыш болатындай етіп, тетраэдрдың қырларында нүктелер беру. Мұғалімнің байқауында жеке жұмыс жасау. Тексеруді GeoGebra арқылы жасауға болады. Тетраэдрдың қимасын берілген нүктелер бойынша салу.
|
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл
Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны
Сұрақтар топтамасы.
Оқулық 11-сынып.
|
|||||||||
|
Сабақтың соңы |
қимасын салыңыз,
мұнда DМ=МВ.
|
Ауызша жұмыс. Активити. Көпжақты жазықтықпен қиғанда пайда болған фигураны анықтаңыз:
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. - Кейбір оқушыларға мұғалім тарапынан кері байланыс беріледі.
|
|
|||||||||
Тексерілді:
|
Ұзақ мерзімді жоспар бөлімі: |
Көпжақтар |
|||
|
Педагогтің Аты,Тегі, Әкесінің аты |
Абдуллаева Д |
|||
|
Күні: |
14.11.24 |
|||
|
Сыныбы: 11ә |
Қатысушылар саны: Қатыспағандар саны: |
|||
|
Сабақтың тақырыбы: |
Көпжақтардың жазықтық пен қималары |
|||
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.2.1 - көпжақтың жазықтық пен қималарын сала білу; |
|||
|
Сабақтың мақсаты: |
- көпжақтың жазықтық пен қималарын сала біледі; |
|||
|
Құндылықтарды дарыту |
«Жалпыға бірдей еңбек қоғамы» құндылығына: Топпен, жұппен жұмыс орындау барысында құрмет, серіктестік және жеке жұмыс орындау кезінде жауапкершілік, үздіксіз оқу құндылықтарын дарыту. |
|
|
|
Сабақтың барысы:
Қысқа мерзімді жоспар №5-сабак
|
Ұзақ мерзімді жоспар бөлімі: Көпжақтар |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Дұрыс көпжақтар |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.1.6 - дұрыс көпжақтың анықтамасын білу, дұрыс көпжақтардың түрлерін ажырата білу; |
|
Сабақтың мақсаты: |
- дұрыс көпжақтың анықтамасын білу, дұрыс көпжақтардың түрлерін ажырата біледі; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Сабақтың басы |
Ұйымдастыру кезеңі: - оқушылардың назарын шоғырландыру; - оқушылармен бірге оқу мақсатын анықтау - оқушылардың «жақын арадағы дамуын» анықтау. Үй тапсырмасын тексеру. |
Геометриялық денелердің модельдерімен жұмыс жасау. Денелердің жиынтығына тетраэдрдің, октаэдрдің, кубтың, икосаэдрдің, додекаэдрдің, цилиндрдің, конустың, төртбұрышты пирамиданың, қиық пирамиданың, алтыбұрышты призманың, көлбеу параллелепипедтің және дөңес емес көпжақтардың модельдері кіреді. Тапсырма. Сіздердің алдарыңызда геометриялық денелердің модельдері жатыр. Көпжаққа жатпайтын модельдерді бөлек қойыңыздар. Көпжақтар дегеніміз не? Дөңес емес көпжақтардың модельдерін алып тастаңыздар. Қандай көпжақтар дөңес деп аталады? Қалған көпжақтарды қалай классификациялауға болады? (призмалар мен пирамидалар) Призмалар мен пирамидалардың ішінен дұрыс призма мен дұрыс пирамидаларды таңдап алыңыздар. Қандай призма дұрыс призма деп аталады? Қандай пирамида дұрыс пирамида деп аталады? |
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
Түрлі түсті қима қағаздар
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Сабақтың ортасы |
Жаңа материалды меңгеру. Видеофильмді көру. www.youtube.com/watch?v=KXm3xUGkLjw Анықтама. Егер дөңес көпжақтың жақтары қабырғаларының саны бірдей дұрыс көпбұрыштар болса және көпжақтың әрбір төбесінен шығатын қырларының саны бірдей болса, онда оны дұрыс көпжақ деп атайды. –Сіздер қандай көпжақтыларментаңыссыздар? (тетраэдр, куб) Дұрыс көпжақтардың 5 түрі бар: дұрыс тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр. Дұрыс тетраэдр – дұрыс үшбұрыштан құралған: әрбір төбесінде үш қыры тоғысады. Куб – алты квадраттан құралған: әрбір төбесінде үш қыры тоғысады. Куб – жақтары тең тікбқрышты параллелепипед. Октаэдр – сегіз дұрыс үшбұрыштан құралған: әрбір төбесінде төрт қыры тоғысады. Додекаэдр – дұрыс бесбұрыштан құралған: әрбір төбесінде үш қыры тоғысады. Икосаэдр – жиырма дұрыс үшбұрыштан құралған: әрбір төбесінде бес қабырғадан тоғысады. Историялық материалы. Дұрыс көпжақтардың қасиеттері туралы ең алғаш рет грек ғалымы Платон тапты. Сондықтан дұрыс көпжақтар «Платон денелері» деп аталады. ІІІ. Кесте толтыру. Тапсырма 1.Оқушылар кестені толтырады және жауаптарымен тексереді. Дұрыс көпжақтардың негізгі элементтері.
Кестені толтырып, оны Эйлер теоремасымен (формуласымен) тексереді. Т + Ж = Қ + 2, мұндағыҚ – қырлар саны, Т – төбелер, Ж–жақтар.
|
Тапсырма 2. Оқушылар кестені үлгі бойынша толтырады және жауаптарымен тексереді.
IV. Жұптық жұмыс.Оқушылар жазбаны қолданып, көпжақтың моделін құрастырады және оның түрін анықтайды.
1-ші оқушыға кесте
2-ші оқушыға кесте
|
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл
Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны
Сұрақтар топтамасы.
Оқулық 11-сынып.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Сабақтың соңы |
Үй тапсырмасы. 1.Дұрыс төртбұрышты пирамиданың биіктігі 7 см тең, ал табан қабырғасы 8 см. Бүйір қырын табыңыздар. 2. Тік призманың табандары катеттері 6см және 8см болатын тікбұрышты үшбұрыш. Гипотенузасыорналасқанжағыныңдиагоналі 26 см. Призманыңбиіктігінтабыңыздар. |
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Қысқа мерзімді жоспар №6-сабак
|
Ұзақ мерзімді жоспар бөлімі: Көпжақтар |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Дұрыс көпжақтар |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.1.6 - дұрыс көпжақтың анықтамасын білу, дұрыс көпжақтардың түрлерін ажырата білу; |
|
Сабақтың мақсаты: |
- дұрыс көпжақтың анықтамасын білу, дұрыс көпжақтардың түрлерін ажырата біледі; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
||||||||||||||||||||||||||||||
|
Сабақтың басы |
Октаэдрдің 6 жағы шаршы, ал сегіз жағы дұрыс алтыбұрыштар болатын фигура шығатындай етіп төбелерін кесіп алған. Пайда болған фигураның бетінің ауданын есептеңіз, егер берілген октаэдрдің қыры 24 бірлікке тең болса. |
Өткен материалды қайталау. 1) Қандай көпжақтар дұрыс деп аталады? 2) Дұрыс көпжақтардың бес түрін атап шығыңдар да, олар жөнінде әңгімелеп беріңдер. 3) Дұрыс: а) тетраэдрдің; б) гексаэдрдің; в) октаэдрдің; г) икосаэдрдің бетінің ауданын табыңыздар. Жауаптары: а) |
«Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
Түрлі түсті қима қағаздар
|
||||||||||||||||||||||||||||||
|
Сабақтың ортасы |
. Есептер шығару.Жұптық жұмыс.Оқушылар есептерді жұппен ақылдасып орындайды. 1) Кубтың қыры a-ға тең. Оның екі жағының диагональдары арқылы өтетін қиманың ауданын табыңдар. Жауабы: Іргелес жақтардың
диагональдары арқылы өтетін қиманың ауданы
2) DABC дұрыс тетраэдрінің қыры а-ға тең. ТетраэдрдіңАВС жағының центрі арқылы өтетін: a) BDC жағына параллель жазықтықпен; б) AD қырына перпендикуляр жазықтықпен қимасының ауданын табыңдар. Жауабы:
а) . Тест. 1) Қандай дұрыс көпжақтың жиырма төбесі бар? a) Тетраэдр b) Октаэдр c) Додекаэдр d) Икосаэдр 2) Қандай дұрыс көпжақта бір төбесіндегі барлық жазық бұрыштардың қосындысы 240о–қа тең? a) Куб b) Октаэдр c) Додекаэдр d) Икосаэдр 3) Дұрыс көпжақтарға қатысты қандай тұжырым дұрыс емес? a) Тек үш дұрыс көпжақтың ғана жақтары дұрыс үшбұрыш болады. b) Тек бір дұрыс көпжақтың ғана жағы квадрат болады. c) Тек бір дұрыс көпжақтың ғана жағы дұрыс алтыбұрыш болады. d) Тек бір дұрыс көпжақтың ғана жағы дұрыс бесбұрыш болады. 4) Қандай дұрыс көпжақтың он екі жағы бар? a) Куб b) Октаэдр c) Додекаэдр d) Икосаэдр 5) Дұрыс икосаэдрдің барлық жақтары дұрыс ... a) Үшбұрыштар b) Квадраттар c) Бесбұрыштар d) Алты бұрыштар 6) Дөңес көпжақ дұрыс деп аталады, егер оның жақтары: a) Дұрыс көпбұрыштар b) Тең көпбұрыштар c) Көпбұрыштар d) Тең дұрыс көпбұрыштардың қабырғаларының саны көпжақтың әр төбесіндегі қырлардың санына тең |
Топтық жұмыс.Оқушылар үш топқа бірігеді, әр топқа 3 тапсырмадан беріледі, содан соң әр топтан бір есептің шешу жолы тыңдалады. 1-топқа берілетін тапсырмалар 1) Тетраэдрдің, октаэдрдің, икосаэдрдің төбесіндегі жазық бұрыштардың қосындысын анықтаңыз.
2) Икосаэдрдің толық бетінің ауданы 480 см2. Бір жағының ауданын табыңыз.
3) Дұрыс үшбұрышты пирамида мен дұрыс тетраэдр ұғымдары арасында қандай байланыс бар? (дұрыс тетраэдр – дұрыс үшбұрышты пирамиданың дербес түрі) 2-топқа берілетін тапсырмалар 1) Додекаэдрдің барлық төбелеріндегі жазық бұрыштардың қосындысын табыңыз. Ескерту: дұрыс бесбұрыштың
бұрышын
2) Октаэдрдің қырының ұзындығы 6 см. Оның толық бетінің ауданын табыңыз.
3) Барлық қырлары тең болатын, бірақ өзі дұрыс болмайтын көпжаққа мысал келтір. (табаны ромб болатын, қырлары тең болатын пирамида). 3-топқа берілетін тапсырмалар 1) Қандай дұрыс көпжақтар дұрыс жазық бұрыштарға ие? (тетраэдр, октаэдр, икосаэдр) 2) Додекаэдрдің беті 180 см2. Оның жағының ауданын табыңыз.
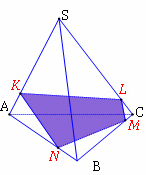
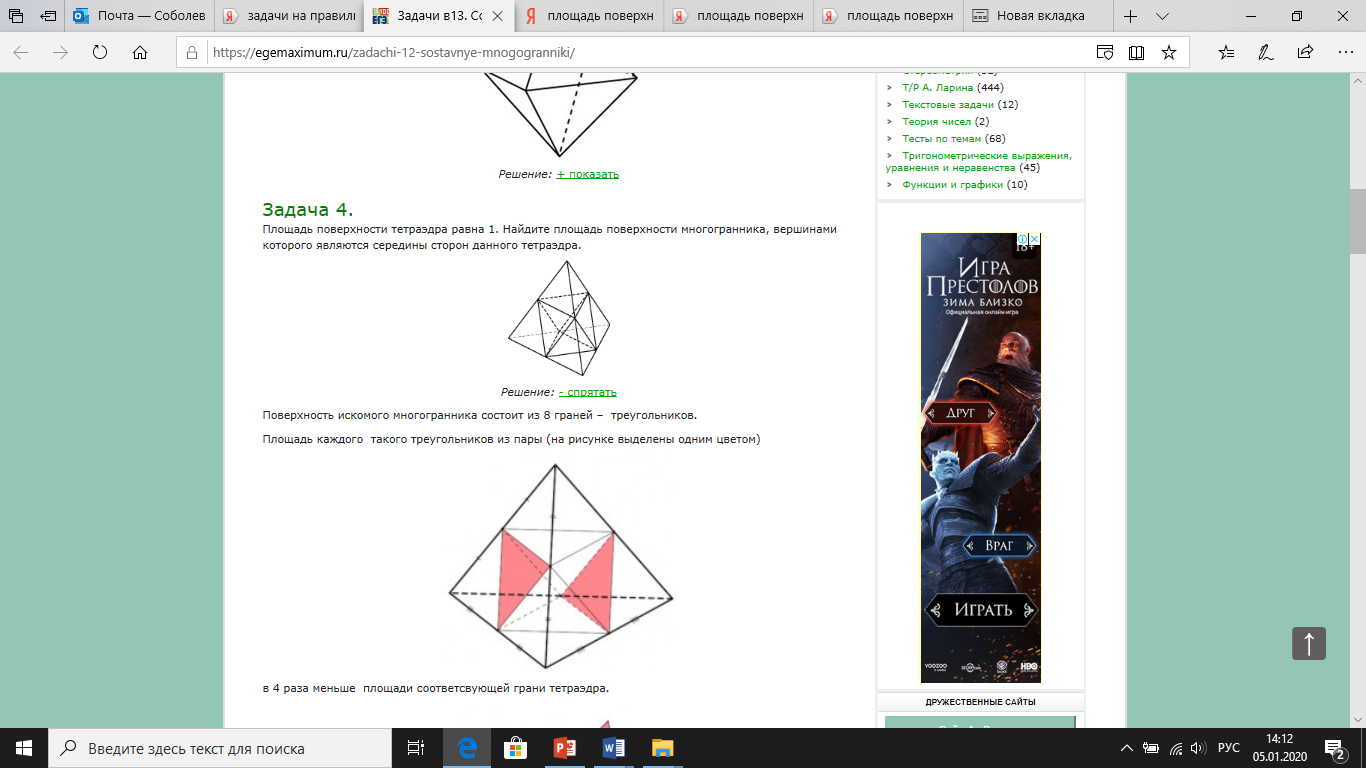
3) Қандай дұрыс пирамида (призма) дұрыс көпжақ болып табылады? (дұрыс тетраэдр, куб) Тетраэдрдың толық бетінің ауданы 1-ге тең. Қабырғаларын тең бөлікке бөліп, нүктелердің қиылысуынан тұратын көпжақтың толық бетінің ауданын тап.
Дайын жоспары бойынша 1-2, 3- тапсырмаларды шешу. №1. Қырлары 10 см болатын дұрыс тетраэдрдің биіктігін табыңыз. №2. Кристалл октаэдр пішіндес ортақ табандары бар екі дұрыс пирамидадан тұрады. Пирамиданың табан қырлары 6 см. Октаэдрдің биіктігі 14 см. Кристалдың бүйір бетінің ауданын табыңыз. №3. Текшенің қарама-қарсы жақтарындағы екі параллель емес диагоналдарының ұштары тетраэдрдің төбелері болып табылатынын дәлелдеңіз. Бағалау: оқушылар жеке жұмыс қорытындысы бойынша өз жұмысын бағалайды |
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны Сұрақтар топтамасы. Оқулық 11-сынып.
|
||||||||||||||||||||||||||||||
|
Сабақтың соңы |
. Үй тапсырмасы. №1. Дұрыс тетраэдрдің толық бетінің ауданын табыңыз, егер оның қыры b-ға тең болса? №2. Кубтың диагоналіa-ға тең. Кубтың толық бетінің ауданын есептеңіз. |
Кестені толтыру.
Кестенің көмегімен әр оқушы Эйлер формуласын қорытып шығаруға талпынады. Бірін-бірі тақтамен тексереді, бағалайды.
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
Қысқа мерзімді жоспар №7-сабак
|
Ұзақ мерзімді жоспар бөлімі: Кеңістіктегі түзу мен жазықтық теңдеулерінің қолданылуы |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Кеңістіктегі түзу мен жазықтықтың өзара орналасуы |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.2.6 – кеңістіктегі түзу мен жазықтықтың өзара орналасуын білу; |
|
Сабақтың мақсаты: |
– кеңістіктегі түзу мен жазықтықтың өзара орналасуын біледі; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|
Сабақтың басы |
|
Берілгені:
|
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
Түрлі түсті қима қағаздар
|
|
Сабақтың ортасы |
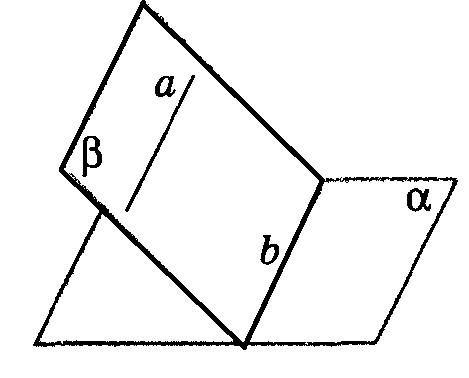
1)Түзу мен жазықтықтың өзара орналасуын қарастыру. Егер түзу мен жазықтықтың ортақ нүктелері жоқ болса онда оларды өзара параллель дейміз.
Теорема 1. Егер берілген жазықтықта жатпайтын түзу сол жазықтықта жататын белгілі бір түзуге параллель болса, онда ол жазықтықтың өзіне де параллель болады. Теорема
2. Берілгені:
Теорема 3.Егер өзара параллель екі түзудің біреуі берілген жазықтыққа параллель болса, онда екіншісі де берілген жазықтыққа параллель болады немесе сол жазықтықта жатады. 5. Жаңа тақырыпты бекіту. 1)Ұжымдық жұмыс. 1. Берілгені: 2. Берілгені: Дәлелдеукерек: 3. Берілгені: α
жазықтығы
АВС үшбұрышының АВ және АС қабырғаларын сәйкесінше
Бағалау стратегиясы. ұжымдық жұмысбарысында бірін-бірі бағалау, мұғалім бағалау жүзеге асырылады. Мұғалім оқушылардың жиі жіберетін қателері бойынша түсінік береді. Дифференциация күрделендіру принципі бойынша құрылған: деңгейден деңгейге біртіндеп ауысу. |
Жеке жұмыс. Оқушылар деңгейлік тапсырмаларды шығарады. Бірін-бірі бағалайды. 1-деңгей 1.
Берілгені:
2. Берілгені:
2-деңгей 3.
a)
b) Егер
4.
Бағалау стратегиясы. Жеке жұмыс барысында бірін-бірі бағалау, мұғалім бағалау жүзеге асырылады. Мұғалім оқушылардың жиі жіберетін қателері бойынша түсінік береді. Дифференциация күрделендіру принципі бойынша құрылған: деңгейден деңгейге біртіндеп ауысу. 1.
Берілгені:
2. Берілгені: ??∥?, ??∩?=?;??∩?=?. Дәлелдеукерек: ∆???~∆???.
Берілгені: α
жазықтығы АВС үшбұрышының АВ
және АС қабырғаларын сәйкесінше
|
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны Сұрақтар топтамасы. Оқулық 11-сынып.
|
|
Сабақтың соңы |
.Сабақты қорытындылау. Рефлексия «Бес саусақ» әдісі бойынша әрбір оқушы рефлексия жасайды |
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
Қысқа мерзімді жоспар №8-сабак
|
Ұзақ мерзімді жоспар бөлімі: Кеңістіктегі түзу мен жазықтық теңдеулерінің қолданылуы |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Кеңістіктегі түзу мен жазықтықтың өзара орналасуы |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.2.6 – кеңістіктегі түзу мен жазықтықтың өзара орналасуын білу; |
|
Сабақтың мақсаты: |
– кеңістіктегі түзу мен жазықтықтың өзара орналасуын біледі; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|
Сабақтың басы |
Қосымша 1 1.
2. |
Кеңістіктегі түзу және жазықтықтың теңдеуінің негізгі түрлерін қайталау. Мұғалім оқушыларға кеңістіктегі түзу және жазықтықтағы теңдеулердің негізгі түрлерін еске түсіруді ұсынады. 1. Түзудің канондық теңдеуі. 2. Екі берілген нүкте арқылы өтетін түзу теңдеуі. 3. Түзудің параметрлік теңдеуі. 4. Жазықтықтың жалпы теңдеуі.
|
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
Түрлі түсті қима қағаздар
|
|
Сабақтың ортасы |
.
Берілгені:
|
. a)
b)
Егер
|
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны Сұрақтар топтамасы. Оқулық 11-сынып.
|
|
Сабақтың соңы |
2. Түзу А(3; -1; 0)
жәнеВ(х; -7; 3) нүктелері арқылы
өтеді және |
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
Қысқа мерзімді жоспар №9-сабак
|
Ұзақ мерзімді жоспар бөлімі: Кеңістіктегі түзу мен жазықтық теңдеулерінің қолданылуы |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтық |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.4.1 – нүктеден жазықтыққа дейінгі арақашықтықты табу формуласын білу және оны есептер шығаруда қолдану; |
|
Сабақтың мақсаты: |
– нүктеден жазықтыққа дейінгі арақашықтықты табу формуласын біледі және оны есептер шығаруда қолданады; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|
Сабақтың басы |
Ұйымдастыру кезеңі. 1. Оқушылармен сәлемдесу 2. Үй тапсырмасын тексеру. 3. Тақырыпты, сабақ мақсатын, бағалау критерийлерін анықтау. |
Білімді жаңғырту
жазыңыз.
|
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» |
Түрлі түсті қима қағаздар
|
|
Сабақтың ортасы |
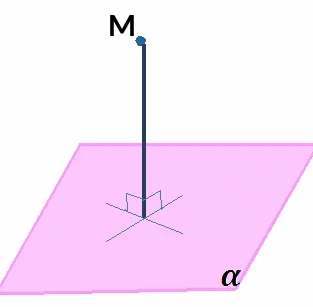
Жаңа материалды меңгерту. Нүктеден жазықтыққа дейінгі арақашықтық деп сол нүктеден жазықтыққа түсірілген перпендикулярдың ұзындығын айтамыз.
Бұл қашықтықты анықтау үшін: - М нүктесі арқылы жазықтыққа жүргізілген перпендикуляр түзудің теңдеуін жазыңыз; - түзу мен жазықтықтың қиылысу нүктесінің координаттарын анықтаңыз; - М нүктесі түзу мен жазықтықтың қиылысу нүктесіне дейінгі қашықтықты табыңыз. Ал, бұл қашықтықты анықтау формуласы:
Мысал – 1.
Жазықтықтың нормаль
векторы:
Жауабы:
Дескриптор:
- нүктеден жазықтыққа дейінгі арақашықтықты формула арқылы дұрыс табады. |
Үжымдық жұмыс 1) А (7; 5; 3) нүктесі мен α: 3х + 2у + z = 6 жазықтығы берілген. а) А нүктесі арқылы өтіп, α жазықтығына перпендикуляр болатын l түзуінің теңдеуін табыңыз; b) l түзуі мен α жазықтығының қиылысу нүктесі Р-ны анықтаңыз; c) А және Р нүктелерінің арақашықтығын табыңыз. 2)λ жазықтығыныңжалпытеңдеуі Ax + By + Cz + D= 0 болсын. M0(x0; y0;z0) - λ жазықтығынатиістіемеснүкте. M0нүктесінен λ жазықтығынадейінгіарақашықтықтытабыңыз. 3) M0(2; 3; 4) нүктесінен 4х+3у+12z-5=0 жазықтығына дейінгі арақашықтықты табыңыз.
Дескриптор:
қолданады; -Нүктеден жазықтыққа дейінгі арақашықтықты табады Сыныптық (ұжымдық) жұмыс ұйымдастыру, бірі – біріне түсіндіре отырып орындауғы ұсыну. № 1. Координаттар бас
нүктесінен № 2.
Жұппен жұмыс тапсырмалары. № 3.
Жауабы: № 4.
Жауабы:
Дескриптор:
- нүктеден жазықтыққа дейінгі арақашықтықты формула арқылы дұрыс табады. |
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны Сұрақтар топтамасы. Оқулық 11-сынып.
|
|
Сабақтың соңы |
Сабық соңында оқушылар рефлексия жасайды: - не білдім, не үйрендім? - не түсініксіз болды? - нені толықтыруым қажет? |
Шығармашылық тапсырма (зерттеу жұмысы)
Жауабы:
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
Қысқа мерзімді жоспар №10-сабак
|
Ұзақ мерзімді жоспар бөлімі: Кеңістіктегі түзу мен жазықтық теңдеулерінің қолданылуы |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтық |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.4.1 – нүктеден жазықтыққа дейінгі арақашықтықты табу формуласын білу және оны есептер шығаруда қолдану; |
|
Сабақтың мақсаты: |
– нүктеден жазықтыққа дейінгі арақашықтықты табу формуласын біледі және оны есептер шығаруда қолданады; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|
Сабақтың басы |
. Жұппен зерттеу жүргізу Егер А(1; 1; 1) жәнеВ(2; -1; 0) болса, α: х – 4у + 2z + 5 = 0 жазықтығы АВ түзуін қияды ма? (жазықтық АВ кесіндісін қияды ма? |
Жеке жұмыс 1.ρ: 2х + 4у - 4z – 6 = 0 жазықтығы мен М (0; 3; 6) нүктесінің арақашықтығын табыңыз. 2. А (1; 2; 3) нүктесінен α: 2х + 3у – z + 1 = 0 жазықтығына дейінгі қашықтықты табыңыз. 3. М(-2;-4;3) нүктесіненρ: 2х – у + 2z + 3 = 0 жазықтығына дейінгі қашықтықты табыңыз. Дескриптор: -Нүктеден жазықтыққа дейінгі арақашықтықты табады
|
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: |
|
|
Сабақтың ортасы |
) а) М(1; 1; 1) нүктесінен ρ: х + у – 2z – 6 = 0 жазықтығына дейінгі арақашықтықты табыңыз. б) Мнүктесіне ρ: х + у – 2z – 6 = 0 жазықтығына қатысты симметриялы болатын N нүктесін анықтаңыз. Шешуі: а) б) М
нүктесінен ρ жазықтығына жүргізілген
перпендикуляр түзудің параметрлік теңдеуін құрамыз:
Жауабы: |
Үжымдық жұмыс 1) А (7; 5; 3) нүктесі мен α: 3х + 2у + z = 6 жазықтығы берілген. а) А нүктесі арқылы өтіп, α жазықтығына перпендикуляр болатын l түзуінің теңдеуін табыңыз; b) l түзуі мен α жазықтығының қиылысу нүктесі Р-ны анықтаңыз; c) А және Р нүктелерінің арақашықтығын табыңыз. 2)λ жазықтығыныңжалпытеңдеуі Ax + By + Cz + D= 0 болсын. M0(x0; y0;z0) - λ жазықтығынатиістіемеснүкте. M0нүктесінен λ жазықтығынадейінгіарақашықтықтытабыңыз. 3) M0(2; 3; 4) нүктесінен 4х+3у+12z-5=0 жазықтығына дейінгі арақашықтықты табыңыз. Дескриптор:
қолданады; -Нүктеден жазықтыққа дейінгі арақашықтықты табады |
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны Сұрақтар топтамасы. Оқулық 11-сынып.
|
|
Сабақтың соңы |
Сабақты қорытындылау -нүктенің жазықтықтыққа дейінгі арақышықтықты табу формуласын біледі; -есептер шешуде нүктенің жазықтықтыққа дейінгі арақышықтықты табу формуласын қолданады. Тапсырмалар төменнен жоғары деңгейге ауысады. Мұғалім оқушылардың қиналған түсында қолдаубілдіреді. Әр бөлім бойынша кері байланыс береді. |
Үй тапсырмасы 1.М(3; 5; 8) нүктесіне Oх жазықтығына қатысты симметриялы нүктеден 3х-у-4 z=0 жазықтығына дейінгі арақашықтықты табыңыз. 2. а) М(1; 1; 1) нүктесінен ρ: х + у – 2z – 6 = 0 жазықтығына дейінгі арақашықтықты табыңыз. б) М нүктесіне ρ: х + у – 2z – 6 = 0 жазықтығына қатысты симметриялы болатын N нүктесін анықтаңыз |
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
Қысқа мерзімді жоспар №11-сабак
|
Ұзақ мерзімді жоспар бөлімі: Кеңістіктегі түзу мен жазықтық теңдеулерінің қолданылуы |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтық |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.4.1 – нүктеден жазықтыққа дейінгі арақашықтықты табу формуласын білу және оны есептер шығаруда қолдану; |
|
Сабақтың мақсаты: |
– нүктеден жазықтыққа дейінгі арақашықтықты табу формуласын біледі және оны есептер шығаруда қолданады; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
||||||||||||||||||||||||
|
Сабақтың басы |
Топпен жұмыс
Шешуі:М нүктесіне Oxz жазықтығына қатысты симметриялы
нүкте (3; -5; 8)
болады. Олай болса,
ізделінді
арақашықтық Жауабы: |
. Өткенді қайталау. Мұғалім тақтада әртүрлі тапсырмаларды көрсетеді, ал оқушылар оның жауабын шағын тақтаға жазып, көрсетеді. Дескрипторлар: - формуланы қолданып нүктеден жазықтыққа дейінгі арақашықтықты табады.
|
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
Түрлі түсті қима қағаздар
|
||||||||||||||||||||||||
|
Сабақтың ортасы |
Жауабы:
Дескрипторлар: - жазықтықтың теңдеуін құрады; - формуланы қолданып нүктеден жазықтыққа дейінгі арақашықтықты табады; - өзге нүктеге жазықтыққа қатысты симметриялы нүктенің координаталарын анықтайды. |
Дағдыларды жетілдіру. Жеке жұмыс Жаттығуға арналған тапсырмалар:
Дескрипторлар: - жазықтықтың теңдеуін құрады; - формуланы қолданып нүктеден жазықтыққа дейінгі арақашықтықты табады. |
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл
Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны
Сұрақтар топтамасы.
Оқулық 11-сынып.
|
||||||||||||||||||||||||
|
Сабақтың соңы |
. Сабақты қорытындылау.
|
Екі нүкте арасындағы қашықтық осы нүктелерді қосатын кесінді ұзындығына тең. Мысал 1. A(-1, 3, 3) және B(6, 2, -2) нүктелерінің ара қашықтығын табыңдар. Жауабы:
5
2. Нүкте мен түзудің ара қашықтығы берілген нүктеден түзуге түсірілген перпендикуляр ұзындығына тең. Мысал 2.ABCDA1B1C1D1кубтың қыры 1 см-ге тең. А нүктесінен ВD1 түзуіне дейінгі қашықтықты табыңыз. Жауабы:
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
||||||||||||||||||||||||
Қысқа мерзімді жоспар №12-сабак
|
Ұзақ мерзімді жоспар бөлімі: Кеңістіктегі түзу мен жазықтық теңдеулерінің қолданылуы |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Кеңістіктегі түзулер арасындағы бұрышты, түзу мен жазықтық арасындағы бұрышты табу |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.4.2 – түзулер арасындағы бұрышты (түзулердің теңдеулері бойынша) табу; 11.4.3 – координаталардағы түзулердің параллельдігі мен перпендикулярлығы шартын есептер шығаруда қолдану; 11.4.5 – түзу мен жазықтық арасындағы бұрышты табу; |
|
Сабақтың мақсаты: |
– түзулер арасындағы бұрышты (түзулердің теңдеулері бойынша) табады; – координаталардағы түзулердің параллельдігі мен перпендикулярлығы шартын есептер шығаруда қолданады; – түзу мен жазықтық арасындағы бұрышты табады; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|
Сабақтың басы |
Ұйымдастыру кезеңі. - оқушылардың зейінін шоғырландыру - ОМ таныстыру, оқушылармен бірлесіп сабақтың мақсатын, жетістік критерийін анықтау - «ЖАДА» анықтау |
Білімдерін жаңғырту.Фронтальды жұмыс. Мұғалім оқушыларға кеңістіктегі түзудің теңдеулерінің түрлерін қайталауды ұсынады: түзудің канондық теңдеуі, параметрлік теңдеуі, түзудің теңдеуінің бір түрінен екінші түріне қалай өтуге болатындығын анықтау. Содан кейін мұғалім оқушыларға жазықтықта түзулердің қалай орналасатынын еске түсіру ұсынады |
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: |
Түрлі түсті қима қағаздар
|
|
Сабақтың ортасы |
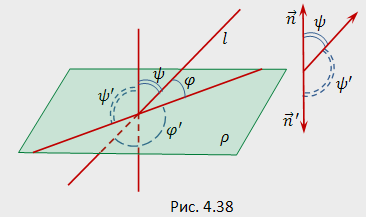
Жаңа материалды меңгеру. Кеңістіктегі екі түзу арасындағы бұрыш анықтамасы. Мұғалім кеңістіктегі түзулердің өзара орналасу жағдайларын қарастыруды ұсынады.Қосымша 1 тапсырмаларын қарастыру. Кеңістіктегі түзулердің өзара орналасуы Кеңістіктегі екі түзудің орналасуы: 1) айқас; 2) бір нүктеде қиылысады; 3) параллель; 4) сәйкес. Бірінші жағдай басқаларға қарағанда ерекше. Екі түзу айқас деп аталады егер олар қиылыспайтын болса және бір жазықтықта жатпайтын болса. (Қолдарыңызды бірін жоғары бірін алға қарай созыңыздар, міне айқас түзуге тікелей мысал) № 2-4 пунктерде түзілер міндетті түрде бір жазықтықта жатады. Кеңістіктегі түзулердің өзара орналасуын қалай анықтауға болады? Кеңістіктегі екі түзуді қарастырайық: – – Түсініктірек болу үшін сызбасын салайық:
Жоғарыдағы сызбада айқас түзулер бейнеленген. Осы түзулер арасындағы бұрышты қалай анықтаймыз? Кеңістіктегі түзулер арасындағы бұрыш ұғымы қиылысатын түзулер үшін ғана емес, кеңістікте қиылыспайтын және бір жазықтықта жатпайтын айқас түзулер үшін де анықталған. Айқас түзулер арасындағы бұрыш осы түзулерге параллель қиылысатын түзулер арасындағы бұрышты айтады. Яғни бағыттаушы векторлар арасындағы бұрышпен анықтауға болады. Ол формула төмендегідей.:
мұндағы Дербес жағдай,
егер |
О Суреттегі А бұрышы
– жазықтықтың Енді Шешуі: (2;3;1)–
жазықтықтың нормаль векторы,
(-1;2;5)–
түзудің бағыттаушы векторы.
Осы екі вектор
арасындағы бұрышты табу үшін Демек берілген түзу мен жазықтық арасындағы бұрыш шамамен 26 °. Т
4. Білім және білік дағдыларын бекіту. Топтық жұмыс 1)
2)
3) Координат басы мен М(2; -1; 3) нүктесі арқылы өтетін түзу мен ρ: 3х – у + 2z – 4 = 0 жазықтығы арасындағы бұрышты табыңыз. М нүктесінен ρ жазықтығына дейінгі қашықтықты табыңыз. 4)
ρ:
Дескриптор:
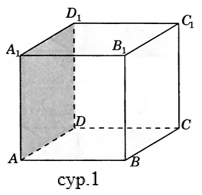
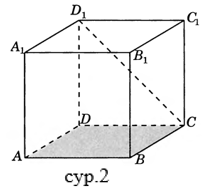
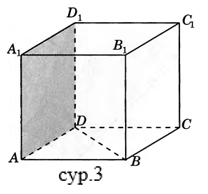
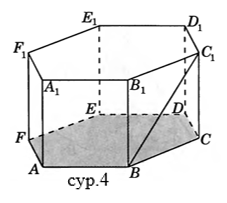
Жұптық жұмыс А деңгейі 1) A…D1 кубында AB түзуі мен ADD1жазықтық арасындағы бұрышты табыңыз (сур.1) 2) A…D1 кубында СD1түзуі мен AВС жазықтық арасындағы бұрышты табыңыз(сур.2) 3) A…D1 кубында DВтүзуі мен ADD1жазықтық арасындағы бұрышты табыңыз(сур.3) 4) A…F1 дұрыс алтыбұрышты призмада барлық қабырғалары 1 тең, ВС1түзуі мен AВС жазықтық арасындағы бұрышты табыңыз (сур.4)
В деңгейі 1) A…D1 кубында СА1 түзуі мен AВ1D1жазықтық арасындағы бұрышты табыңыз(сур.1) 22) A…F1 дұрыс алтыбұрышты призмада барлық қабырғалары 1 тең, ВD1 түзуі мен AВС жазықтық арасындағы бұрышты табыңыз(сур.2) 3) SABCD дұрыс төртбұрышты призмада барлық қабырғалары 1 тең, SA түзуі мен SВD жазықтық арасындағы бұрышты табыңыз(сур.3)
С деңгейі 1) A…D1 кубында BС түзуі мен AВ1D1 жазықтық арасындағы бұрыштың синусын табыңыз.
Дескриптор:
түзу мен жазықтықтың арасындағы бұрышты табады. |
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны Сұрақтар топтамасы. Оқулық 11-сынып.
|
|
Сабақтың соңы |
Мұғалім олардың жетістіктерін талқылай отырып, оқу мақсаттарына қайта оралады. Ары қарай жоспарлау үшін оқушыларға келесі сұрақтар қойылады: - не білдім, нені үйрендім; - не түсініксіз болып қалды; - қандай сұрақпен жұмыс жасау керек. Сұрақтарды ауызша немесе жазбаша түрде талқылауға болады. |
Үй тапсырмасы Бағалау критерийлерінің қорытындысы бойынша үй жұмысы беріледі. Үй жұмысына түсініктеме беру. 1)
2)
3)
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
Қысқа мерзімді жоспар №13-сабак
|
Ұзақ мерзімді жоспар бөлімі: Кеңістіктегі түзу мен жазықтық теңдеулерінің қолданылуы |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Кеңістіктегі түзулер арасындағы бұрышты, түзу мен жазықтық арасындағы бұрышты табу |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.4.2 – түзулер арасындағы бұрышты (түзулердің теңдеулері бойынша) табу; 11.4.3 – координаталардағы түзулердің параллельдігі мен перпендикулярлығы шартын есептер шығаруда қолдану; 11.4.5 – түзу мен жазықтық арасындағы бұрышты табу; |
|
Сабақтың мақсаты: |
– түзулер арасындағы бұрышты (түзулердің теңдеулері бойынша) табады; – координаталардағы түзулердің параллельдігі мен перпендикулярлығы шартын есептер шығаруда қолданады; – түзу мен жазықтық арасындағы бұрышты табады; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
||||||||||||||
|
Сабақтың басы |
Өткен тақырыпты қайталау. Оқушылар колинеар және
перпендикуляр векторлардың анықтамасын еске түсірсін. Содан соң
колинеарлық |
Ұйымдастыру кезеңі:
3. Білімдерін белсендендіру. Білімдерін белсендендіру мақсатында өткен материалдарды қайталау. Сыныпты 1,2,3.. сандарын санау арқылы екі топқа бөліңіз. Тақ сандар бірінші топ, жұп сандар екінші топ. Әр топқа А3 қағазын таратыңыз. Әр топ мүшелері өтілген «жазықтықтар арасындағы бұрыш» тақырыбы бойынша негізгі ақпараттарды постерге жазады. Әр топ жазған ақпаратты тақтада айтады. Мұғалім қажет болған жағдайда толықтырулар енгізеді және түсіндіреді. Әр топқа жұмыс алгоритмін таратып беріледі
|
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
Түрлі түсті қима қағаздар
|
||||||||||||||
|
Сабақтың ортасы |
4.Ұжымдық жұмыс.
Өзара тексеруді ұйымдастырыңыз. |
Топтық жұмыс Оқушыларды екі топқа бөліңіз. Әр топқа келесі тапсырманы ұсыныңыз:
Нәтижесінде топтар өз мысалдарын көрсетіп, кеңістіктегі түзулердің параллельдік және перпендикулярлық шарттарын анықтайды:
|
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл
Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны
Сұрақтар топтамасы.
Оқулық 11-сынып.
|
||||||||||||||
|
Сабақтың соңы |
Мұғалім олардың жетістіктерін талқылай отырып, оқу мақсаттарына қайта оралады. Ары қарай жоспарлау үшін оқушыларға келесі сұрақтар қойылады: - не білдім, нені үйрендім; - не түсініксіз болып қалды; - қандай сұрақпен жұмыс жасау керек. Сұрақтарды ауызша немесе жазбаша түрде талқылауға болады. |
Үй жұмысы.Оқушыларды жұптастырып, практикалық тапсырма беріңіз.
Жауабы: (0;4;3); |
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|
Қысқа мерзімді жоспар №14-сабак
|
Ұзақ мерзімді жоспар бөлімі: Кеңістіктегі түзу мен жазықтық теңдеулерінің қолданылуы |
Мектеп: |
|
Педагогтің Аты,Тегі, Әкесінің аты |
|
|
Күні: |
|
|
Сыныбы: 11 |
Қатысушылар саны: Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Кеңістіктегі түзулер арасындағы бұрышты, түзу мен жазықтық арасындағы бұрышты табу |
|
Оқу бағдарламасына сәйкес оқыту мақсаты |
11.4.2 – түзулер арасындағы бұрышты (түзулердің теңдеулері бойынша) табу; 11.4.3 – координаталардағы түзулердің параллельдігі мен перпендикулярлығы шартын есептер шығаруда қолдану; 11.4.5 – түзу мен жазықтық арасындағы бұрышты табу; |
|
Сабақтың мақсаты: |
– түзулер арасындағы бұрышты (түзулердің теңдеулері бойынша) табады; – координаталардағы түзулердің параллельдігі мен перпендикулярлығы шартын есептер шығаруда қолданады; – түзу мен жазықтық арасындағы бұрышты табады; |
Сабақтың барысы:
|
Сабақ кезеңі/Уақыты |
Оқулықпен жұмыс. |
Оқушының іс-әрекеті |
Бағалау |
Ресурстар |
|
Сабақтың басы |
Ұйымдастыру кезеңі: - оқушылардың назарын шоғырландыру; - оқушылармен бірге оқу мақсатын анықтау - оқушылардың «жақын арадағы дамуын» анықтау. Үй тапсырмасын тексеру. |
1) 2)
3) Координат басы мен М(2; -1; 3) нүктесі арқылы өтетін түзу мен ρ: 3х – у + 2z – 4 = 0 жазықтығы арасындағы бұрышты табыңыз. М нүктесінен ρ жазықтығына дейінгі қашықтықты табыңыз. 4)
ρ:
Дескриптор:
жауабын табады. |
Мұғалім ұйымдастыру кезеңінде белсенділік танытқан оқушыларды «Мадақтау сөз» әдісіарқылы бағалайды: «Жарайсың! Жақсы! Өте жақсы! Талпын!» |
Түрлі түсті қима қағаздар
|
|
Сабақтың ортасы |
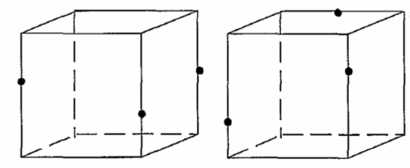
А деңгейі 1) A…D1кубындаAB түзуі мен ADD1жазықтық арасындағы бұрышты табыңыз (сур.1) 2) A…D1кубындаСD1түзуі мен AВС жазықтық арасындағы бұрышты табыңыз(сур.2) 3) A…D1кубындаDВтүзуі мен ADD1жазықтық арасындағы бұрышты табыңыз(сур.3) 4) A…F1дұрысалтыбұрыштыпризмадабарлыққабырғалары 1 тең, ВС1түзуі мен AВС жазықтық арасындағы бұрышты табыңыз (сур.4)
В деңгейі 1) A…D1 кубында СА1 түзуі мен AВ1D1жазықтық арасындағы бұрышты табыңыз(сур.1) 22) A…F1 дұрыс алтыбұрышты призмада барлық қабырғалары 1 тең, ВD1 түзуі мен AВС жазықтық арасындағы бұрышты табыңыз(сур.2) 3) SABCD дұрыс төртбұрышты призмада барлық қабырғалары 1 тең, SA түзуі мен SВD жазықтық арасындағы бұрышты табыңыз(сур.3)
|
Деңгейлік тапсырмалар. Оқушыларға сараланған тапсырмалар шығаруды ұсыныңыз. А деңгейі.
Жауабы:a= -5;
Жауабы: В деңгейі.
Шешуі:(3;-1;a)– берілген түзудің бағыттаушы
векторы, Жауабы:a=6,
Шешуі:
(2;
a;
-5)– берілген түзудің бағыттаушы
векторы, Жауабы: -2; Сдеңгейі.
Шешуі:
Егер
Жауабы:
Егер
Жауабы:
Шешуі:α: x – 7y + 5z – 4= 0
жәнеβ: 2x + 3y + tz + 1 =
0жазықтықтарының
нормаль векторлары сәйкесінше Жауабы: |
Дескриптор: -1-ші сұраққа жауап береді. 1-балл -2-ші сұраққа жауап береді. 1-балл -3-ші сұраққа жауап береді. 1-балл Әрбір дұрыс жауапка 1 балл қойылады
|
ДК экраны Сұрақтар топтамасы. Оқулық 11-сынып.
|
|
Сабақтың соңы |
Рефлексия Мұғалім сабақ мақсаттарына қайтып оралады, оқушылардың жетістіктерінің деңгейін айтады. Келесі сабақтарды жоспарлау мақсатында оқушыларға келесі сөйлемдерді толықтыру ұсынылады: Мен … білдім Мен … үйрендім Маған … ұнады Менде … деген сұрақ бар Маған … қиын болды Сұрақтар ауызша немесе жазбаша талқылана алады. |
1)
2)
3)
|
Бағалау. Оқушылар бір-бірін ауызша критерий бойынша бағалайды. |
|








 см2
см2


















 см,
табанының қабырғасы
см,
табанының қабырғасы  см-ге тең болатын PABC дұрыс үшб
см-ге тең болатын PABC дұрыс үшб

































 см2
см2 см2
см2 см2
см2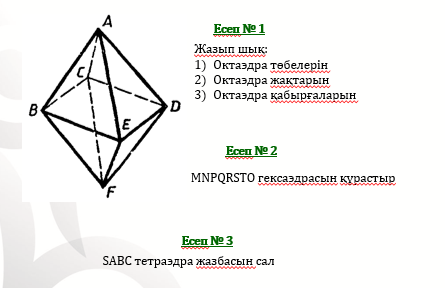
 ; б)
; б)  ;
в)
;
в)  ;
г)
;
г)  .
.












 -ді табыңыз.
-ді табыңыз.


 - трапеция,
- трапеция,
 - орта
сызығы;
- орта
сызығы;  . Дәлелдеу керек:
. Дәлелдеу керек:  және
және қабырғалары
қабырғалары


 және
және нүктелерінде
қияды.
нүктелерінде
қияды.

 -ны
табыңыз.
-ны
табыңыз.












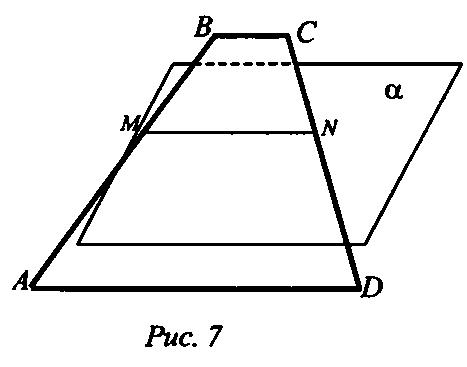
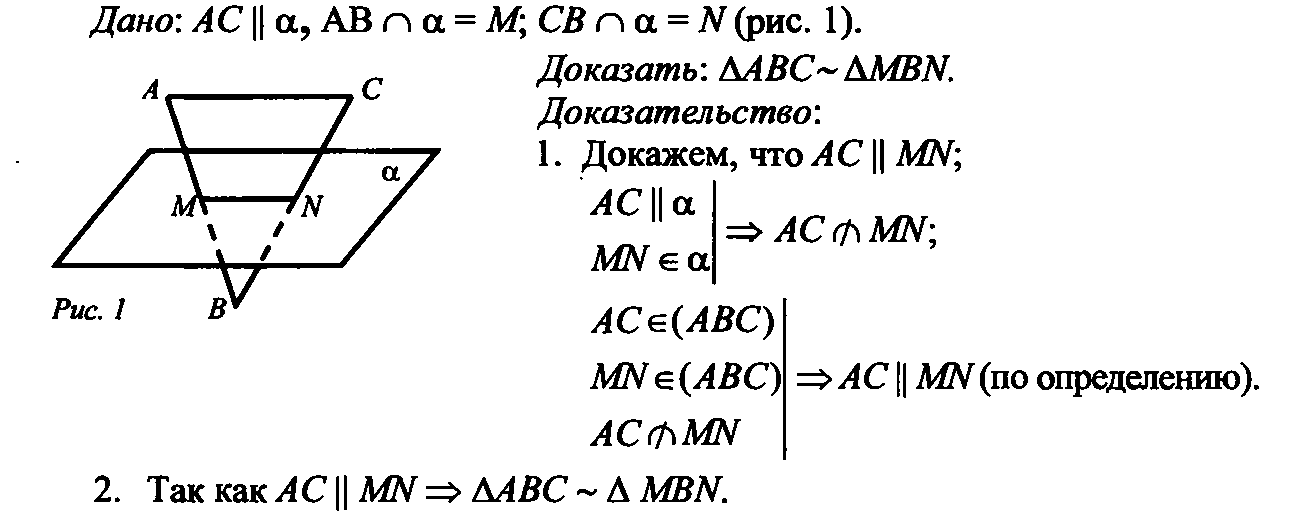

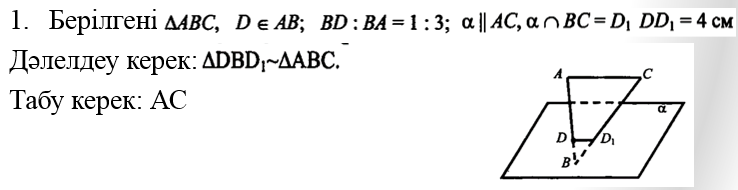
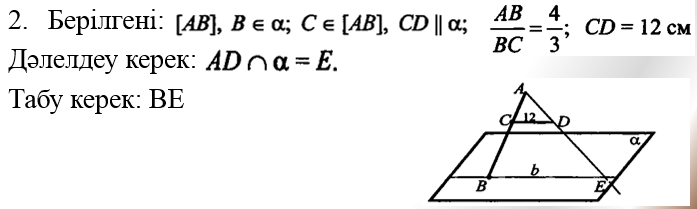




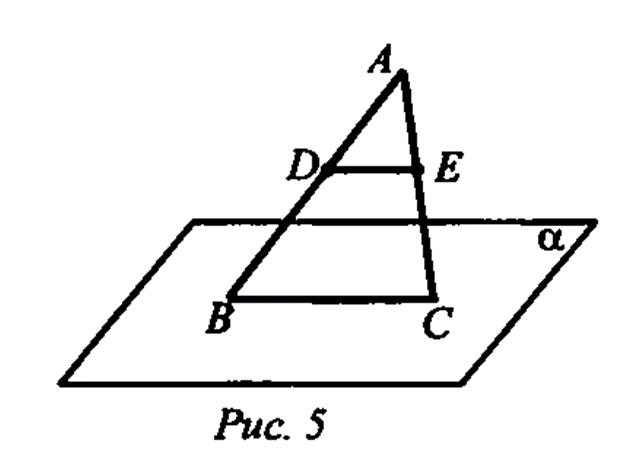
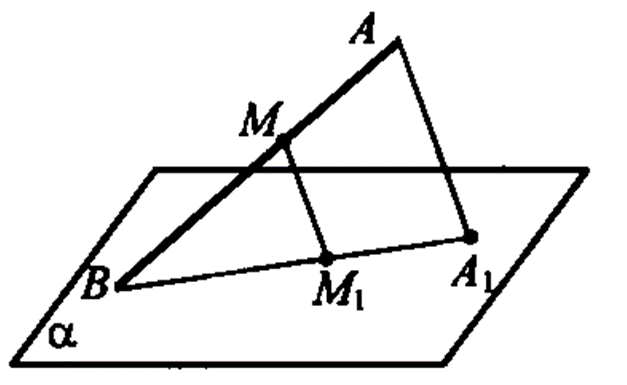
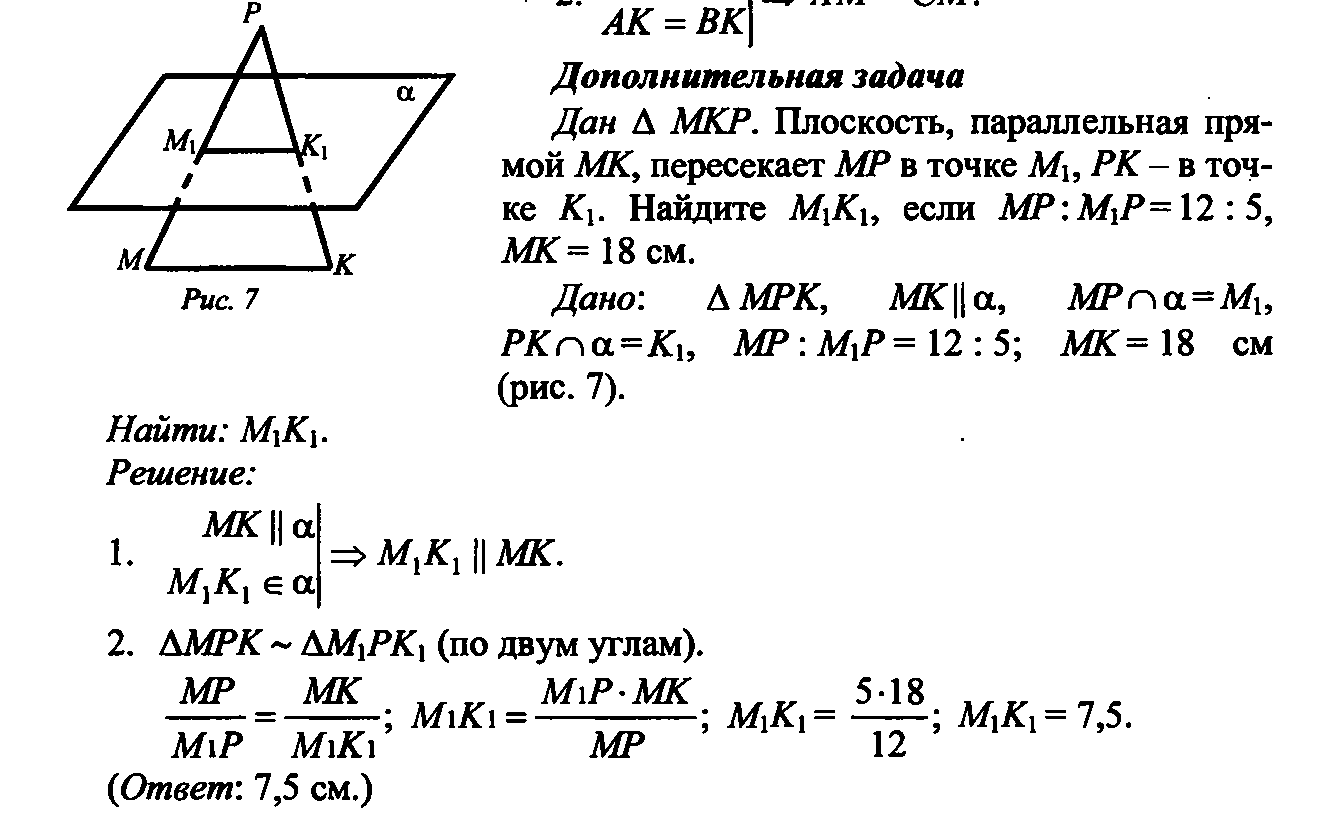








 .
. .
.
















 .
.






 ;
;











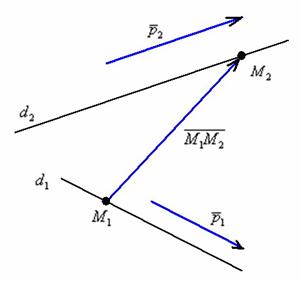





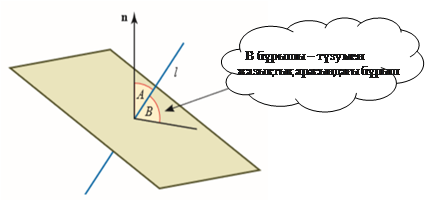 қушыларға
түзу мен жазықтық арасындағы бұрыштың анықтамасын еске түсіруді
және сызбасын орындауды тапсырыңыз. Оқушылармен
қушыларға
түзу мен жазықтық арасындағы бұрыштың анықтамасын еске түсіруді
және сызбасын орындауды тапсырыңыз. Оқушылармен




 алқылаудан
кейін оқушылар келесі тұжырымды қорытады:
алқылаудан
кейін оқушылар келесі тұжырымды қорытады:














 = {1; 2
= {1; 2 = {4; 8
= {4; 8 = {5; 10
= {5; 10 = {0; 6; 10}
= {0; 6; 10}  = {9;
= {9;  және
және

 вектор
вектор )
)  = (m
= (m = (2
= (2 = (4
= (4

 ,
, .
.


 - 4.
- 4. .
. 






 уретте
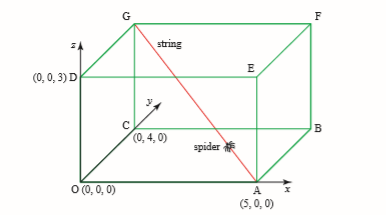
қабырғалары, едені және төбесі тіктөртбұрыш болатын бөлме
кескінделген. А және
уретте
қабырғалары, едені және төбесі тіктөртбұрыш болатын бөлме
кескінделген. А және

 ;
;


 ,
,  .
.


 .
. 



 .
. 
 .
.

 .
. ;
;


 .
.  .
.