Ашық сабақ, ҚМЖ, көрнекілік, презентация жариялап
2 млн. ₸ табыс табыңыз!
МИНИСТРЛІКПЕН КЕЛІСІЛГЕН КУРСҚА ҚАТЫСЫП, АТТЕСТАЦИЯҒА ЖАРАМДЫ СЕРТИФИКАТ АЛЫҢЫЗ!
Сертификат Аттестацияға 100% жарамды
ТОЛЫҚ АҚПАРАТ АЛУ 
Квадрат түбірлері бар өрнектерді түрлендіру. Есеп шығару
Материал туралы қысқаша түсінік
8.1.2.3 көбейткішті квадрат түбір белгісінің алдына шығару және көбейткішті квадрат түбір белгісінің астына алу;
8.1.2.4 бөлшек бөлімін иррационалдықтан арылту;
8.1.2.5 құрамында түбір таңбасы бар өрнектерді түрлендіруді орындау;
8.1.2.6 нақты сандарды салыстыру
Авторы:
Автор материалды ақылы түрде жариялады.
Сатылымнан түскен қаражат авторға автоматты түрде аударылады.
Толығырақ
16 Қазан 2018
649
0 рет жүктелгенТегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!
Дипломдар мен сертификаттарды алып үлгеріңіз!
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 18
Материалдың қысқаша түсінігі
1 слайд
Сабақтың
тақырыбы
Квадрат
түбірлері бар
өрнектерді
түрлендіру.
Есеп шығару.
1 слайд
Сабақтың тақырыбы Квадрат түбірлері бар өрнектерді түрлендіру. Есеп шығару.
2 слайд
Сабақтың
мақсаты
8.1.2.3 көбейткішті квадрат түбір
белгісінің алдына шығару және
көбейткішті квадрат түбір белгісінің
астына алу;
8.1.2.4 бөлшек бөлімін
иррационалдықтан арылту;
8.1.2.5 құрамында түбір таңбасы бар
өрнектерді түрлендіруді орындау;
8.1.2.6 нақты сандарды салыстыру;
2 слайд
Сабақтың мақсаты 8.1.2.3 көбейткішті квадрат түбір белгісінің алдына шығару және көбейткішті квадрат түбір белгісінің астына алу; 8.1.2.4 бөлшек бөлімін иррационалдықтан арылту; 8.1.2.5 құрамында түбір таңбасы бар өрнектерді түрлендіруді орындау; 8.1.2.6 нақты сандарды салыстыру;
3 слайд
Қызығушылықты ояту
« Өз жартыңды тап »
3 слайд
Қызығушылықты ояту « Өз жартыңды тап »
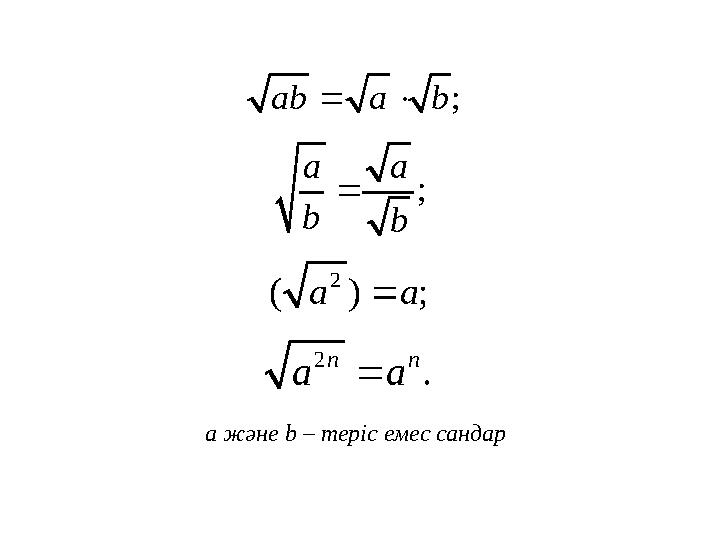
4 слайд
2
( ) ;a a
;ab a b
;
a a
bb
2
.
n n
a a
а және b – теріс емес сандар
4 слайд
2 ( ) ;a a ;ab a b ; a a bb 2 . n n a a а және b – теріс емес сандар
5 слайд
Оқушыға хат
•Бөлшектің бөлімін иррационалдықтан босату дегеніміз-
__________________________________________________________
•__________________________________________________________
•1) егер бөлшектің бөлімі __________________________ түрде болса,
•онда _____________________________________________________
•__________________________________________________________
•2) егер бөлшектің бөлімі __________________________ түрде болса,
•онда _____________________________________________________
•__________________________________________________________
•3)
____________________________________________________________
________________________ мұқият бол.
5 слайд
Оқушыға хат •Бөлшектің бөлімін иррационалдықтан босату дегеніміз- __________________________________________________________ •__________________________________________________________ •1) егер бөлшектің бөлімі __________________________ түрде болса, •онда _____________________________________________________ •__________________________________________________________ •2) егер бөлшектің бөлімі __________________________ түрде болса, •онда _____________________________________________________ •__________________________________________________________ •3) ____________________________________________________________ ________________________ мұқият бол.
6 слайд
1 мысал: Өрнекті ықшамдаңдар:
2 4
)a ab
2 4
a b
2
;ab
4
6
16
)
9
a
б
b
4
6
16
9
a
b
2
3
4
.
3
a
b
2 мысал: Көбейткішті түбір таңбасының алдына
шығару:
) 81a a 81a 9 ;a
2
) 32б a
2
16 2a
2
16 2a 4 2;a
7 5
) 9в ab
6 4
9a a b b
6 4
9a a b b
3 2
3 .ab ab
6 слайд
1 мысал: Өрнекті ықшамдаңдар: 2 4 )a ab 2 4 a b 2 ;ab 4 6 16 ) 9 a б b 4 6 16 9 a b 2 3 4 . 3 a b 2 мысал: Көбейткішті түбір таңбасының алдына шығару: ) 81a a 81a 9 ;a 2 ) 32б a 2 16 2a 2 16 2a 4 2;a 7 5 ) 9в ab 6 4 9a a b b 6 4 9a a b b 3 2 3 .ab ab
7 слайд
3 мысал: Көбейткішті түбір таңбасының ішіне енгізу
) 2 2a 4 2 4 2
3
)
3
a b
б
a
2
9
3
a b
a
2
9
3
a b
a
3 .ab
8
7 слайд
3 мысал: Көбейткішті түбір таңбасының ішіне енгізу ) 2 2a 4 2 4 2 3 ) 3 a b б a 2 9 3 a b a 2 9 3 a b a 3 .ab 8
8 слайд
«Бірге ойлаймыз»
1.Көбейткішті түбір белгісінің алдына шығар.
А) = б) = в) =
2. Көбейткішті түбір белгісінің ішіне енгіз.
А)2 = б) 3 = в) 4 =
3.Бөлшектің бөліміндегі иррационалдықтан құтыл.
А) б) в)
12
75
72
3
5
2
21
1
23
5
35
4
8 слайд
«Бірге ойлаймыз» 1.Көбейткішті түбір белгісінің алдына шығар. А) = б) = в) = 2. Көбейткішті түбір белгісінің ішіне енгіз. А)2 = б) 3 = в) 4 = 3.Бөлшектің бөліміндегі иррационалдықтан құтыл. А) б) в) 12 75 72 3 5 2 21 1 23 5 35 4
9 слайд
«Фишбоун» тапсырмалары
1 тобы
45
18
23а
ух
1
А)
ә)
б)
2 тобы
62
24ва ава34
2
5
5
х
А)
ә)
б)
3 тобы
50
19
3 50
5
1
5
533
х
хА)
ә)
б)
9 слайд
«Фишбоун» тапсырмалары 1 тобы 45 18 23а ух 1 А) ә) б) 2 тобы 62 24ва ава34 2 5 5 х А) ә) б) 3 тобы 50 19 3 50 5 1 5 533 х хА) ә) б)
10 слайд
5
2
)а
2
18а
ух
ух
62)
3
ава ва
5
48
5
)5(5
2
х
х
25
13
)а 2
Жауаптары:
1 тобы:
ә)
б)
2 тобы:
ә)
3 тобы:
ә) б)3
б)
10 слайд
5 2 )а 2 18а ух ух 62) 3 ава ва 5 48 5 )5(5 2 х х 25 13 )а 2 Жауаптары: 1 тобы: ә) б) 2 тобы: ә) 3 тобы: ә) б)3 б)
11 слайд
Топпен жұмыс. Карточкамен жұмыс
Карточка 1
1. Есепте:
100
25
09,0
2. Салыстыр:
3. Өрнекті ықшамда:
1252 5240
baa 232
Карточка 2
1. Есепте:
2. Салыстыр:
3. Өрнекті ықшамда:
Карточка 3
1. Есепте:
2. Салыстыр:
3. Өрнекті ықшамда:
49 81 25,2
1642 5350
acac 4253
121 16 81,0
4223 2415
baa 5326
11 слайд
Топпен жұмыс. Карточкамен жұмыс Карточка 1 1. Есепте: 100 25 09,0 2. Салыстыр: 3. Өрнекті ықшамда: 1252 5240 baa 232 Карточка 2 1. Есепте: 2. Салыстыр: 3. Өрнекті ықшамда: Карточка 3 1. Есепте: 2. Салыстыр: 3. Өрнекті ықшамда: 49 81 25,2 1642 5350 acac 4253 121 16 81,0 4223 2415 baa 5326
12 слайд
12
СЕРГІТУ
СӘТІ
12 слайд
12 СЕРГІТУ СӘТІ
13 слайд
Берілген алгебралық өрнекті бөлшектің бөлімінде
квадрат түбір таңбасы болмайтындай етіп
түрлендіру:
1
)
2
a
Бөлшектің бөлімін және алымын бір мезгілде
нөлден өзгеше санға немесе өрнекке көбейтсек,
бөлшектің мәні өзгермейді
1
2
1 2
2 2
2
2
2
2
.
2
1
)
3 2
б
1 3 2
3 2 3 2
2 2
3 2
3 2
3 2
3 2
3 2.
23
1
)
б
13 слайд
Берілген алгебралық өрнекті бөлшектің бөлімінде квадрат түбір таңбасы болмайтындай етіп түрлендіру: 1 ) 2 a Бөлшектің бөлімін және алымын бір мезгілде нөлден өзгеше санға немесе өрнекке көбейтсек, бөлшектің мәні өзгермейді 1 2 1 2 2 2 2 2 2 2 . 2 1 ) 3 2 б 1 3 2 3 2 3 2 2 2 3 2 3 2 3 2 3 2 3 2. 23 1 ) б
14 слайд
- егер бөлшектің бөлімі түрінде болса, онда бөлшектің
алымын да, бөлімін де -ға көбейту керек
Егер алгебралық бөлшектің бөлімінде түбір таңбасы
тұратын болса, онда
бөлшектің бөлімі иррационалдықты құрайды
деп айтады.
Өрнекті бөлшектің бөлімінде түбір таңбасы
болмайтындай етіп түрлендіруді
бөлшектің бөлімін иррационалдықтан құтқару
деп атайды.
-егер бөлшектің бөлімі немесе түрде болса,
онда бөлшектің бөлімін де, алымын да сәйкесінше
немесе (түйіндес өрнекке)
көбейту керек
а
аb аb
аb аb
а
14 слайд
- егер бөлшектің бөлімі түрінде болса, онда бөлшектің алымын да, бөлімін де -ға көбейту керек Егер алгебралық бөлшектің бөлімінде түбір таңбасы тұратын болса, онда бөлшектің бөлімі иррационалдықты құрайды деп айтады. Өрнекті бөлшектің бөлімінде түбір таңбасы болмайтындай етіп түрлендіруді бөлшектің бөлімін иррационалдықтан құтқару деп атайды. -егер бөлшектің бөлімі немесе түрде болса, онда бөлшектің бөлімін де, алымын да сәйкесінше немесе (түйіндес өрнекке) көбейту керек а аb аb аb аb а
15 слайд
Өрнекті ықшамдау: .
35
4
57
2
7
7
7
7
)1
77
77
7
77
;7
57
2
)2
5757
572
22
57
572
57
572
2
572
;57
35
4
)3
3535
354
22
35
354
35
354
2
354
;352
)35(2)57(7)4 3252577
.325
15 слайд
Өрнекті ықшамдау: . 35 4 57 2 7 7 7 7 )1 77 77 7 77 ;7 57 2 )2 5757 572 22 57 572 57 572 2 572 ;57 35 4 )3 3535 354 22 35 354 35 354 2 354 ;352 )35(2)57(7)4 3252577 .325
16 слайд
Үй тапсырмасы:
•Тест бойынша қатемен жұмыс.
•Оқулықтағы немесе мұғалім берген
қосымша тапсырмаларды орындап келу.
•Жіберген қателерді талдай отырып,
1-тарауды қайталап келу.
16 слайд
Үй тапсырмасы: •Тест бойынша қатемен жұмыс. •Оқулықтағы немесе мұғалім берген қосымша тапсырмаларды орындап келу. •Жіберген қателерді талдай отырып, 1-тарауды қайталап келу.
17 слайд
17
НАЗАРЛАРЫҢЫЗҒА
РАХМЕТ!
17 слайд
17 НАЗАРЛАРЫҢЫЗҒА РАХМЕТ!
