Сферамен жазықтықтың өзара орналасуы

1 слайд

2 слайд
1. Білім алушыларға сфера мен жазықтықтың өзара орналасуының түрлерін меңгерту, есеп шығару дағдыларын қалыптастыру. 2. Білім алушыларға ақпараттық технологияны қолдана отырып, өзіне өзі талдау жасау, түзету әрекеттерін қолдану және деңгейлік тапсырмалар орындату арқылы шығармашылығын дамыту. 3. Білім алушыларды математика және информатика пәндеріне деген танымдық қызығушылығын арттыру, ақпараттық тәрбиеге баулу, ұжымдық жұмысқа тәрбиелеу.

3 слайд
1. Үй тапсырмасын тексереміз / бақылау 1. Үй тапсырмасын тексереміз / бақылау сұрақтары, тесттік тапсырма/.сұрақтары, тесттік тапсырма/. 2. Жаңа білімді меңгереміз.2. Жаңа білімді меңгереміз. 3. Топтарға бөлініп проблемалық іздеу 3. Топтарға бөлініп проблемалық іздеу жұмыстарын жүргіземіз.жұмыстарын жүргіземіз. 4. Қорытындылай отырып, бағалаймыз.4. Қорытындылай отырып, бағалаймыз.

4 слайд

5 слайд
Шар ма, әлде Шар ма, әлде сфера ма?сфера ма?

6 слайд
Шардың анықтамасы

7 слайд
Шардың анықтамасы Шар деп берілген нүктеден берілген қашықтықтан артық емес қашықтықта жататын кеңістіктің барлық нүктелерінен тұратын денені айтамыз

8 слайд
Сфераның анықтамасы

9 слайд
Сферан ың анықтамасы Сфера деп берілген нүктеден берілген қашықтықта орналасқан кеңістіктің барлық нүктелерін құрайтын бетті айтамыз.

10 слайд
А мен В нүктелері шарда жатыр. АВ кесіндісінің кез келген нүктесі шарда жата ма?

11 слайд

12 слайд
Тестің дұрыс жауаптары 1. А 2. В 3. Б 4. А 5. Б 6. В 7. Б 8. А

13 слайд
Жаңа материалды түсіндіру кезеңі Жаңа білімді игермес бұрын, біз тақырыпты өзіміз анықтауды іске асырайық. Ол үшін экрандағы 3-сызбаға назар аударайық.

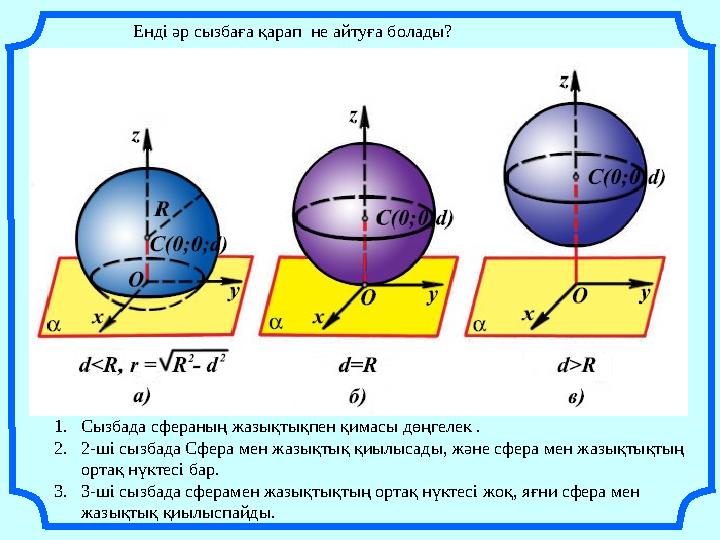
14 слайд
Енді әр сызбаға қарап не айтуға болады? 1. Сызбада сфераның жазықтықпен қимасы дөңгелек . 2. 2-ші сызбада Сфера мен жазықтық қиылысады, және сфера мен жазықтықтың ортақ нүктесі бар. 3. 3-ші сызбада сферамен жазықтықтың ортақ нүктесі жоқ, яғни сфера мен жазықтық қиылыспайды.

15 слайд
Мүмкін енді айтарсыңдар бүгінгі тақырып қандай?

16 слайд

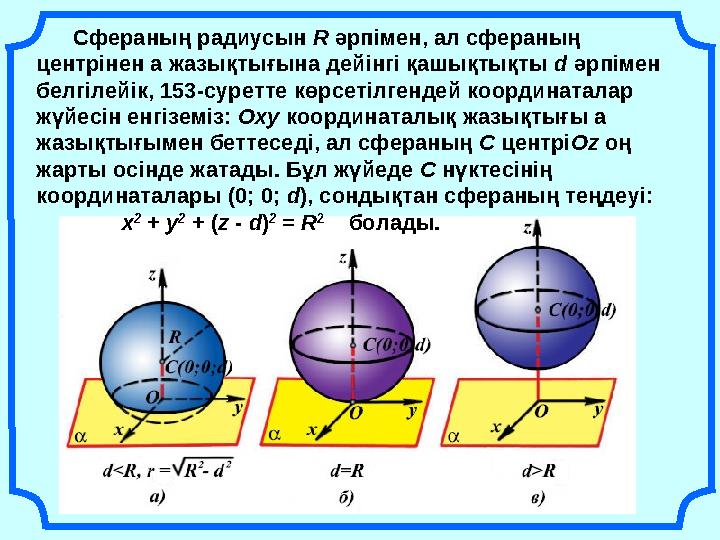
17 слайд
      Сфераның радиусын R әрпімен, ал сфераның центрінен a жазықтығына дейінгі қашықтықты d әрпімен белгілейік, 153-суретте көрсетілгендей координаталар жүйесін енгіземіз: Оху координаталық жазықтығы a жазықтығымен беттеседі, ал сфераның С центрі Оz оң жарты осінде жатады. Бұл жүйеде С нүктесінің координаталары (0; 0; d ), сондықтан сфераның теңдеуі: х 2 + у 2 + ( z - d ) 2 = R 2 болады.

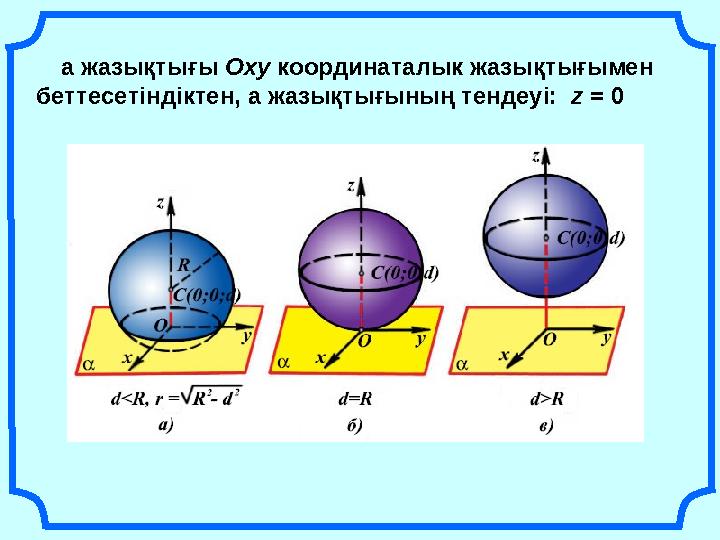
18 слайд
     a жазықтығы Охy координаталык жазықтығымен беттесетіндіктен, a жазықтығының тендеуі: z = 0

19 слайд
     Егер қандай да бір М ( х ; у ; z ) нүктесінің координаталары екі теңдеуді де қанағаттандырса, онда М нүктесі а жазықтығында да, сферада да жатады, яғни М нүктесі жазықтық пен сфераның ортақ нүктесі болады. Егер бұл екі теңдеу жүйесінің шешімі жоқ болса, онда сфера мен жазықтықтың ортақ нүктесі жоқ. Сонымен, сфера мен жазықтықтың өзара орналасу мәселесі теңдеулер жүйесін зерттеуге келіп тіреледі

20 слайд
     z = 0 -ді екінші теңдеуге қойсақ , мына теңдеуді аламыз. х 2 + у 2 = R 2 – d 2 .

21 слайд
Түсінікті болса , c фера мен жазықтықтың өзара орналасуын, сфераның радиусы мен сфера центрінен жазықтыққа дейінгі қашықтықтың арасындағы қатысқа байланысты үш жағдай болуы мүмкіндігіне зерттеу жұмыстарын жүргізейік. Әр топқа 10 минуттан уақыт беріледі.

22 слайд

23 слайд
Ендеше, 1-топқа d < R болса, онда қандай тұжырым жасауға болады ? 2 -топқа d = R болса, онда қандай тұжырым жасауға болады ? 3-топқа d > R болса, онда қандай тұжырым жасауға болады ?

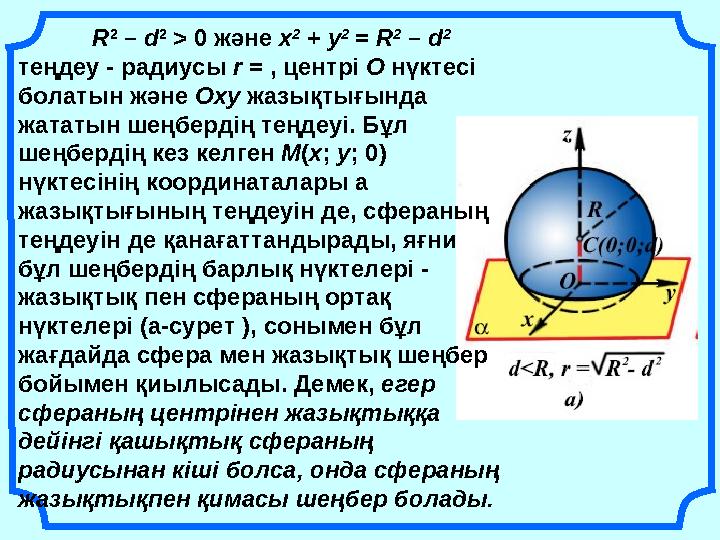
24 слайд
           R 2 – d 2 > 0 және х 2 + у 2 = R 2 – d 2 теңдеу - радиусы r = , центрі О нүктесі болатын және Оху жазықтығында жататын шеңбердің теңдеуі. Бұл шеңбердің кез келген М ( х ; у ; 0) нүктесінің координаталары a жазықтығының теңдеуін де, сфераның теңдеуін де қанағаттандырады, яғни бұл шеңбердің барлық нүктелері - жазықтық пен сфераның ортақ нүктелері (а-сурет ), сонымен бұл жағдайда сфера мен жазықтық шеңбер бойымен қиылысады. Демек, егер сфераның центрінен жазықтыққа дейінгі қашықтық сфераның радиусынан кіші болса, онда сфераның жазықтықпен қимасы шеңбер болады.

25 слайд
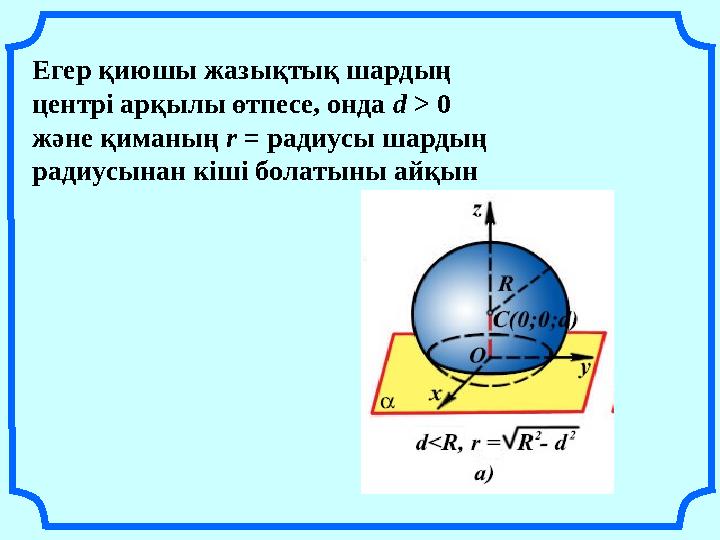
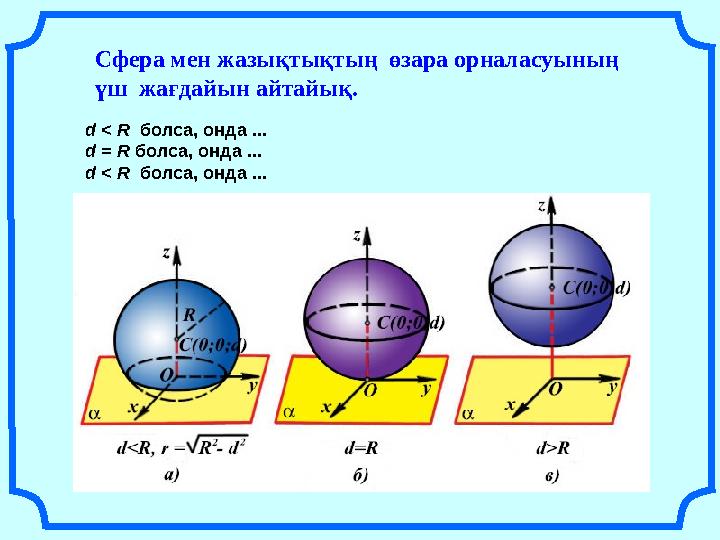
Шардың жазықтықпен қимасы дөңгелек болатыны түсінікті. Егер қиюшы жазықтық шардың центрі арқылы өтсе, онда d = 0 болады да, қимада радиусы R дөңгелек шығады, бұл дөңгелектің радиусы шардың радиусына тең. Мұндай дөңгелек шардың үлкен дөңгелегі деп аталады

26 слайд
Егер қиюшы жазықтық шардың центрі арқылы өтпесе, онда d > 0 және қиманың r = радиусы шардың радиусынан кіші болатыны айқын

27 слайд
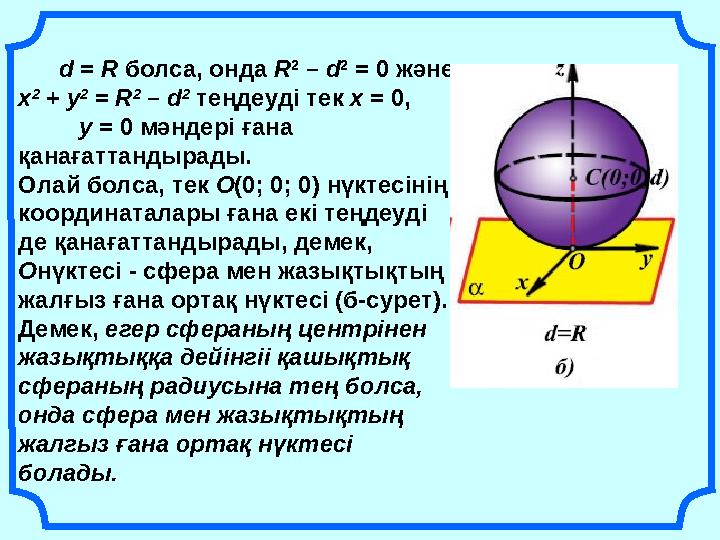
       d = R болса, онда R 2 – d 2 = 0 және х 2 + у 2 = R 2 – d 2 теңдеуді тек х = 0, у = 0 мәндері ғана қанағаттандырады. Олай болса, тек О (0; 0; 0) нүктесінің координаталары ғана екі теңдеуді де қанағаттандырады, демек, О нүктесі - сфера мен жазықтықтың жалғыз ғана ортақ нүктесі (б-сурет). Демек, егер сфераның центрінен жазықтыққа дейінгіі қашықтық сфераның радиусына тең болса, онда сфера мен жазықтықтың жалгыз ғана ортақ нүктесі болады.

28 слайд
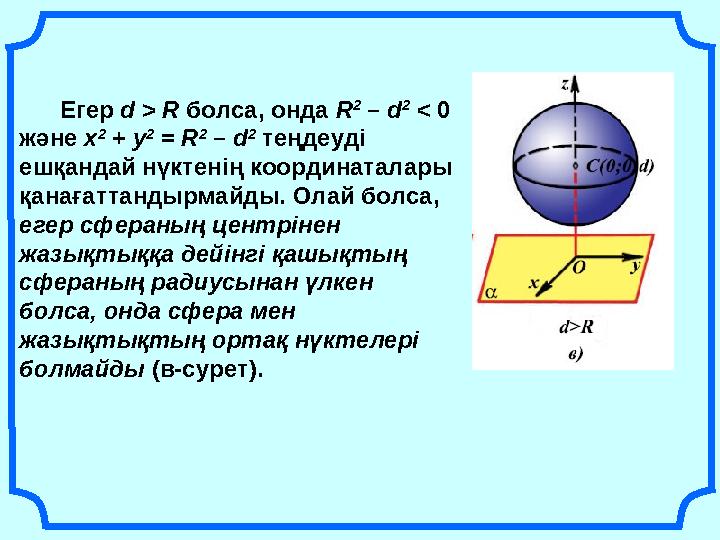
       Егер d > R болса, онда R 2 – d 2 < 0 және х 2 + у 2 = R 2 – d 2 теңдеуді ешқандай нүктенің координаталары қанағаттандырмайды. Олай болса, егер сфераның центрінен жазықтыққа дейінгі қашықтың сфераның радиусынан үлкен болса, онда сфера мен жазықтықтың ортақ нүктелері болмайды (в-сурет).

29 слайд
Сабақты қорытындылай отырып, деңгейлік тапсырмаларды орындайық.

30 слайд
1.Сфераның үш нүктесінің бір түзудің бойында жатуы мүмкін бе? Өз ойларыңды айтыңдар. 2.Шеңбер берілген. Осы шеңберді қамтитын қанша сфера жүргізуге болады. І-деңгейлік тапсырма

31 слайд
3. а) Берілген екі нүкте арқылы; ә) берілген үш нүкте арқылы әртүрлі қанша сфера жүргізуге болады? 4. Радиусы 15-ке тең сфераның центрінен 9-ға тең қашықтықта хорда өтеді. Хорданың ұзындығы қншаға тең? 5. Ұзындығы 12 см хорда сфераның центрінен 6см қашықтықта өтеді. Сфераның радиусын табыңдар. ІІ-деңгейлік тапсырма

32 слайд
6. Есеп №580 Радиусы 41 дм шар центрінен 9 дм қашықтықта жазықтық пен қиылған. Қиманың ауданын табыңдар. 7. Есеп №586 ОН кесіндісі-ОАВС- тетраэдрдің биіктігі. Егер R=6 дм, OH= 60 см болса, онда центрі О, радиусы R болатын сфера мен АВС жазықтығының орналасуын анықтаңдар. ІІІ-деңгейлік тапсырма

33 слайд
Сфера мен жазықтықтың өзара орналасуының үш жағдайын айтайық. d < R болса, онда ... d = R болса, онда ... d < R болса, онда ...

34 слайд
Сфера мен жазықтықтың өзара орналасуы. №586 есептің ә,б,в шығаруҮйге тапсырма