Материалдар / Үшбұрыштар

Үшбұрыштар

Материал туралы қысқаша түсінік

математика пәнінің мұғалімдеріне

Баделқан Қастер

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

03 Қараша 2019

428

0 рет жүктелген

Геометрия Презентация 7 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 15

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд
 Анықтама:  Үшбұрыш элементтері  Үшбұрыштың түрлері қабырғалары бойынша  Үшбұрыштың түрлері бұрыштары бойынша  Үшбұрыштар теңдігі  Подобие треугольников  Үшбұрыштың ауданы  Синус және косинус теоремасы  Пифагор теоремасы  Пифагор теоремасының дәлелдемесі  Тапсырма

2 слайд

 Анықтама:  Үшбұрыш элементтері  Үшбұрыштың түрлері қабырғалары бойынша  Үшбұрыштың түрлері бұрыштары бойынша  Үшбұрыштар теңдігі  Подобие треугольников  Үшбұрыштың ауданы  Синус және косинус теоремасы  Пифагор теоремасы  Пифагор теоремасының дәлелдемесі  Тапсырма

3 слайд
 Ең қарапайым көпбұрыш, үш нүктеден, үш қабырғадан және үш бұрыштан  Бір түзу бойында жатпайтын үш нүктені қосатын кесінділер шектейтін жазықтық бөлігі Үшбұрыш

3 слайд

 Ең қарапайым көпбұрыш, үш нүктеден, үш қабырғадан және үш бұрыштан  Бір түзу бойында жатпайтын үш нүктені қосатын кесінділер шектейтін жазықтық бөлігі Үшбұрыш

4 слайд
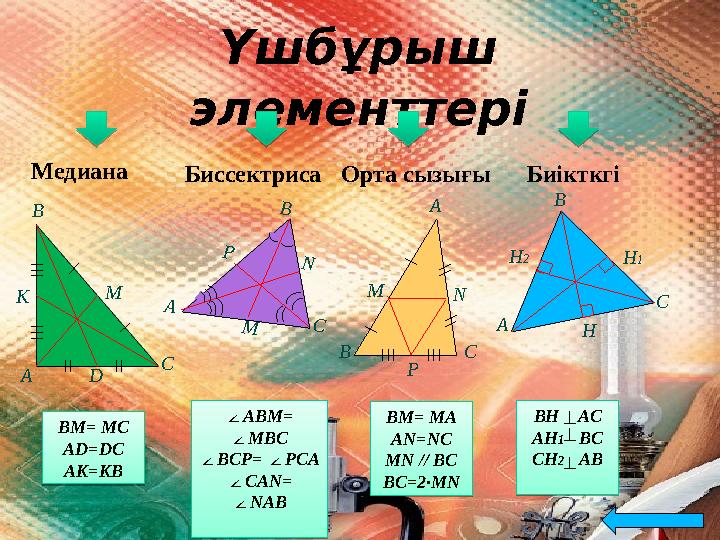
Үшбұрыш элементтері Медиана Биікткгі Биссектриса Орта сызы ғы A B C HBA B C M A B CM N BM= MC AD=DC AK=KB BM= MA AN=NC MN // BC BC=2·MN BH AC AH 1 BC CH 2 ABA B CM P DK H 2 H 1 N P ∠ ABM= ∠ MBC ∠ BCP= ∠ PCA ∠ CAN= ∠ NAB BM= MC AD=DC AK=KB BM= MA AN=NC MN // BC BC=2·MN BH AC AH 1 BC CH 2 AB ∠ ABM= ∠ MBC ∠ BCP= ∠ PCA ∠ CAN= ∠ NAB

4 слайд

Үшбұрыш элементтері Медиана Биікткгі Биссектриса Орта сызы ғы A B C HBA B C M A B CM N BM= MC AD=DC AK=KB BM= MA AN=NC MN // BC BC=2·MN BH AC AH 1 BC CH 2 ABA B CM P DK H 2 H 1 N P ∠ ABM= ∠ MBC ∠ BCP= ∠ PCA ∠ CAN= ∠ NAB BM= MC AD=DC AK=KB BM= MA AN=NC MN // BC BC=2·MN BH AC AH 1 BC CH 2 AB ∠ ABM= ∠ MBC ∠ BCP= ∠ PCA ∠ CAN= ∠ NAB

5 слайд
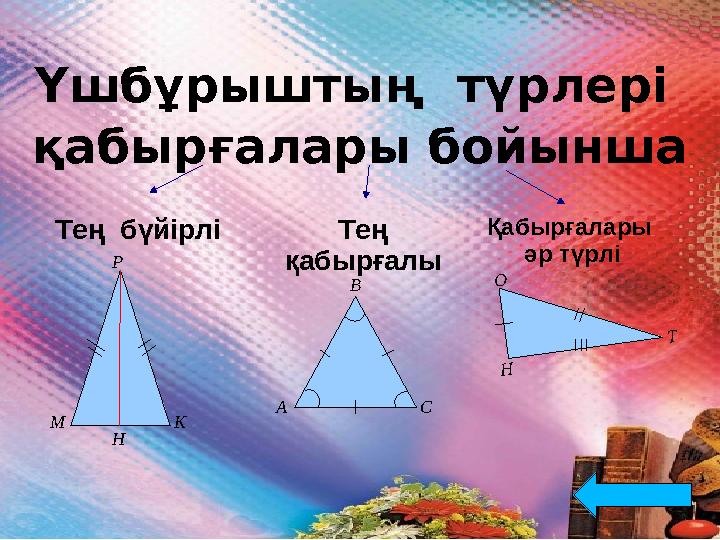
Үшбұрыштың түрлері қабырғалары бойынша Тең қабырғалыТең бүйірлі Қабырғалары әр түрліН О Т М Р К H А В С

5 слайд

Үшбұрыштың түрлері қабырғалары бойынша Тең қабырғалыТең бүйірлі Қабырғалары әр түрліН О Т М Р К H А В С

6 слайд
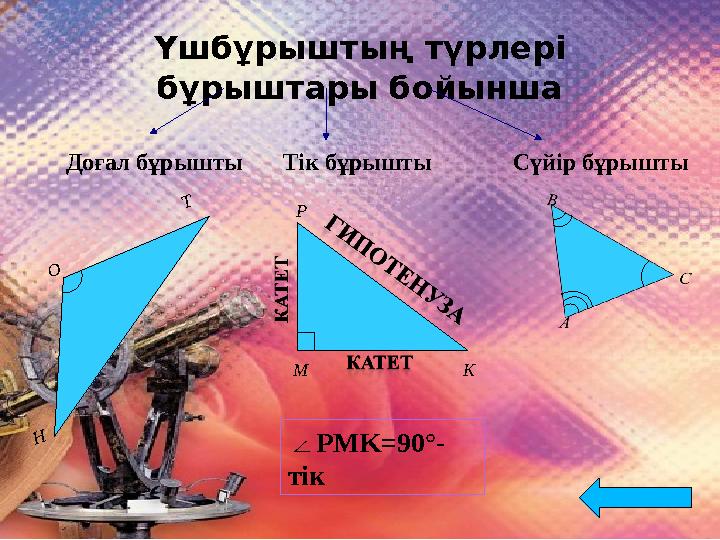
Үшбұрыштың түрлері бұрыштары бойынша Тік бұрыштыДоғал бұрыштыН О Т Сүйір бұрышты ∠ PMK=90° - тік М Р К

6 слайд

Үшбұрыштың түрлері бұрыштары бойынша Тік бұрыштыДоғал бұрыштыН О Т Сүйір бұрышты ∠ PMK=90° - тік М Р К

7 слайд
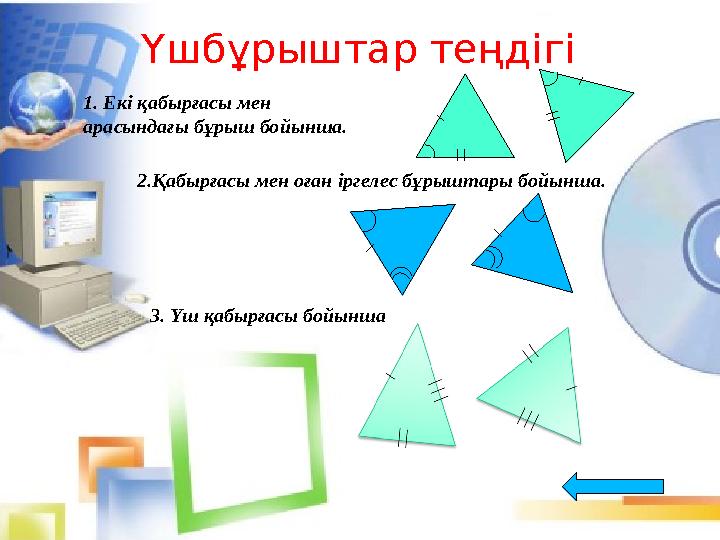
Үшбұрыштар теңдігі 2.Қабырғасы мен оған іргелес бұрыштары бойынша. 3. Үш қабырғасы бойынша1. Екі қабырғасы мен арасындағы бұрыш бойынша.

7 слайд

Үшбұрыштар теңдігі 2.Қабырғасы мен оған іргелес бұрыштары бойынша. 3. Үш қабырғасы бойынша1. Екі қабырғасы мен арасындағы бұрыш бойынша.

8 слайд
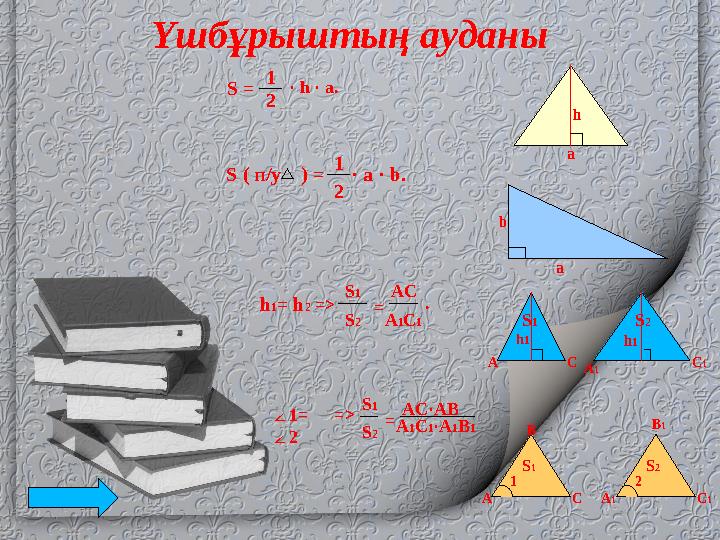
21 S = · h · a.Үшбұрыштың ауданы S ( п/у ) = 1 2 · a · b. ab h 1 = h 2 => S 1 S 2 = AC A 1 C 1 . ∠ 1= ∠ 2 => S 1 S 2 = AC·AB A 1 C 1 ·A 1 B 1 1 2S 1 S 2 A B C C 1A 1 B 1h 1 h 1S 1 S 2 A C A 1 C 1h a

8 слайд

21 S = · h · a.Үшбұрыштың ауданы S ( п/у ) = 1 2 · a · b. ab h 1 = h 2 => S 1 S 2 = AC A 1 C 1 . ∠ 1= ∠ 2 => S 1 S 2 = AC·AB A 1 C 1 ·A 1 B 1 1 2S 1 S 2 A B C C 1A 1 B 1h 1 h 1S 1 S 2 A C A 1 C 1h a

9 слайд
Синус және косинус теоремасы Синустар теоремасы a sin a = b sin b = c sin c = 2·R. a a b b cc R Косинустар теоремасы a 2 b 2 = + c 2 -2·b·c·cos a.

9 слайд

Синус және косинус теоремасы Синустар теоремасы a sin a = b sin b = c sin c = 2·R. a a b b cc R Косинустар теоремасы a 2 b 2 = + c 2 -2·b·c·cos a.

10 слайд
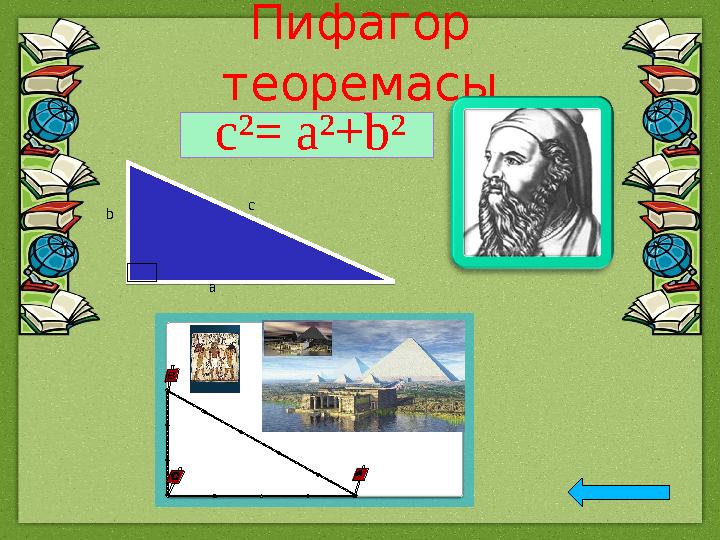
Пифагор теоремасыВ ab cc² = а ² + b²

10 слайд

Пифагор теоремасыВ ab cc² = а ² + b²

11 слайд
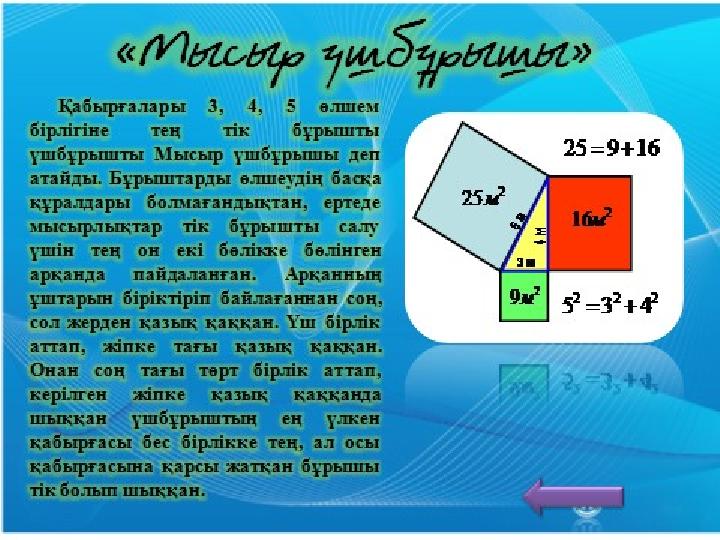
Пифагор теоремасының дәлелдемесі Мұндағы : а ,b- катеты, с-гипотенуза. Дәлелдеу керек : a 2 +b 2 =c 2 . Дәлелдеуі : (a+b). S 1 =(a+b) 2 S 2 =4(1/2ab)+c 2 S 1 =S 2 . (a+b) 2 =4(1/2ab)+c 2 а 2 +2ab+b 2 =2ab+c 2 а 2 +b 2 =c 2

11 слайд

Пифагор теоремасының дәлелдемесі Мұндағы : а ,b- катеты, с-гипотенуза. Дәлелдеу керек : a 2 +b 2 =c 2 . Дәлелдеуі : (a+b). S 1 =(a+b) 2 S 2 =4(1/2ab)+c 2 S 1 =S 2 . (a+b) 2 =4(1/2ab)+c 2 а 2 +2ab+b 2 =2ab+c 2 а 2 +b 2 =c 2

12 слайд

13 слайд
Вот задача индийского математика 12в. Бхаскары На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки . Осталось три фута всего от ствола, прошу тебя, скоро теперь мне скажи: у тополя как велика высота? Задача Решение: По теореме Пифагора находим С D : CD = 3 + 4 = 9 + 16 =25 => CD= 5. Высота тополя равна: CB+CA. Т.к. CD=CB => AB=AC+CD= 3 + 5 = 8. Ответ: высота тополя 8 футов. 2 22

13 слайд

Вот задача индийского математика 12в. Бхаскары На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки . Осталось три фута всего от ствола, прошу тебя, скоро теперь мне скажи: у тополя как велика высота? Задача Решение: По теореме Пифагора находим С D : CD = 3 + 4 = 9 + 16 =25 => CD= 5. Высота тополя равна: CB+CA. Т.к. CD=CB => AB=AC+CD= 3 + 5 = 8. Ответ: высота тополя 8 футов. 2 22

14 слайд
Назарларыңызға рахмет!

14 слайд

Назарларыңызға рахмет!