Материалдар / Тік бұрышты үшбұрыштар теңдігінің белгілері Тікбұрышты үшбұрыштың қасиеттері 7 сынып геометрия сабак жоспары

Тік бұрышты үшбұрыштар теңдігінің белгілері Тікбұрышты үшбұрыштың қасиеттері 7 сынып геометрия сабак жоспары

Материал туралы қысқаша түсінік

Тік бұрышты үшбұрыштардың теңдік белгілерін дәлелдейді және теңдік белгілерін есептер шығаруға қолдана біледі. Тікбұрышты үшбұрыштың қасиеттерін білу, бекіту және оларды пайдаланып есеп шығаруда жеке жұмыс жасай білу дағдыларын қалыптастыру

Зейнолда Көшкенбек

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

21 Желтоқсан 2020

757

2 рет жүктелген

Геометрия Сабақ жоспары 7 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 12

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Үшбұрыштардың теңдігінің Үшбұрыштардың теңдігінің үшінші белгісіүшінші белгісі 7.3.2.4 үшбұрыштар теңдігінің белгілерін біледі және 7.3.2.4 үшбұрыштар теңдігінің белгілерін біледі және дәлелдейді;дәлелдейді; 7.3.3.4 үшбұрыштар теңдігінің белгілерін қолданып, 7.3.3.4 үшбұрыштар теңдігінің белгілерін қолданып, есептеуге және дәлелдеуге есептерді шығарады;есептеуге және дәлелдеуге есептерді шығарады;

1 слайд

Үшбұрыштардың теңдігінің Үшбұрыштардың теңдігінің үшінші белгісіүшінші белгісі 7.3.2.4 үшбұрыштар теңдігінің белгілерін біледі және 7.3.2.4 үшбұрыштар теңдігінің белгілерін біледі және дәлелдейді;дәлелдейді; 7.3.3.4 үшбұрыштар теңдігінің белгілерін қолданып, 7.3.3.4 үшбұрыштар теңдігінің белгілерін қолданып, есептеуге және дәлелдеуге есептерді шығарады;есептеуге және дәлелдеуге есептерді шығарады;

2 слайд
ҚАЙТАЛАУҚАЙТАЛАУ

2 слайд

ҚАЙТАЛАУҚАЙТАЛАУ

3 слайд
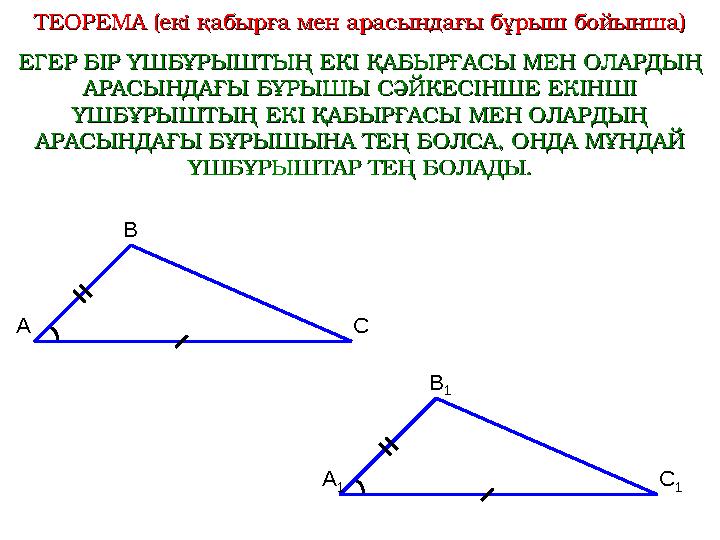
ТЕОРЕМА (екі қабырға мен арасындағы бұрыш бойынша)ТЕОРЕМА (екі қабырға мен арасындағы бұрыш бойынша) ЕГЕР БІР ҮШБҰРЫШТЫҢ ЕКІ ҚАБЫРҒАСЫ МЕН ОЛАРДЫҢ ЕГЕР БІР ҮШБҰРЫШТЫҢ ЕКІ ҚАБЫРҒАСЫ МЕН ОЛАРДЫҢ АРАСЫНДАҒЫ БҰРЫШЫ СӘЙКЕСІНШЕ ЕКІНШІ АРАСЫНДАҒЫ БҰРЫШЫ СӘЙКЕСІНШЕ ЕКІНШІ ҮШБҰРЫШТЫҢ ЕКІ ҚАБЫРҒАСЫ МЕН ОЛАРДЫҢ ҮШБҰРЫШТЫҢ ЕКІ ҚАБЫРҒАСЫ МЕН ОЛАРДЫҢ АРАСЫНДАҒЫ БҰРЫШЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ АРАСЫНДАҒЫ БҰРЫШЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ.ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ. A В С A 1 В 1 С 1

3 слайд

ТЕОРЕМА (екі қабырға мен арасындағы бұрыш бойынша)ТЕОРЕМА (екі қабырға мен арасындағы бұрыш бойынша) ЕГЕР БІР ҮШБҰРЫШТЫҢ ЕКІ ҚАБЫРҒАСЫ МЕН ОЛАРДЫҢ ЕГЕР БІР ҮШБҰРЫШТЫҢ ЕКІ ҚАБЫРҒАСЫ МЕН ОЛАРДЫҢ АРАСЫНДАҒЫ БҰРЫШЫ СӘЙКЕСІНШЕ ЕКІНШІ АРАСЫНДАҒЫ БҰРЫШЫ СӘЙКЕСІНШЕ ЕКІНШІ ҮШБҰРЫШТЫҢ ЕКІ ҚАБЫРҒАСЫ МЕН ОЛАРДЫҢ ҮШБҰРЫШТЫҢ ЕКІ ҚАБЫРҒАСЫ МЕН ОЛАРДЫҢ АРАСЫНДАҒЫ БҰРЫШЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ АРАСЫНДАҒЫ БҰРЫШЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ.ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ. A В С A 1 В 1 С 1

4 слайд
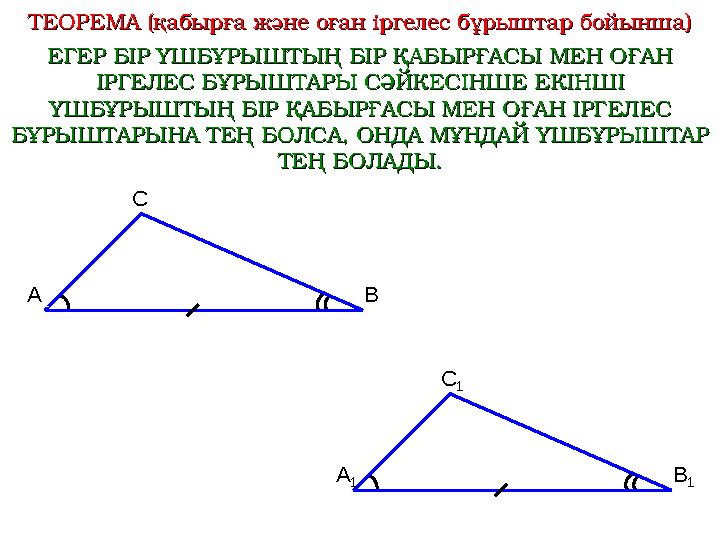
ТЕОРЕМА (қабырға және оған іргелес бұрыштар бойынша)ТЕОРЕМА (қабырға және оған іргелес бұрыштар бойынша) ЕГЕР БІР ҮШБҰРЫШТЫҢ БІР ҚАБЫРҒАСЫ МЕН ОҒАН ЕГЕР БІР ҮШБҰРЫШТЫҢ БІР ҚАБЫРҒАСЫ МЕН ОҒАН ІРГЕЛЕС БҰРЫШТАРЫ СӘЙКЕСІНШЕ ЕКІНШІ ІРГЕЛЕС БҰРЫШТАРЫ СӘЙКЕСІНШЕ ЕКІНШІ ҮШБҰРЫШТЫҢ БІР ҚАБЫРҒАСЫ МЕН ОҒАН ІРГЕЛЕС ҮШБҰРЫШТЫҢ БІР ҚАБЫРҒАСЫ МЕН ОҒАН ІРГЕЛЕС БҰРЫШТАРЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ ҮШБҰРЫШТАР БҰРЫШТАРЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ.ТЕҢ БОЛАДЫ. A 1 С 1 В 1 A 1 С 1 В 1

4 слайд

ТЕОРЕМА (қабырға және оған іргелес бұрыштар бойынша)ТЕОРЕМА (қабырға және оған іргелес бұрыштар бойынша) ЕГЕР БІР ҮШБҰРЫШТЫҢ БІР ҚАБЫРҒАСЫ МЕН ОҒАН ЕГЕР БІР ҮШБҰРЫШТЫҢ БІР ҚАБЫРҒАСЫ МЕН ОҒАН ІРГЕЛЕС БҰРЫШТАРЫ СӘЙКЕСІНШЕ ЕКІНШІ ІРГЕЛЕС БҰРЫШТАРЫ СӘЙКЕСІНШЕ ЕКІНШІ ҮШБҰРЫШТЫҢ БІР ҚАБЫРҒАСЫ МЕН ОҒАН ІРГЕЛЕС ҮШБҰРЫШТЫҢ БІР ҚАБЫРҒАСЫ МЕН ОҒАН ІРГЕЛЕС БҰРЫШТАРЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ ҮШБҰРЫШТАР БҰРЫШТАРЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ.ТЕҢ БОЛАДЫ. A 1 С 1 В 1 A 1 С 1 В 1

5 слайд
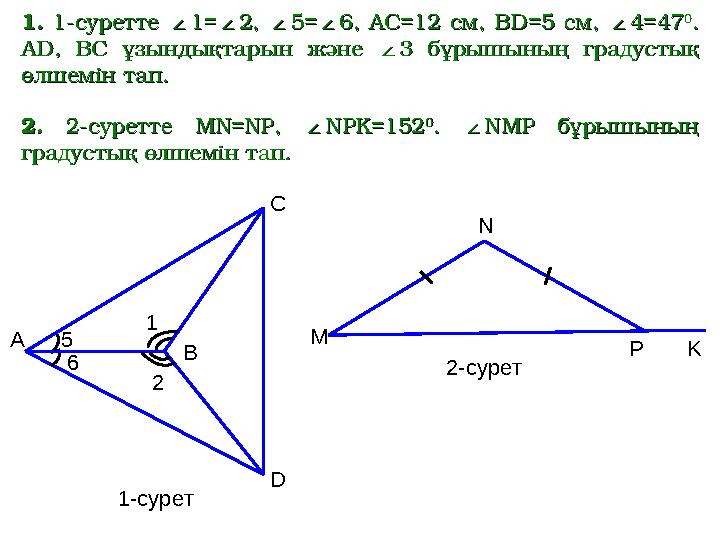
DА С В5 6 1- сурет1.1. 1-суретте 1-суретте ∠1=∠2, ∠∠1=∠2, ∠ 55 =∠=∠ 6, АС6, АС =12=12 см, В см, В D=D= 5 см5 см , , ∠4∠4 == 4747 00 . . АА DD , ВС ұзындықтарын және , ВС ұзындықтарын және ∠∠ 3 бұрышының градустық 3 бұрышының градустық өлшемін тап.өлшемін тап. 2.2. 2-суретте 2-суретте MN=NP, ∠NPK=152MN=NP, ∠NPK=152 00 . ∠NMP. ∠NMP бұрышының бұрышының градустық өлшемін тап.градустық өлшемін тап. M P 2 - сурет KN 1 2

5 слайд

DА С В5 6 1- сурет1.1. 1-суретте 1-суретте ∠1=∠2, ∠∠1=∠2, ∠ 55 =∠=∠ 6, АС6, АС =12=12 см, В см, В D=D= 5 см5 см , , ∠4∠4 == 4747 00 . . АА DD , ВС ұзындықтарын және , ВС ұзындықтарын және ∠∠ 3 бұрышының градустық 3 бұрышының градустық өлшемін тап.өлшемін тап. 2.2. 2-суретте 2-суретте MN=NP, ∠NPK=152MN=NP, ∠NPK=152 00 . ∠NMP. ∠NMP бұрышының бұрышының градустық өлшемін тап.градустық өлшемін тап. M P 2 - сурет KN 1 2

6 слайд
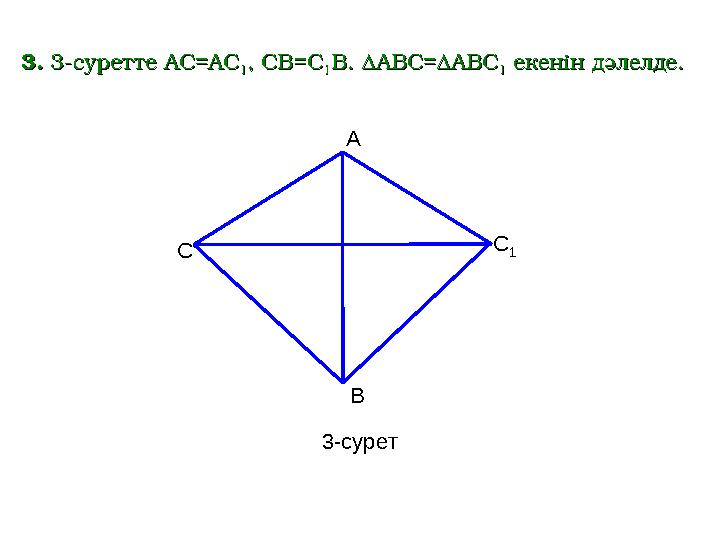
C A С 1 B 3- сурет33 .. 33 -суретте-суретте AC=AC AC=AC 11 , CB=C, CB=C 11 B.B. ∆ABC=∆ABC∆ABC=∆ABC 11 екенін дәлелде.екенін дәлелде.

6 слайд

C A С 1 B 3- сурет33 .. 33 -суретте-суретте AC=AC AC=AC 11 , CB=C, CB=C 11 B.B. ∆ABC=∆ABC∆ABC=∆ABC 11 екенін дәлелде.екенін дәлелде.

7 слайд
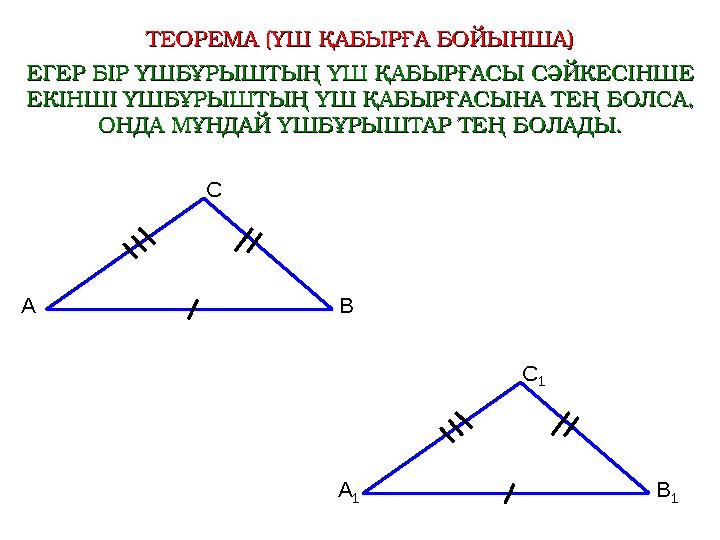
ТЕОРЕМА (ҮШ ҚАБЫРҒА БОЙЫНША)ТЕОРЕМА (ҮШ ҚАБЫРҒА БОЙЫНША) ЕГЕР БІР ҮШБҰРЫШТЫҢ ҮШ ҚАБЫРҒАСЫ СӘЙКЕСІНШЕ ЕГЕР БІР ҮШБҰРЫШТЫҢ ҮШ ҚАБЫРҒАСЫ СӘЙКЕСІНШЕ ЕКІНШІ ҮШБҰРЫШТЫҢ ҮШ ҚАБЫРҒАСЫНА ТЕҢ БОЛСА, ЕКІНШІ ҮШБҰРЫШТЫҢ ҮШ ҚАБЫРҒАСЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ.ОНДА МҰНДАЙ ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ. A С В A 1 С 1 В 1

7 слайд

ТЕОРЕМА (ҮШ ҚАБЫРҒА БОЙЫНША)ТЕОРЕМА (ҮШ ҚАБЫРҒА БОЙЫНША) ЕГЕР БІР ҮШБҰРЫШТЫҢ ҮШ ҚАБЫРҒАСЫ СӘЙКЕСІНШЕ ЕГЕР БІР ҮШБҰРЫШТЫҢ ҮШ ҚАБЫРҒАСЫ СӘЙКЕСІНШЕ ЕКІНШІ ҮШБҰРЫШТЫҢ ҮШ ҚАБЫРҒАСЫНА ТЕҢ БОЛСА, ЕКІНШІ ҮШБҰРЫШТЫҢ ҮШ ҚАБЫРҒАСЫНА ТЕҢ БОЛСА, ОНДА МҰНДАЙ ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ.ОНДА МҰНДАЙ ҮШБҰРЫШТАР ТЕҢ БОЛАДЫ. A С В A 1 С 1 В 1

8 слайд
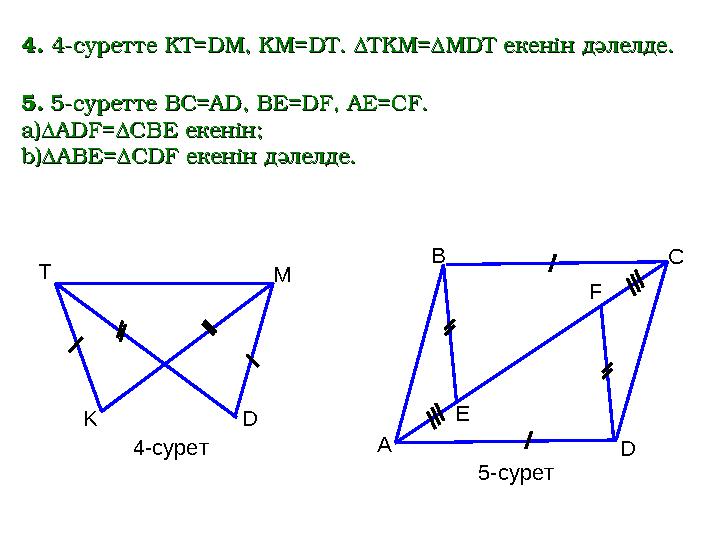
44 . . 44 -суретте-суретте KT=DM, KM=DT. ∆TKM=∆MDT KT=DM, KM=DT. ∆TKM=∆MDT екенін дәлелде.екенін дәлелде. T M K D 4- сурет55 .. 55 -суретте-суретте BC=AD, BE=DF, AE=CF. BC=AD, BE=DF, AE=CF. a)a) ∆∆ ADF=∆CBE ADF=∆CBE екенінекенін ;; b)b) ∆∆ ABE=∆CDF ABE=∆CDF екенінекенін дәлелде.дәлелде. A B D C 5- суретE F

8 слайд

44 . . 44 -суретте-суретте KT=DM, KM=DT. ∆TKM=∆MDT KT=DM, KM=DT. ∆TKM=∆MDT екенін дәлелде.екенін дәлелде. T M K D 4- сурет55 .. 55 -суретте-суретте BC=AD, BE=DF, AE=CF. BC=AD, BE=DF, AE=CF. a)a) ∆∆ ADF=∆CBE ADF=∆CBE екенінекенін ;; b)b) ∆∆ ABE=∆CDF ABE=∆CDF екенінекенін дәлелде.дәлелде. A B D C 5- суретE F

9 слайд
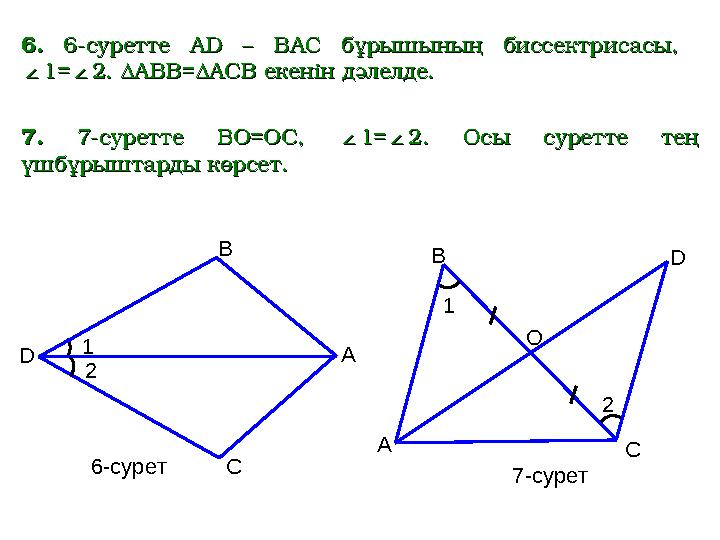
66 .. 66 -суретте-суретте AD – BAC AD – BAC бұрышының биссектрисасы,бұрышының биссектрисасы, ∠1=∠2∠1=∠2 .. ∆AB ∆AB ВВ =∆A=∆A СВСВ екенін дәлелде.екенін дәлелде. AB СD 1 2 6 - сурет77 .. 77 -суретте-суретте BO=OC, ∠1=∠2 BO=OC, ∠1=∠2 .. Осы суретте тең Осы суретте тең үшбұрыштарды көрсет.үшбұрыштарды көрсет. A B D C 7 - суретO1 2

9 слайд

66 .. 66 -суретте-суретте AD – BAC AD – BAC бұрышының биссектрисасы,бұрышының биссектрисасы, ∠1=∠2∠1=∠2 .. ∆AB ∆AB ВВ =∆A=∆A СВСВ екенін дәлелде.екенін дәлелде. AB СD 1 2 6 - сурет77 .. 77 -суретте-суретте BO=OC, ∠1=∠2 BO=OC, ∠1=∠2 .. Осы суретте тең Осы суретте тең үшбұрыштарды көрсет.үшбұрыштарды көрсет. A B D C 7 - суретO1 2

10 слайд
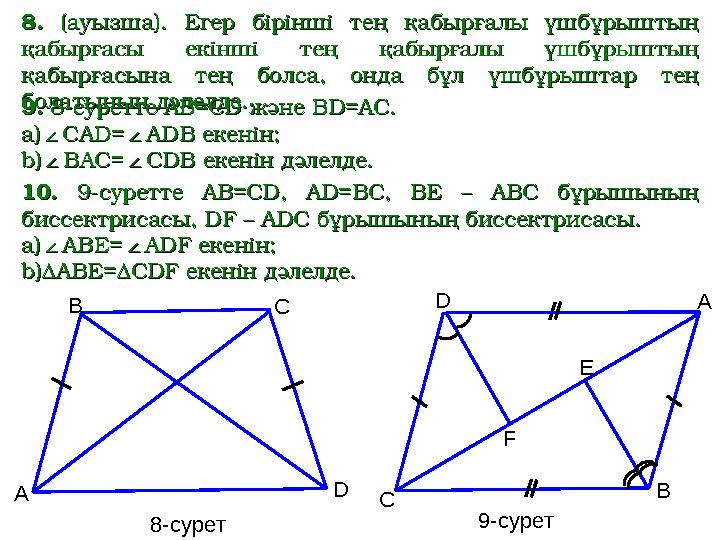
8.8. (ауызша). Егер бірінші тең қабырғалы үшбұрыштың (ауызша). Егер бірінші тең қабырғалы үшбұрыштың қабырғасы екінші тең қабырғалы үшбұрыштың қабырғасы екінші тең қабырғалы үшбұрыштың қабырғасына тең болса, онда бұл үшбұрыштар тең қабырғасына тең болса, онда бұл үшбұрыштар тең болатынын дәлелде.болатынын дәлелде. 9.9. 8-суретте АВ=CD және BD=АС. 8-суретте АВ=CD және BD=АС. a)a) ∠∠ CAD=CAD= ∠∠ ADB екенін;ADB екенін; b)b) ∠∠ BAC=BAC= ∠∠ CDB екенін дәлелде.CDB екенін дәлелде. A B DC 8 - сурет10.10. 9-суретте АВ=CD 9-суретте АВ=CD ,, AA D=D= BB СС , BE, BE – – ABCABC бұрышының бұрышының биссектрисасы, биссектрисасы, DFDF – – ADCADC бұрышының биссектрисасы бұрышының биссектрисасы .. a)a) ∠∠ АВЕ=АВЕ= ∠∠ ADAD FF екенін; екенін; b)b) ∆∆ ABE=∆CDF ABE=∆CDF екенінекенін дәлелдедәлелде .. A BD C 9 - сурет E F

10 слайд

8.8. (ауызша). Егер бірінші тең қабырғалы үшбұрыштың (ауызша). Егер бірінші тең қабырғалы үшбұрыштың қабырғасы екінші тең қабырғалы үшбұрыштың қабырғасы екінші тең қабырғалы үшбұрыштың қабырғасына тең болса, онда бұл үшбұрыштар тең қабырғасына тең болса, онда бұл үшбұрыштар тең болатынын дәлелде.болатынын дәлелде. 9.9. 8-суретте АВ=CD және BD=АС. 8-суретте АВ=CD және BD=АС. a)a) ∠∠ CAD=CAD= ∠∠ ADB екенін;ADB екенін; b)b) ∠∠ BAC=BAC= ∠∠ CDB екенін дәлелде.CDB екенін дәлелде. A B DC 8 - сурет10.10. 9-суретте АВ=CD 9-суретте АВ=CD ,, AA D=D= BB СС , BE, BE – – ABCABC бұрышының бұрышының биссектрисасы, биссектрисасы, DFDF – – ADCADC бұрышының биссектрисасы бұрышының биссектрисасы .. a)a) ∠∠ АВЕ=АВЕ= ∠∠ ADAD FF екенін; екенін; b)b) ∆∆ ABE=∆CDF ABE=∆CDF екенінекенін дәлелдедәлелде .. A BD C 9 - сурет E F

11 слайд
11*.11*. ABC және А ABC және А 11 ВВ 11 СС 11 үшбұрыштарында BМ және В үшбұрыштарында BМ және В 11 ММ 11 медианалар өзара тең, АB=Амедианалар өзара тең, АB=А 11 ВВ 11 , , АС=ААС=А 11 СС 11 . . ∆∆ АВСАВС == ∆∆ АА 11 ВВ 11 СС 11 екенін дәлелде.екенін дәлелде. 12*.12*. ABC және А ABC және А 11 ВВ 11 СС 11 үшбұрыштарында A үшбұрыштарында A D D және және АА 11 DD 11 кесінділері кесінділері – – биссектрисалар, биссектрисалар, АB=ААB=А 11 ВВ 11 , , B B DD =В=В 11 DD 11 және және ADAD == AA 11 DD 11 . . ∆∆ АВСАВС == ∆∆ АА 11 ВВ 11 СС 11 екенін дәлелде.екенін дәлелде. 11 33 *.*. ADC ADC жәнежәне BCD тең бүйірлі үшбұрыштарының DC BCD тең бүйірлі үшбұрыштарының DC табаны ортақ. АВ түзуі CD кесіндісін О нүктесінде қияды.табаны ортақ. АВ түзуі CD кесіндісін О нүктесінде қияды. а) а) ∠∠ ADB=ADB= ∠∠ ACB;ACB; б) DO = ОС.б) DO = ОС.

11 слайд

11*.11*. ABC және А ABC және А 11 ВВ 11 СС 11 үшбұрыштарында BМ және В үшбұрыштарында BМ және В 11 ММ 11 медианалар өзара тең, АB=Амедианалар өзара тең, АB=А 11 ВВ 11 , , АС=ААС=А 11 СС 11 . . ∆∆ АВСАВС == ∆∆ АА 11 ВВ 11 СС 11 екенін дәлелде.екенін дәлелде. 12*.12*. ABC және А ABC және А 11 ВВ 11 СС 11 үшбұрыштарында A үшбұрыштарында A D D және және АА 11 DD 11 кесінділері кесінділері – – биссектрисалар, биссектрисалар, АB=ААB=А 11 ВВ 11 , , B B DD =В=В 11 DD 11 және және ADAD == AA 11 DD 11 . . ∆∆ АВСАВС == ∆∆ АА 11 ВВ 11 СС 11 екенін дәлелде.екенін дәлелде. 11 33 *.*. ADC ADC жәнежәне BCD тең бүйірлі үшбұрыштарының DC BCD тең бүйірлі үшбұрыштарының DC табаны ортақ. АВ түзуі CD кесіндісін О нүктесінде қияды.табаны ортақ. АВ түзуі CD кесіндісін О нүктесінде қияды. а) а) ∠∠ ADB=ADB= ∠∠ ACB;ACB; б) DO = ОС.б) DO = ОС.