7 сынып алгебра
7 сынып алгебра

#1 слайд
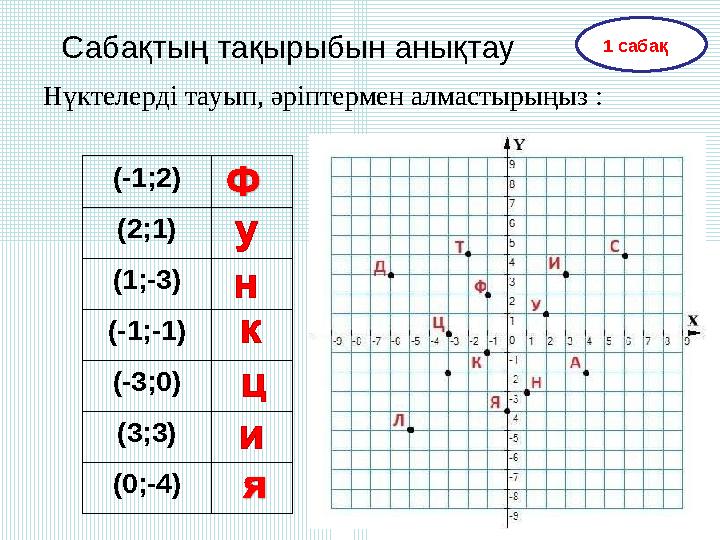
Сабақтың тақырыбын анықтау
Нүктелерді тауып, әріптермен алмастырыңыз :
(-1;2)
(2;1)
(1;-3)
(-1;-1)
(-3;0)
(3;3)
(0;-4)
1 сабақ
1 слайд
Сабақтың тақырыбын анықтау Нүктелерді тауып, әріптермен алмастырыңыз : (-1;2) (2;1) (1;-3) (-1;-1) (-3;0) (3;3) (0;-4) 1 сабақ

#2 слайд
Сабақтың тақырыбы:
«Функция.Функцияның
графигі»
Сабақтың мақсаты:
7.4.1.1 функция және функцияның графигі ұғымдарын
меңгеру;
7.4.1.2 функцияның берілу тәсілдерін білу;
2 слайд
Сабақтың тақырыбы: «Функция.Функцияның графигі» Сабақтың мақсаты: 7.4.1.1 функция және функцияның графигі ұғымдарын меңгеру; 7.4.1.2 функцияның берілу тәсілдерін білу;

#3 слайд
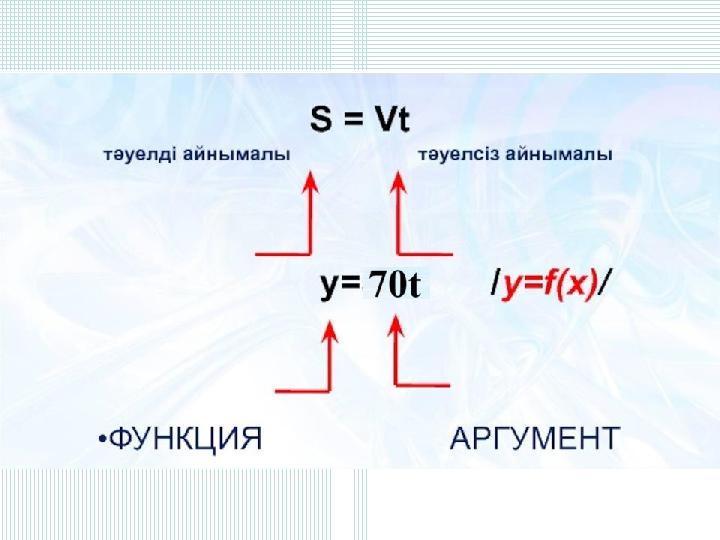
Машина 70 км/сағ жылдамдықпен қозғалып
келеді.Машинаның t сағатта қанша жол
жүретінін табыңыздар. Мұндағы t = 1; 1,5; 3.
Машина t сағатта S = 70 · t км жол жүреді.
Кез-келген уақыттағы жүрілген жолды
оңай анықтауға болады:
Егер t = 1, онда S = 70 · 1 = 70
Егер t = 1,5, онда S = 70 · 1,5 = 105
Егер t = 3, онда S = 70 · 3 = 210
3 слайд
Машина 70 км/сағ жылдамдықпен қозғалып келеді.Машинаның t сағатта қанша жол жүретінін табыңыздар. Мұндағы t = 1; 1,5; 3. Машина t сағатта S = 70 · t км жол жүреді. Кез-келген уақыттағы жүрілген жолды оңай анықтауға болады: Егер t = 1, онда S = 70 · 1 = 70 Егер t = 1,5, онда S = 70 · 1,5 = 105 Егер t = 3, онда S = 70 · 3 = 210

#4 слайд
Тәуелсіз айнымалының әрбір мәніне
тәуелді айнымалының жалғыз ғана мәні
сәйкес келеді. Осындай бір айнымалының
басқа айнымалыдан тәуелділігін
функционалды тәуелділік немесе функция
деп атайды.
4 слайд
Тәуелсіз айнымалының әрбір мәніне тәуелді айнымалының жалғыз ғана мәні сәйкес келеді. Осындай бір айнымалының басқа айнымалыдан тәуелділігін функционалды тәуелділік немесе функция деп атайды.
#5 слайд
5 слайд
#6 слайд
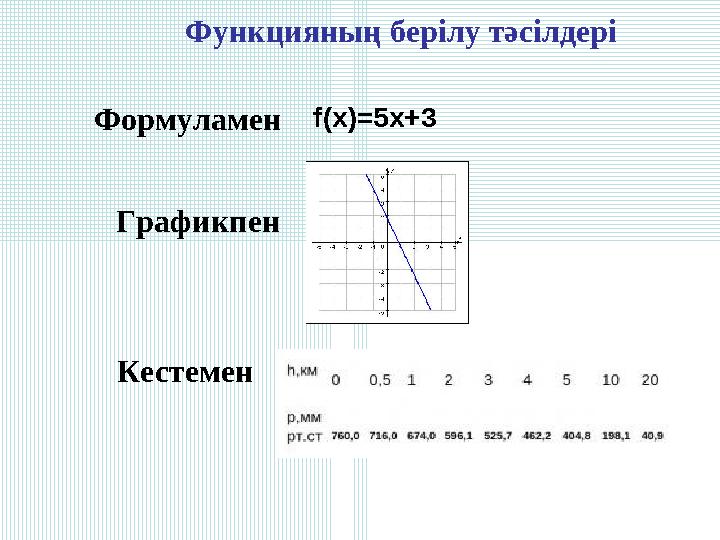
Функцияның берілу тәсілдері
Формуламен f(x)=5x+3
Графикпен
Кестемен
6 слайд
Функцияның берілу тәсілдері Формуламен f(x)=5x+3 Графикпен Кестемен

#7 слайд
7 слайд

#8 слайд
Функцияның формуламен берілуіне есептер
1 мысал. y(x) = x
3
+ x функциясының
х = - 2; х = 5; х = а; х = 3а болғандағы
функцияның мәнін табыңыз
1.у(-2) = (-2)
3
+ (-2) = -8 – 2 = -10
2.у(5) = 5
3
+ 5 = 125 + 5 = 130
3.у(а) = а
3
+ а
4.у(3а) = (3а)
3
+ 3а = 27а
3
+ 3а
8 слайд
Функцияның формуламен берілуіне есептер 1 мысал. y(x) = x 3 + x функциясының х = - 2; х = 5; х = а; х = 3а болғандағы функцияның мәнін табыңыз 1.у(-2) = (-2) 3 + (-2) = -8 – 2 = -10 2.у(5) = 5 3 + 5 = 125 + 5 = 130 3.у(а) = а 3 + а 4.у(3а) = (3а) 3 + 3а = 27а 3 + 3а

#9 слайд
9 слайд
#10 слайд
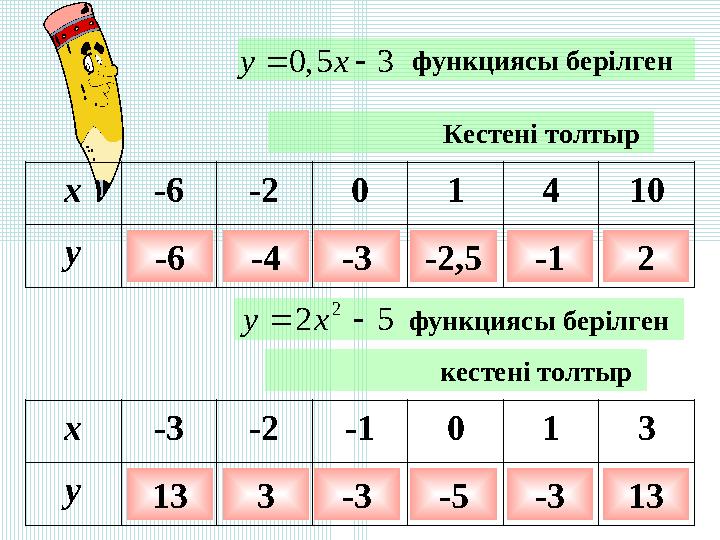
функциясы берілген 0,5 3у х
Кестені толтыр
x-6-20 1 410
y-6-4-3-2,5-12
кестені толтыр
x-3-2-10 1 3
y133-3-5-313
функциясы берілген 52
2
xy
10 слайд
функциясы берілген 0,5 3у х Кестені толтыр x-6-20 1 410 y-6-4-3-2,5-12 кестені толтыр x-3-2-10 1 3 y133-3-5-313 функциясы берілген 52 2 xy
#11 слайд
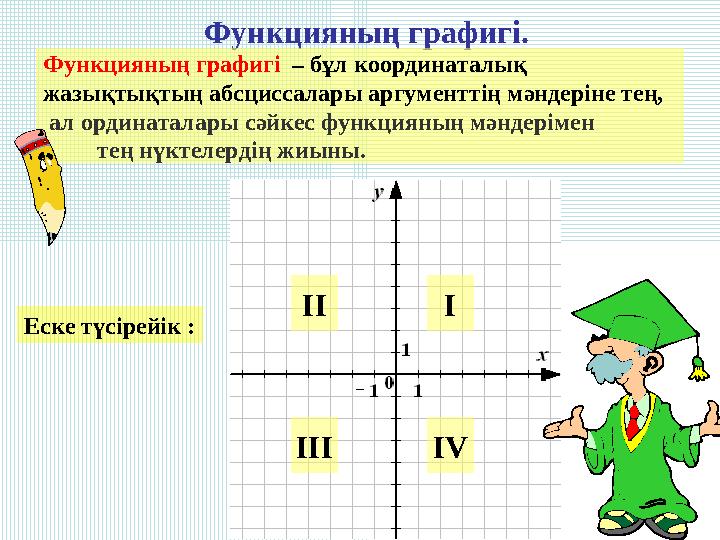
Функцияның графигі.
Функцияның графигі – бұл координаталық
жазықтықтың абсциссалары аргументтің мәндеріне тең,
ал ординаталары сәйкес функцияның мәндерімен
тең нүктелердің жиыны.
Еске түсірейік :
IV III
II I
11 слайд
Функцияның графигі. Функцияның графигі – бұл координаталық жазықтықтың абсциссалары аргументтің мәндеріне тең, ал ординаталары сәйкес функцияның мәндерімен тең нүктелердің жиыны. Еске түсірейік : IV III II I
#12 слайд
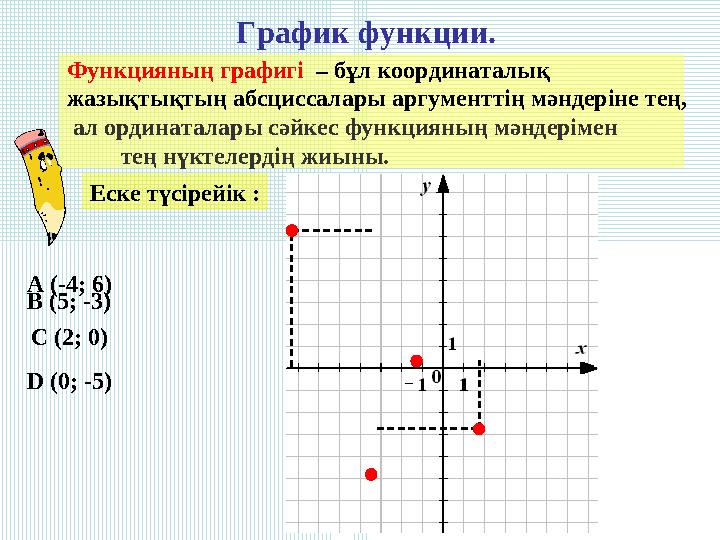
График функции.
Функцияның графигі – бұл координаталық
жазықтықтың абсциссалары аргументтің мәндеріне тең,
ал ординаталары сәйкес функцияның мәндерімен
тең нүктелердің жиыны.
Еске түсірейік :
A (-4; 6)
B (5; -3)
C (2; 0)
D (0; -5)
12 слайд
График функции. Функцияның графигі – бұл координаталық жазықтықтың абсциссалары аргументтің мәндеріне тең, ал ординаталары сәйкес функцияның мәндерімен тең нүктелердің жиыны. Еске түсірейік : A (-4; 6) B (5; -3) C (2; 0) D (0; -5)

#13 слайд
Үйге тапсырма Үйге тапсырма
13 слайд
Үйге тапсырма Үйге тапсырма

#14 слайд
Функция.
Функцияның графигі.
Сабақтың мақсаты:
7.4.1.3 функцияның анықталу
облысы мен мәндер жиынын
табу;
2 сабақ
14 слайд
Функция. Функцияның графигі. Сабақтың мақсаты: 7.4.1.3 функцияның анықталу облысы мен мәндер жиынын табу; 2 сабақ

#15 слайд
15 слайд

#16 слайд
16 слайд

#17 слайд
VtS
fE
fD
Жүрген жолдың формуласын естерімізге
түсірейік:
Тәуелді S айнымалының қабылдайтын
мәндерін
функцияның мәндерінің жиыны деп
атайды.
Тәуелді t айнымалының барлық мәндері
функцияның анықталу облысын
құрайды
.
.
17 слайд
VtS fE fD Жүрген жолдың формуласын естерімізге түсірейік: Тәуелді S айнымалының қабылдайтын мәндерін функцияның мәндерінің жиыны деп атайды. Тәуелді t айнымалының барлық мәндері функцияның анықталу облысын құрайды . .

#18 слайд
18 слайд

#19 слайд
Тәуелді айнымалының мәндерінің
жиыны функцияның мәндерінің
аймағы деп аталады.
Мысал: y=2x функциясының анықтал
у аймағы -1≤ x ≤ 3 болғанда
функцияның мәндерінің аймағын
табайық.
Санды теңсіздіктердің қасиеттері
бойынша:
-1≤ x ≤ 3 ;
- 2 ≤ 2 x ≤ 6;
Мәндерінің аймағы [ -2;6 ] аралығы
болады.
19 слайд
Тәуелді айнымалының мәндерінің жиыны функцияның мәндерінің аймағы деп аталады. Мысал: y=2x функциясының анықтал у аймағы -1≤ x ≤ 3 болғанда функцияның мәндерінің аймағын табайық. Санды теңсіздіктердің қасиеттері бойынша: -1≤ x ≤ 3 ; - 2 ≤ 2 x ≤ 6; Мәндерінің аймағы [ -2;6 ] аралығы болады.

#20 слайд
1. f ( x)=2x-5 функцисының
мәндерін
х= -2; -1;0; 1;2 болғанда
анықтаңдар
f ( -2)=
f ( -1)=
f ( 0)=
f ( 1)=
f ( 2)=
20 слайд
1. f ( x)=2x-5 функцисының мәндерін х= -2; -1;0; 1;2 болғанда анықтаңдар f ( -2)= f ( -1)= f ( 0)= f ( 1)= f ( 2)=

#21 слайд
2.
f ( x)=2x-5 функцисының мәні
аргументтің қандай мәнінде 3 ; -1; 0;
10 -ға тең?
2х-5=3 2x-5=-1 2x-5=0
2x-5=10
2 x=8 2x=4 2x=5
2x=15
X=4 X=2 X=2,5
X=7,5
21 слайд
2. f ( x)=2x-5 функцисының мәні аргументтің қандай мәнінде 3 ; -1; 0; 10 -ға тең? 2х-5=3 2x-5=-1 2x-5=0 2x-5=10 2 x=8 2x=4 2x=5 2x=15 X=4 X=2 X=2,5 X=7,5

#22 слайд
3 .
22 слайд
3 .

#23 слайд
Тапсырма .
Функцияның анықталу облысын табыңыз :
1.
52
42
xx
x
y
3
2
2
53
x
x
x
x
y2.
3.
7
1
5
14
x
x
y
5 ,2 xx
3 ,2 xx
7x
23 слайд
Тапсырма . Функцияның анықталу облысын табыңыз : 1. 52 42 xx x y 3 2 2 53 x x x x y2. 3. 7 1 5 14 x x y 5 ,2 xx 3 ,2 xx 7x

#24 слайд
24 слайд

#25 слайд
Үйге тапсырма Үйге тапсырма
25 слайд
Үйге тапсырма Үйге тапсырма

#26 слайд
Сабақтың тақырыбы:
«Сызықтық функция және оның
графигі»
3 сабақ
26 слайд
Сабақтың тақырыбы: «Сызықтық функция және оның графигі» 3 сабақ
#27 слайд
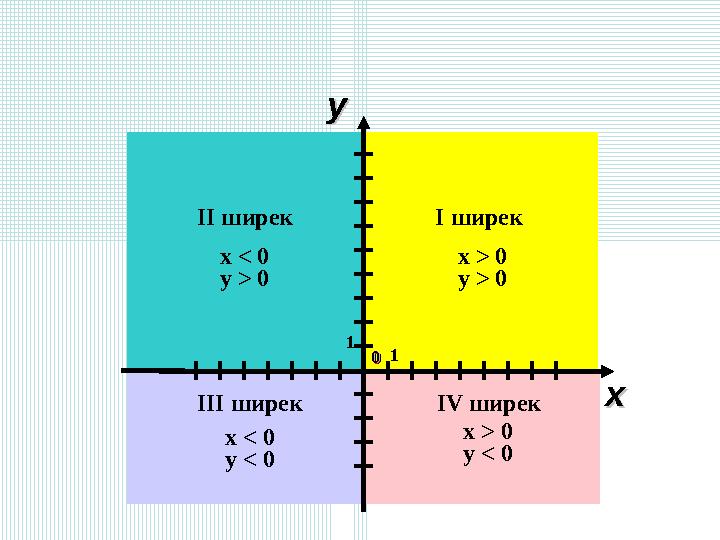
I ширек
x > 0
y > 0
IV ширек
x > 0
y < 0
III ширек
x < 0
y < 0
II ширек
x < 0
y > 0
1
10000
xx
yy
27 слайд
I ширек x > 0 y > 0 IV ширек x > 0 y < 0 III ширек x < 0 y < 0 II ширек x < 0 y > 0 1 10000 xx yy

#28 слайд
у = у = kxkx
28 слайд
у = у = kxkx
#29 слайд
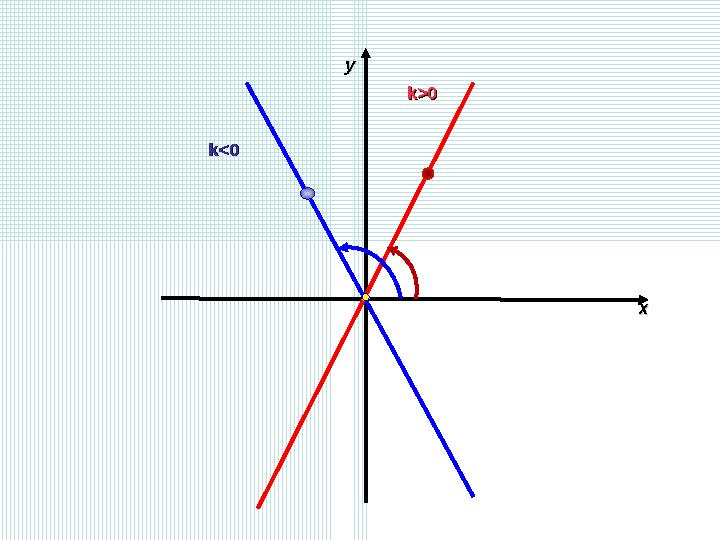
k>0k>0
уу
хх
k<0k<0
29 слайд
k>0k>0 уу хх k<0k<0

#30 слайд
у = kx функциясының графигі С (4;-8)
нүктесі арқылы өтеді, k мәнін тап .
4k=-8
k=-2
30 слайд
у = kx функциясының графигі С (4;-8) нүктесі арқылы өтеді, k мәнін тап . 4k=-8 k=-2
#31 слайд
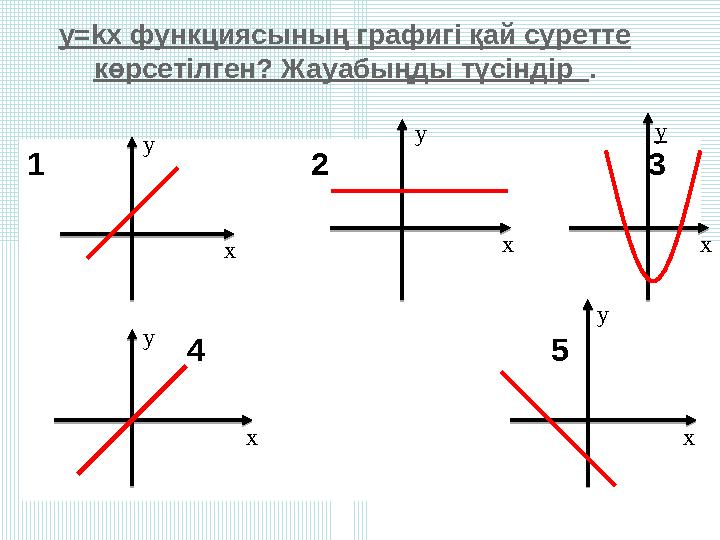
y=kx функциясының графигі қай суретте
көрсетілген? Жауабыңды түсіндір .
1 2 3
4 5
x
y
x
y
x
y
x
y
x
y
31 слайд
y=kx функциясының графигі қай суретте көрсетілген? Жауабыңды түсіндір . 1 2 3 4 5 x y x y x y x y x y

#32 слайд
Функцияның графигін
салыңыз
•1 нұсқа
у=-х
у= 5х
•2 нұсқа
у=-4х
у=2х
32 слайд
Функцияның графигін салыңыз •1 нұсқа у=-х у= 5х •2 нұсқа у=-4х у=2х
#33 слайд
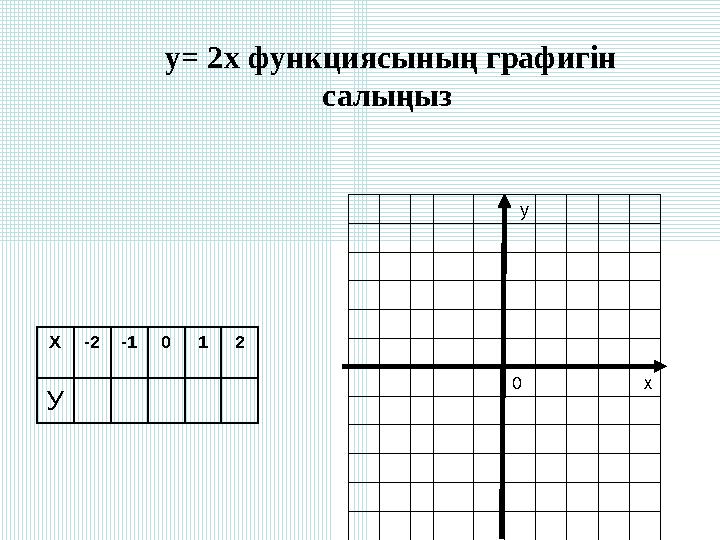
Х-2-1012
У
у
0 х
y= 2x функциясының графигін
салыңыз
33 слайд
Х-2-1012 У у 0 х y= 2x функциясының графигін салыңыз
#34 слайд
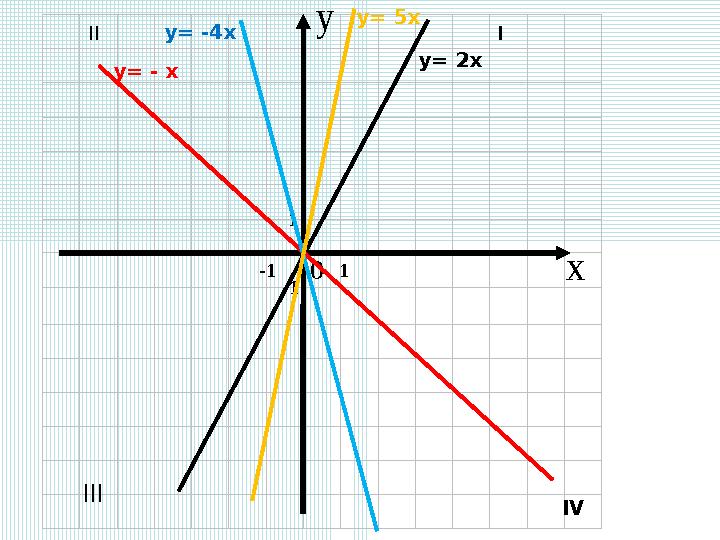
II I
x
y
01
1
-1
-1
y= 5x
III
IV
y= 2x
y= - x
y= -4x
34 слайд
II I x y 01 1 -1 -1 y= 5x III IV y= 2x y= - x y= -4x

#35 слайд
Үйге тапсырма Үйге тапсырма
35 слайд
Үйге тапсырма Үйге тапсырма

#36 слайд
Сызықтық функция және оның
графигі
4 сабақ
36 слайд
Сызықтық функция және оның графигі 4 сабақ

#37 слайд
n=5d+65
кәмпиттер санына байланысты
1-тапсырма .
Анам құны 5тг тұратын бірнеше кәмпит және 65 тг
бір шоколад сатып алды. Ол барлығына қанша
төледі? Сатып алу құнын есептеуге болатын өрнек
жасаңыз.
n- барлық заттың құны
d-кәмпиттер саны
Сатып алу құны неге байланысты деп ойлайсыз?
37 слайд
n=5d+65 кәмпиттер санына байланысты 1-тапсырма . Анам құны 5тг тұратын бірнеше кәмпит және 65 тг бір шоколад сатып алды. Ол барлығына қанша төледі? Сатып алу құнын есептеуге болатын өрнек жасаңыз. n- барлық заттың құны d-кәмпиттер саны Сатып алу құны неге байланысты деп ойлайсыз?

#38 слайд
122ху
213ху
78,2ху
38 слайд
122ху 213ху 78,2ху
#39 слайд
39 слайд

#40 слайд
Дербес жағдайларды қарастырайық.
1) Егер b = 0болса, онда y = kx +
b формуласы
y = kx (k <0, k> 0) түрінде болады.
Бұл формула тура
пропорционалдылық - сызықтық
функцияның дербес жағдайы болып
табылады.
40 слайд
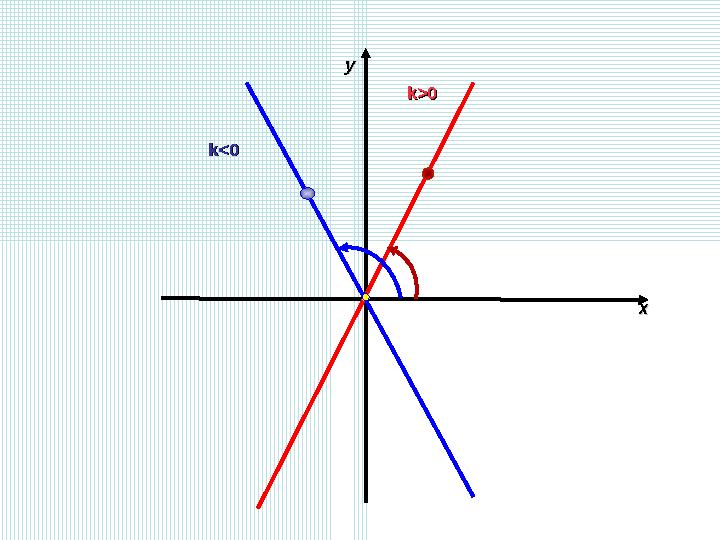
Дербес жағдайларды қарастырайық. 1) Егер b = 0болса, онда y = kx + b формуласы y = kx (k <0, k> 0) түрінде болады. Бұл формула тура пропорционалдылық - сызықтық функцияның дербес жағдайы болып табылады.
#41 слайд
k>0k>0
уу
хх
k<0k<0
41 слайд
k>0k>0 уу хх k<0k<0

#42 слайд
2) Егер k = 0 болса, онда y = kx + b
формуласы y = b түрінде
болады
(графигі х осіне параллель)
42 слайд
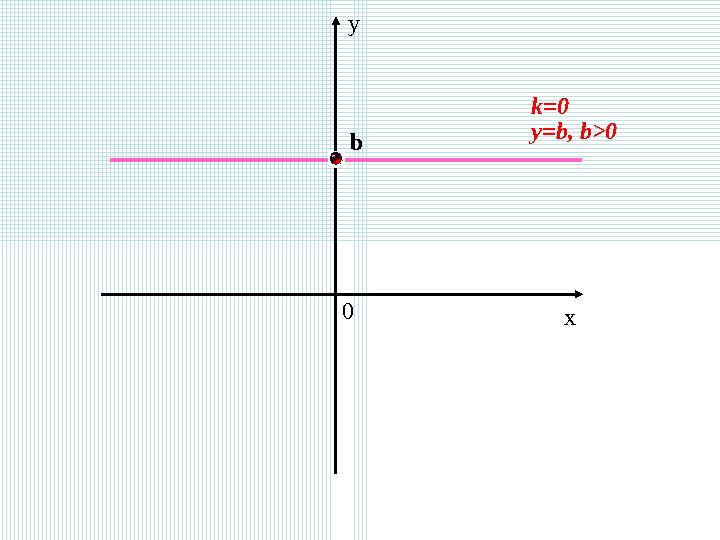
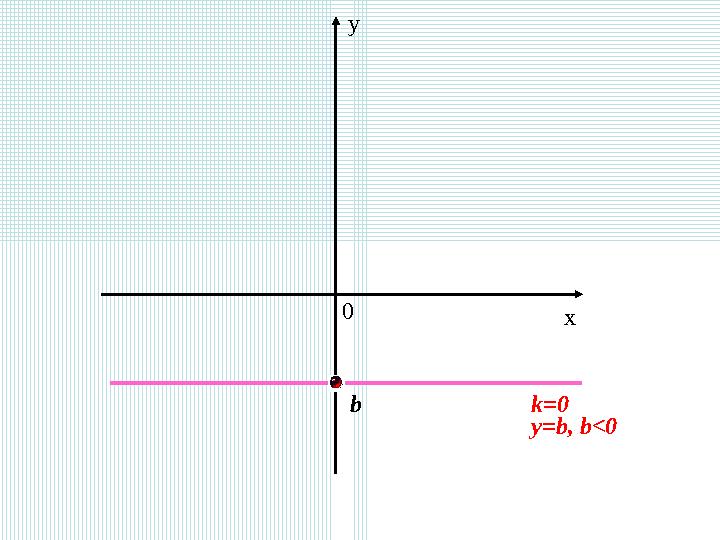
2) Егер k = 0 болса, онда y = kx + b формуласы y = b түрінде болады (графигі х осіне параллель)
#43 слайд
x
y
0
y=b, b>0
b
k=0
43 слайд
x y 0 y=b, b>0 b k=0
#44 слайд
x
y
0
y=b, b<0
b k=0
44 слайд
x y 0 y=b, b<0 b k=0

#45 слайд
у = 3х-2 функциясыны ң
графигі А (5;13) нүктесі
арқылы өтеді ме?
3*5 – 2 =13
45 слайд
у = 3х-2 функциясыны ң графигі А (5;13) нүктесі арқылы өтеді ме? 3*5 – 2 =13

#46 слайд
Төмендегі функциялардың қайсысы
сызықтық болып табылады?
х
у
4
45
3
хху 1ху
4у
ху4,0
0у
4
2
ху
25ху
46 слайд
Төмендегі функциялардың қайсысы сызықтық болып табылады? х у 4 45 3 хху 1ху 4у ху4,0 0у 4 2 ху 25ху
#47 слайд
Сызықтық функция және оның графигі
у = kx+ b ( мұндағы х – тәуелсіз айнымалы , k және b
нақты сандар ) түріндегі формуламен берілген
функцияны сызықтық функция деп атайды.
Сызықтық функция графигін салуды үйренейік
47 слайд
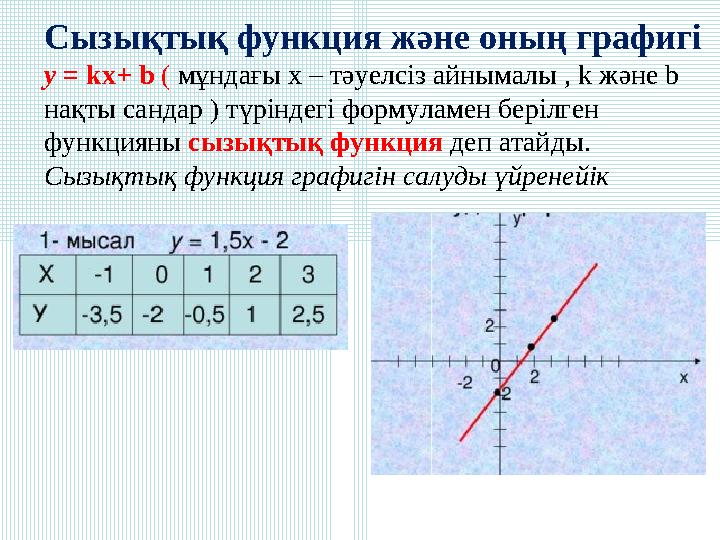
Сызықтық функция және оның графигі у = kx+ b ( мұндағы х – тәуелсіз айнымалы , k және b нақты сандар ) түріндегі формуламен берілген функцияны сызықтық функция деп атайды. Сызықтық функция графигін салуды үйренейік
#48 слайд
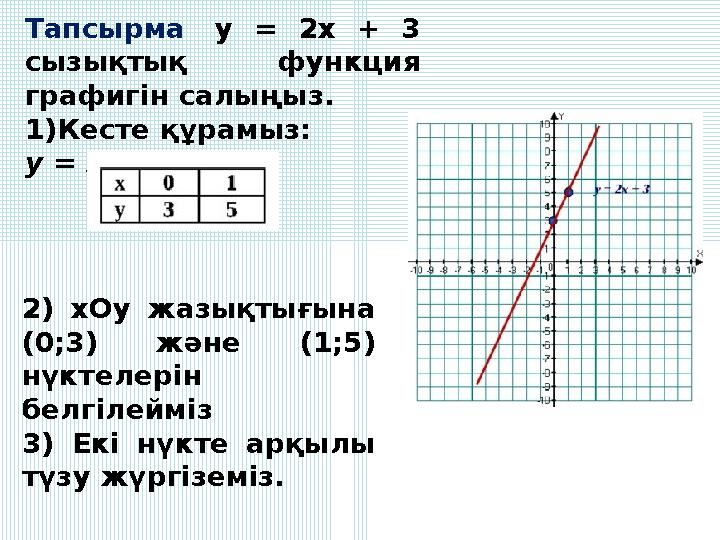
Тапсырма y = 2x + 3
сызықтық функция
графигін салыңыз.
1)Кесте құрамыз:
y = 2x + 3
2) xОy жазықтығына
(0;3) және (1;5)
нүктелерін
белгілейміз
3) Екі нүкте арқылы
түзу жүргіземіз.
48 слайд
Тапсырма y = 2x + 3 сызықтық функция графигін салыңыз. 1)Кесте құрамыз: y = 2x + 3 2) xОy жазықтығына (0;3) және (1;5) нүктелерін белгілейміз 3) Екі нүкте арқылы түзу жүргіземіз.

#49 слайд
49 слайд

#50 слайд
Берілген функциялардың графиктерін
салыңдар
a.y=3x
ә) y=-5x+7
б) y=2
b) y=-3
50 слайд
Берілген функциялардың графиктерін салыңдар a.y=3x ә) y=-5x+7 б) y=2 b) y=-3

#51 слайд
Үйге тапсырма Үйге тапсырма
51 слайд
Үйге тапсырма Үйге тапсырма

#52 слайд
Сызықтық функция және оның
графигі
5 сабақ
52 слайд
Сызықтық функция және оның графигі 5 сабақ

#53 слайд
Функциялардың қайсысы сызықтық екенін анықтаңыз
(
яғни
y=kx+b )
түрі және олардың әрқайсысы үшін
k
және
b .
коэффициенттерінің мәнін жазыңыз
1. y = 0,1x
3. y = -x + 4
4. y = 3x + x
2
5. y = 5x - 3
7. y = 100 + 0,5x
8. y = 1 – x
10. y = 2
k = 0,1; b = 0
k = -1; b = 4
k = 5; b = -3
k = 0,5; b = 100
k = -1; b = 1
k = 0; b = 2
Сызықтықфункцияда
b =0 ,
болса онда
y=kx
турапропорционал
,
мұндағы
k ≠0,.
53 слайд
Функциялардың қайсысы сызықтық екенін анықтаңыз ( яғни y=kx+b ) түрі және олардың әрқайсысы үшін k және b . коэффициенттерінің мәнін жазыңыз 1. y = 0,1x 3. y = -x + 4 4. y = 3x + x 2 5. y = 5x - 3 7. y = 100 + 0,5x 8. y = 1 – x 10. y = 2 k = 0,1; b = 0 k = -1; b = 4 k = 5; b = -3 k = 0,5; b = 100 k = -1; b = 1 k = 0; b = 2 Сызықтықфункцияда b =0 , болса онда y=kx турапропорционал , мұндағы k ≠0,.
#54 слайд
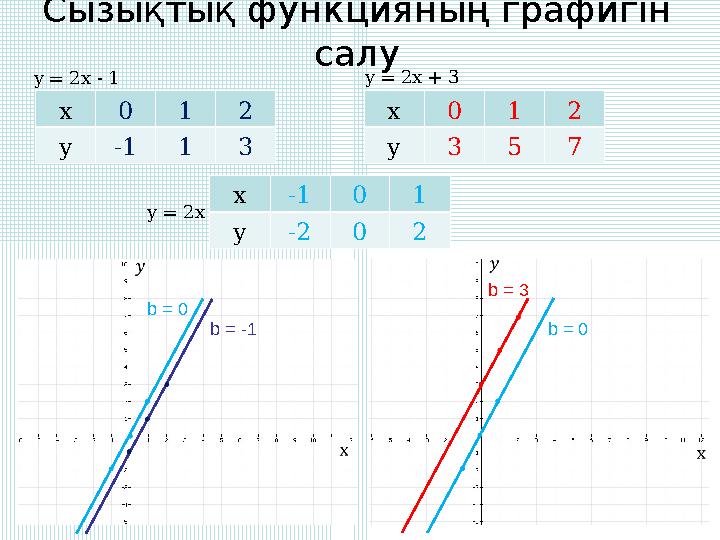
Сызықтықфункцияныңграфигін
салу
y = 2x - 1 y = 2x + 3
b = -1
b = 3
x012
y-113
x012
y357
y = 2x
x-101
y-202
b = 0
b = 0
54 слайд
Сызықтықфункцияныңграфигін салу y = 2x - 1 y = 2x + 3 b = -1 b = 3 x012 y-113 x012 y357 y = 2x x-101 y-202 b = 0 b = 0

#55 слайд
Қандайфункциялардыңграфиктері
?
координатаныңбаснүктесіарқылыөтеді
1. y = 7x
2. y = -
5x+1
3. s = -3t
4. u = 4v-2
5. g = 2f
6. y = -4x
7. y = 100 + 0,5x
8. a = 1 –3b
9. f = 5 +3h
10. y = 0,2x
55 слайд
Қандайфункциялардыңграфиктері ? координатаныңбаснүктесіарқылыөтеді 1. y = 7x 2. y = - 5x+1 3. s = -3t 4. u = 4v-2 5. g = 2f 6. y = -4x 7. y = 100 + 0,5x 8. a = 1 –3b 9. f = 5 +3h 10. y = 0,2x

#56 слайд
Функция графиктері қандай квадранттарда
орналасқанын анықтаңыз
1. =
у
2
х
2. = -
у
5
х
I және III ширек II және IV ширек
3. = -
у
6
х
4. =
у х
5. = 8
у х
6. = -1,5
у х
7. = -(-3 )
у х
8. - = 4
у х
56 слайд
Функция графиктері қандай квадранттарда орналасқанын анықтаңыз 1. = у 2 х 2. = - у 5 х I және III ширек II және IV ширек 3. = - у 6 х 4. = у х 5. = 8 у х 6. = -1,5 у х 7. = -(-3 ) у х 8. - = 4 у х
#57 слайд
y
x
y = x; k>0
y= -x ; k<0
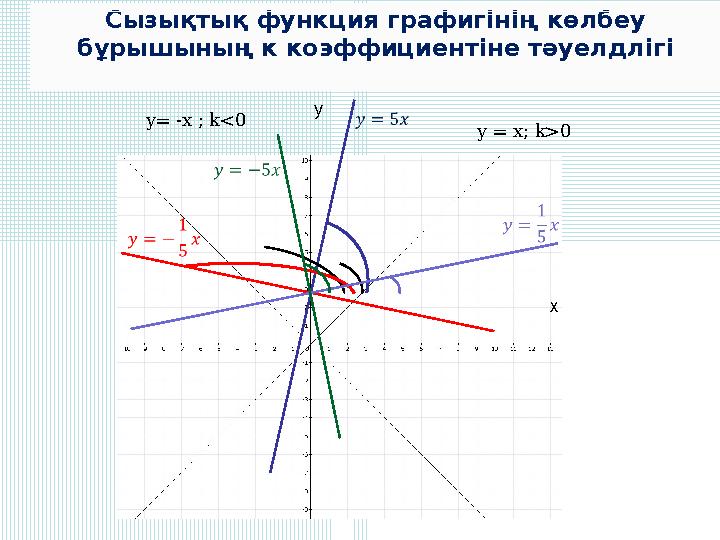
Сызықтық функция графигінің көлбеу
бұрышының к коэффициентіне тәуелдлігі
57 слайд
y x y = x; k>0 y= -x ; k<0 Сызықтық функция графигінің көлбеу бұрышының к коэффициентіне тәуелдлігі
#58 слайд
y = 2x
y= -3x
y
x
K
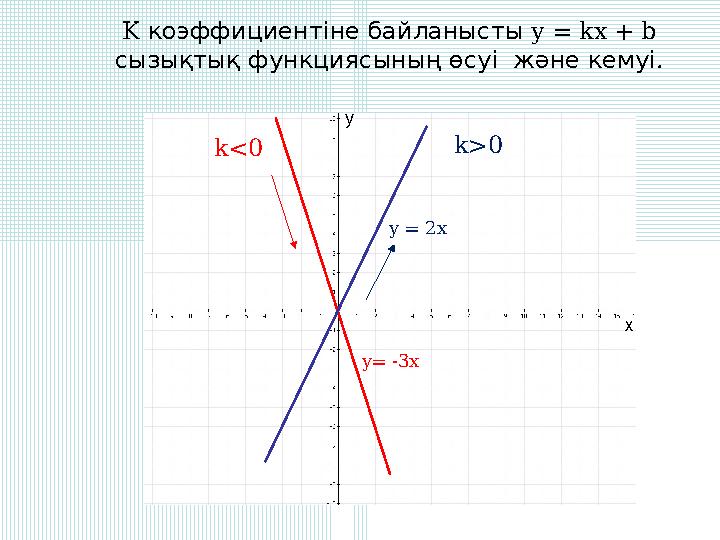
коэффициентіне байланысты
y = kx + b
.
сызықтық функциясының өсуі және кемуі
k>0k<0
58 слайд
y = 2x y= -3x y x K коэффициентіне байланысты y = kx + b . сызықтық функциясының өсуі және кемуі k>0k<0
#59 слайд
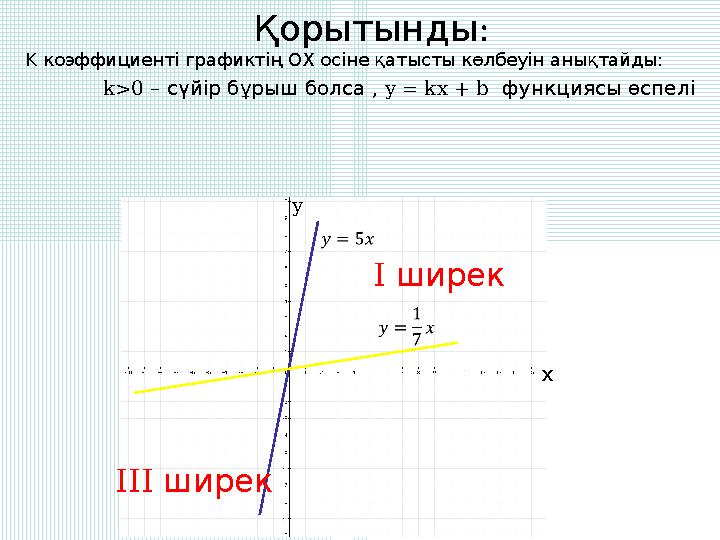
Қорытынды:
K коэффициенті графиктің OX осіне қатысты көлбеуін анықтайды:
k>0 – ,
сүйір бұрыш болса
y = kx + b
функциясы өспелі
y
х
I
ширек
III
ширек
59 слайд
Қорытынды: K коэффициенті графиктің OX осіне қатысты көлбеуін анықтайды: k>0 – , сүйір бұрыш болса y = kx + b функциясы өспелі y х I ширек III ширек
#60 слайд
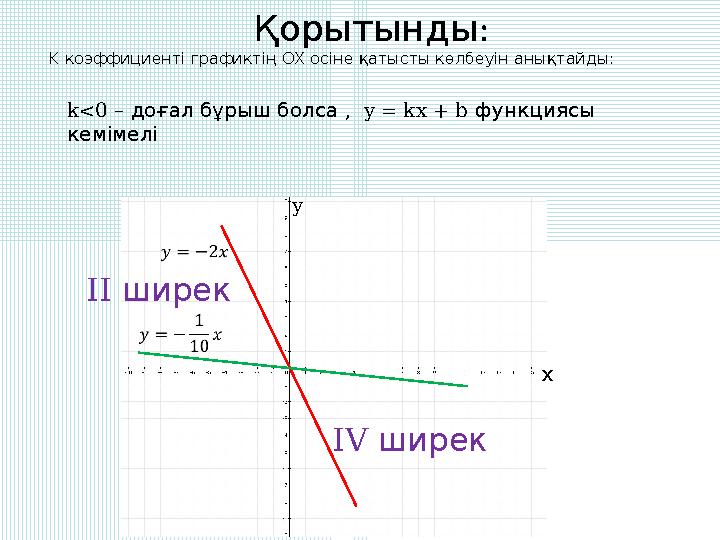
Қорытынды:
K коэффициенті графиктің OX осіне қатысты көлбеуін анықтайды:
k<0 – ,
доғал бұрыш болса
y = kx + b
функциясы
кемімелі
y
х
II
ширек
IV ширек
60 слайд
Қорытынды: K коэффициенті графиктің OX осіне қатысты көлбеуін анықтайды: k<0 – , доғал бұрыш болса y = kx + b функциясы кемімелі y х II ширек IV ширек
#61 слайд
61 слайд
#62 слайд
62 слайд

#63 слайд
Үйге тапсырма Үйге тапсырма
63 слайд
Үйге тапсырма Үйге тапсырма

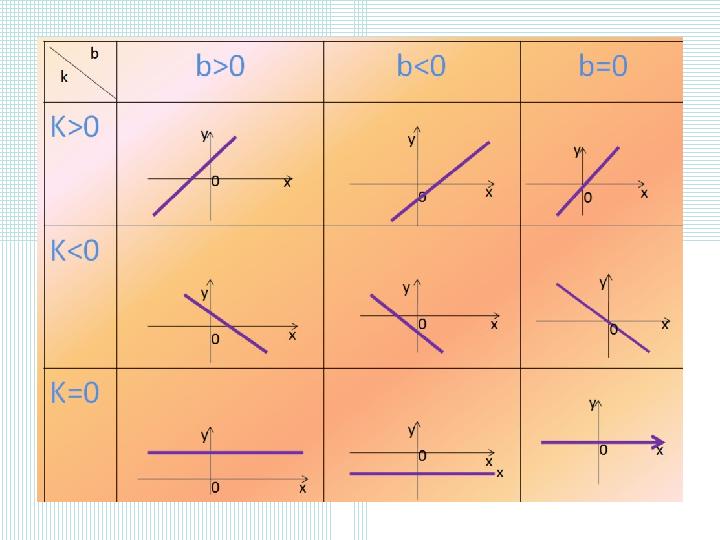
#64 слайд
Сызықтық функция және оның
графигі
Сабақтың мақсаты:
7.4.1.7у = kx + b сызықтық
функциясының графигінен k және b
таңбаларын анықтау;
6 сабақ
64 слайд
Сызықтық функция және оның графигі Сабақтың мақсаты: 7.4.1.7у = kx + b сызықтық функциясының графигінен k және b таңбаларын анықтау; 6 сабақ
#65 слайд
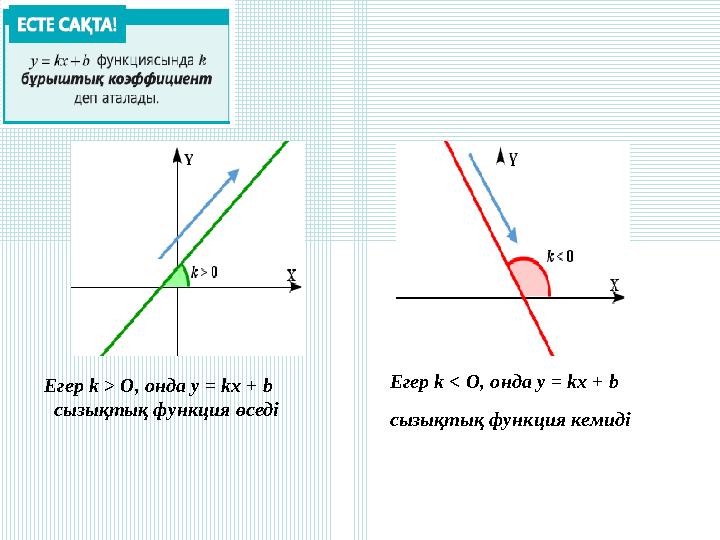
Егер k > О, онда у = kx + b
сызықтық функция өседі
Егер k < О, онда у = kx + b
сызықтық функция кемиді
65 слайд
Егер k > О, онда у = kx + b сызықтық функция өседі Егер k < О, онда у = kx + b сызықтық функция кемиді
#66 слайд
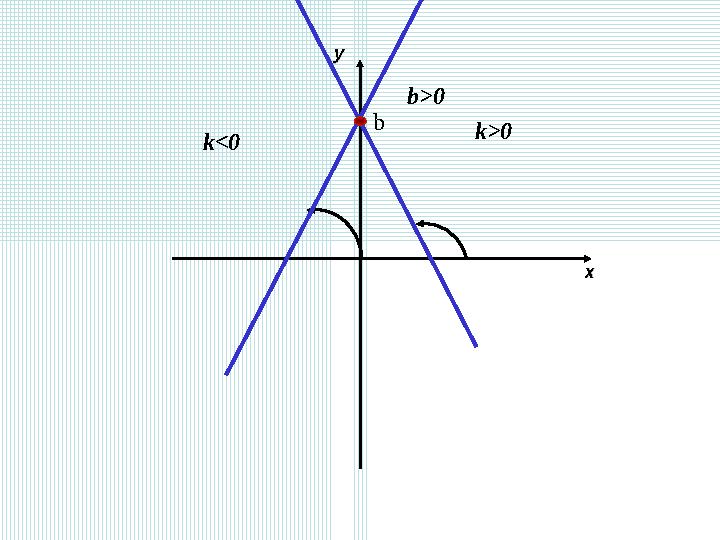
b
k>0
уу
хх
k<0
b>0
66 слайд
b k>0 уу хх k<0 b>0
#67 слайд
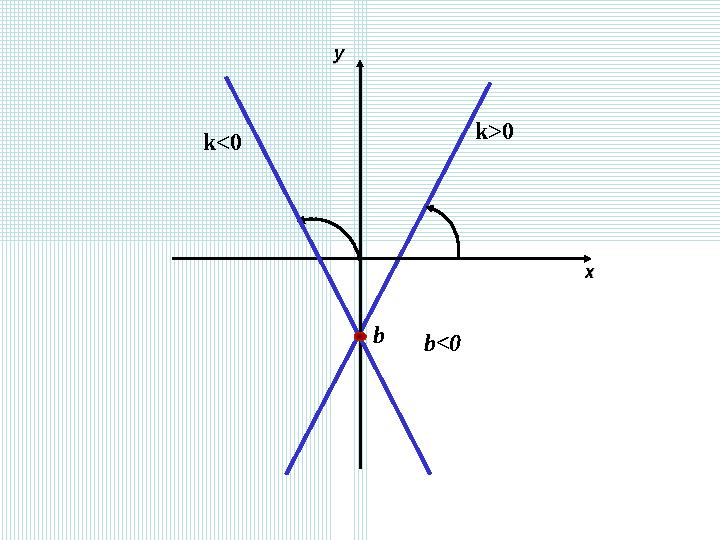
b
k>0
уу
хх
k<0
b<0
67 слайд
b k>0 уу хх k<0 b<0
#68 слайд
68 слайд
#69 слайд
69 слайд
#70 слайд
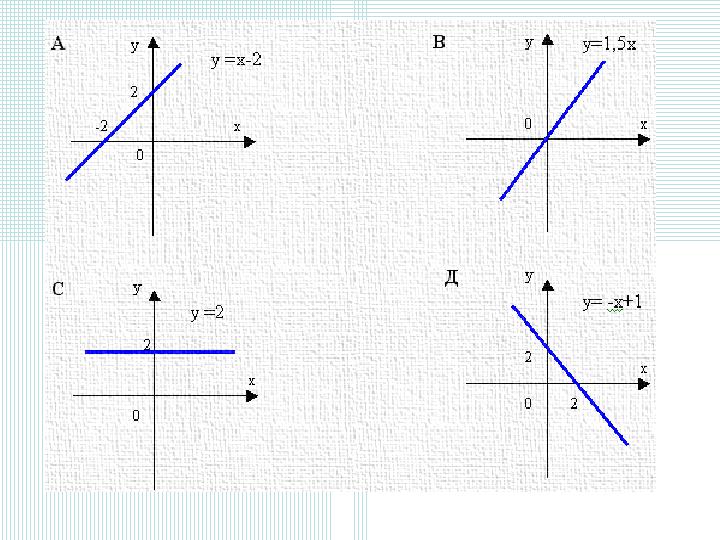
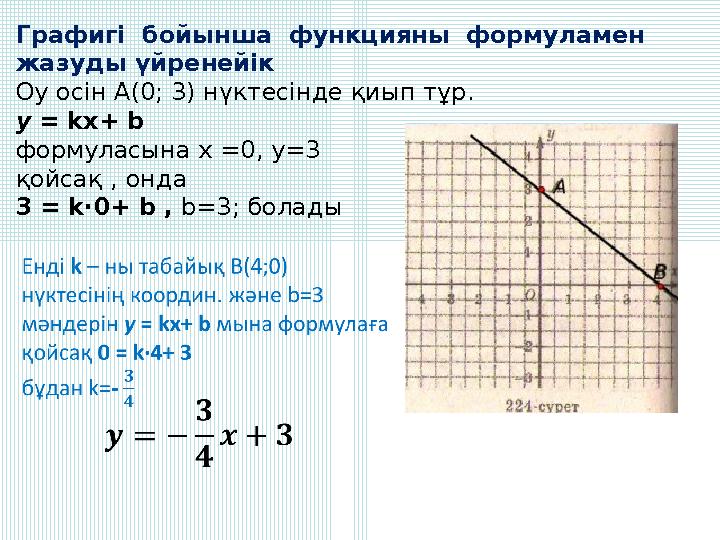
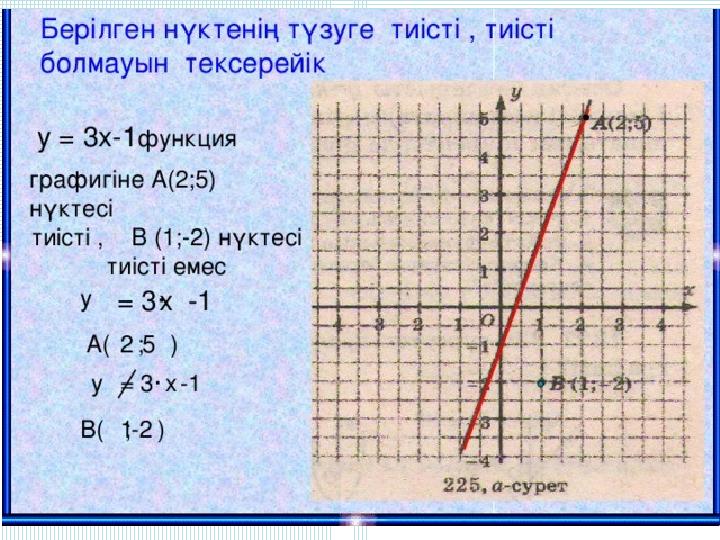
Графигі бойынша функцияны формуламен
жазуды үйренейік
Оу осін А(0; 3) нүктесінде қиып тұр.
у = kx+ b
формуласына х =0, у=3
қойсақ , онда
3 = k∙0+ b , b=3; болады
70 слайд
Графигі бойынша функцияны формуламен жазуды үйренейік Оу осін А(0; 3) нүктесінде қиып тұр. у = kx+ b формуласына х =0, у=3 қойсақ , онда 3 = k∙0+ b , b=3; болады
#71 слайд
71 слайд
#72 слайд
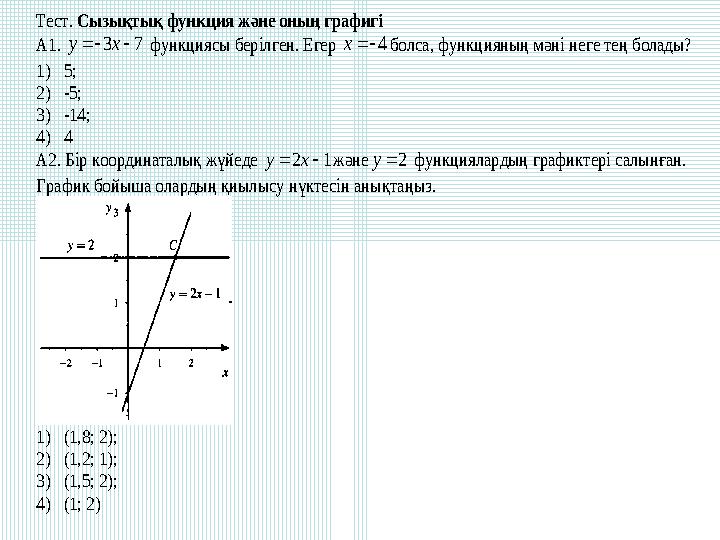
Тест. Сызықтық функция және оның графигі
А1. 73xy функциясы берілген. Егер 4x болса, функцияның мәні неге тең болады?
1) 5;
2) -5;
3) -14;
4) 4
А2. Бір координаталық жүйеде 12xy және2y функциялардың графиктері салынған.
График бойыша олардың қиылысу нүктесін анықтаңыз.
1) (1,8; 2);
2) (1,2; 1);
3) (1,5; 2);
4) (1; 2)
72 слайд
Тест. Сызықтық функция және оның графигі А1. 73xy функциясы берілген. Егер 4x болса, функцияның мәні неге тең болады? 1) 5; 2) -5; 3) -14; 4) 4 А2. Бір координаталық жүйеде 12xy және2y функциялардың графиктері салынған. График бойыша олардың қиылысу нүктесін анықтаңыз. 1) (1,8; 2); 2) (1,2; 1); 3) (1,5; 2); 4) (1; 2)

#73 слайд
А3. 8
2
1
xy функцияның графигі мен абсцисса осінің қиылысу нүктесін табыңыз.
1) (4; 0);
2) (0; 4);
3) (8; 0);
4) (16; 0)
А4. bkxy функцияның графигі берілген. Осы функцияның формуласын жазыңыз.
1) 35,1xy ;
2) 15,1xy ;
3) 32xy ;
4) 32xy
В1. Функциялардың қиылысу нүктесінің координаталырын анықтаңыз xy
3
1
және 52xy
В2. Функцияның мәні 2y болғанда, 68,0 xy функциясы үшін х-тың мәнің табыңыз .
C1. Егер 4kxy функцияның графигі В (-3; 6) нүктесі арқылы өтетін болса, онда осы
функцияның k бұрыштық коэффициентін табыңыз .
73 слайд
А3. 8 2 1 xy функцияның графигі мен абсцисса осінің қиылысу нүктесін табыңыз. 1) (4; 0); 2) (0; 4); 3) (8; 0); 4) (16; 0) А4. bkxy функцияның графигі берілген. Осы функцияның формуласын жазыңыз. 1) 35,1xy ; 2) 15,1xy ; 3) 32xy ; 4) 32xy В1. Функциялардың қиылысу нүктесінің координаталырын анықтаңыз xy 3 1 және 52xy В2. Функцияның мәні 2y болғанда, 68,0 xy функциясы үшін х-тың мәнің табыңыз . C1. Егер 4kxy функцияның графигі В (-3; 6) нүктесі арқылы өтетін болса, онда осы функцияның k бұрыштық коэффициентін табыңыз .

#74 слайд
Үйге тапсырма Үйге тапсырма
74 слайд
Үйге тапсырма Үйге тапсырма

#75 слайд
Сабақтың тақырыбы:Сабақтың тақырыбы:
Сызықтық функциялардың Сызықтық функциялардың
графиктерінің өзара орналасуыграфиктерінің өзара орналасуы
Сабақтың мақсаты:
7.4.1.8 сызықтық функция графиктерінің өзара
орналасуы олардың коэффициенттеріне тәуелді
болатынын негіздеу
7 сабақ
75 слайд
Сабақтың тақырыбы:Сабақтың тақырыбы: Сызықтық функциялардың Сызықтық функциялардың графиктерінің өзара орналасуыграфиктерінің өзара орналасуы Сабақтың мақсаты: 7.4.1.8 сызықтық функция графиктерінің өзара орналасуы олардың коэффициенттеріне тәуелді болатынын негіздеу 7 сабақ

#76 слайд
y=kx+l сызықтық функциядағы l=0 болғандағы
функцияның формуламен у=kx түрінде жазамыз. у=kx
формуласымен берілген функцияны тура
пропорционалдық деп атаймыз.
у= kx тура пропорционалдығы – сызықтық
функция. Сондықтан оның графигі түзу сызық болады.
Мұндағы k-түзудің бұрыштық коэффиценті деп атаймыз.
у= kx тура пропорционалдығындағы х=0 болғанда у=0
болады.
Түзу тік бұрышты координаталар жүйесіндегі
координаталар басы болатын О (0;0) нүктесі арқылы
өтеді.
Егер у= kx+l сызықтық функциядағы k=0 болса,
функция y=l түрінде жазамыз. y=l функциясын тұрақты
функция деп атаймыз. Себебі х-тің кез келген мәнінде у-тің
мәні өзгермейді.
76 слайд
y=kx+l сызықтық функциядағы l=0 болғандағы функцияның формуламен у=kx түрінде жазамыз. у=kx формуласымен берілген функцияны тура пропорционалдық деп атаймыз. у= kx тура пропорционалдығы – сызықтық функция. Сондықтан оның графигі түзу сызық болады. Мұндағы k-түзудің бұрыштық коэффиценті деп атаймыз. у= kx тура пропорционалдығындағы х=0 болғанда у=0 болады. Түзу тік бұрышты координаталар жүйесіндегі координаталар басы болатын О (0;0) нүктесі арқылы өтеді. Егер у= kx+l сызықтық функциядағы k=0 болса, функция y=l түрінде жазамыз. y=l функциясын тұрақты функция деп атаймыз. Себебі х-тің кез келген мәнінде у-тің мәні өзгермейді.

#77 слайд
Сызықтық функцияның графигі –
түзу, демек, сызықтық
функциялардың графиктері бір
нүктеде қиылысады немесе параллель
болады, немесе беттеседі.
77 слайд
Сызықтық функцияның графигі – түзу, демек, сызықтық функциялардың графиктері бір нүктеде қиылысады немесе параллель болады, немесе беттеседі.
#78 слайд
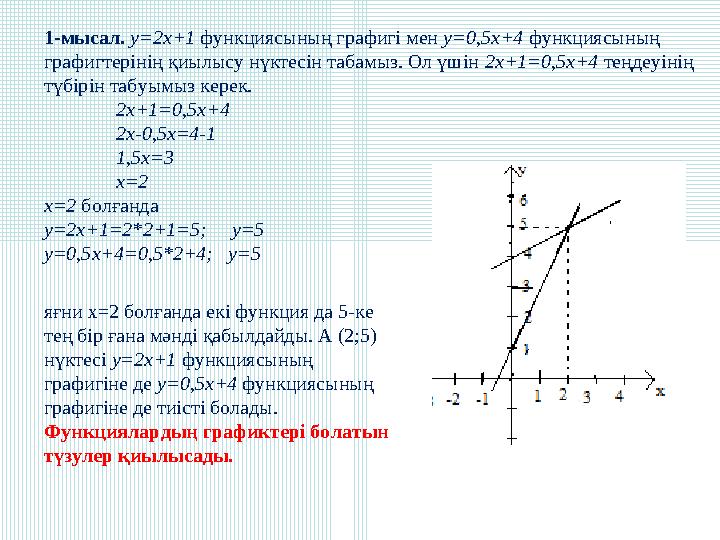
1-мысал. у=2x+1 функциясының графигі мен у=0,5x+4 функциясының
графигтерінің қиылысу нүктесін табамыз. Ол үшін 2х+1=0,5х+4 теңдеуінің
түбірін табуымыз керек.
2х+1=0,5х+4
2х-0,5х=4-1
1,5х=3
х=2
х=2 болғанда
у=2х+1=2*2+1=5; у=5
у=0,5х+4=0,5*2+4; у=5
яғни х=2 болғанда екі функция да 5-ке
тең бір ғана мәнді қабылдайды. А (2;5)
нүктесі у=2х+1 функциясының
графигіне де у=0,5х+4 функциясының
графигіне де тиісті болады.
Функциялардың графиктері болатын
түзулер қиылысады.
78 слайд
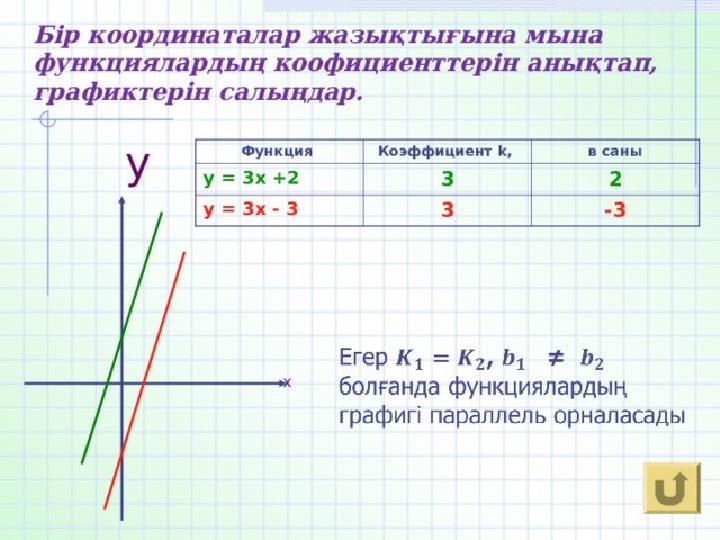
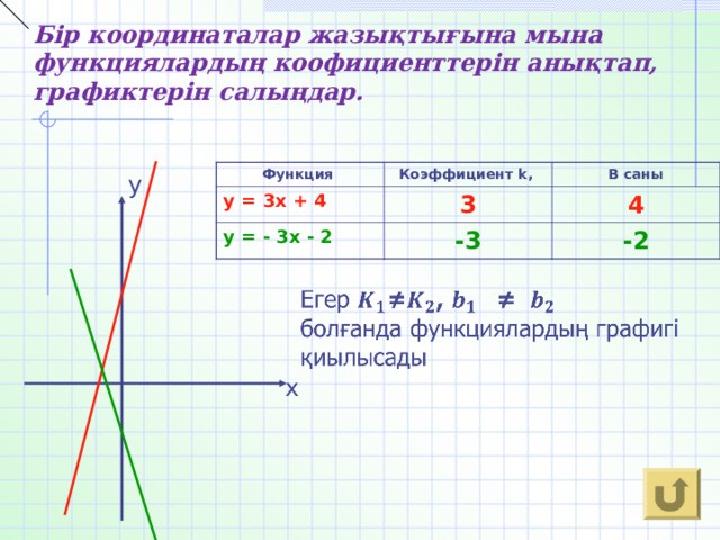
1-мысал. у=2x+1 функциясының графигі мен у=0,5x+4 функциясының графигтерінің қиылысу нүктесін табамыз. Ол үшін 2х+1=0,5х+4 теңдеуінің түбірін табуымыз керек. 2х+1=0,5х+4 2х-0,5х=4-1 1,5х=3 х=2 х=2 болғанда у=2х+1=2*2+1=5; у=5 у=0,5х+4=0,5*2+4; у=5 яғни х=2 болғанда екі функция да 5-ке тең бір ғана мәнді қабылдайды. А (2;5) нүктесі у=2х+1 функциясының графигіне де у=0,5х+4 функциясының графигіне де тиісті болады. Функциялардың графиктері болатын түзулер қиылысады.
#79 слайд
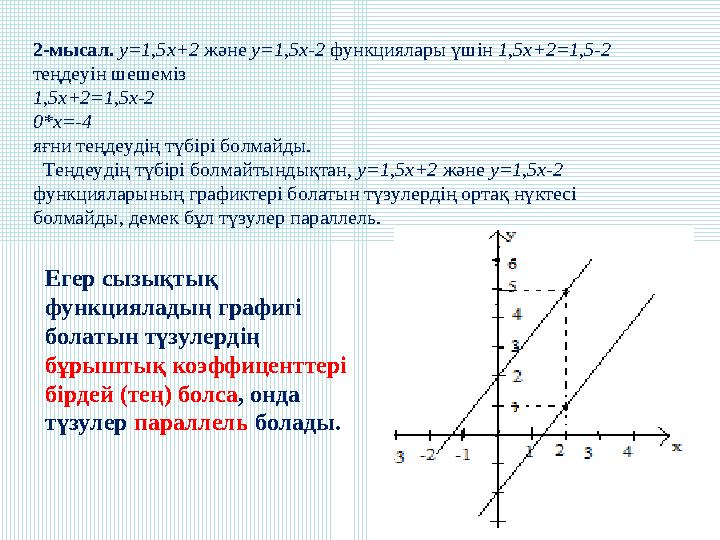
2-мысал. у=1,5х+2 және у=1,5х-2 функциялары үшін 1,5х+2=1,5-2
теңдеуін шешеміз
1,5х+2=1,5х-2
0*х=-4
яғни теңдеудің түбірі болмайды.
Теңдеудің түбірі болмайтындықтан, у=1,5х+2 және у=1,5х-2
функцияларының графиктері болатын түзулердің ортақ нүктесі
болмайды, демек бұл түзулер параллель.
Егер сызықтық
функцияладың графигі
болатын түзулердің
бұрыштық коэффиценттері
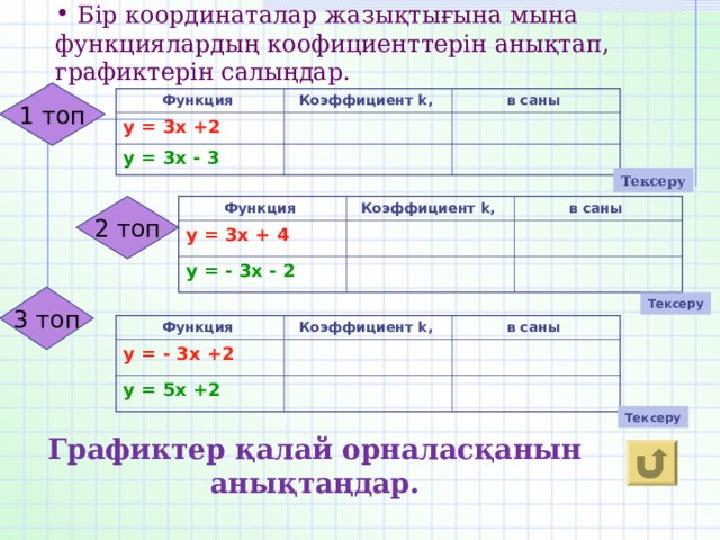
бірдей (тең) болса, онда
түзулер параллель болады.
79 слайд
2-мысал. у=1,5х+2 және у=1,5х-2 функциялары үшін 1,5х+2=1,5-2 теңдеуін шешеміз 1,5х+2=1,5х-2 0*х=-4 яғни теңдеудің түбірі болмайды. Теңдеудің түбірі болмайтындықтан, у=1,5х+2 және у=1,5х-2 функцияларының графиктері болатын түзулердің ортақ нүктесі болмайды, демек бұл түзулер параллель. Егер сызықтық функцияладың графигі болатын түзулердің бұрыштық коэффиценттері бірдей (тең) болса, онда түзулер параллель болады.
#80 слайд
ху
2
1
2
2
1
ху
3
2
1
ху
-
-
-
-
-
80 слайд
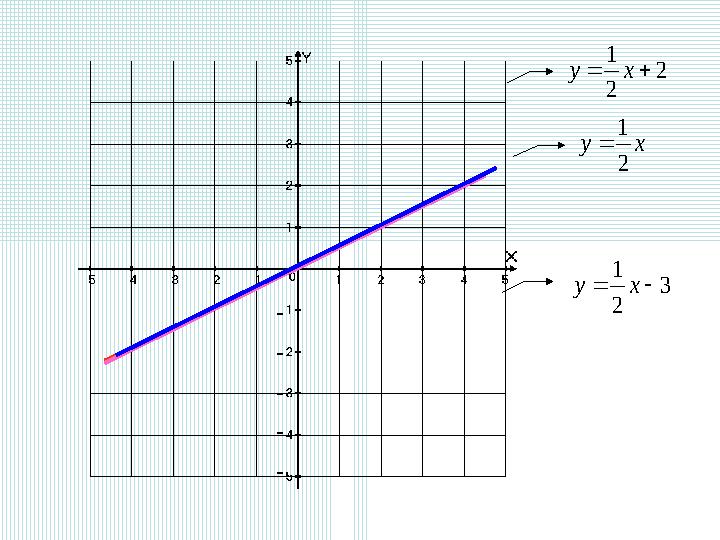
ху 2 1 2 2 1 ху 3 2 1 ху - - - - -

#81 слайд
81 слайд

#82 слайд
82 слайд
#83 слайд
83 слайд

#84 слайд
у = -8х + 11 функциясына параллель және
координатаның бас нүктесі арқылы өтетін
функцияны тап
1.у = -8х + 1
2.у = -8х
3.у = 8х
4.у = 11х
84 слайд
у = -8х + 11 функциясына параллель және координатаның бас нүктесі арқылы өтетін функцияны тап 1.у = -8х + 1 2.у = -8х 3.у = 8х 4.у = 11х

#85 слайд
85 слайд

#86 слайд
Мына функциялардың графиктерін бір
координаталық жазықтықта салыңдар.
уу=-2х+4=-2х+4
у=х+5у=х+5
-2х-4=х+5
-2х-х=5+4
-3х=9
х=-3
у=-2*(-3)-4=6-4=2
А(-3;2)
86 слайд
Мына функциялардың графиктерін бір координаталық жазықтықта салыңдар. уу=-2х+4=-2х+4 у=х+5у=х+5 -2х-4=х+5 -2х-х=5+4 -3х=9 х=-3 у=-2*(-3)-4=6-4=2 А(-3;2)

#87 слайд
Үйге тапсырма Үйге тапсырма
87 слайд
Үйге тапсырма Үйге тапсырма

#88 слайд
Сабақтың тақырыбы:Сабақтың тақырыбы:
Сызықтық функциялардың Сызықтық функциялардың
графиктерінің өзара орналасуыграфиктерінің өзара орналасуы
Сабақтың мақсаты:
7.4.1.8 сызықтық функция графиктерінің өзара
орналасуы олардың коэффициенттеріне тәуелді
болатынын негіздеу
8 сабақ
88 слайд
Сабақтың тақырыбы:Сабақтың тақырыбы: Сызықтық функциялардың Сызықтық функциялардың графиктерінің өзара орналасуыграфиктерінің өзара орналасуы Сабақтың мақсаты: 7.4.1.8 сызықтық функция графиктерінің өзара орналасуы олардың коэффициенттеріне тәуелді болатынын негіздеу 8 сабақ

#89 слайд
Сызықтық функцияның графигі –
түзу, демек, сызықтық
функциялардың графиктері бір
нүктеде қиылысады немесе параллель
болады, немесе беттеседі.
89 слайд
Сызықтық функцияның графигі – түзу, демек, сызықтық функциялардың графиктері бір нүктеде қиылысады немесе параллель болады, немесе беттеседі.

#90 слайд
90 слайд
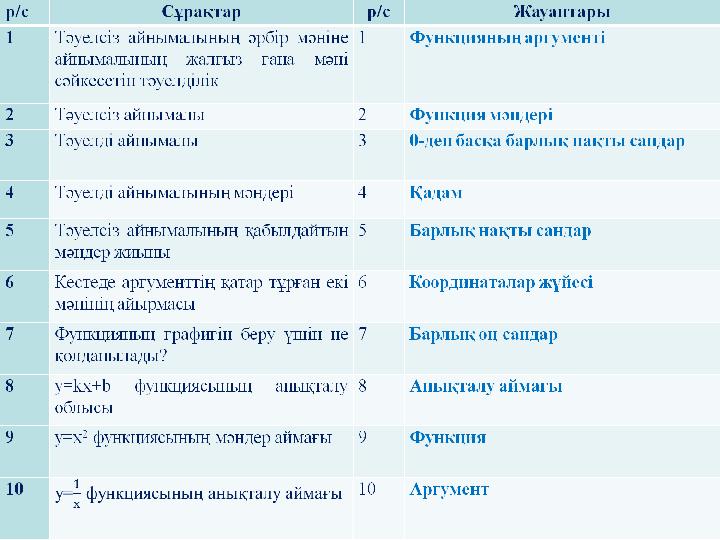
#91 слайд
91 слайд
#92 слайд
92 слайд
#93 слайд
93 слайд
#94 слайд
94 слайд
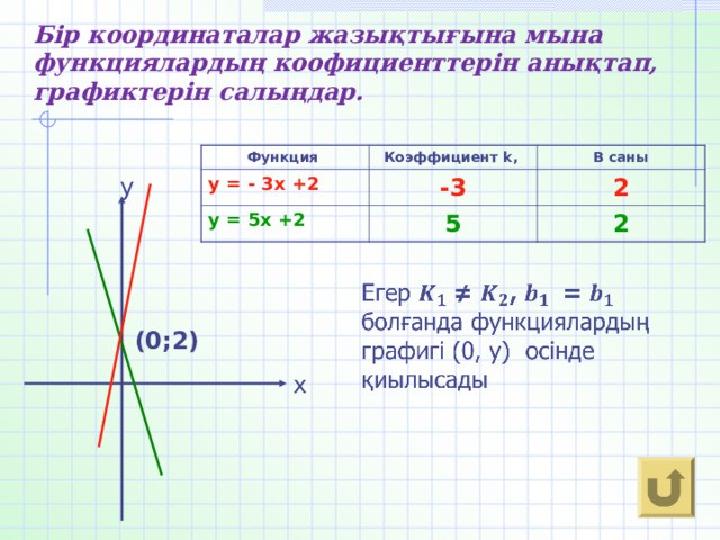
#95 слайд
95 слайд

#96 слайд
96 слайд

#97 слайд
97 слайд

#98 слайд
98 слайд

#99 слайд
99 слайд

#100 слайд
Үйге тапсырма Үйге тапсырма
100 слайд
Үйге тапсырма Үйге тапсырма

#101 слайд
Екі айнымалысы бар сызықтық
теңдеулер жүйесін графиктік
тәсілмен шешу
Сабақтың мақсаты:
7.4.2.4екі айнымалысы бар сызықтық
теңдеулер жүйесін графиктік тәсілмен
шешу
9 сабақ
101 слайд
Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу Сабақтың мақсаты: 7.4.2.4екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу 9 сабақ

#102 слайд
Теңдеулер жүйесі дегеніміз не?
Төмендегі сызықтық функцияларды
қарастырайық :
Y=-x+3 және Y=2x-3
бір мезгілде екі теңдеудің шешімі болатын (x;y)
жұбын табамыз
x=2 және y=1 болғанда екі теңдеуде тура теңдікке
айналады
1 = -2+3 және 1 = 2∙2 -3
Демек , (2; 1) екі теңдеудің ортақ шешімі болып
табылады.
102 слайд
Теңдеулер жүйесі дегеніміз не? Төмендегі сызықтық функцияларды қарастырайық : Y=-x+3 және Y=2x-3 бір мезгілде екі теңдеудің шешімі болатын (x;y) жұбын табамыз x=2 және y=1 болғанда екі теңдеуде тура теңдікке айналады 1 = -2+3 және 1 = 2∙2 -3 Демек , (2; 1) екі теңдеудің ортақ шешімі болып табылады.
#103 слайд
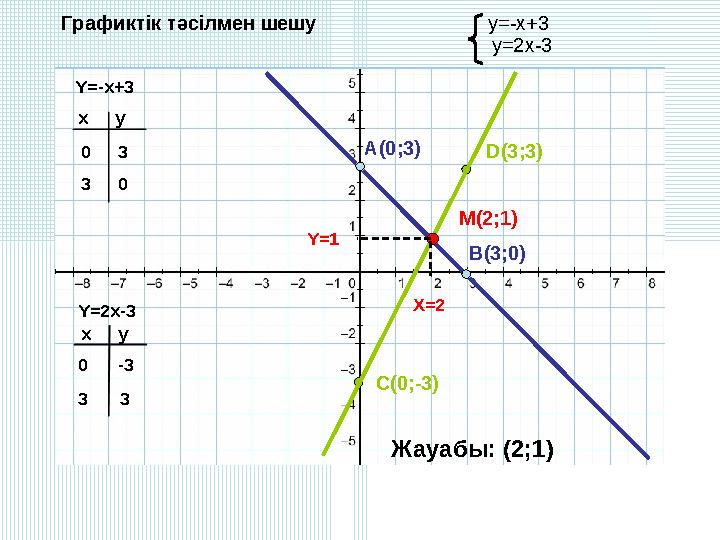
Графиктік тәсілмен шешу y=-x+3
y=2x-3
Y=-x+3
Y=2x-3
xy
0
3
xy
0
3
3
0
-3
3
A(0;3)
B(3;0)
C(0;-3)
D(3;3)
M(2;1)
X=2
Y=1
Жауабы: (2;1)
103 слайд
Графиктік тәсілмен шешу y=-x+3 y=2x-3 Y=-x+3 Y=2x-3 xy 0 3 xy 0 3 3 0 -3 3 A(0;3) B(3;0) C(0;-3) D(3;3) M(2;1) X=2 Y=1 Жауабы: (2;1)
#104 слайд
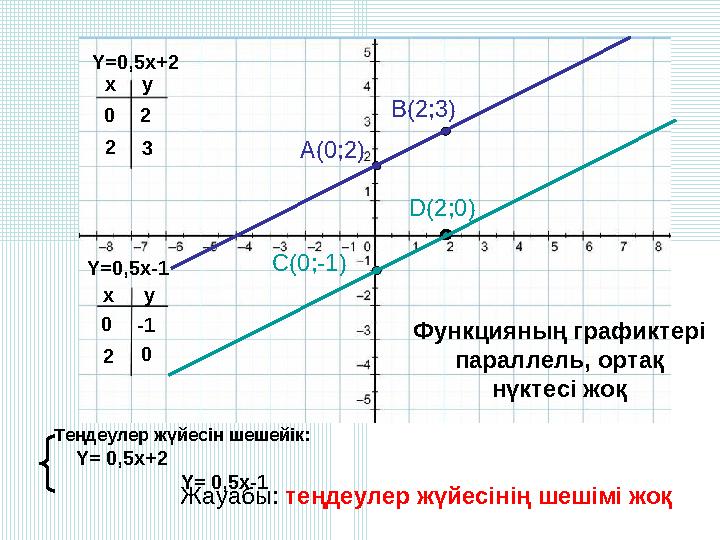
Y=0,5x-1
Y=0,5x+2
x
x
y
y
02
23
0-1
20
A(0;2)
B(2;3)
C(0;-1)
D(2;0)
Теңдеулер жүйесін шешейік:
Y= 0,5x+2
Y= 0,5x-1
Функцияның графиктері
параллель, ортақ
нүктесі жоқ
Жауабы: теңдеулер жүйесінің шешімі жоқ
104 слайд
Y=0,5x-1 Y=0,5x+2 x x y y 02 23 0-1 20 A(0;2) B(2;3) C(0;-1) D(2;0) Теңдеулер жүйесін шешейік: Y= 0,5x+2 Y= 0,5x-1 Функцияның графиктері параллель, ортақ нүктесі жоқ Жауабы: теңдеулер жүйесінің шешімі жоқ
#105 слайд
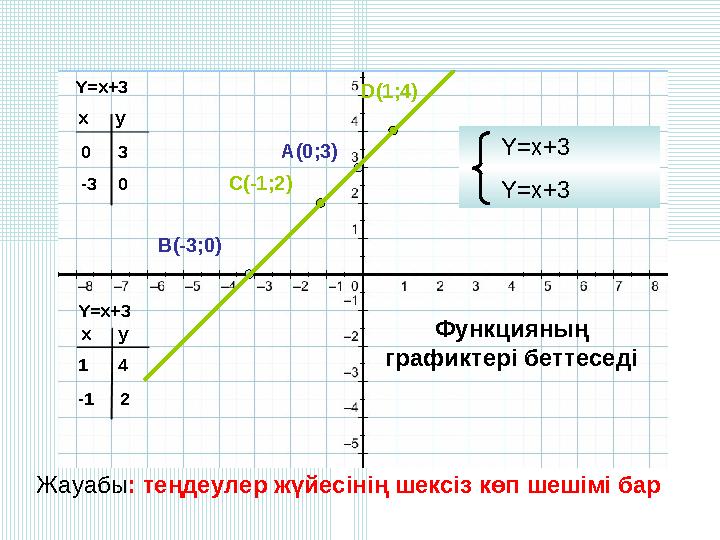
Y=x+3
Y=x+3
xy
0
-3
xy
1
-1
3
0
4
2
A(0;3)
B(-3;0)
C(-1;2)
D(1;4)
Y=x+3
Y=x+3
Функцияның
графиктері беттеседі
Жауабы: теңдеулер жүйесінің шексіз көп шешімі бар
105 слайд
Y=x+3 Y=x+3 xy 0 -3 xy 1 -1 3 0 4 2 A(0;3) B(-3;0) C(-1;2) D(1;4) Y=x+3 Y=x+3 Функцияның графиктері беттеседі Жауабы: теңдеулер жүйесінің шексіз көп шешімі бар
#106 слайд
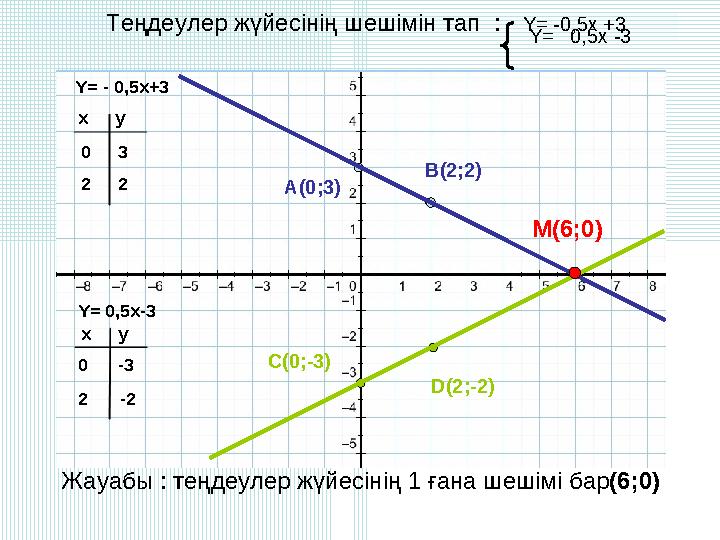
Теңдеулер жүйесінің шешімін тап : Y= -0,5x +3
Y= 0,5x -3
Y= - 0,5x+3
Y= 0,5x-3
xy
0
2
xy
0
2
3
2
-3
-2
A(0;3)
B(2;2)
C(0;-3)
D(2;-2)
M(6;0)
Жауабы : теңдеулер жүйесінің 1 ғана шешімі бар(6;0)
106 слайд
Теңдеулер жүйесінің шешімін тап : Y= -0,5x +3 Y= 0,5x -3 Y= - 0,5x+3 Y= 0,5x-3 xy 0 2 xy 0 2 3 2 -3 -2 A(0;3) B(2;2) C(0;-3) D(2;-2) M(6;0) Жауабы : теңдеулер жүйесінің 1 ғана шешімі бар(6;0)

#107 слайд
107 слайд

#108 слайд
Үйге тапсырма Үйге тапсырма
108 слайд
Үйге тапсырма Үйге тапсырма

#109 слайд
Сабақтың тақырыбы:Сабақтың тақырыбы:
Екі айнымалысы бар сызықтық
теңдеулер жүйесін графиктік тәсілмен
шешу
Сабақтың мақсаты:
7.4.2.4 екі айнымалысы бар сызықтық теңдеулер
жүйесін графиктік тәсілмен шешу
10 сабақ
109 слайд
Сабақтың тақырыбы:Сабақтың тақырыбы: Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу Сабақтың мақсаты: 7.4.2.4 екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу 10 сабақ

#110 слайд
1.Екі айнымалысы бар сызықтық
теңдеу дегеніміз не?
2.Екі айнымалысы бар сызықтық
теңдеудің қасиеттерін айтыңдар.
3.Екі айнымалысы бар сызықтық
теңдеулердің графигі қалай
салынады?
110 слайд
1.Екі айнымалысы бар сызықтық теңдеу дегеніміз не? 2.Екі айнымалысы бар сызықтық теңдеудің қасиеттерін айтыңдар. 3.Екі айнымалысы бар сызықтық теңдеулердің графигі қалай салынады?

#111 слайд
Теңдеулер жүйесін графиктік тәсілмен
шешудің алгоритмі:
1.1.Әр теңдеудің графигін бір Әр теңдеудің графигін бір
координаталар жүйесінде координаталар жүйесінде
салыңызсалыңыз
2. Осы графиктердің қиылысу 2. Осы графиктердің қиылысу
нүктесінің координаталарын нүктесінің координаталарын
анықтаңызанықтаңыз
3. Жауабын (х; у) түрінде жазу3. Жауабын (х; у) түрінде жазу
111 слайд
Теңдеулер жүйесін графиктік тәсілмен шешудің алгоритмі: 1.1.Әр теңдеудің графигін бір Әр теңдеудің графигін бір координаталар жүйесінде координаталар жүйесінде салыңызсалыңыз 2. Осы графиктердің қиылысу 2. Осы графиктердің қиылысу нүктесінің координаталарын нүктесінің координаталарын анықтаңызанықтаңыз 3. Жауабын (х; у) түрінде жазу3. Жауабын (х; у) түрінде жазу
#112 слайд
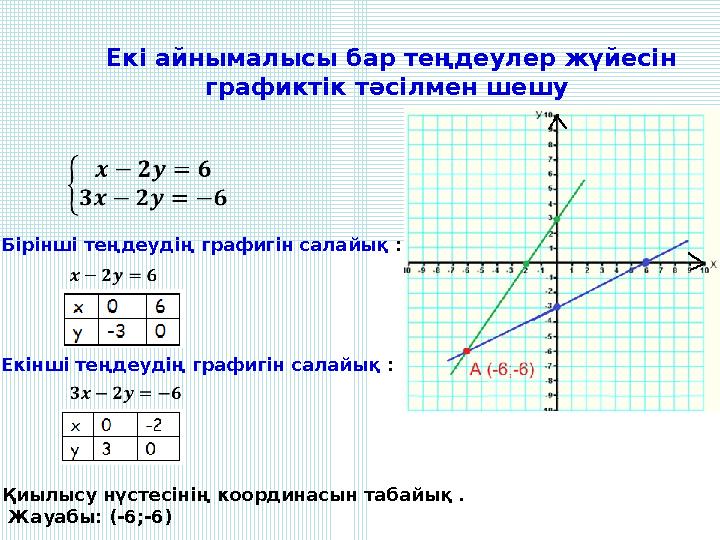
Екі айнымалысы бар теңдеулер жүйесін
графиктік тәсілмен шешу
Бірінші теңдеудің графигін салайық :
Екінші теңдеудің графигін салайық :
Қиылысу нүстесінің координасын табайық .
Жауабы: (-6;-6)
112 слайд
Екі айнымалысы бар теңдеулер жүйесін графиктік тәсілмен шешу Бірінші теңдеудің графигін салайық : Екінші теңдеудің графигін салайық : Қиылысу нүстесінің координасын табайық . Жауабы: (-6;-6)
#113 слайд
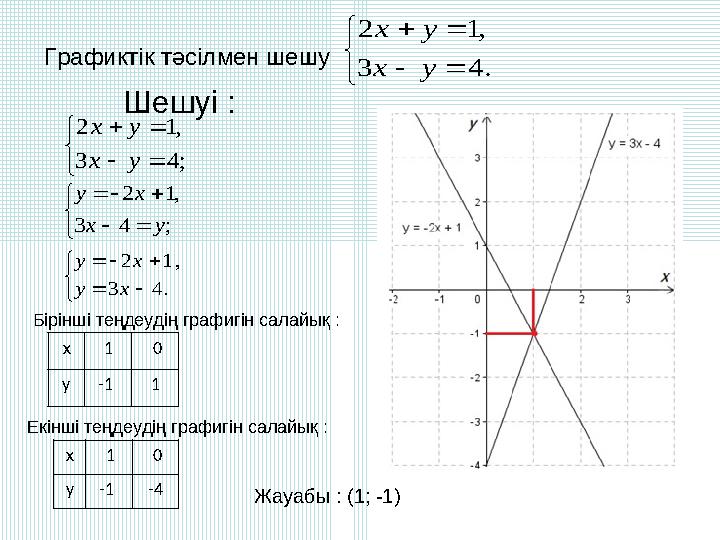
Графиктік тәсілмен шешу
.43
,12
yx
yx
Шешуі :
;43
,12
yx
yx
;43
,12
yx
xy
.43
,12
xy
xy
Бірінші теңдеудің графигін салайық :
x1 0
y -11
Екінші теңдеудің графигін салайық :
x 1 0
y -1-4
Жауабы : (1; -1)
113 слайд
Графиктік тәсілмен шешу .43 ,12 yx yx Шешуі : ;43 ,12 yx yx ;43 ,12 yx xy .43 ,12 xy xy Бірінші теңдеудің графигін салайық : x1 0 y -11 Екінші теңдеудің графигін салайық : x 1 0 y -1-4 Жауабы : (1; -1)
#114 слайд
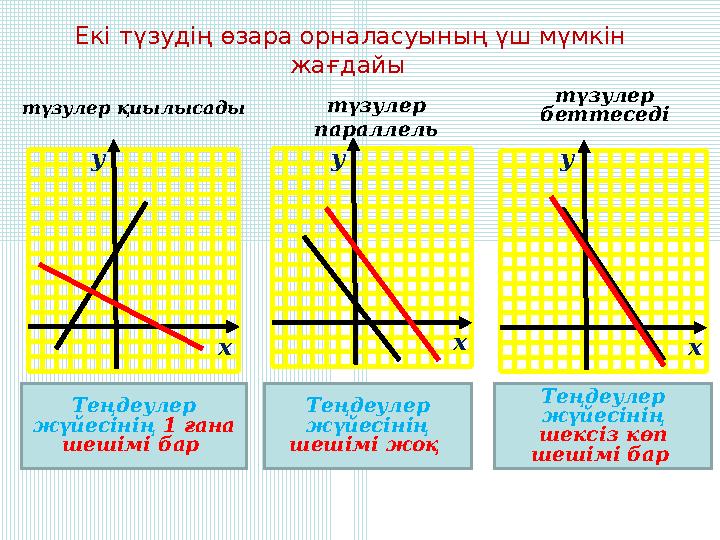
Екі түзудің өзара орналасуының үш мүмкін
жағдайы
түзулер
параллель
түзулер
беттеседі
Теңдеулер
жүйесінің 1 ғана
шешімі бар
Теңдеулер
жүйесінің
шешімі жоқ
Теңдеулер
жүйесінің
шексіз көп
ш...
114 слайд
Екі түзудің өзара орналасуының үш мүмкін жағдайы түзулер параллель түзулер беттеседі Теңдеулер жүйесінің 1 ғана шешімі бар Теңдеулер жүйесінің шешімі жоқ Теңдеулер жүйесінің шексіз көп ш...

шағым қалдыра аласыз
















