Айнымалы ток

1 слайд
Айнымалы ток тізбегіндегі актив кедергі R кедергіні айнымалы ток тізбегіндегі активті кедергі деп атайды. Айнымалы ток күшінің лездік мәні ( ) синусоидалық заңға сәйкес белгілі бір уақыт ішінде мынадай заң бойынша өзгереді: Сондай жиіліктегі кернеу де синусоидалық заң бойынша өзгереді: Мұндай айнымалы токтың әсерлік мәндері мынаған тең болады: Тек активт і кедергісі бар тізбектегі айнымалы токтың бір период ішіндегі орташа қуаты әсерлік ток мәні мен әсерлік кернеу мәнінің көбейтіндісінен кем болады: .2 2 m I R p  2 p I R 

1 слайд

2 слайд
Айнымалы ток тізбегіндегі индуктивті кедергіcos( ) sin( ) 2 L m m dI L LI t LI t dt               Айнымалы ток т ізбегінде катушка индуктивті қосымша кедергі тудырады. Катушкада лездік мәні болатын өздік индукцияның ЭҚК-і пайда болады. Өздік индукцияның ЭҚК-і ток өзгерісіне кері әсер етеді, сондықтан тек индуктивтілік бар тізбекте ток фаза бойынша кернеуден ширек периодқа, яғни -ге қалыс қалады. Катушкадағы ток күшінің амплитудасы - идеал катушкасы бар айнымалы ток тізбегі үшін Ом заңы - катушканың индуктивті кедергісі 2 

2 слайд

3 слайд
Айнымалы ток тізбегіндегі сыйымдылық кедергі Конденсаторды айнымалы кернеу көзіне қосса, ол үнемі қайта зарядталып отырады да тізбек арқылы ток жүреді. Сыйымдылық C шамасы U -ге тең кернеуге қосылғанда, оның заряды: Периодты түрде өзгеріп отыратын кернеу периодты түрде өзгеретін зарядты тудырады да,сыйымдылық тогы пайда болады: Ток күшінің амплитудасы Сыйымдылық кедергі q CU  cos( ) sin( ) 2 m m dq dU I C CU t CU t dt dt               m m m c U I CU X    1 c X C  

3 слайд

4 слайд
Айнымалы токтың толық тізбегі үшін Ом заңы Бір-біріне тізбектей жалғанған индуктивтігі L катушкадан, сыйымдылығы С конденсатордан және кедергісі R резистордан тұратын тізбекті айнымалы токтың толық тізбегі деп атайды. Түсірілген кернеудің амплитудасын Барлық тізбектегі кернеудің амплитудасы Пифагор теоремасы бойынша Ом заңына сәйкесR L C U U U U    mR mL mC m U U U U    АААААААААААААААААААААААААААААААААААААААААААААААААААААААА 2 2 ( ) m mR mL mC U U U U    2 2 2 2 2 ( ) ( ) m m m L m c m L c U I R I X I X I R X X      

4 слайд

5 слайд
Айнымалы токтың толық тізбегі үшін Ом заңы2 2 ( 1 / ) m m U I R L C      2 2 ) / 1 ( C L R Z      Импеданс ( толық кедергі ) C L X   / 1   - реактивті кедергі 2 2 , , / 1 , X R Z X X X C X L X C L C L         Индуктивті кедергі Сиымдылықты кедергі 1 / L C X X L C tg R R        mL mC mR U U tg U   

5 слайд

6 слайд
Кернеу резонансы. Резонанстық жиілік .2 2 ) / 1 ( C L R Z      1 L C    Егер индуктивті кедергі мен сыйымдылық кедергі бір-біріне тең болса, толық кедергі ең аз мәнге ие болады. Мұндай жағдайда ток пен кернеудің тербеліс фазаларының айырымы Ом заңы бойынша ток амплитудасы Резонанс байқалу үшін тізбекке түсірілген кернеудің жиілігі - Томсон формуласы Z R  1 / 0 L C tg R       m m m U U I Z R   1 рез LC   2 T LC  

6 слайд

7 слайд
Айнымалы ток тізбегінде бөлінетін қуат) cos( cos ) (       t t I U UI t P m m       sin sin cos cos ) cos( t t t    ) sin cos sin cos (cos ) ( 2      t t t I U t P m m   0 cos sin , 2/ 1 cos 2       t t t    Қуаттың лездік мәні Қуаттың тербеліс периоды бойынша орташа мәні  cos 2 m m I U P    m m RI U   cos (векторлық диаграммадан) 2 / 2 m RI P    2 / , 2 / m m U U I I   Барлық амперметрлер мен вольтметрлер осы мән бойынша көрсетеді  cos UI P    Қуат коэффициентіАйнымалы ток тізбегіндегі орташа қуат

7 слайд

8 слайд
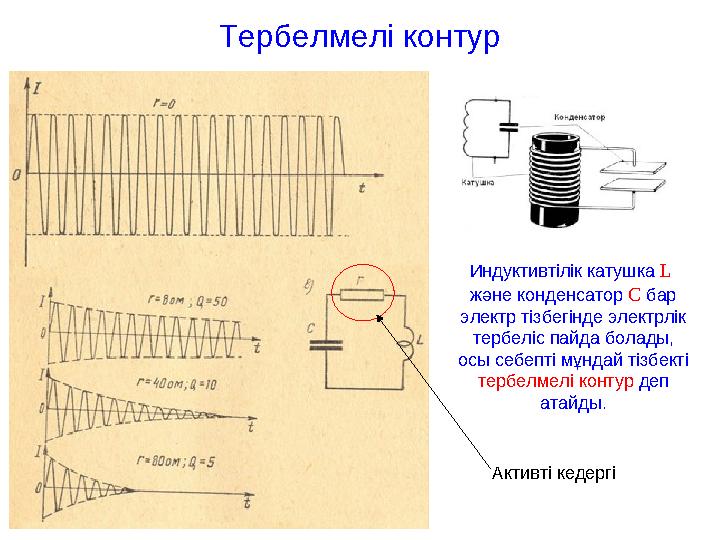
Тербелмелі контур Индуктивтілік катушка L және конденсатор C бар электр тізбегінде электрлік тербеліс пайда болады, осы себепті мұндай тізбекті тербелмелі контур деп атайды. Активті кедергі

8 слайд

9 слайд
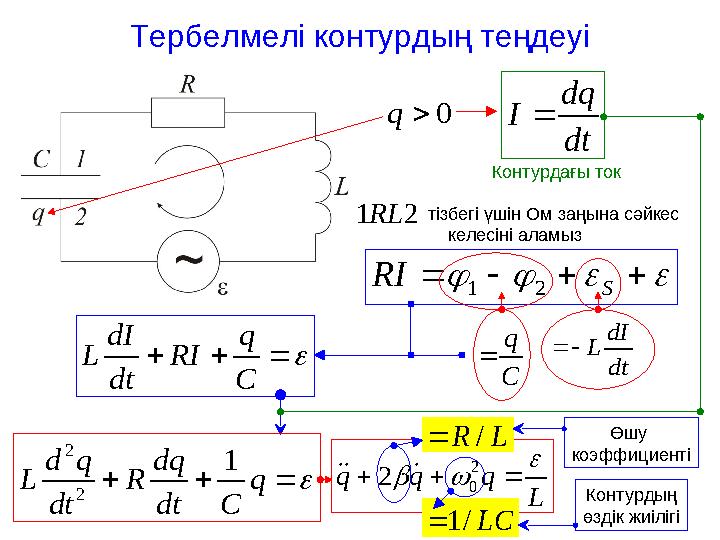
Тербелмелі контурдың теңдеуі0  q dt dq I  2 1 RL Контурдағы ток тізбегі үшін Ом заңына сәйкес келесіні аламыз         S RI 2 1 dt dI L   C q      C q RI dt dI L     q C dt dq R dt q d L 1 2 2 L q q q       2 0 2   L R /  LC / 1  Өшу коэффициенті Контурдың өздік жиілігі

9 слайд

10 слайд
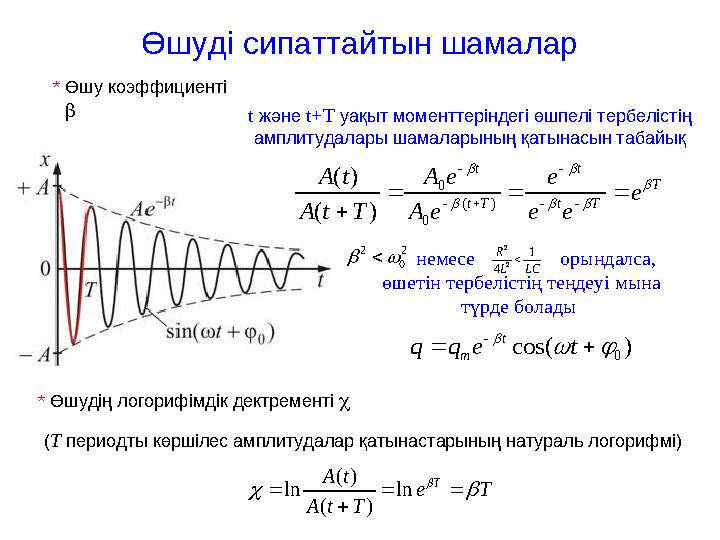
Өшуді сипаттайтын шамалар * Өшу коэффициенті T T t t T t t e e e e e A e A T t A t A                 ) ( 0 0 ) ( ) ( t және t+T уақыт моменттеріндегі өшпелі тербелістің амплитудалары шамаларының қатынасын табайық * Өшудің логорифімдік дектременті  ( T периодты көршілес амплитудалар қатынастарының натураль логорифмі) ( ) ln ln ( ) T A t e T A t T        немесе орындалса, өшетін тербелістің теңдеуі мына түрде болады 2 2 0    2 2 1 4 R L LC  0 cos( ) t m q q e t      

10 слайд