Ашык сабақ
Ашык сабақ


#1 слайд
Антоновка №23 негізгі мектебі
Тақырыбы:
Квадрат теңдеулерді шешу тәсілдері
Математика пәнінің мұғалімі
Табигат.А
1 слайд
Антоновка №23 негізгі мектебі Тақырыбы: Квадрат теңдеулерді шешу тәсілдері Математика пәнінің мұғалімі Табигат.А

#2 слайд
Мақсаты:
Қазіргі жастар - ол ертеңгі ұлттың үміті, жас
ұрпақты әлеуметтік белсенділікке,
жауапкершілікке, тиянақтылыққа, туған халқының
тарихын, мәдениетін жетістіктерін құрметтей
білуге тәрбиелеу болып табылады.
Білім беру үдерісінде мүмкіндігінше кеңірек
қарап, әр оқушыны қазіргі заманғы әлемде
білімділікке, Отан мен халыққа қызмет етуге, оның
қадір - қасиетін ұғынуға тәрбиелеу.
2 слайд
Мақсаты: Қазіргі жастар - ол ертеңгі ұлттың үміті, жас ұрпақты әлеуметтік белсенділікке, жауапкершілікке, тиянақтылыққа, туған халқының тарихын, мәдениетін жетістіктерін құрметтей білуге тәрбиелеу болып табылады. Білім беру үдерісінде мүмкіндігінше кеңірек қарап, әр оқушыны қазіргі заманғы әлемде білімділікке, Отан мен халыққа қызмет етуге, оның қадір - қасиетін ұғынуға тәрбиелеу.

#3 слайд
ЖОСПАР:
І. Кіріспе.
Білім сапасын көтеруге мұғалімінің атқаратын міндеті
ІІ.Негізгі бөлімі.
1.Толымсыз квадрат теңдеулерді шешу.
2.Квадрат теңдеулерді формулалар арқылы шешу.
3.Квадрат теңдеулерді екінші коэффициенті жұп
сан болған жағдайдағы шешу формуласы.
4. Квадрат теңдеулерді Виет теоремасы
арқылы шешу.
5.Виет теоремасына кері теорема
ІІІ. Қорытынды.
3 слайд
ЖОСПАР: І. Кіріспе. Білім сапасын көтеруге мұғалімінің атқаратын міндеті ІІ.Негізгі бөлімі. 1.Толымсыз квадрат теңдеулерді шешу. 2.Квадрат теңдеулерді формулалар арқылы шешу. 3.Квадрат теңдеулерді екінші коэффициенті жұп сан болған жағдайдағы шешу формуласы. 4. Квадрат теңдеулерді Виет теоремасы арқылы шешу. 5.Виет теоремасына кері теорема ІІІ. Қорытынды.

#4 слайд
Елбасымыз Н.Ә.Назарбаев Қазақстан халқына
жолдауында Қазақстанның әлемдегі барынша қабілетті
елу елдің қатарына кіруінде білім сапасы жоғары,
денсаулығы мықты, еліміздің әл-ауқаты үшін қызмет
жасайтын жастарға үлкен сенім білдіріп отыр.
4 слайд
Елбасымыз Н.Ә.Назарбаев Қазақстан халқына жолдауында Қазақстанның әлемдегі барынша қабілетті елу елдің қатарына кіруінде білім сапасы жоғары, денсаулығы мықты, еліміздің әл-ауқаты үшін қызмет жасайтын жастарға үлкен сенім білдіріп отыр.

#5 слайд
Қайталау сұрақтары:
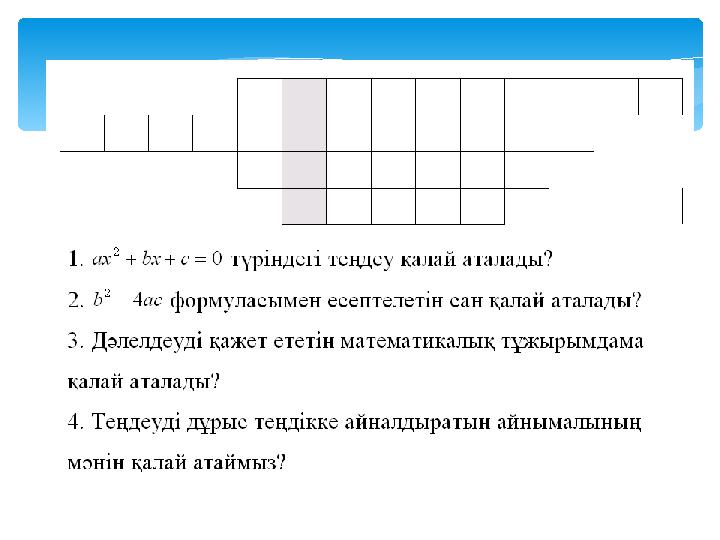
1. түріндегі теңдеу қалай аталады?
2. формуласымен есептелетін сан қалай
аталады?
3. Егер D>0 болса, онда квадраттық теңдеудің неше түбірі
болады?
4. Егер D=0 болса, онда квадраттық теңдеудің неше түбірі
болады?
5. Егер D<0 болса, онда квадраттық теңдеудің неше түбірі болады?
6. Қандай жағдайда квадраттық теңдеу келтірілген квадраттық
теңдеу деп атайды?
7. теңдеуінің коэффициенттерін атап
шығыңдар.
8. Егер квадраттық теңдеуінде коэффициенттердің бірі – b не с
немесе b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді
қалай атайды?
0
2
cbxах
acb4
2
0352
2
хх
5 слайд
Қайталау сұрақтары: 1. түріндегі теңдеу қалай аталады? 2. формуласымен есептелетін сан қалай аталады? 3. Егер D>0 болса, онда квадраттық теңдеудің неше түбірі болады? 4. Егер D=0 болса, онда квадраттық теңдеудің неше түбірі болады? 5. Егер D<0 болса, онда квадраттық теңдеудің неше түбірі болады? 6. Қандай жағдайда квадраттық теңдеу келтірілген квадраттық теңдеу деп атайды? 7. теңдеуінің коэффициенттерін атап шығыңдар. 8. Егер квадраттық теңдеуінде коэффициенттердің бірі – b не с немесе b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді қалай атайды? 0 2 cbxах acb4 2 0352 2 хх
#6 слайд
0
2
ах
,0
2
сах
мұндағы
0с
,0
2
bxах
0b
мұндағы
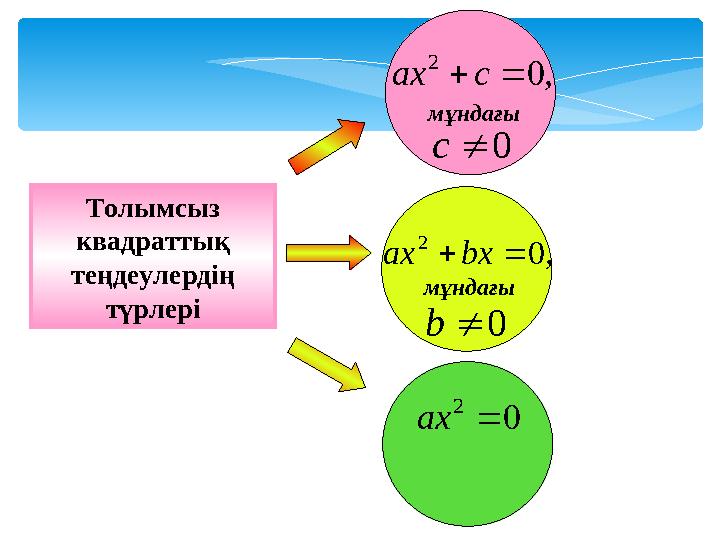
Толымсыз
квадраттық
теңдеулердің
түрлері
6 слайд
0 2 ах ,0 2 сах мұндағы 0с ,0 2 bxах 0b мұндағы Толымсыз квадраттық теңдеулердің түрлері
#7 слайд
0
2
ах
сах
2
а
с
х
2
0
а
с
екі түбірі
болады
0
а
с
түбірлері
жоқ
0)( baxx
0х немесе
0bах
bах
a
b
х
екі түбірі болады
0
2
ах
0
2
х
0х
бір ғана түбірі
болады
,0
2
сах
0с
мұндағы
,0
2
bxах
0b
мұндағы
7 слайд
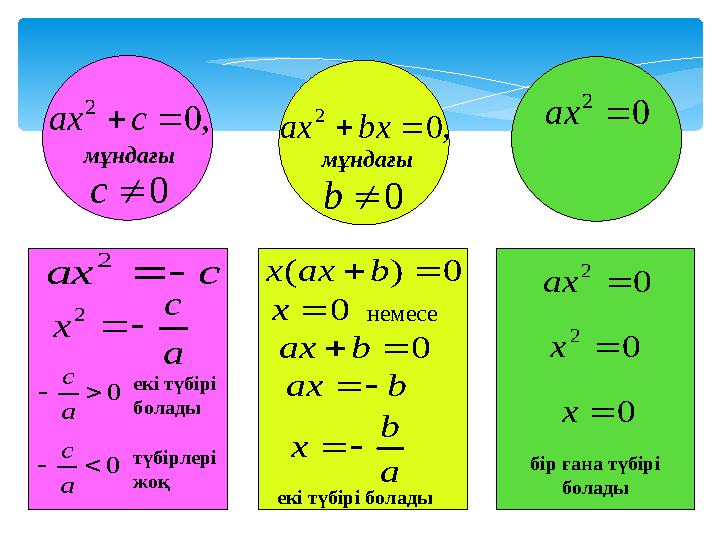
0 2 ах сах 2 а с х 2 0 а с екі түбірі болады 0 а с түбірлері жоқ 0)( baxx 0х немесе 0bах bах a b х екі түбірі болады 0 2 ах 0 2 х 0х бір ғана түбірі болады ,0 2 сах 0с мұндағы ,0 2 bxах 0b мұндағы

#8 слайд
Бұл мысалдардан, келтірілген квадраттық теңдеу
түбірлерінің қосындысы қарсы таңбасымен алынған
екінші коэффициентке, ал көбейтіндісі бос мүшеге
тең екенін байқадық.
Енді бұл қасиетті теорема ретінде тұжырымдап
шығайық.
Теорема : Келтірілген квадраттық теңдеу
түбірлерінің қосындысы қарсы таңбасымен
алынған екінші коэффициентке, ал көбейтіндісі
бос мүшеге тең болады:
qxxpхх
2121 ;
8 слайд
Бұл мысалдардан, келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең екенін байқадық. Енді бұл қасиетті теорема ретінде тұжырымдап шығайық. Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады: qxxpхх 2121 ;

#9 слайд
(келтірілген квадрат
теңдеу)
– екінші коэффициент
– бос мүше
Теңдеудің дискриминанті:
Егер D>0, онда теңдеудің екі түбірі бар:
және
Түбірлердің қосындысы:
Түбірлердің көбейтіндісі:
.
Сонымен,
2
1
Dр
х
2
2
Dр
х
p
pDрDр
хх
2
2
2
21
4
)()(
22
)()(
22
21
DpDрDр
хх
q
qppDp
4
)4(
4
222
0
2
qpxx
p
q
qpD 4
2
pхх
21
qхх
21
9 слайд
(келтірілген квадрат теңдеу) – екінші коэффициент – бос мүше Теңдеудің дискриминанті: Егер D>0, онда теңдеудің екі түбірі бар: және Түбірлердің қосындысы: Түбірлердің көбейтіндісі: . Сонымен, 2 1 Dр х 2 2 Dр х p pDрDр хх 2 2 2 21 4 )()( 22 )()( 22 21 DpDрDр хх q qppDp 4 )4( 4 222 0 2 qpxx p q qpD 4 2 pхх 21 qхх 21

#10 слайд
Бұл мысалдардан, келтірілген квадраттық теңдеу
түбірлерінің қосындысы қарсы таңбасымен алынған
екінші коэффициентке, ал көбейтіндісі бос мүшеге
тең екенін байқадық.
Енді бұл қасиетті теорема ретінде тұжырымдап
шығайық.
Теорема : Келтірілген квадраттық теңдеу
түбірлерінің қосындысы қарсы таңбасымен
алынған екінші коэффициентке, ал көбейтіндісі
бос мүшеге тең болады:
qxxpхх
2121 ;
10 слайд
Бұл мысалдардан, келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең екенін байқадық. Енді бұл қасиетті теорема ретінде тұжырымдап шығайық. Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады: qxxpхх 2121 ;

#11 слайд
Бұл теореманы бірінші дәлелдеген француз математигі
Француа Виет (1540-1603) болғандықтан, соның
атымен аталады.
Кейбір есептерді шешкенде Виет теоремасына кері
теореманы қолданады.
Теорема (кері теорема). Егер сандары
үшін шарттары орындалса,
онда сандары
теңдеуінің түбірлері болады.
21
,,, xxqp
qxxpхх
2121 ,
21
xменx 0
2
qpxх
11 слайд
Бұл теореманы бірінші дәлелдеген француз математигі Француа Виет (1540-1603) болғандықтан, соның атымен аталады. Кейбір есептерді шешкенде Виет теоремасына кері теореманы қолданады. Теорема (кері теорема). Егер сандары үшін шарттары орындалса, онда сандары теңдеуінің түбірлері болады. 21 ,,, xxqp qxxpхх 2121 , 21 xменx 0 2 qpxх

#12 слайд
Виет теоремасы және оған кері теорема теңдеуді
шешпей-ақ , түбірлерінің қосындысы мен
көбейтіндісін табуға және түбірлері белгілі болғанда,
теңдеуді құруға мүмкіндік береді.
Мысал қарастырайық:
Түбірлері және
болған квадраттық теңдеуді құрайық:
32
1õ 32
2
õ
0)32)(32()3232(
2
õõ
014
2
õõ
12 слайд
Виет теоремасы және оған кері теорема теңдеуді шешпей-ақ , түбірлерінің қосындысы мен көбейтіндісін табуға және түбірлері белгілі болғанда, теңдеуді құруға мүмкіндік береді. Мысал қарастырайық: Түбірлері және болған квадраттық теңдеуді құрайық: 32 1õ 32 2 õ 0)32)(32()3232( 2 õõ 014 2 õõ
#13 слайд
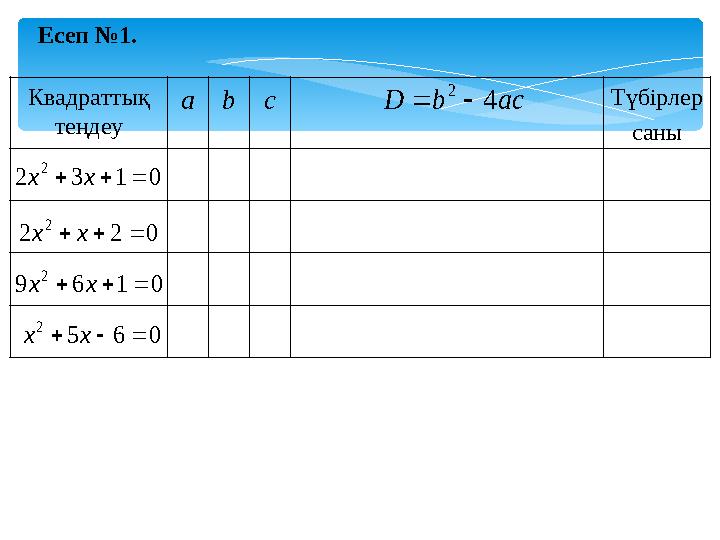
Есеп №1.
Квадраттық
теңдеу
abc Түбірлер
саны
0132
2
xх
022
2
xх
0169
2
xх
065
2
xх
acbD 4
2
13 слайд
Есеп №1. Квадраттық теңдеу abc Түбірлер саны 0132 2 xх 022 2 xх 0169 2 xх 065 2 xх acbD 4 2
#14 слайд
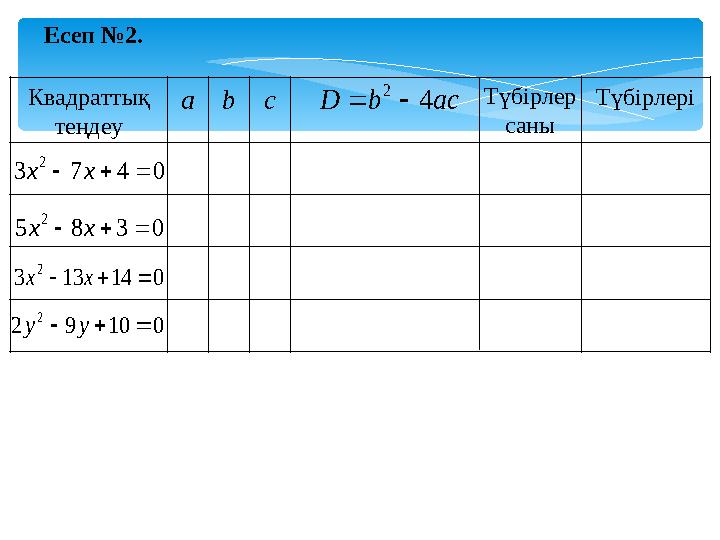
Есеп №2.
Квадраттық
теңдеу
abc ТүбірлеріacbD 4
2
Түбірлер
саны
0473
2
xх
0385
2
xх
014133
2
xх
01092
2
уу
14 слайд
Есеп №2. Квадраттық теңдеу abc ТүбірлеріacbD 4 2 Түбірлер саны 0473 2 xх 0385 2 xх 014133 2 xх 01092 2 уу

#15 слайд
Түбірлері бар бірнеше келтірілген квадраттық
теңдеудің түбірлерін, түбірлерінің қосындысы мен
көбейтіндісінің мәндерін табыңдар және
жауаптарын кестеге толтырыңдар.
Теңдеулер Түбірлер
х
1
және х
2
х
1+ х
2х
1 · х
2
х
2
– 2х – 3 = 0
Х
2
+ 5х – 6 = 0
х
2
– х – 12 = 0
15 слайд
Түбірлері бар бірнеше келтірілген квадраттық теңдеудің түбірлерін, түбірлерінің қосындысы мен көбейтіндісінің мәндерін табыңдар және жауаптарын кестеге толтырыңдар. Теңдеулер Түбірлер х 1 және х 2 х 1+ х 2х 1 · х 2 х 2 – 2х – 3 = 0 Х 2 + 5х – 6 = 0 х 2 – х – 12 = 0

#16 слайд
Теңдеулер Түбірлерінің
қосындысы
Түбірлерінің
көбейтіндісі
0352
2
хх
034
2
хх
078
2
хх
098
2
хх
№257
16 слайд
Теңдеулер Түбірлерінің қосындысы Түбірлерінің көбейтіндісі 0352 2 хх 034 2 хх 078 2 хх 098 2 хх №257
#17 слайд
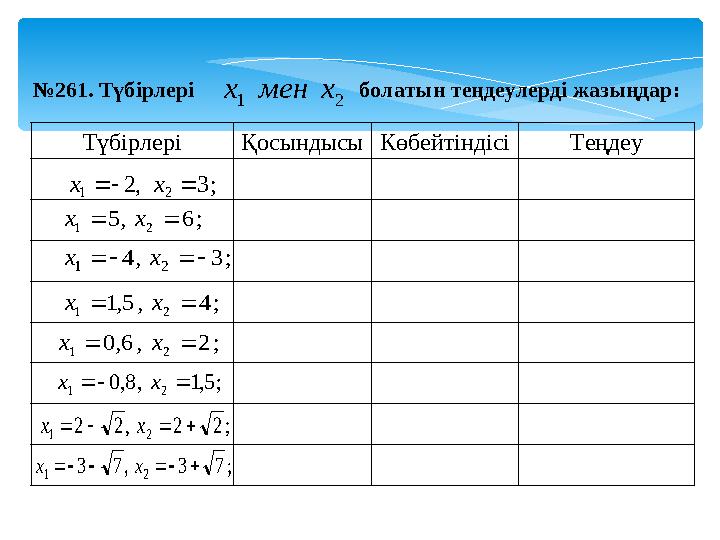
№261. Түбірлері болатын теңдеулерді жазыңдар:
21
хменх
;3,2
21 хх
Түбірлері ҚосындысыКөбейтіндісіТеңдеу
;6,5
21
хх
;3,4
21
хх
;4,5,1
21
хх
;2,6,0
21
хх
;5,1,8,0
21
хх
;22,22
21
хх
;73,73
21
хх
17 слайд
№261. Түбірлері болатын теңдеулерді жазыңдар: 21 хменх ;3,2 21 хх Түбірлері ҚосындысыКөбейтіндісіТеңдеу ;6,5 21 хх ;3,4 21 хх ;4,5,1 21 хх ;2,6,0 21 хх ;5,1,8,0 21 хх ;22,22 21 хх ;73,73 21 хх

#18 слайд
Тест тапсырмалары
1. Теңдеуді шешіңіз:
2. Теңдеуді шешіңіз:
3. Теңдеуді шешіңіз:
4. Теңдеуді шешіңіз:
5. Теңдеуді шешіңіз:
6. Теңдеуді шешіңіз:
094
2
х
А) 0; 1,5. В) -1,5; 1,5. С) -1,5; 0. D) 0. Е) 1,5.
065
2
хх
А) 0; 1,2. В) -1,2; 1,2. С) -1,2; 0. D) 0. Е) -1,2.
02
2
х
А) 0; 2. В) -2; 2. С) -2; 0. D) 0. Е) 2.
067
2
хх
А) 1; 6. В) 4; 5. С) 4; 7. D) -5; 2. Е) -1; 2.
012
2
хх
А) 1. В) -1; 0. С) -1; 1. D) -1. Е) 0.
015
2
хх
А) -1; 0. В) Түбірлері жоқ. С) 1. D) -1. Е) 0.
18 слайд
Тест тапсырмалары 1. Теңдеуді шешіңіз: 2. Теңдеуді шешіңіз: 3. Теңдеуді шешіңіз: 4. Теңдеуді шешіңіз: 5. Теңдеуді шешіңіз: 6. Теңдеуді шешіңіз: 094 2 х А) 0; 1,5. В) -1,5; 1,5. С) -1,5; 0. D) 0. Е) 1,5. 065 2 хх А) 0; 1,2. В) -1,2; 1,2. С) -1,2; 0. D) 0. Е) -1,2. 02 2 х А) 0; 2. В) -2; 2. С) -2; 0. D) 0. Е) 2. 067 2 хх А) 1; 6. В) 4; 5. С) 4; 7. D) -5; 2. Е) -1; 2. 012 2 хх А) 1. В) -1; 0. С) -1; 1. D) -1. Е) 0. 015 2 хх А) -1; 0. В) Түбірлері жоқ. С) 1. D) -1. Е) 0.
#19 слайд
19 слайд

#20 слайд
Сабақ – ұстаздың көп ізденуінен, көп
еңбектенуінен туатын педагогикалық
шығарма. Ал осы «шығарманы» алдында
отырған оқушыларға игерту де оңай шаруа
емес. Ол үшін мұғалімнің біліктілігі,
іскерлігі, көптеген әдіс-тәсілдерді қолдана
білуі, айтқанын оқушы жүрегіне жеткізе
алатындай шешендігі, шебер ой-өрнегі болуы
керек.
Қорытынды
20 слайд
Сабақ – ұстаздың көп ізденуінен, көп еңбектенуінен туатын педагогикалық шығарма. Ал осы «шығарманы» алдында отырған оқушыларға игерту де оңай шаруа емес. Ол үшін мұғалімнің біліктілігі, іскерлігі, көптеген әдіс-тәсілдерді қолдана білуі, айтқанын оқушы жүрегіне жеткізе алатындай шешендігі, шебер ой-өрнегі болуы керек. Қорытынды

#21 слайд
Назарларыңызға
рахмет!
Жұмыстарыңызға
сәттілік тілеймін!
21 слайд
Назарларыңызға рахмет! Жұмыстарыңызға сәттілік тілеймін!

шағым қалдыра аласыз
















