Ашық сабақ

1 слайд
МАТЕМАТИКА 4 “А” СЫНЫП

1 слайд

2 слайд

2 слайд

3 слайд
Сабақтың мақсаты: Қос теңсіздіктермен танысамыз және шешімдер жиынын табуды үйренеміз. Бүгінгі сабақта үйренетін жаңа терминдер, ережелер Қос теңсіздік. Шешімдер жиыны. Қос теңсіздік дегеніміз бір жолға жазылған екі теңсіздік. Жаңа сабақты түсініп алуға тырыс

3 слайд

4 слайд
Жаңа сабақ. Қос теңсіздіктер. Түсіндірме жұмысы. Теңсіздік дегеніміз не? Есімізге түсірейік. «<» немесе «>»белгілерімен біріктірілген санды өрнектер не екі саны бар жазу теңсіздік деп аталады. Теңсіздікті шешу-барлық әріптерінің сан мәндерін табу. Мәндерін орнына қою кезінде теңсіздік тура санды теңсіздікке айналады. Ал бүгінгі сабақта қос теңсіздіктермен танысамыз және оның шешімдер жиынын табуды үйренеміз. Шешімдер жиынын сандық сәуледе қалай белгіленетінімен танысамыз. Қос теңсіздікпен таныспас бұрын теңсіздіктердің шешімдер жиынын жазып, оны сан сәулесінде қалай белгіленетіндігіне зер салайық. Мысалы: Екі сәуле салдық және бірінші сәуленің бойына х < 8 теңсіздігінің шешімдерін, ал екінші сәуленің бойына х > 2 теңсіздігінің шешімдерін белгіледік. Бірінші сәуледе х < 8 теңсіздігінің шешімдері 8-ден кем сандар. Екінші сәуледе х > 2 теңсіздігінің шешімдері 2-ден артық сандар. x > 2 теңсіздігінің шешімі – бұл А жиынының элементтері: А = {3, 4, 5,6, 7, 8, 9, 10, ...}, х < 8 теңсіздігінің шешімі – бұл В жиынының элементтері: В= { 0,1, 2, 3, 4, 5, 6, 7}. Осы екі теңсіздіктен қос теңсіздік құрамыз.

4 слайд

5 слайд
Ал қос теңсіздік деген не? Қос теңсіздік дегеніміз бір жолға жазылған екі теңсіздік. х < 8 және х > 2 теңсіздіктер шешімдерінің жиынын фигуралық жақша, теңдік таңбасы және жиындардың белгіленуі көмегімен жазады. Қос теңсіздік түрінде былайша жазады: 2 < х < 8 Бір сәуленің бойына алдымен х < 8 және х > 2 теңсіздіктерінің шешімдерін, содан соң 2 < х < 8 қос теңсіздігінің шешімдерін белгілеймыз. Символдар мен жиындардың белгіленулерін пайдаланып, қос теңсіздіктің шешімдер жиынын жазамыз. Оны былайша оқиды: «х екіден артық және сегізден кем». Оның шешімін барлық шешімдердің жиыны түрінде жазуға болады, оны С жиыны деп жазайық. Жауабы: 2 < х < 8 қос теңсіздігінің шешімдер жиыны С = {3, 4, 5, 6, 7}

5 слайд

6 слайд
Мысалдар талдау. А) Қос теңсіздік жаз және оқы деген тапсырма төмендегідей үлгіде орындалады. 1) х белгісіз 5-тен артық және 9-дан кем; 5 < х < 9; 2) b белгісіз 27-ден артық және 32-ден кем; 27 < b < 32; 3) у белгісіз 14-тен артық және 19-дан кем; 14 < у < 19; 4) а белгісіз 40-тан артық және 45-тен кем. 40 < а < 45; Ә)Екі теңсіздіктен қос теңсіздік құр деген тапсырма төмендегідей үлгіде орындалады: 3 < х және х < 9; 3 < х < 9; 6 < у және у < 11; 6 < у < 11; 7 < с және с < 15; 7 < с < 15 opiq.kz электронды оқулық көмегімен тапсырмаларды орындап, жұмыстарыңызды тексеріп, қатемен жұмыс жасай аласың. Opiq.kz электронды оқулықтан өз қалауынша тапсырмалар орындау ұсынылады.

6 слайд

7 слайд
Тапсырмаларды дәптерге орында. Оқулықтан №2тапсырма, 5-ші бет. Теңсіздіктер шешімдер жиынын жаз және оны сан сәулесінде белгіле. (Үлгі түсіндірме жұмысында берілген) Оқулықтан №4тапсырма, 7-ші бет. Қос теңсіздіктер жаз. (Үлгі мысалдар талдауында берілген) Оқулықтан №5тапсырма,7-ші бет. Қос теңсіздікті жеке екі теңсіздікке ауыстыр. Оқулықпен жұмыс

7 слайд

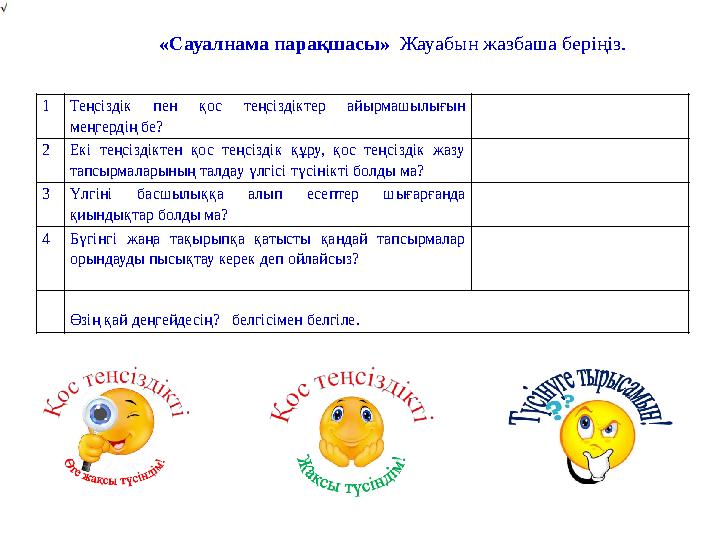
8 слайд
«Сауалнама парақшасы» Жауабын жазбаша беріңіз. 1 Теңсіздік пен қос теңсіздіктер айырмашылығын меңгердің бе? 2 Екі теңсіздіктен қос теңсіздік құру, қос теңсіздік жазу тапсырмаларының талдау үлгісі түсінікті болды ма? 3 Үлгіні басшылыққа алып есептер шығарғанда қиындықтар болды ма? 4 Бүгінгі жаңа тақырыпқа қатысты қандай тапсырмалар орындауды пысықтау керек деп ойлайсыз? Өзің қай деңгейдесің? белгісімен белгіле.

8 слайд

9 слайд
Тапсырмаларды дәптерге орында. № 1 есеп. 5-бет № 7 есеп. 7-бет № 11 есеп. 8-бет

9 слайд