Материалдар / Ашық сабақ 11 сынып Логорифмдік теңдеулер мен теңсіздіктер

Ашық сабақ 11 сынып Логорифмдік теңдеулер мен теңсіздіктер

Материал туралы қысқаша түсінік

Математика пәніне арналған сабақ

Аяпбергенова Айгуль Мухитовна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

12 Мамыр 2020

625

0 рет жүктелген

Математика Презентация 11 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 19

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Логарифмдік теңдеулерді шешу

1 слайд

Логарифмдік теңдеулерді шешу

2 слайд
Сабақтың мақсаты: 1. Оқушыларға логарифмдік теңдеулерді шешудің әдістерін оқытып-үйрету. 2. Логарифмдік теңдеулерді шешу үшін алдымен берілген логарифмдік функцияның анықталу облысын табу керектігін, логарифмнің анықтамасын және логарифмнің қасиеттерін қолдана алу дағдыларын арттыру, есептерді өз бетінше шығара алуы іскерліктерін арттыру. 3. Оқушыларды еңбек сүйгіштікке, адалдыққа, тиянақтылыққа, зейінділікке тәрбиелеу.

2 слайд

Сабақтың мақсаты: 1. Оқушыларға логарифмдік теңдеулерді шешудің әдістерін оқытып-үйрету. 2. Логарифмдік теңдеулерді шешу үшін алдымен берілген логарифмдік функцияның анықталу облысын табу керектігін, логарифмнің анықтамасын және логарифмнің қасиеттерін қолдана алу дағдыларын арттыру, есептерді өз бетінше шығара алуы іскерліктерін арттыру. 3. Оқушыларды еңбек сүйгіштікке, адалдыққа, тиянақтылыққа, зейінділікке тәрбиелеу.

3 слайд

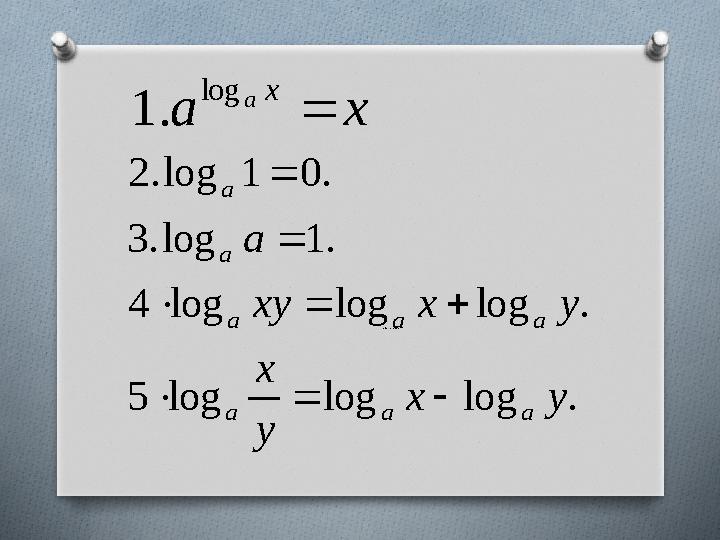
4 слайд
 0,0aаа х a x a  log . 1 . log log log 5 . log log log 4 . 1 log . 3 . 0 1 log . 2 y x y x y x xy a a a a a a a a a        

4 слайд

 0,0aаа х a x a  log . 1 . log log log 5 . log log log 4 . 1 log . 3 . 0 1 log . 2 y x y x y x xy a a a a a a a a a        

5 слайд
Анықтама : Айнымалысы логарифм таңбасының астында орналасқан теңдеу логарифмдік теңдеу деп аталады Қарапайым логарифмдік теңдеу log a х = б (а > 0, а≠ 1, б>0 ) Теңдеу шешу тәсілдері: 1. Логарифмнің анықтамасын қолдану арқылы шешу log a х = б (а > 0, а≠ 1, б>0 ) теңдеу түбірі х = а b түрінде беріледі 2. Потенциялдау әдісі. Потенциялдау ұғымын логарифмі бар теңдеулерді логарифмсіз теңдеуге келтіру деп түсінуге болады. Мысалы, егер log a f(х) = log a g(х) берілсе f(х) = g(х), f(х)>0, g(х)>0 , а > 0, а≠ 1. 3. Жаңа айнымалы енгізу тәсілі 4. Теңдіктің екі жағын логарифмдеу 5. Логарифмдерді бір негізге келтіру 6. Функционалды-графикалық әдіс

5 слайд

Анықтама : Айнымалысы логарифм таңбасының астында орналасқан теңдеу логарифмдік теңдеу деп аталады Қарапайым логарифмдік теңдеу log a х = б (а > 0, а≠ 1, б>0 ) Теңдеу шешу тәсілдері: 1. Логарифмнің анықтамасын қолдану арқылы шешу log a х = б (а > 0, а≠ 1, б>0 ) теңдеу түбірі х = а b түрінде беріледі 2. Потенциялдау әдісі. Потенциялдау ұғымын логарифмі бар теңдеулерді логарифмсіз теңдеуге келтіру деп түсінуге болады. Мысалы, егер log a f(х) = log a g(х) берілсе f(х) = g(х), f(х)>0, g(х)>0 , а > 0, а≠ 1. 3. Жаңа айнымалы енгізу тәсілі 4. Теңдіктің екі жағын логарифмдеу 5. Логарифмдерді бір негізге келтіру 6. Функционалды-графикалық әдіс

6 слайд
І Логарифмнің анықтамасын қолдану арқылы шығарылатын теңдеулер . 2 Потенциалдауды қолдану үшін логарифмдік теңдеуді түріне келтіру . 3 Жаңа айнымалы енгізу тәсілі. 4 Мүшелеп логарифмдеу тәсілі

6 слайд

І Логарифмнің анықтамасын қолдану арқылы шығарылатын теңдеулер . 2 Потенциалдауды қолдану үшін логарифмдік теңдеуді түріне келтіру . 3 Жаңа айнымалы енгізу тәсілі. 4 Мүшелеп логарифмдеу тәсілі

7 слайд
2-бөлім, Білімді пайдалану (ауызша) Мәнін тап: Log 2 16 = Log 5 1 = Log 5 25 = Log 3 81 = Log 0,2 0,04 =

7 слайд

2-бөлім, Білімді пайдалану (ауызша) Мәнін тап: Log 2 16 = Log 5 1 = Log 5 25 = Log 3 81 = Log 0,2 0,04 =

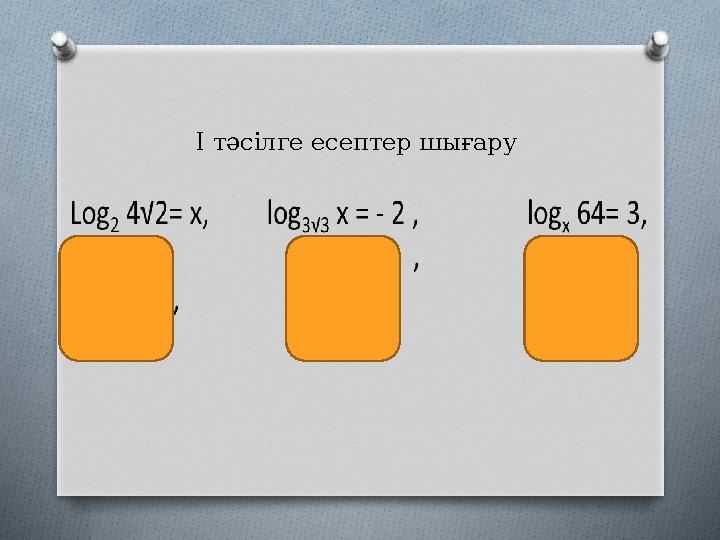
8 слайд
І тәсілге есептер шығару

8 слайд

І тәсілге есептер шығару

9 слайд
Потенциалдауды қолдану арқылы есеп шығару0 ) 25 lg( ) 5 lg( 2     x x Анықталу облысын табамыз:        0 25 , 0 5 2 x x немесе ) ;5( 0 ) 5 )( 5 ( , 0 5           х x x ) 25 lg( ) 5 lg( 2    x x 25 5 2    x x 0 30 2    х x . 5 , 6 2 1    х x ) ;5( 6   ) ;5( 5    Жауабы:6

9 слайд

Потенциалдауды қолдану арқылы есеп шығару0 ) 25 lg( ) 5 lg( 2     x x Анықталу облысын табамыз:        0 25 , 0 5 2 x x немесе ) ;5( 0 ) 5 )( 5 ( , 0 5           х x x ) 25 lg( ) 5 lg( 2    x x 25 5 2    x x 0 30 2    х x . 5 , 6 2 1    х x ) ;5( 6   ) ;5( 5    Жауабы:6

10 слайд
3-тәсіл Жаңа айнымалы енгізу тәсілі

10 слайд

3-тәсіл Жаңа айнымалы енгізу тәсілі

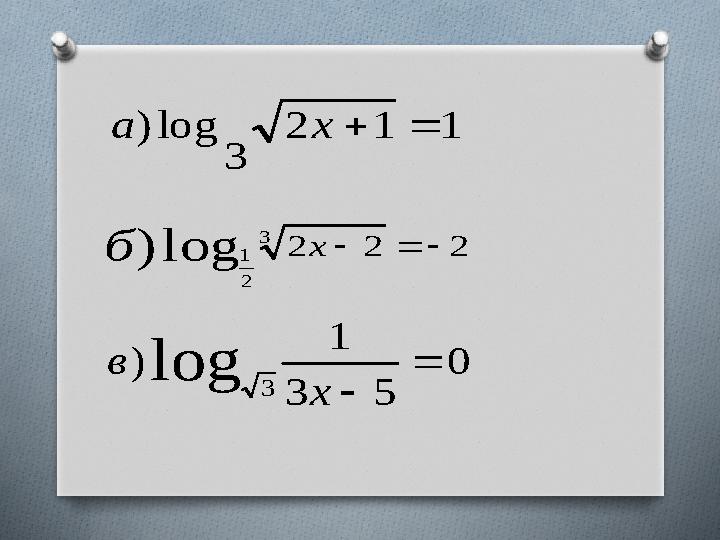
11 слайд
1 1 2 3 log )   x а 2 2 2 3 2 1 log )    x б 0 5 3 1 ) log 3   x в

11 слайд

1 1 2 3 log )   x а 2 2 2 3 2 1 log )    x б 0 5 3 1 ) log 3   x в

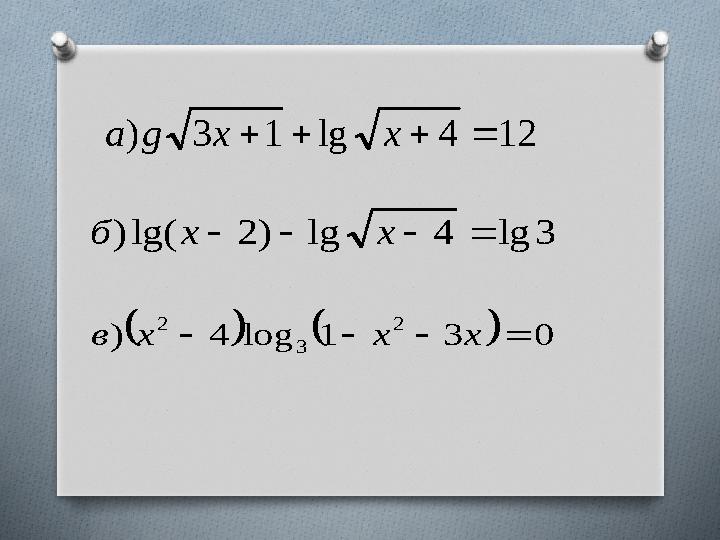
12 слайд
12 4 lg 1 3 )     x x g а 3 lg 4 lg ) 2 lg( )     x x б     0 3 1 log 4 ) 2 3 2     x x x в

12 слайд

12 4 lg 1 3 )     x x g а 3 lg 4 lg ) 2 lg( )     x x б     0 3 1 log 4 ) 2 3 2     x x x в

13 слайд
1-н ұсқаp a x log. 1 Негізі қандай? а)х ә)р б)а в) негізі жоқ 2 log. 2 5   x а) 25 ә)1/25 б)-25 в)- 1/25 3. log 7 (4 -x)=1 а) 7 ә) 4 б) 1 в)- 3 4. log 5 (x+1)= log 5 (4x-5) а) - 2 ә) 1/2 б)-2 в)-1/2 1 1 2 log. 5 3   x а) -4 ә) 4 б) 5 в) -5 2 -н ұсқа B x a  log. 1 Логарифмдік теңдеуінің қандай жағдайда бір ғана түбірі болады?  0 ,0   a а а  1 ,0   a а б  1 ,0   a а б  1 ,0   a а б Теңдеуді шешіңдер? 2 lg. 2  x а)1000 ә)100 б)10 в)- 100   2 1 2 log. 3 3   x а)3 ә)2 б)1 в)5     x х 2 1 log 4 log. 4 2 2    а)-3 ә)3 б)1/3 в)-1/3 1 1 2 log. 5 3   х а)-5 ә)5 б)-4 в)4

13 слайд

1-н ұсқаp a x log. 1 Негізі қандай? а)х ә)р б)а в) негізі жоқ 2 log. 2 5   x а) 25 ә)1/25 б)-25 в)- 1/25 3. log 7 (4 -x)=1 а) 7 ә) 4 б) 1 в)- 3 4. log 5 (x+1)= log 5 (4x-5) а) - 2 ә) 1/2 б)-2 в)-1/2 1 1 2 log. 5 3   x а) -4 ә) 4 б) 5 в) -5 2 -н ұсқа B x a  log. 1 Логарифмдік теңдеуінің қандай жағдайда бір ғана түбірі болады?  0 ,0   a а а  1 ,0   a а б  1 ,0   a а б  1 ,0   a а б Теңдеуді шешіңдер? 2 lg. 2  x а)1000 ә)100 б)10 в)- 100   2 1 2 log. 3 3   x а)3 ә)2 б)1 в)5     x х 2 1 log 4 log. 4 2 2    а)-3 ә)3 б)1/3 в)-1/3 1 1 2 log. 5 3   х а)-5 ә)5 б)-4 в)4

14 слайд
I. а ә б в 1 + 2 + 3 + 4 + 5 + ІІ. а ә б в 1 + 2 + 3 + 4 + 5 +

14 слайд

I. а ә б в 1 + 2 + 3 + 4 + 5 + ІІ. а ә б в 1 + 2 + 3 + 4 + 5 +

15 слайд
          20 5 5 30 5 5 ) у х у х а           1 12 2 2 ) у х у х б           2 32 * 2 ) у х у х в

15 слайд

          20 5 5 30 5 5 ) у х у х а           1 12 2 2 ) у х у х б           2 32 * 2 ) у х у х в

16 слайд
Бағалау Үйге тапсырма: Кітаппен жұмыс

16 слайд

Бағалау Үйге тапсырма: Кітаппен жұмыс

17 слайд
Мына қызықты қараңыз? “ 2 > 3” 1/4 > 1/8 бұл даусыз ақиқат (1/2) 2 > (1/2) 3 , бұл да күмән келтірмейді. Үлкен санға үлкен логарифм сәйкес келеді: lg(1/2) 2 > lg(1/2) 3 ; 2lg(1/2) > 3lg(1/2). lg(1/2) –ге қысқартудан кейін: 2 > 3. - Қай жерде қателік?

17 слайд

Мына қызықты қараңыз? “ 2 > 3” 1/4 > 1/8 бұл даусыз ақиқат (1/2) 2 > (1/2) 3 , бұл да күмән келтірмейді. Үлкен санға үлкен логарифм сәйкес келеді: lg(1/2) 2 > lg(1/2) 3 ; 2lg(1/2) > 3lg(1/2). lg(1/2) –ге қысқартудан кейін: 2 > 3. - Қай жерде қателік?

18 слайд
№ 1 -1; 0; 1; 2; 4; 8 сандарының қайсысы log 2 х=х-2 теңдеуінің түбірі болады? № 2 Теңдеулерін шеш: а) log 16 х= 2; в) log 2 (2х- х 2 ) -=0; г) log 3 (х-1)=log 3 (2х+1) № 3 у = log 2 (х+4) функциясының анықталу облысын тап № 4 Сандарды салыстыр: log 3 6/5 и log 3 5/6; log 0,2 5 и . L og 0,2 17. Қорытынды бөлім

18 слайд

№ 1 -1; 0; 1; 2; 4; 8 сандарының қайсысы log 2 х=х-2 теңдеуінің түбірі болады? № 2 Теңдеулерін шеш: а) log 16 х= 2; в) log 2 (2х- х 2 ) -=0; г) log 3 (х-1)=log 3 (2х+1) № 3 у = log 2 (х+4) функциясының анықталу облысын тап № 4 Сандарды салыстыр: log 3 6/5 и log 3 5/6; log 0,2 5 и . L og 0,2 17. Қорытынды бөлім