Ашық сабақ Алгебра 9 сынып 3 тоқсан

#1 слайд

1 слайд

#2 слайд
Оқушыларға сүйір бұрыштың тригонометриялық функциясының әрбір бұрышындағы синустыың, косинустың, тангенстің, котангенстің келтіру формулаларымен таныстыру, осы формулаларды тригонометриялық өрнектерді түрлендіруде және есептерді шығару кезінде қолдануды үйрету;

2 слайд

#3 слайд
Есте са қта!!! - Егер келтірілген тригонометриялық функцияның аргументі (бұрышы) π ± α (180 ± α ), 2 π ± α (360 ± α ) түрінде болса, онда оның аты өзгермейді. - Егер келтірілген тригонометриялық функцияның аргументі (бұрышы) π /2 ± α (90 ± α ), 3 π /2 ± α (270 ± α ) түрінде болса, онда синус косинусқа, косинус синусқа, тангенс котангенске, котангенс тангенске өзгереді; - Келтіру формуласының оң жағының таңбасы сәйкес ширектегі келтірілген функцияның таңбасымен бірдей жазылады.

3 слайд

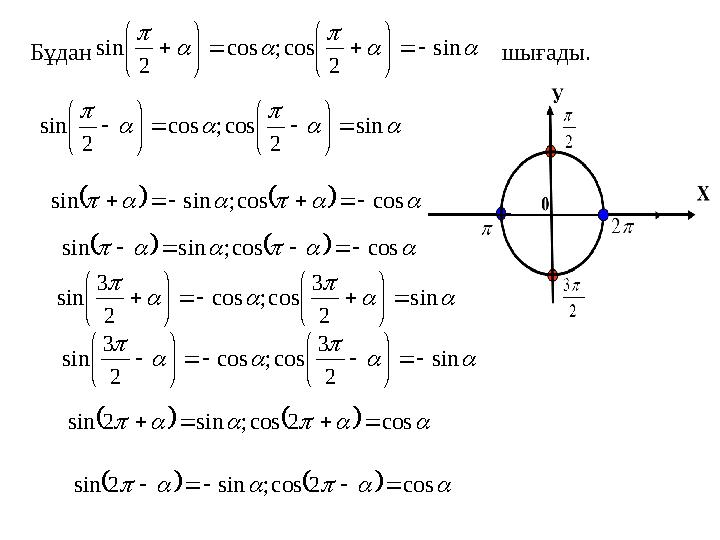
#4 слайд
      sin 2 cos; cos 2 sin                 Бұдан шығады.       sin 2 cos; cos 2 sin                           cos cos; sin sin                 cos cos; sin sin            sin 2 3 cos; cos 2 3 sin                        sin 2 3 cos; cos 2 3 sin                             cos 2 cos; sin 2 sin               cos 2 cos; sin 2 sin     

4 слайд

#5 слайд
Жоғарыдағы формулаларды пайдаланып, tg α ,ctg α - н ің келтіру формуласын шығаруға болады.      tg ctg ctg tg                   2 ; 2           сtg ctg tg tg       ;       tg ctg ctg tg                   2 3 ; 2 3           сtg ctg tg tg       2 ; 2

5 слайд

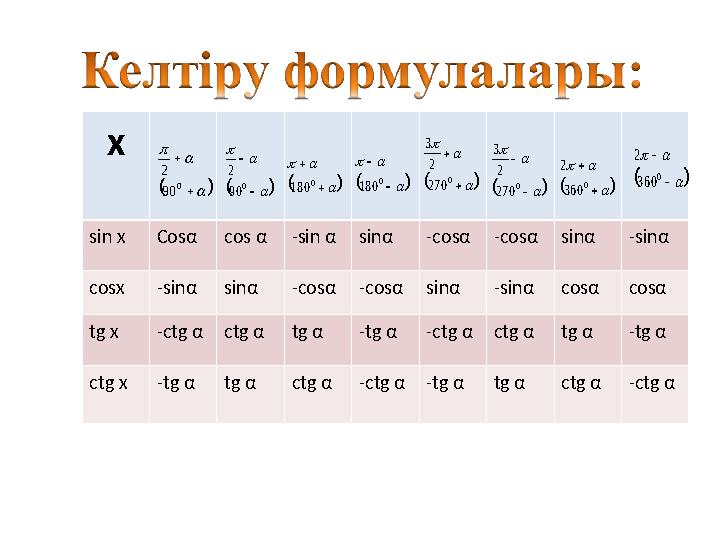
#6 слайд
х sin x Cos α cos α -sin α sin α -cos α -cos α sin α -sin α cosx -sin α sin α -cos α -cos α sin α -sin α cos α cos α tg x -ctg α ctg α tg α -tg α -ctg α ctg α tg α -tg α ctg x -tg α tg α ctg α -ctg α -tg α tg α ctg α -ctg α       0 90 2        0 90 2        0 180        0 180        0 270 2 3        0 270 2 3        0 360 2        0 360 2

6 слайд

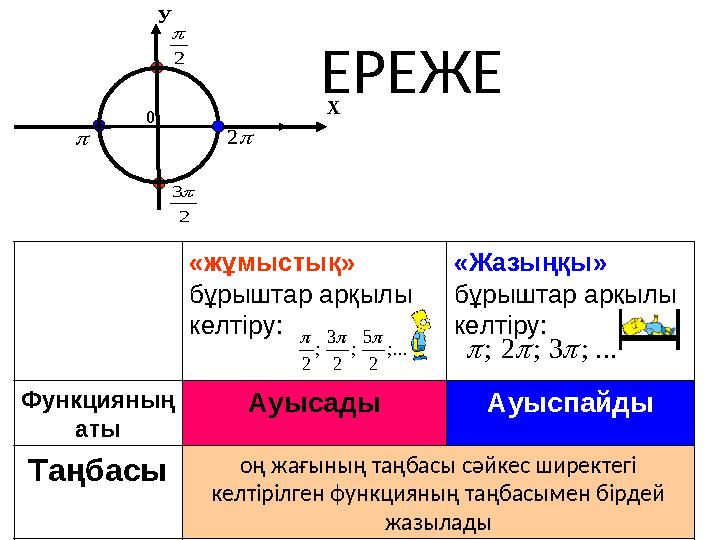
#7 слайд
ЕРЕЖЕ «жұмыстық» бұрыштар арқылы келтіру: «Жазыңқы» бұрыштар арқылы келтіру: Функцияның аты Ауысады Ауыспайды Таңбасы оң жағының таңбасы сәйкес ширектегі келтірілген функцияның таңбасымен бірдей жазылады...; 2 5 ; 2 3 ; 2    ... ; 3 ; 2 ;    2 0 У 2 3   2 Х

7 слайд

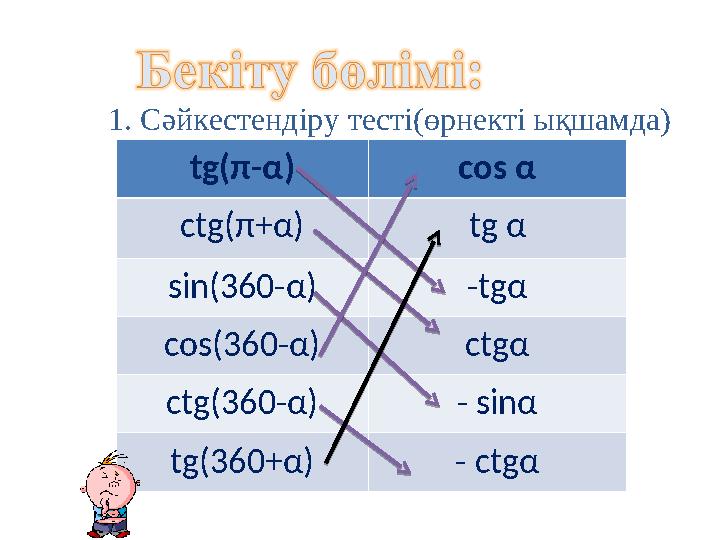
#8 слайд
1. Сәйкестендіру тесті(өрнекті ықшамда) tg( π - α ) cos α ctg( π + α ) tg α sin(360- α ) - tg α cos(360- α ) ctg α ctg(360- α ) - sin α tg(360+ α ) - ctg α

8 слайд

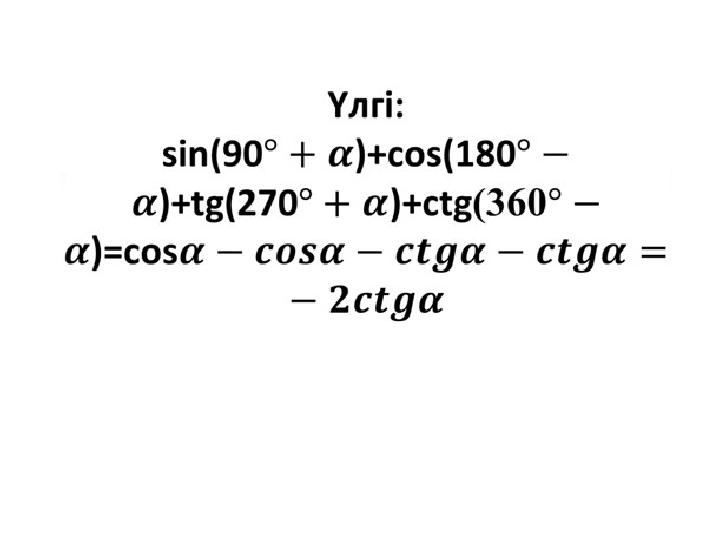
#9 слайд

9 слайд

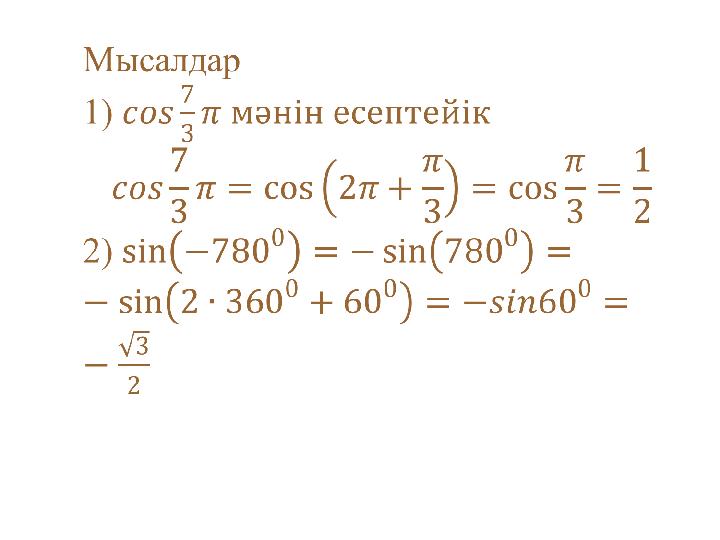
#10 слайд

10 слайд

#11 слайд

11 слайд

#12 слайд
1. 2 .         0 0 90 180 ctg tg          0 0 2 360 cos 1 180 sin                                                                                                     2 sin 2 cos 2 2 3 . 4 90 360 360 sin 270 sin. 3 2 3 cos 2 sin. 2 360 270 180 cos 90 sin. 1 2 2 0 3 0 3 0 2 0 2 0 0 0 0 tg tg tg ctg ctg tg ctg tg

12 слайд

#13 слайд
1. 2 . 1   cos  1 . 4 1. 3 cos 2. 2 2 . 1     ctg         0 0 0 0 0 0 0 0 0 0 0 0 15 15 90 15 15 90 15 sin 15 90 cos 15 cos 15 90 sin) tg ctg ctg tg а                 0 0 0 0 0 0 0 0 0 0 0 0 15 30 180 15 30 180 15 cos 30 180 cos 15 sin 30 180 sin) ctg ctg tg tg а                    0 0 0 0 0 0 0 0 0 0 0 0 20 20 180 20 20 180 20 cos 20 180 cos 20 sin 20 180 sin) ctg ctg tg tg а          

13 слайд

#14 слайд

14 слайд

#15 слайд

15 слайд