Ашық сабақ. Келтіру формулалары

#1 слайд

1 слайд

#2 слайд
Біліктілік: Оқушыларға сүйір бұрыштың тригонометриялық функциясының әрбір бұрышындағы синустыың, косинустың, тангенстің, котангенстің келтіру формулаларымен таныстыру, осы формулаларды тригонометриялық өрнектерді түрлендіруде және есептерді шығару кезінде қолдануды үйрету; Дамытушылық: Оқушылардың ақыл-ойын дамыту, ойлау қабілетін жетілдіру. Тәрбиелік: Оқушылардың алгебра пәніне қызығушылығын арттыру, оқушыларды алғырлыққа, шапшандыққа тәрбиелеу.

2 слайд

#3 слайд
І. Ұйымдастыру. ІІ. Үй тапсырмасын тексеру ІІІ. Жаңа сабақ. “Ой қозғау” ІҮ. Бекіту бөлімі. 1.Сәйкестендіру тесті 2.“Математикалық жәрмеңке” деңгейлік тапсырмалар Ү. Бағалау

3 слайд

#4 слайд
Егер бұрышының функциялары берілсе, онда оларды α бұрышына байланысты тригонометриялық функцияларға келтіру ыңғайлы.   k 2 Келтіру формулаларын k =1;2;3;4 болған жағдайда, өрнегін, яғни бұрыштары үшін қарастырамыз.   k 2      2; 2 3 ;; 2

4 слайд

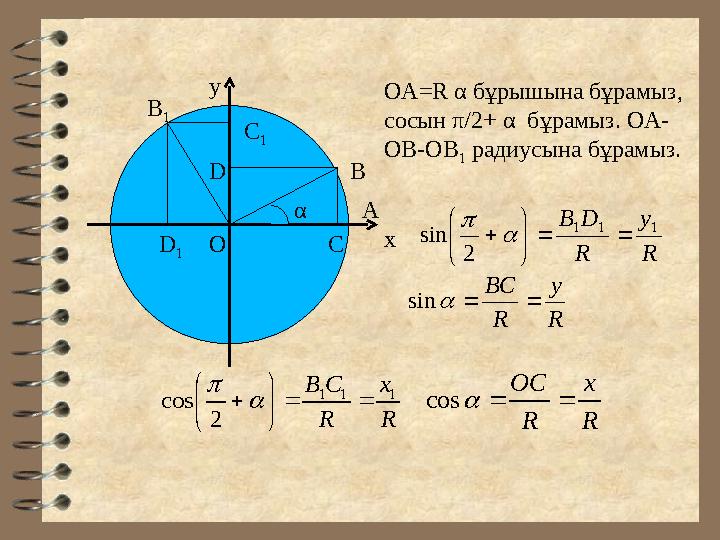
#5 слайд
х у В 1 D 1 C 1 D B C α O A ОА=R α бұрышына бұрамыз, сосын π/2+ α бұрамыз. ОА- ОВ-ОВ 1 радиусына бұрамыз. R y R DB 111 2 sin         R y R BC sin R x R СB 111 2 cos         R x R OC cos

5 слайд

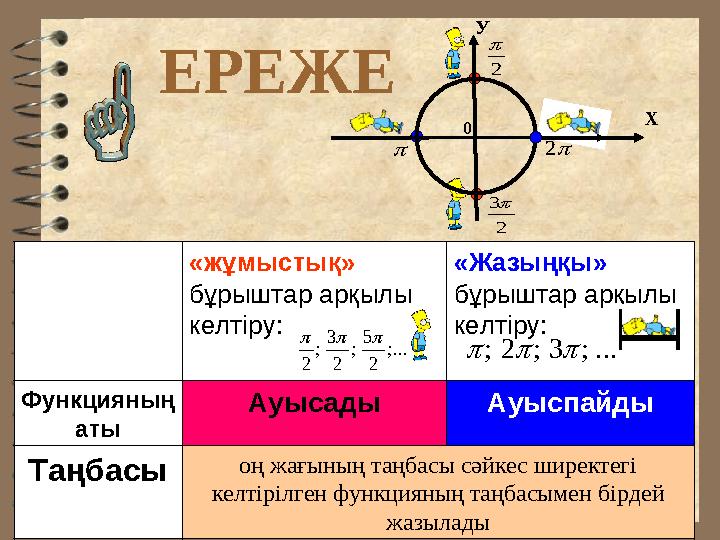
#6 слайд
ЕРЕЖЕ «жұмыстық» бұрыштар арқылы келтіру: «Жазыңқы» бұрыштар арқылы келтіру: Функцияның аты Ауысады Ауыспайды Таңбасы оң жағының таңбасы сәйкес ширектегі келтірілген функцияның таңбасымен бірдей жазылады ...; 2 5 ; 2 3 ; 2  ...;3;2; 2  0 У 2 3  2 Х

6 слайд

#7 слайд
    sin 2 cos;cos 2 sin             Бұдан шығады.     sin 2 cos;cos 2 sin                 coscos;sinsin     coscos;sinsin      sin 2 3 cos;cos 2 3 sin                  sin 2 3 cos;cos 2 3 sin                  cos2cos;sin2sin      cos2cos;sin2sin 

7 слайд

#8 слайд
Жоғарыдағы формулаларды пайдаланып, tgα,ctgα-нің келтіру формуласын шығаруға болады.     tgctgctgtg               2 ; 2   сtgctgtgtg  ;     tgctgctgtg               2 3 ; 2 3     сtgctgtgtg  2;2

8 слайд

#9 слайд
Есте сақта!!! -Егер келтірілген тригонометриялық функцияның аргументі (бұрышы) π ±α (180 ±α), 2π ±α (360 ±α) түрінде болса, онда оның аты өзгермейді. -Егер келтірілген тригонометриялық функцияның аргументі (бұрышы) π/2 ±α (90 ±α), 3π/2 ±α (270 ±α) түрінде болса, онда синус косинусқа, косинус синусқа, тангенс котангенске, котангенс тангенске өзгереді; -Келтіру формуласының оң жағының таңбасы сәйкес ширектегі келтірілген функцияныі таңбасымен бірдей жазылады.

9 слайд

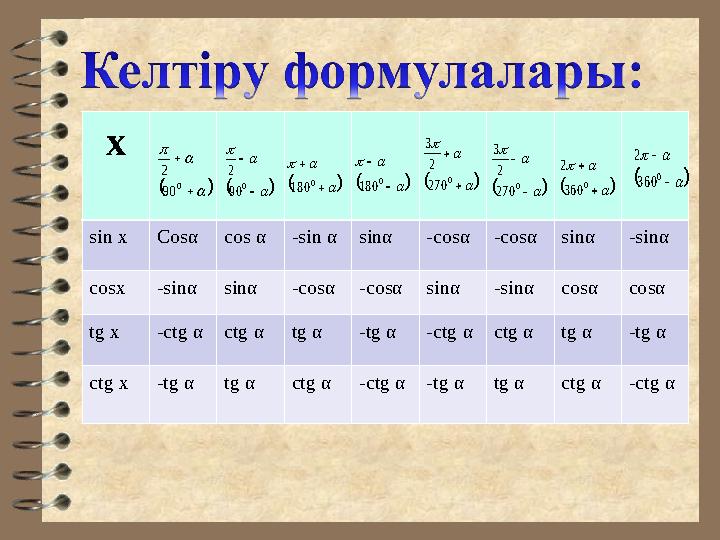
#10 слайд
х sin xCosαcos α-sin αsinα-cosα-cosαsinα-sinα cosx-sinαsinα-cosα-cosαsinα-sinαcosαcosα tg x-ctg αctg αtg α-tg α-ctg αctg αtg α-tg α ctg x-tg αtg αctg α-ctg α-tg αtg αctg α-ctg α       0 90 2       0 90 2      0 180      0 180       0 270 2 3       0 270 2 3      0 360 2      0 360 2

10 слайд

#11 слайд

11 слайд

#12 слайд
1. Сәйкестендіру тесті(өрнекті ықшамда) tg(π-α) cos α ctg(π+α) tg α sin(360-α) -tgα cos(360-α) ctgα ctg(360-α) - sinα tg(360+α) - ctgα

12 слайд

#13 слайд
Оқулықпен жұмыс №334

13 слайд

#14 слайд

14 слайд

#15 слайд
1. 2.        0 0 90 180 ctg tg        0 02 360cos 1180sin а)75 ә) 150 б)200 бұрыштарының барлық тригонометриялық функциясын аргументі 45- тан аспайтын функциямен ауыстырыңдар.                                                       2sin 2 cos2 2 3 .4 90360360sin270sin.3 2 3 cos 2 sin.2 360270180cos90sin.1 22 03030202 0000 tgtg tgctg ctgtg ctgtg

15 слайд

#16 слайд
1. 2. 1 cos 1.4 1.3 cos2.2 2.1    ctg         000 000 000 000 151590 151590 15sin1590cos 15cos1590sin) tgctg ctgtg а             000 000 000 000 1530180 1530180 15cos30180cos 15sin30180sin) ctgctg tgtg а             000 000 000 000 2020180 2020180 20cos20180cos 20sin20180sin) ctgctg tgtg а    

16 слайд

#17 слайд

17 слайд

#18 слайд

18 слайд

#19 слайд

19 слайд