Материалдар / Ашық сабақ Қосу формулалары 9-сынып

Ашық сабақ Қосу формулалары 9-сынып

Материал туралы қысқаша түсінік

презентацияны сабаққа қолдануға болады.

Сахова Акмарал Байдосовна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

08 Қаңтар 2019

1073

10 рет жүктелген

Алгебра Ашық сабақ 9 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 29

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
9 “а” сынып

1 слайд

9 “а” сынып

2 слайд
Сабақтың мақсаты: •І Білімділік: Тригонометриялық қосу формулаларын пайдалану, білік дағдыларын қалыптастыру, есептерді шешу кезінде тиімді пайдалана білуге үйрету. •ІІ. Тәрбиелік: Оқушыларды шыдамдылыққа, дәлдікке, шапшаңдыққа, ұқыптылыққа, ұжымдастыққа, достыққа тәрбиелеу. • ІІІ. Дамытушылық: Оқушылардың өз бетінше білім алу дағдыларын қалыптастыру, логикалық ойлау,шығармашылық қабілетін дамыту,пәнге қызығушылығын арттыру.

2 слайд

Сабақтың мақсаты: •І Білімділік: Тригонометриялық қосу формулаларын пайдалану, білік дағдыларын қалыптастыру, есептерді шешу кезінде тиімді пайдалана білуге үйрету. •ІІ. Тәрбиелік: Оқушыларды шыдамдылыққа, дәлдікке, шапшаңдыққа, ұқыптылыққа, ұжымдастыққа, достыққа тәрбиелеу. • ІІІ. Дамытушылық: Оқушылардың өз бетінше білім алу дағдыларын қалыптастыру, логикалық ойлау,шығармашылық қабілетін дамыту,пәнге қызығушылығын арттыру.

3 слайд
Сабақтың барысы: 1. Сабақты ұйымдастыру. 2. Үй тапсырмасын тексеру. №488 3. Жаңа сабаққа әзірлік бағытында өткен тақырыптардан (қайталау сұрақтары) а) Тригонометриялық функцияларды ата ә) Тригонометриялық функцияның қасиеттері б) 30, 45, 60, 90, 180 градустарды радианға келтір

3 слайд

Сабақтың барысы: 1. Сабақты ұйымдастыру. 2. Үй тапсырмасын тексеру. №488 3. Жаңа сабаққа әзірлік бағытында өткен тақырыптардан (қайталау сұрақтары) а) Тригонометриялық функцияларды ата ә) Тригонометриялық функцияның қасиеттері б) 30, 45, 60, 90, 180 градустарды радианға келтір

4 слайд
sin(α+β) =sinα·cosβ+cosα ·sinβ (1) sin(α-β) =sinα·cosβ-cosα · sinβ (2) cos(α+β) =cosα·cosβ-sinα·sinβ (3) cos(α-β) =cosα·cosβ+sinα·sinβ (4)

4 слайд

sin(α+β) =sinα·cosβ+cosα ·sinβ (1) sin(α-β) =sinα·cosβ-cosα · sinβ (2) cos(α+β) =cosα·cosβ-sinα·sinβ (3) cos(α-β) =cosα·cosβ+sinα·sinβ (4)

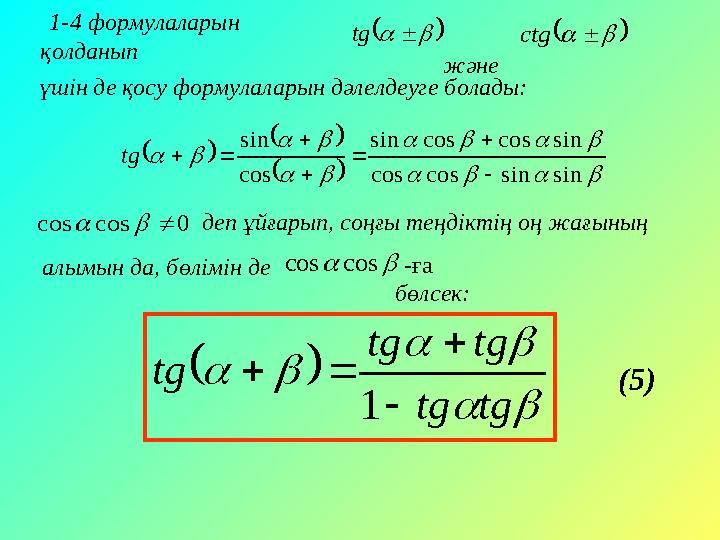
5 слайд
 tg  ctg            sinsincoscos sincoscossin cos sin      tg 0coscos  coscos      tgtg tgtg tg    1 1-4 формулаларын қолданып деп ұйғарып, соңғы теңдіктің оң жағының және үшін де қосу формулаларын дәлелдеуге болады: алымын да, бөлімін де (5) -ға бөлсек:

5 слайд

 tg  ctg            sinsincoscos sincoscossin cos sin      tg 0coscos  coscos      tgtg tgtg tg    1 1-4 формулаларын қолданып деп ұйғарып, соңғы теңдіктің оң жағының және үшін де қосу формулаларын дәлелдеуге болады: алымын да, бөлімін де (5) -ға бөлсек:

6 слайд
    tgtg tgtg tg    1      tgtg ctgtg ctg    1     tgtg ctgtg ctg    1 Осыған ұқсас түрлендірулерді қолдансақ:Осыған ұқсас түрлендірулерді қолдансақ: (6) (8 ) (7) формулаларын формулаларын аламыз.аламыз.

6 слайд

    tgtg tgtg tg    1      tgtg ctgtg ctg    1     tgtg ctgtg ctg    1 Осыған ұқсас түрлендірулерді қолдансақ:Осыған ұқсас түрлендірулерді қолдансақ: (6) (8 ) (7) формулаларын формулаларын аламыз.аламыз.

7 слайд
1-мысал:1-мысал:    31 4 2 2 2 2 3 2 2 2 1 45sin30cos45cos30sin4530sin75sin 0000000  0 75sin  31 4 2 Жауабы:Жауабы:

7 слайд

1-мысал:1-мысал:    31 4 2 2 2 2 3 2 2 2 1 45sin30cos45cos30sin4530sin75sin 0000000  0 75sin  31 4 2 Жауабы:Жауабы:

8 слайд
2-мысал:2-мысал: sin 64 cos 26 + cos 64 sin 26   190sin2664sin 000 sin 64 cos 26 + cos 64 sin 26 0 0 0 0 Жауабы:Жауабы: 1

8 слайд

2-мысал:2-мысал: sin 64 cos 26 + cos 64 sin 26   190sin2664sin 000 sin 64 cos 26 + cos 64 sin 26 0 0 0 0 Жауабы:Жауабы: 1

9 слайд
Сергіту сәтіСергіту сәті

9 слайд

Сергіту сәтіСергіту сәті

10 слайд
Есептер шығару Өрнектi ықшамдаңыз: 8 sin 8 3 sin 8 cos 8 3 cos  1.

10 слайд

Есептер шығару Өрнектi ықшамдаңыз: 8 sin 8 3 sin 8 cos 8 3 cos  1.

11 слайд
2 2 4 cos 8 2 cos 8 3 cos 88 3 cos            8 sin 8 3 sin 8 cos 8 3 cos  Шешуі: Жауабы: Жауабы: 2 2

11 слайд

2 2 4 cos 8 2 cos 8 3 cos 88 3 cos            8 sin 8 3 sin 8 cos 8 3 cos  Шешуі: Жауабы: Жауабы: 2 2

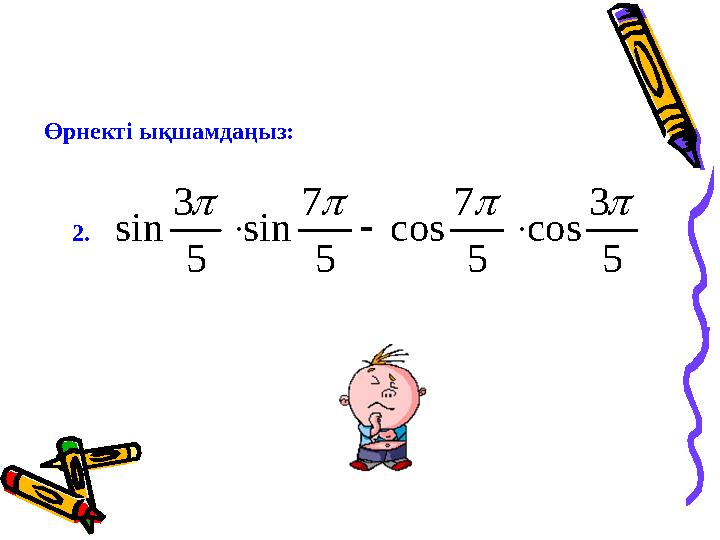
12 слайд
5 3 cos 5 7 cos 5 7 sin 5 3 sin  2. Өрнектi ықшамдаңыз:

12 слайд

5 3 cos 5 7 cos 5 7 sin 5 3 sin  2. Өрнектi ықшамдаңыз:

13 слайд
Шешуі:  5 3 cos 5 7 cos 5 7 sin 5 3 sin  12cos 5 10 cos 5 37 cos 5 3 5 7 cos            Жауабы: Жауабы: 1

13 слайд

Шешуі:  5 3 cos 5 7 cos 5 7 sin 5 3 sin  12cos 5 10 cos 5 37 cos 5 3 5 7 cos            Жауабы: Жауабы: 1

14 слайд
3. Өрнектi ықшамдаңыз: tg tg tgtg 22 23 1 2223      

14 слайд

3. Өрнектi ықшамдаңыз: tg tg tgtg 22 23 1 2223      

15 слайд
Шешуі: Жауабы: Жауабы: 1   1452322 23221 2322 000    tgtg tgtg tgtg  

15 слайд

Шешуі: Жауабы: Жауабы: 1   1452322 23221 2322 000    tgtg tgtg tgtg  

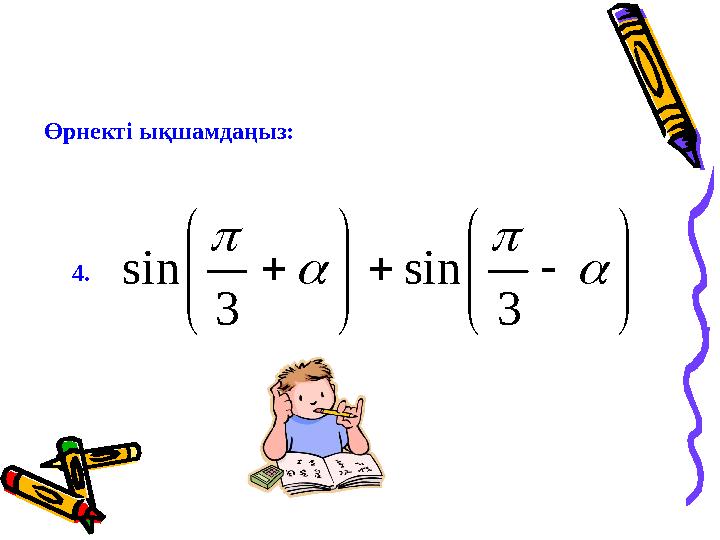
16 слайд
4. Өрнектi ықшамдаңыз:                  3 sin 3 sin

16 слайд

4. Өрнектi ықшамдаңыз:                  3 sin 3 sin

17 слайд
Шешуі: Жауабы: Жауабы:          sin 3 coscos 3 sinsin 3 coscos 3 sin                  3 sin 3 sin   cos3cos 2 3 2cos 3 sin2  cos3

17 слайд

Шешуі: Жауабы: Жауабы:          sin 3 coscos 3 sinsin 3 coscos 3 sin                  3 sin 3 sin   cos3cos 2 3 2cos 3 sin2  cos3

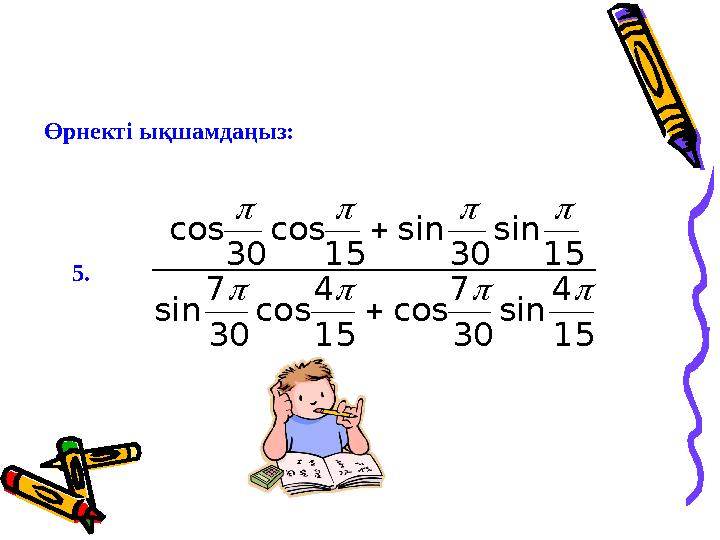
18 слайд
5. Өрнектi ықшамдаңыз: coscos sinsin sincos cossin     3015 3015 7 30 4 15 7 30 4 15  

18 слайд

5. Өрнектi ықшамдаңыз: coscos sinsin sincos cossin     3015 3015 7 30 4 15 7 30 4 15  

19 слайд
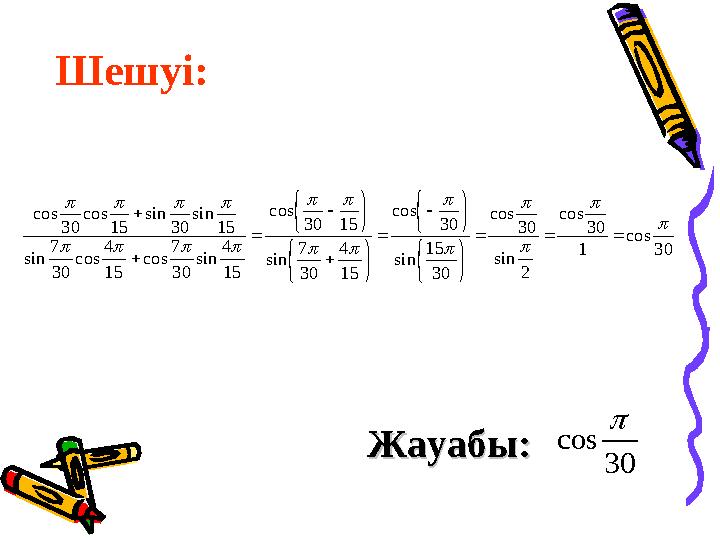
Шешуі: Жауабы: Жауабы: 30 cos 1 30 cos 2 sin 30 cos 30 15 sin 30 cos 15 4 30 7 sin 1530 cos 15 4 sin 30 7 cos 15 4 cos 30 7 sin 15 sin 30 sin 15 cos 30 cos                                           30 cos 

19 слайд

Шешуі: Жауабы: Жауабы: 30 cos 1 30 cos 2 sin 30 cos 30 15 sin 30 cos 15 4 30 7 sin 1530 cos 15 4 sin 30 7 cos 15 4 cos 30 7 sin 15 sin 30 sin 15 cos 30 cos                                           30 cos 

20 слайд
6. Өрнектi ықшамдаңыз: 3 tg15tg60 1tg15tg60 0 0 0 0    

20 слайд

6. Өрнектi ықшамдаңыз: 3 tg15tg60 1tg15tg60 0 0 0 0    

21 слайд
Шешуі: Жауабы: Жауабы:    21345345360153 tg60tg151 tg60tg15 3 0000 00 00     tgtgtg 2

21 слайд

Шешуі: Жауабы: Жауабы:    21345345360153 tg60tg151 tg60tg15 3 0000 00 00     tgtgtg 2

22 слайд
7. Өрнектi ықшамдаңыз: cos cos sin sin sin cos sin cos 20 65 20 65 75 30 30 75              

22 слайд

7. Өрнектi ықшамдаңыз: cos cos sin sin sin cos sin cos 20 65 20 65 75 30 30 75              

23 слайд
Шешуі: Жауабы: Жауабы: 1      145 45sin 45cos 45sin 45cos 3075sin 6520cos 75cos30sin30cos75sin 65sin20sin65cos20cos 0 0 0 0 0 00 00         ctg  

23 слайд

Шешуі: Жауабы: Жауабы: 1      145 45sin 45cos 45sin 45cos 3075sin 6520cos 75cos30sin30cos75sin 65sin20sin65cos20cos 0 0 0 0 0 00 00         ctg  

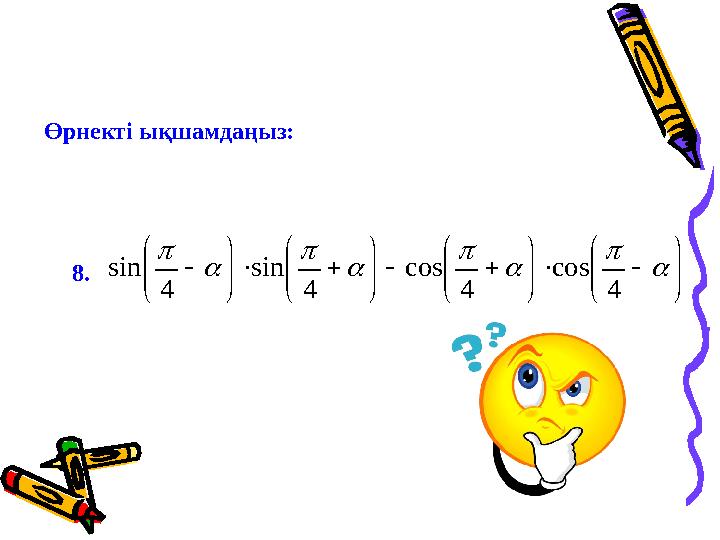
24 слайд
8. Өрнектi ықшамдаңыз:                                  4 cos 4 cos 4 sin 4 sin

24 слайд

8. Өрнектi ықшамдаңыз:                                  4 cos 4 cos 4 sin 4 sin

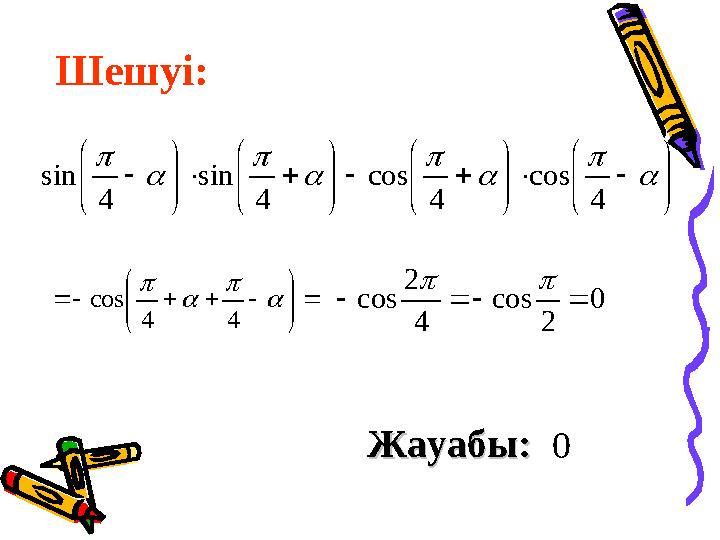
25 слайд
Шешуі: Жауабы: Жауабы:            44 cos                                  4 cos 4 cos 4 sin 4 sin 0 2 cos 4 2 cos   0

25 слайд

Шешуі: Жауабы: Жауабы:            44 cos                                  4 cos 4 cos 4 sin 4 sin 0 2 cos 4 2 cos   0

26 слайд
Сабақты қорытындылауСабақты қорытындылау   tgtg tgtg   1 tg   tgtg ctgtg  1 ctg   tgtg tgtg   1 tg   tgtg ctgtg  1 ctg 1 sin(α+β) А sinα·cosβ-cosα · sinβ 2 cos(α+β) Ә sinα·cosβ+cosα ·sinβ 3 cos(α-β) Б 4 В 5 Г 6 Ғ cosα·cosβ+sinα·sinβ 7 sin(α-β) Д 8 Е cosα·cosβ-sinα·sinβ

26 слайд

Сабақты қорытындылауСабақты қорытындылау   tgtg tgtg   1 tg   tgtg ctgtg  1 ctg   tgtg tgtg   1 tg   tgtg ctgtg  1 ctg 1 sin(α+β) А sinα·cosβ-cosα · sinβ 2 cos(α+β) Ә sinα·cosβ+cosα ·sinβ 3 cos(α-β) Б 4 В 5 Г 6 Ғ cosα·cosβ+sinα·sinβ 7 sin(α-β) Д 8 Е cosα·cosβ-sinα·sinβ

27 слайд
Үй тапсырмасы Үй тапсырмасы №№498-500 есептер498-500 есептер

27 слайд

Үй тапсырмасы Үй тапсырмасы №№498-500 есептер498-500 есептер

28 слайд
Сабақ аяқталды!Сабақ аяқталды!

28 слайд

Сабақ аяқталды!Сабақ аяқталды!