Ашық сабақ Тригонометриялық теңдеулерді шешу 10 сынып

1 слайд
Тригонометриялық Тригонометриялық теңдеулерді шешутеңдеулерді шешу 1010 сынып сынып АлгебраАлгебра

1 слайд

2 слайд
Сабақтың мақсаты: Тригонометриялық теңдеулерді шешуде қолданылатын формулалар мен әдістерді қайталау, жүйелеу. Тригонометриялық теңдеулерді шешу дағдысын жетілдіру.

2 слайд

3 слайд
Қайталау сұрақтары:Қайталау сұрақтары:

3 слайд

4 слайд
Тригонометриялық теңдеу дегеніміз не? Тригонометриялық функциялардың белгісіз аргументтері түрінде берілген теңдеулерді тригонометриялық теңдеулер деп атаймыз .

4 слайд

5 слайд
; sin a x  ; cos a x  ; a tgx  a ctgx 

5 слайд

6 слайд
Тригонометриялық теңдеулерді Тригонометриялық теңдеулерді шешу дегеніміз не?шешу дегеніміз не? Тригонометриялық теңдеулерді шешу дегеніміз – берілген теңдеуді тура теңдікке айналдыратын аргументтің барлық мәндерін табу .

6 слайд

7 слайд
Теңдеулер Шешімдері Ескертулерa x  sin   ) arcsin( a Z n n a x n     , arcsin )1 (  a x  cos a tgx  a ctgx   x  x  x a a arccos ) arccos(     1  a   ) ( a arctg   ) ( a arcctg R a  R a  1  a

7 слайд

8 слайд
2 3 cos  xфункциясының мәндері жиыны [-1;1] кесіндісі қарапайым теңдеу x y sin  Тригонометриялық теңдеулердің бір ғана шешімі болады. x y cos  функциясы – тақ функция 2 1 3 arccos   теңдеуінің шешімі Z n n a x     , arccos  болғанда теңдеудің шешімі болады. a x  cos болады a x  sin теңдеуі 1  a a a arccos ) arccos(     3 2 3 arcsin  1. 2. 4. 5. 6. 7. 8. 9. 10. , sin x y  функциялары-тақ функциялар x y arcsin  3. 2 3 cos  x функциясының мәндері жиыны [-1;1] кесіндісі қарапайым теңдеу x y sin  Тригонометриялық теңдеулердің бір ғана шешімі болады. x y cos  функциясы – тақ функция 2 1 3 arccos   теңдеуінің шешімі Z n n a x     , arccos  болғанда теңдеудің шешімі болады. a x  cos болады a x  sin теңдеуі 1  a a a arccos ) arccos(     3 2 3 arcsin  1. 2. 4. 5. 6. 7. 8. 9. 10. , sin x y  функциялары-тақ функциялар x y arcsin  3.

8 слайд

9 слайд
ІV. «Кім жылдам» ойыны. . ІV. «Кім жылдам» ойыны. . Сыныпты екі топқа бөлу . Синустар Сыныпты екі топқа бөлу . Синустар және косинустар тобыжәне косинустар тобы Ойын шарты: Ойын шарты: Кері Кері тригонометриялық тригонометриялық функциялардың мәндерін функциялардың мәндерін табуымыз керек табуымыз керек

9 слайд

10 слайд

10 слайд

11 слайд
Ауызша есептер

11 слайд

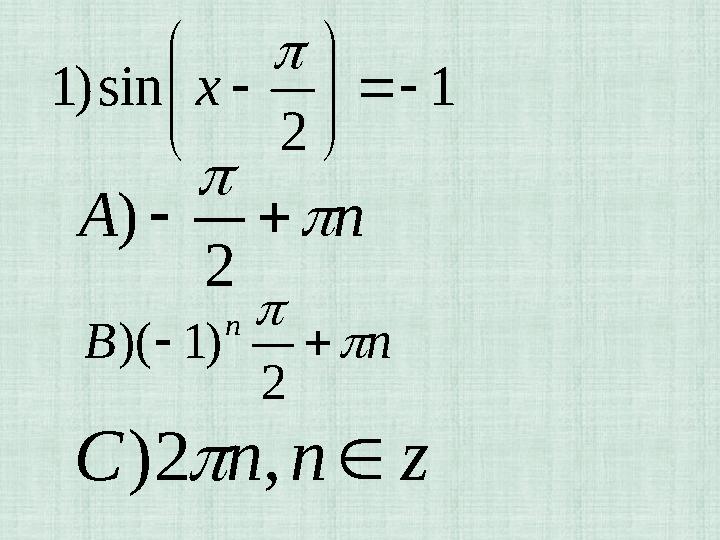
12 слайд
1 2 sin ) 1           x n A     2 ) n B n     2 ) 1 )( z n n C  , 2 ) 

12 слайд

13 слайд
Дұрыс!Дұрыс!z n n C  , 2 ) 

13 слайд

14 слайд
ДД ұұ рыс емес!рыс емес! Ойлан!Ойлан!

14 слайд

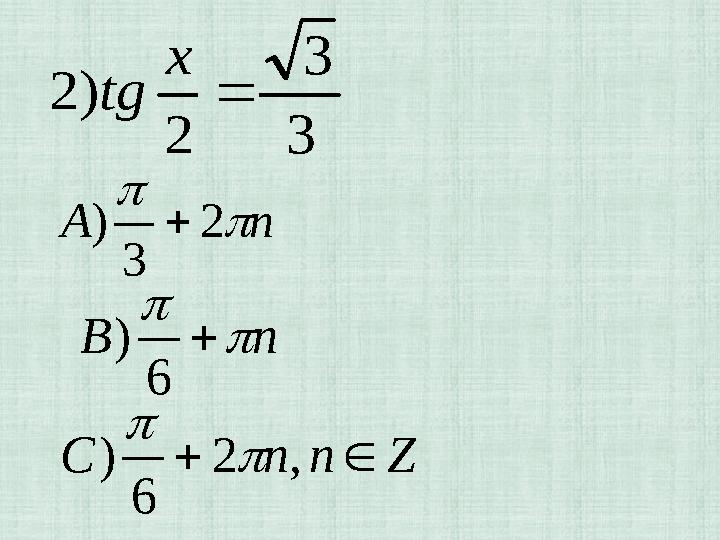
15 слайд
3 3 2 ) 2  x tg n А   2 3 )  n B    6 ) Z n n C   , 2 6 )  

15 слайд

16 слайд
Дұрыс!Дұрыс!n A   2 3 ) 

16 слайд

17 слайд
ДД ұұ рыс емес!рыс емес! Ойлан!Ойлан!

17 слайд

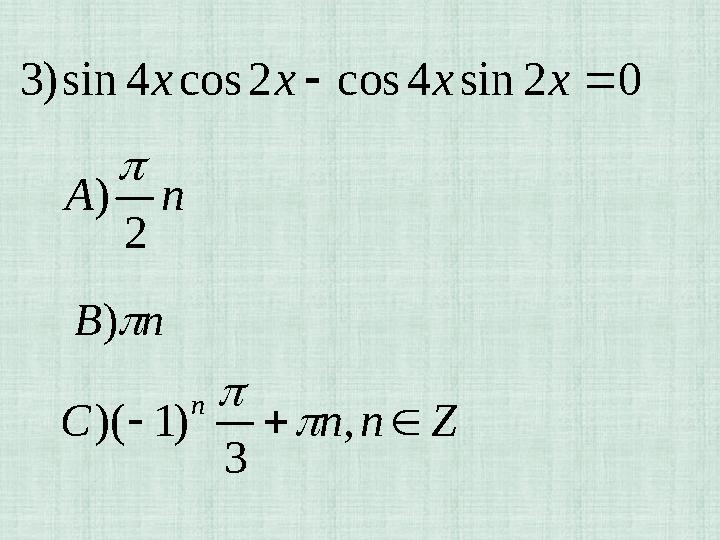
18 слайд
0 2 sin 4 cos 2 cos 4 sin ) 3   x x x x n А 2 )  n B  ) Z n n C n    , 3 ) 1 )(  

18 слайд

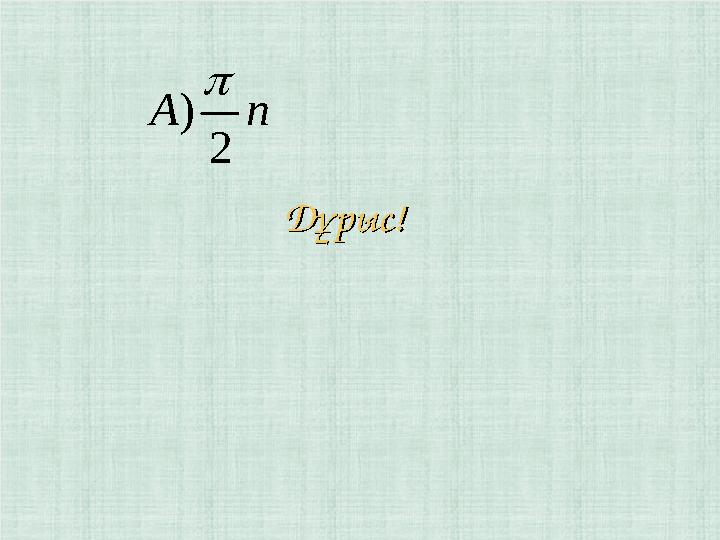
19 слайд
Дұрыс!Дұрыс!n А 2 ) 

19 слайд

20 слайд
ДД ұұ рыс емес!рыс емес! Ойлан!Ойлан!

20 слайд

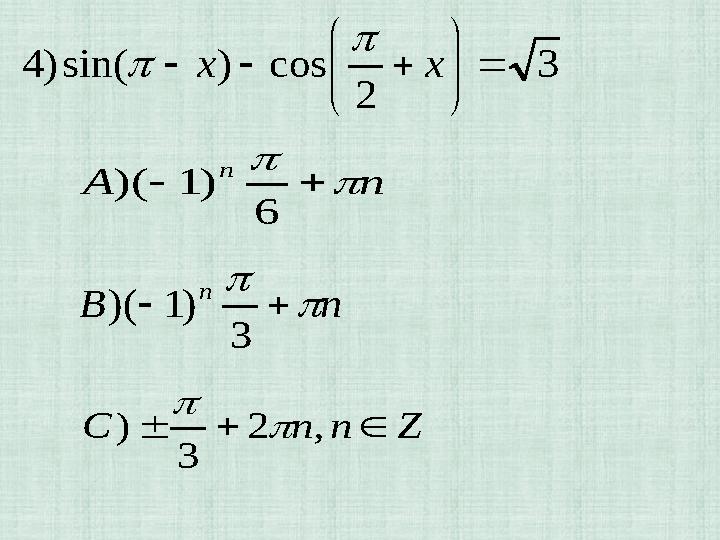
21 слайд
Z n n C    , 2 3 )   n А n     6 ) 1 )( 3 2 cos ) sin( ) 4           x x   n B n     3 ) 1 )(

21 слайд

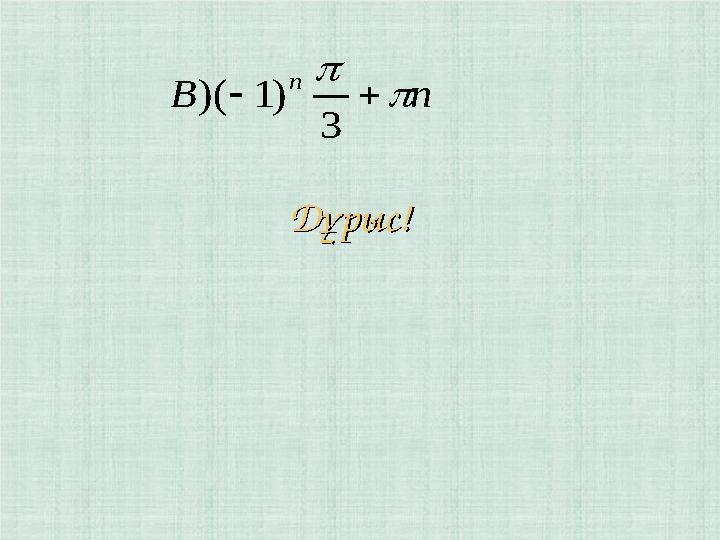
22 слайд
Дұрыс!Дұрыс!n B n     3 ) 1 )(

22 слайд

23 слайд
ДД ұұ рыс емес!рыс емес! Ойлан!Ойлан!

23 слайд

24 слайд
Әртүрлі тригонометриялық теңдеулерді шешу әдістері Алгебралық теңдеулерге келтірілетін теңдеулер Біртектес тригонометриялық теңдеулер Қосымша аргумент енгізу арқылы шешілетін теңдеулер.Тригонометриялық формулаларды түрлендіру жолымен шешілетін теңдеулер Дәрежені төмендету арқылы шешілетін тригонометриялық теңдеулер

24 слайд

25 слайд
Есептер шығаруЕсептер шығару

25 слайд

26 слайд
ҚорытындыҚорытынды 1) 1) ТТ ригонометриялық теңдеулерді шешуде ригонометриялық теңдеулерді шешуде қолданылатын негізгі формулалар мен қолданылатын негізгі формулалар мен әдістерді әдістерді қайталадық.қайталадық. 2)2) Тригонометриялық теңдеулерді шешу Тригонометриялық теңдеулерді шешу дағдысын дағдысын бекіттікбекіттік ..

26 слайд

27 слайд
Тригонометриялық теңдеулерді шешудегі ескертпелер : 1. Егер функцияның аргументтері бірдей болса, онда формулаларды қолдана отырып аргументтерін өзгертпей, бірдей функцияға келтіру керек. Мысалы: 5sin2x+6cosx-6=0 2 .Егер функцияның аргументтерінде екі есе айырмашылық болса, қос бұрыштың формулаларын пайдаланып бірдей аргументке келтіруіміз керек. Мысалы: 1+с os4x=2cos2x , 2sinx+3cos2x-3=0 3. Егер бір аргументтің функцияларының дәрежелері 1- ден жоғары болса, оларды қысқаша көбейту формуласын пайдаланып дәрежесін төмендетуге болады . Мысалы: 4.Аргументтері әртүрлі екінші дәрежелі функциялардың дәрежесін төмендету үшін дәрежені төмендету формуласын пайдаланамыз .) sin )(cos sin (cos cos sin cos sin 2 ) cos (cos cos sin 2 2 2 2 4 4 2 2 2 2 2 4 4 x x x x x x x x x x x x        

27 слайд

28 слайд
                           6 sin 2 cos 6 sin sin 6 cos 2 cos 2 1 sin 2 3 2 cos sin 3    x x x x x x x 5.Аргументтері әртүрлі бірінші дәрежелі синус(косинус) фунцияларының қосындысы берілсе, қосындыны ортақ көбейткіш алу үшін көбейтіндіге түрлендіреміз. Мысалы: sinx+sin2x+sin3x=0 (sinx+sin3x)+sin2x=0 6. Аргументтері әртүрлі бірінші дәрежелі синус және косинус функцияларының қосындысы берілсе келтіру формуласын қолданып, бірдей функцияға келтіреміз де , 5 жағдайды орындаймыз. Мысалы: 8.Егер теңдеуде сандық көбейткіш бар болса, онда оны функцияның бұрыштық мәні ретінде алуға болады.           ) 2 sin 3 sin cos 3 sin x x x x  0 , , ,0 sin cos sin sin ,0 cos sin 2 2       c b a x c x x b x a x b x a 0 cos ,0 cos 2   x x 0 cos cos sin , 0 2    x c x x b áîëñà a7. Егер түріндегі біртектес теңдеулердің екі жағында сәйкесінше бөліп, tgx-қа қатысты алгебралық теңдеуге теңдеуі көбейткіштерге жіктеу тәсілімен шешіледі.Келтіріледі. Егер

28 слайд

29 слайд
Үйге тапсырма:Үйге тапсырма:x x x x x x x x x x x x x 3 cos 2 4 cos 2 cos 1 cos 3 sin sin cos cos sin 2 1 3 cos cos 0 2 sin cos 2 2 2 2 2 2           

29 слайд

30 слайд

30 слайд