Материалдар / Ашық сабаққа презентация алгебра 9 сынып "Кез келген бұрыштардың тригонометриялық функциялары"

Ашық сабаққа презентация алгебра 9 сынып "Кез келген бұрыштардың тригонометриялық функциялары"

Материал туралы қысқаша түсінік

Ашық сабаққа дайын презентация

Жумашева Мейрамгуль Тулеубаевна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

09 Ақпан 2024

212

0 рет жүктелген

Геометрия Ашық сабақ 9 сынып

250 ₸

Бүгін алсаңыз
+13 бонус беріледі
Бұл не?

Бүгін алсаңыз +13 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 41

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд
САБАҚТЫҢ МАҚСАТЫ:САБАҚТЫҢ МАҚСАТЫ:  Бұрыштың градустық және радиандық өлшемдері туралы түсінікті кеңейту .  Кез келген бұрыштың синусы, косинусы, тангенсі мен котангенсі ұғымын тереңдетіп, аргументтердің берілген мәні бойынша тригонометриялық функцияның мәнін табуды үйрену.  Оқушыларға тригонометриялық функцияларға есеп шығаруды меңгерту .

2 слайд

САБАҚТЫҢ МАҚСАТЫ:САБАҚТЫҢ МАҚСАТЫ:  Бұрыштың градустық және радиандық өлшемдері туралы түсінікті кеңейту .  Кез келген бұрыштың синусы, косинусы, тангенсі мен котангенсі ұғымын тереңдетіп, аргументтердің берілген мәні бойынша тригонометриялық функцияның мәнін табуды үйрену.  Оқушыларға тригонометриялық функцияларға есеп шығаруды меңгерту .

3 слайд

4 слайд

5 слайд

6 слайд

7 слайд

8 слайд
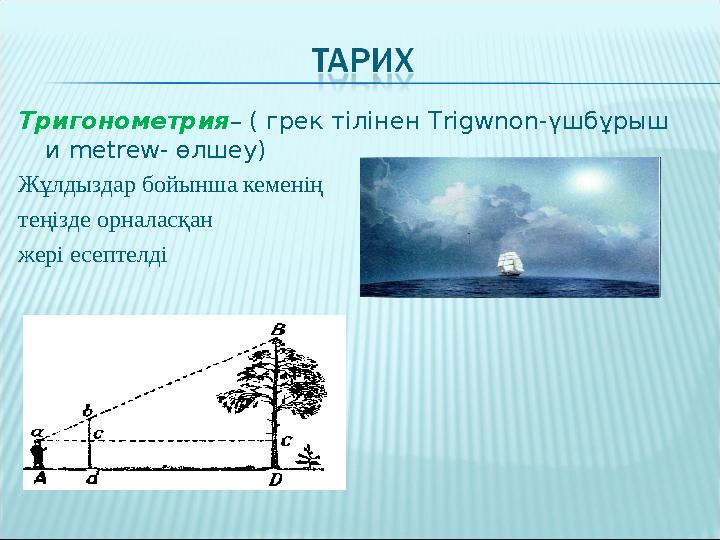
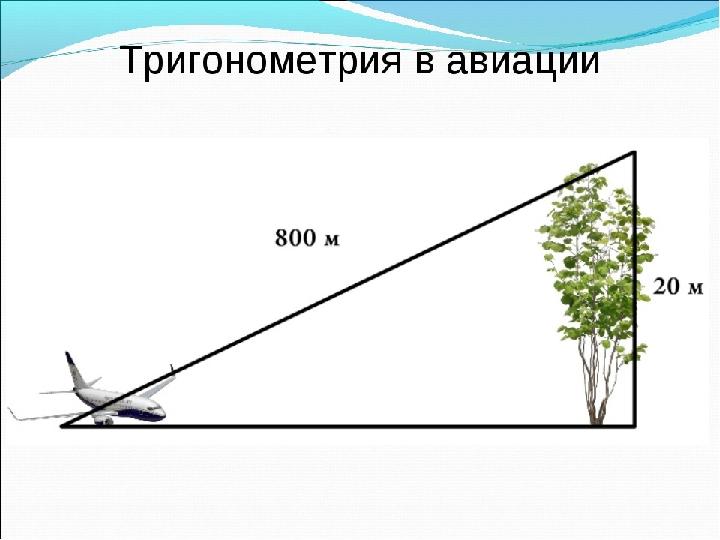
Тригонометрия – ( грек т ілінен T rigwnon-үшбұрыш и metrew- өлшеу) Жұлдыздар бойынша кеменің теңізде орналасқан жері есептелді

8 слайд

Тригонометрия – ( грек т ілінен T rigwnon-үшбұрыш и metrew- өлшеу) Жұлдыздар бойынша кеменің теңізде орналасқан жері есептелді

9 слайд
Улугбек (1394-1449) - Самаркандтағы ғылыми мектебінің қалаушысы Жазыңқы тригонометрияның алғашқы трактаты (X—XI вв.).

9 слайд

Улугбек (1394-1449) - Самаркандтағы ғылыми мектебінің қалаушысы Жазыңқы тригонометрияның алғашқы трактаты (X—XI вв.).

10 слайд
Гиппарх Никейский ( 180 – 125 г. до н.э.) • Таблица числовых значений хорд • Таблица для определения соотношний между элементами треугольников • Первая таблица синусов, высчитанная по хордам в окружности • «Альмагест – самая значимая тригонометрическая работа всей античности Клавдий Птолемей (90 – 168 г н.э)

10 слайд

Гиппарх Никейский ( 180 – 125 г. до н.э.) • Таблица числовых значений хорд • Таблица для определения соотношний между элементами треугольников • Первая таблица синусов, высчитанная по хордам в окружности • «Альмагест – самая значимая тригонометрическая работа всей античности Клавдий Птолемей (90 – 168 г н.э)

11 слайд
• Построил таблицы тангенсов, котангенсов и косекансов • Присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов • Установил основные соотношения между этими линиями • Дал определения функциям • Установил формулу двойного угла Ал-Батани ( ок. 900 г. н.э) Абу-ль-Вефа ( 940 – 997 г. н.э)

11 слайд

• Построил таблицы тангенсов, котангенсов и косекансов • Присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов • Установил основные соотношения между этими линиями • Дал определения функциям • Установил формулу двойного угла Ал-Батани ( ок. 900 г. н.э) Абу-ль-Вефа ( 940 – 997 г. н.э)

12 слайд
Насир-эд-Дин из Туса (1201 – 1274 г. н.э) Ал-Хорези (783 – 850 г. н.э) • Автор трактата о полном четырехстороннике • Построил таблицы синусов и котангенсов

12 слайд

Насир-эд-Дин из Туса (1201 – 1274 г. н.э) Ал-Хорези (783 – 850 г. н.э) • Автор трактата о полном четырехстороннике • Построил таблицы синусов и котангенсов

13 слайд
Франсуа Виет (1540 – 1603 г.) Исаак Ньютон (1643 – 1727г.) • Дополнил и систематизировал различные случаи решения плоских и сферических треугольников • Открыл «плоскую» теорему косинусов и формулы тригонометрических функций от кратных углов • Разложил функции в ряды и открыл путь для их использования в математическом анализе

13 слайд

Франсуа Виет (1540 – 1603 г.) Исаак Ньютон (1643 – 1727г.) • Дополнил и систематизировал различные случаи решения плоских и сферических треугольников • Открыл «плоскую» теорему косинусов и формулы тригонометрических функций от кратных углов • Разложил функции в ряды и открыл путь для их использования в математическом анализе

14 слайд
Леонард Эйлер (1707 – 1783 г. н.э) • Ввел понятие функции и принятую в наши дни символику • Разъяснил вопрос о знаках всех тригонометрических функций любого аргумента Ричард Саусвелл (1888-1970) • Разработал метод проектирования сложных форм в 1920 году ; • Выразил тригонометрические функции как отношение координат x, y, z к длине элемента.

14 слайд

Леонард Эйлер (1707 – 1783 г. н.э) • Ввел понятие функции и принятую в наши дни символику • Разъяснил вопрос о знаках всех тригонометрических функций любого аргумента Ричард Саусвелл (1888-1970) • Разработал метод проектирования сложных форм в 1920 году ; • Выразил тригонометрические функции как отношение координат x, y, z к длине элемента.

15 слайд
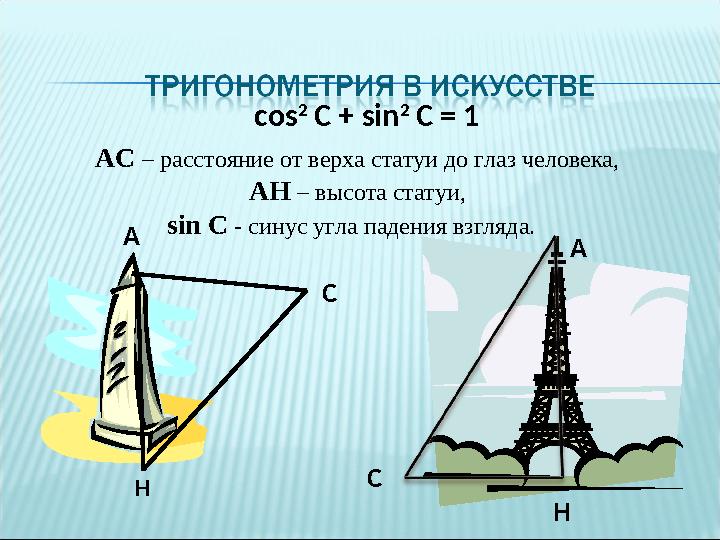
cos 2 С + sin 2 С = 1 АС – расстояние от верха статуи до глаз человека, АН – высота статуи, sin С - синус угла падения взгляда. А С Н А С Н

15 слайд

cos 2 С + sin 2 С = 1 АС – расстояние от верха статуи до глаз человека, АН – высота статуи, sin С - синус угла падения взгляда. А С Н А С Н

16 слайд
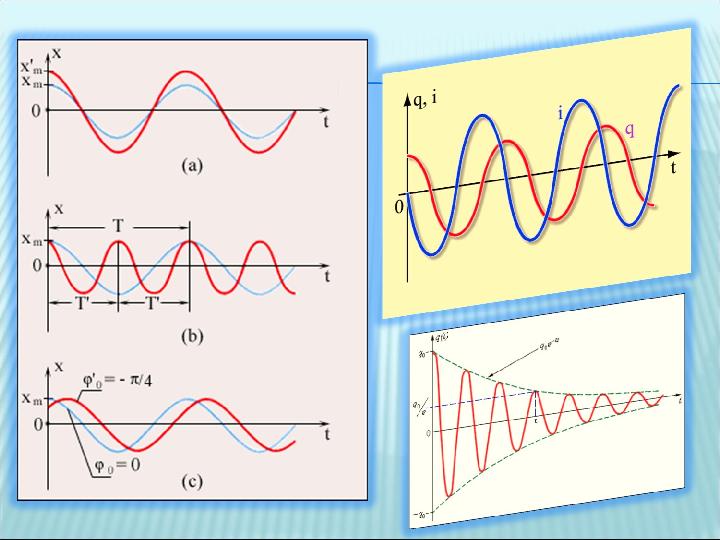
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), называются гармоническими колебаниями . Выражение, стоящее под знаком косинуса или синуса, называется фазой колебания :

16 слайд

Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), называются гармоническими колебаниями . Выражение, стоящее под знаком косинуса или синуса, называется фазой колебания :

17 слайд

18 слайд

19 слайд

20 слайд

21 слайд

22 слайд
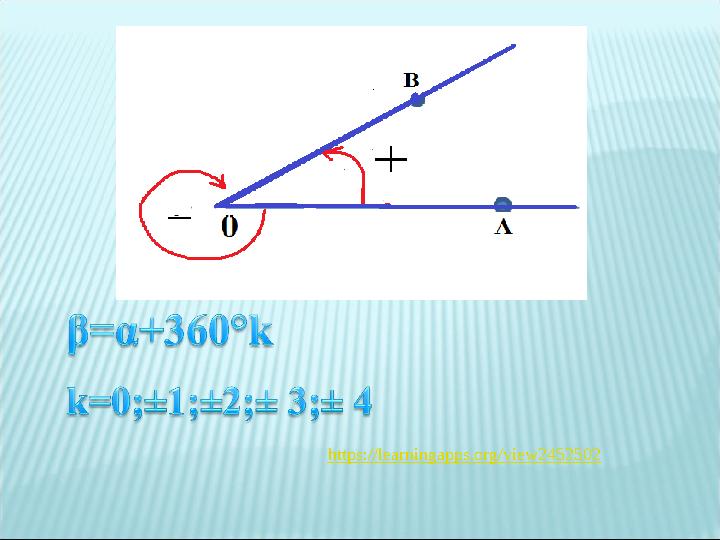
Сұрақ-жауап 1.Жіңішке сұрақтар стратегиясы / иә, жоқ деп жауап беру / 1. Градусты радианға айландыру үшін біз градустық өлшемді π/180 -ге көбейтеміз бе? 2.Бір радиан бұрыш шеңбердің радиусына тең бе? 3 . π - = 180 0 -қа тең бе? 4. π /3 30 0 па? 2. Жуан сұрақтар стратегиясы / сұраққа толық ,әрі түсіндіріп жауап беру / 1.Оң бұрыш деп қандай бұрышты айтады? 2.Теріс бұрыштың оң бұрыштан айырмашылығы неде? 3. Толық айналыс қанша градусқа тең? 4. Кез-келген бұрышты табу үшін қандай формула қолданылады?(формула) 5.Тригонометрияның негізгі тепе-теңдігі? (формула)

22 слайд

Сұрақ-жауап 1.Жіңішке сұрақтар стратегиясы / иә, жоқ деп жауап беру / 1. Градусты радианға айландыру үшін біз градустық өлшемді π/180 -ге көбейтеміз бе? 2.Бір радиан бұрыш шеңбердің радиусына тең бе? 3 . π - = 180 0 -қа тең бе? 4. π /3 30 0 па? 2. Жуан сұрақтар стратегиясы / сұраққа толық ,әрі түсіндіріп жауап беру / 1.Оң бұрыш деп қандай бұрышты айтады? 2.Теріс бұрыштың оң бұрыштан айырмашылығы неде? 3. Толық айналыс қанша градусқа тең? 4. Кез-келген бұрышты табу үшін қандай формула қолданылады?(формула) 5.Тригонометрияның негізгі тепе-теңдігі? (формула)

23 слайд
https://learningapps.org/view2452502

23 слайд

https://learningapps.org/view2452502

24 слайд

25 слайд

26 слайд
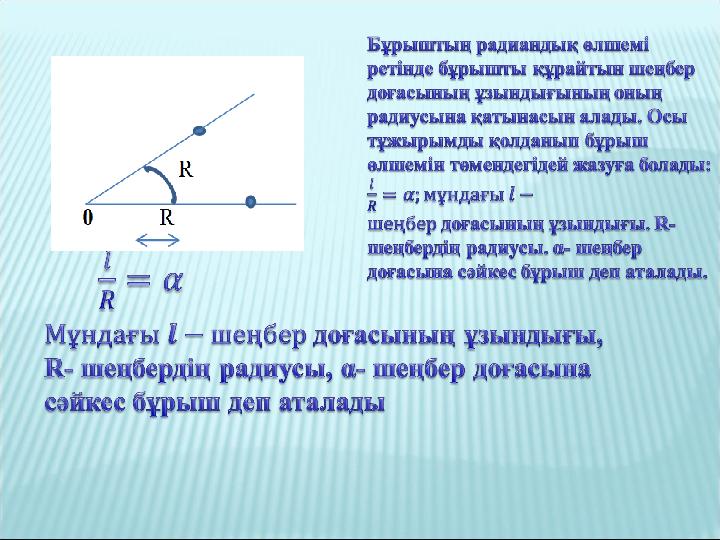
1. Центрі координаталар басында болатын шеңбер. 2. Радиусы 1 тең.y   sin Анықтама: x   cos x y tg   y x ctg  

26 слайд

1. Центрі координаталар басында болатын шеңбер. 2. Радиусы 1 тең.y   sin Анықтама: x   cos x y tg   y x ctg  

27 слайд
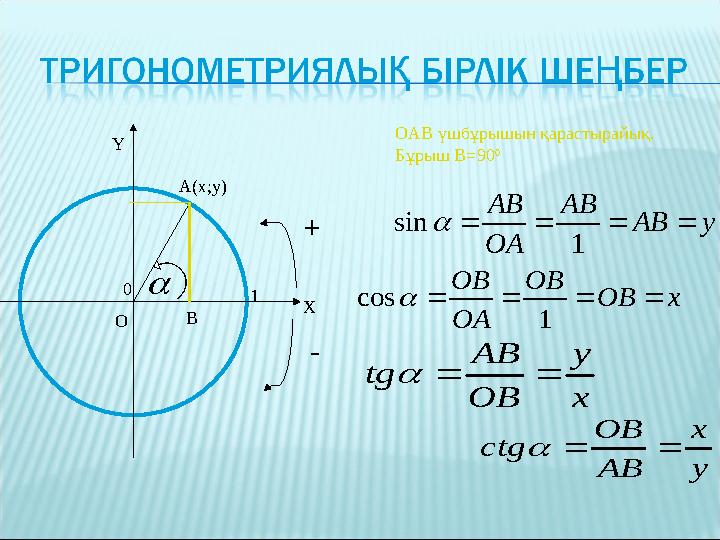
y AB AB OA AB     1 sin  y x AB OB ctg   + -0 1Y X  A(x;y) B OAB үшбұрышын қарастырайық . Бұрыш B=90 0 x OB OB OA OB     1 cos  x y OB AB tg    O

27 слайд

y AB AB OA AB     1 sin  y x AB OB ctg   + -0 1Y X  A(x;y) B OAB үшбұрышын қарастырайық . Бұрыш B=90 0 x OB OB OA OB     1 cos  x y OB AB tg    O

28 слайд
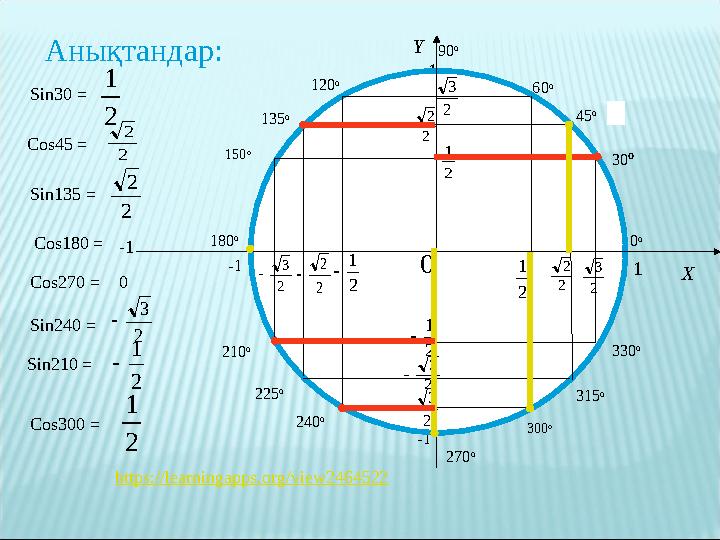
XY 90 o 1-1 1 -1 30 o60 o 120 o 135 o 150 o 180 o 210 o 225 o 240 o 270 o 300 o 330 o 315 o 0 o0 2 1 2 1 2 1  2 1  2 2  2 2  2 2 2 2 2 3 2 3 2 3  2 3 45 oАнықтандар: Sin30 = 2 1 Sin135 =Cos45 = Cos180 = Cos270 = Sin240 = Sin210 = Cos300 = 2 2 2 2 -1 0 2 3  2 1  2 1 https://learningapps.org/view2464522

28 слайд

XY 90 o 1-1 1 -1 30 o60 o 120 o 135 o 150 o 180 o 210 o 225 o 240 o 270 o 300 o 330 o 315 o 0 o0 2 1 2 1 2 1  2 1  2 2  2 2  2 2 2 2 2 3 2 3 2 3  2 3 45 oАнықтандар: Sin30 = 2 1 Sin135 =Cos45 = Cos180 = Cos270 = Sin240 = Sin210 = Cos300 = 2 2 2 2 -1 0 2 3  2 1  2 1 https://learningapps.org/view2464522

29 слайд
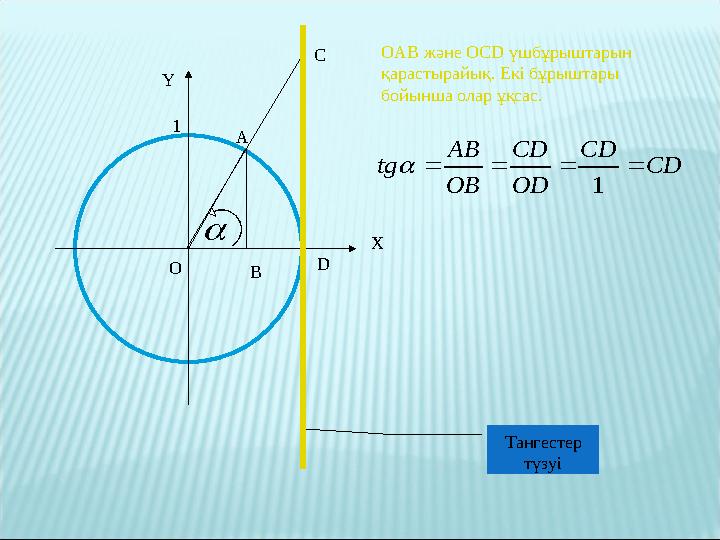
B Тангестер түзуіY  XA O C D1 OAB және OCD үшбұрыштарын қарастырайық . Екі бұрыштары бойынша олар ұқсас. CD CD OD CD OB AB tg     1 

29 слайд

B Тангестер түзуіY  XA O C D1 OAB және OCD үшбұрыштарын қарастырайық . Екі бұрыштары бойынша олар ұқсас. CD CD OD CD OB AB tg     1 

30 слайд
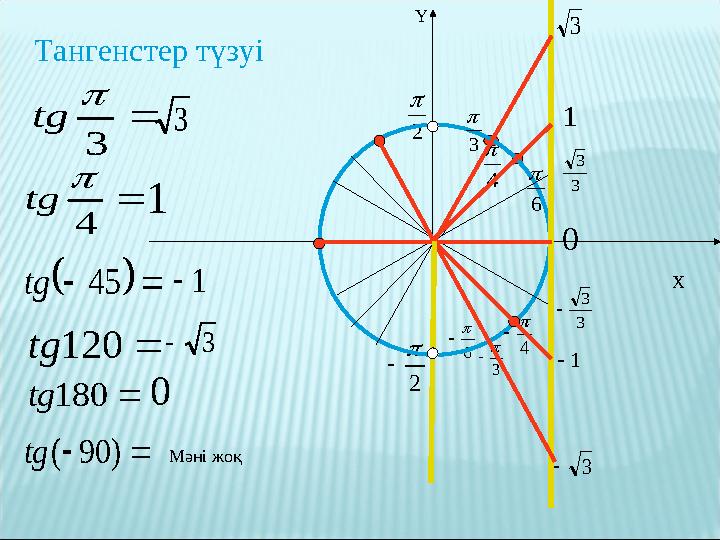
X6   3 3  0 3 3 3 3  1 1 Y 2  2   3   4   4  6  3  Тангенстер түзуі  3  tg 3  4  tg 1     45 tg 1   120 tg 3   180 tg 0   ) 90 ( tg Мәні жоқ

30 слайд

X6   3 3  0 3 3 3 3  1 1 Y 2  2   3   4   4  6  3  Тангенстер түзуі  3  tg 3  4  tg 1     45 tg 1   120 tg 3   180 tg 0   ) 90 ( tg Мәні жоқ

31 слайд
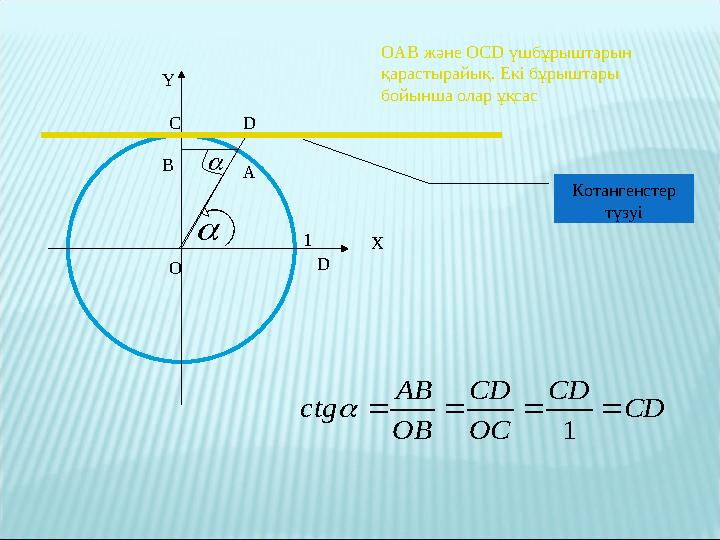
Котангенстер түзуіY  XA O D1 OAB және OCD үшбұрыштарын қарастырайық . Екі бұрыштары бойынша олар ұқсас B C D  CD CD O С CD OB AB сtg     1 

31 слайд

Котангенстер түзуіY  XA O D1 OAB және OCD үшбұрыштарын қарастырайық . Екі бұрыштары бойынша олар ұқсас B C D  CD CD O С CD OB AB сtg     1 

32 слайд
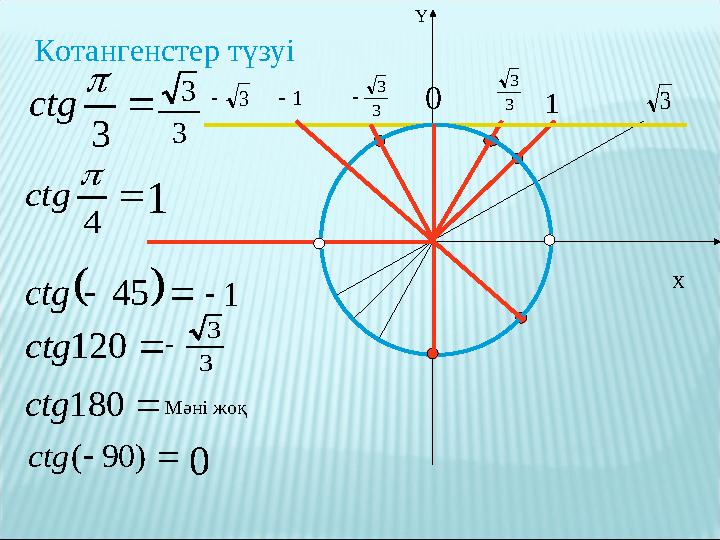
X3 3  0 3 3 3 3  1 1 Y Котангенстер түзуі 1 1  0 Мәні жоқ  3  сtg  4  сtg     45 сtg  120 сtg  180 сtg   ) 90 ( сtg 3 3 3 3 

32 слайд

X3 3  0 3 3 3 3  1 1 Y Котангенстер түзуі 1 1  0 Мәні жоқ  3  сtg  4  сtg     45 сtg  120 сtg  180 сtg   ) 90 ( сtg 3 3 3 3 

33 слайд
І деңгей : 1. ІІ деңгей: 1. 2. 3. 4. ІІІ деңгей: 1. 2. 3. 4.

33 слайд

І деңгей : 1. ІІ деңгей: 1. 2. 3. 4. ІІІ деңгей: 1. 2. 3. 4.

34 слайд

35 слайд
1. А) 105 0 қай ширекке тиісті? В) 3sin30 0 - 4cos270 0 +tg45 0 C) ctg45 0 +ctg60 0 +ctg30 0 2. А) 215 0 қай ширекке тиісті? В) 3sin30 0 +2/√3sin60 0 +1 C) 2cos60 0 +4sin30 0 +5cos0 0 3. А) 340 0 қай ширекке тиісті? В) 3sin60 0 - 1/2ctg45 0 C) 5cos270 0 +2sin30 0 +3ctg90 0 4. А) 160 0 қай ширекке тиісті? В) 3sin60 0 - 1/2tg45 0 +tg45 0

35 слайд

1. А) 105 0 қай ширекке тиісті? В) 3sin30 0 - 4cos270 0 +tg45 0 C) ctg45 0 +ctg60 0 +ctg30 0 2. А) 215 0 қай ширекке тиісті? В) 3sin30 0 +2/√3sin60 0 +1 C) 2cos60 0 +4sin30 0 +5cos0 0 3. А) 340 0 қай ширекке тиісті? В) 3sin60 0 - 1/2ctg45 0 C) 5cos270 0 +2sin30 0 +3ctg90 0 4. А) 160 0 қай ширекке тиісті? В) 3sin60 0 - 1/2tg45 0 +tg45 0

36 слайд
1 . α бұрышы қай ширекке тиісті,мұндағы α= А. I В. I және II С. III Д. II және III Е. IV 2 . 2 cos60 0 +cos30 0 өрнегінің мәнін есепте: А. 15 В. 0 С. 2,5 Д. 25 Е. 1,5 3 . Мәнін тап: cos90° А. -0,5 В. -1 С. 0 Д. 1 Е. 0,5 4 . Мәнін тап sin450° А. 2 В. -1 С. 1 Д. Е. 0 5 . COS өрнегінің мәні: А. В. С. Д. Е.1

36 слайд

1 . α бұрышы қай ширекке тиісті,мұндағы α= А. I В. I және II С. III Д. II және III Е. IV 2 . 2 cos60 0 +cos30 0 өрнегінің мәнін есепте: А. 15 В. 0 С. 2,5 Д. 25 Е. 1,5 3 . Мәнін тап: cos90° А. -0,5 В. -1 С. 0 Д. 1 Е. 0,5 4 . Мәнін тап sin450° А. 2 В. -1 С. 1 Д. Е. 0 5 . COS өрнегінің мәні: А. В. С. Д. Е.1

37 слайд
1. 1. А А 2.2. С С 3.3. С С 4.4. С С 5.5. В В

37 слайд

1. 1. А А 2.2. С С 3.3. С С 4.4. С С 5.5. В В

38 слайд

39 слайд

40 слайд