Ашық сабаққа презентация, Тригонометриялық функциялардың қасиеттері мен графиктері

1 слайд

1 слайд

2 слайд
Сабақ мақсаты • Оқытушылық: Тригонометриялық функциялардың қасиеттерімен таныстырып, графиктерін тұрғызуға үйрету, тригонометриялық функциялардың графиктерін түрлендіруді иллюстративті түрде көрсету

2 слайд

3 слайд
Сабақ мақсаты • Дамытушылық: Білімгерлердің логикалық ойлауын, есте сақтау қабілетін, дұрыс шешім қабылдау қасиетін, математикалық білімін, меңгерген білімін пайдалану қабілетін, математикалық сауаттылығын дамыту. Тригонометриялық функциялардың қаситтерін пайдаланып олардың графиктерін тұрғызу машығы мен икемділігін дамыту

3 слайд

4 слайд
Сабақ мақсаты • Тәрбиелік: патриоттық сезімдерін қалыптастыруға, толеранттылыққа, өзін және өзгені сыйлауға, еңбекқорлыққа, өзгенің еңбегін бағалай білуге, ұқыптылыққа, шыдамдылыққа, төзімділікке, белсенділікке, шапшаңдыққа, парасаттылыққа, тазалыққа, жауапкершілікті болуға тәрбиелеу

4 слайд

5 слайд
САБАҚ ЖОСПАРЫ: 1.Ұйымдастыру кезеңі 2.Білімді белсендіру 3.Жаңа білімді игерту 4.Меңгерілген білімді бекіту 5.Үй тапсырмасы туралы ақпарат беру

5 слайд

6 слайд
ЖАҢА ТАҚЫРЫПТЫ МЕҢГЕРТУ 1.Синус функциясының қасиеттері мен графигі. 2.Синус функциясының графигін түрлендіру мысалдары 3. Косинус функциясының қасиеттері мен графигі 4.Косинус функциясының графигін түрлендіру мысалдары 5. Тангенс функциясының қасиеттері мен графигі 6.ангенс функциясының графигін түрлендіру мысалдары 7. Котангенс функциясының қасиеттері мен графигі 8.Котангенс функциясының графигін түрлендіру мысалдары 9.Пән аралық байланыс

6 слайд

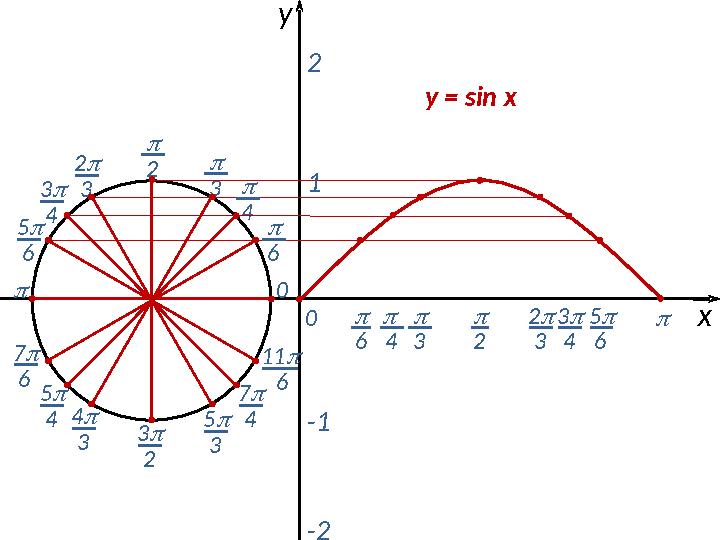
7 слайд
3 22  3 5  6  0 7  6 4  3 3  2 5  3 11  6  6  3 2  3 5  6 0 4 7  4  4 3  4 х 5  43  4 y = sin xy 12 -1 -2  2 6

7 слайд

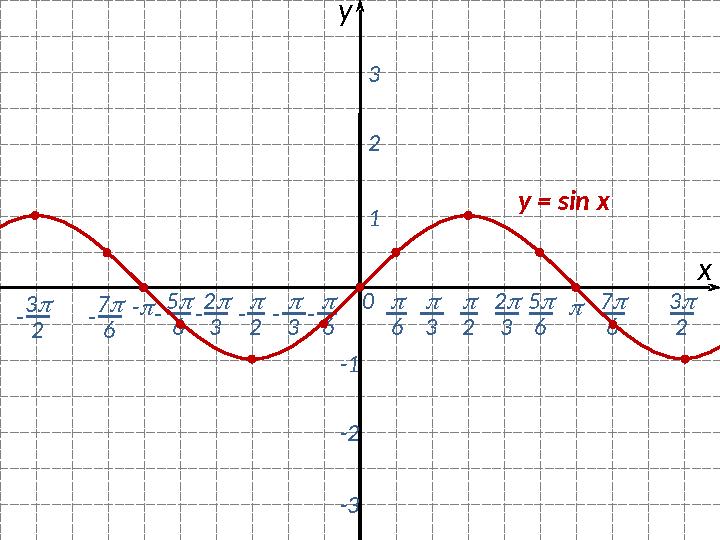
8 слайд
2 0 хy  6  3 2  3 5  6 6--  3-  2-  123 -1 -2 -3- 2  3- 5  6- 3  2 - 7  6 7  6 3  2y = sin x

8 слайд

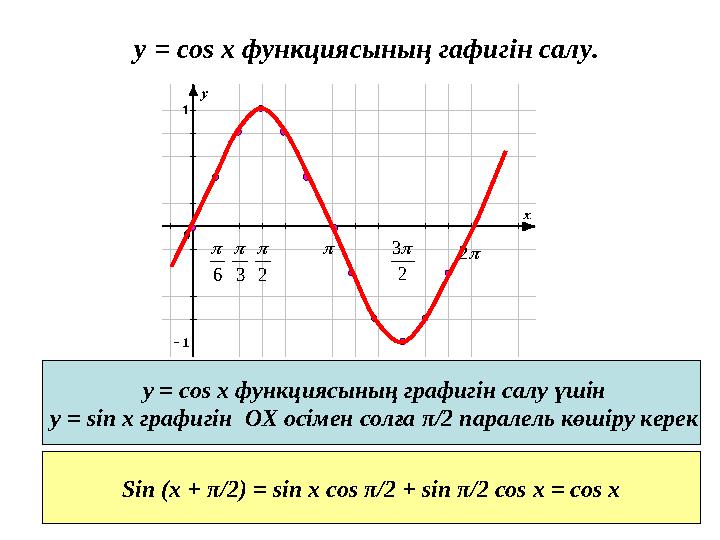
9 слайд
y = cos x функциясының гафигін салу.2  6  3   2 2 3 у = cos x функциясының графигін салу үшін у = sin x графигін ОХ осімен солға π /2 паралель көшіру керек Sin (x + π /2) = sin x cos π /2 + sin π /2 cos x = cos x

9 слайд

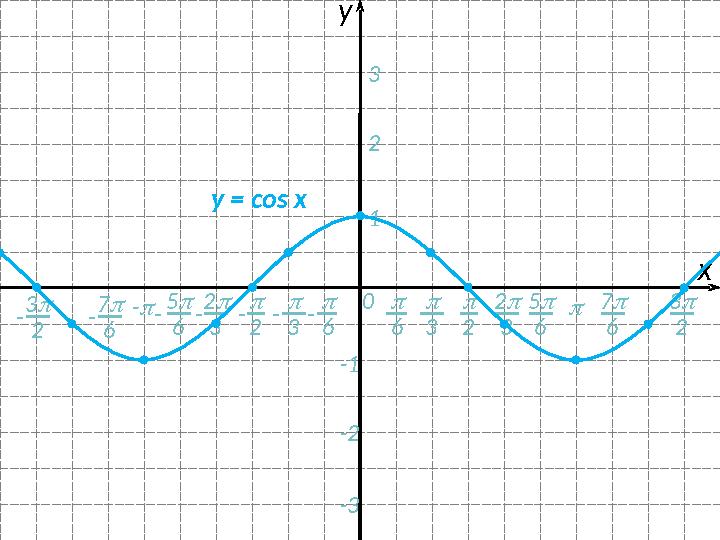
10 слайд
2 0 хy  6  3 2  3 5  6 6--  3-  2-  123 -1 -2 -3- 2  3- 5  6- 3  2 - 7  6 7  6 3  2y = соs x

10 слайд

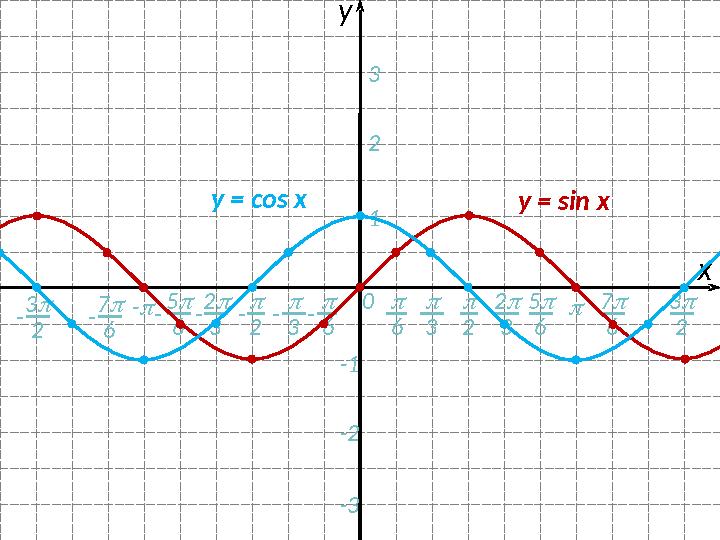
11 слайд
2 0 хy  6  3 2  3 5  6 6--  3-  2-  123 -1 -2 -3- 2  3- 5  6- 3  2 - 7  6 7  6 3  2y = sin xy = соs x

11 слайд

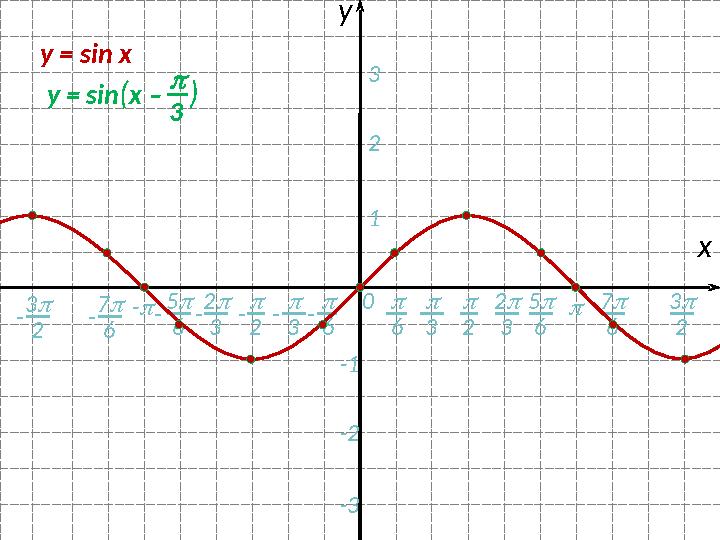
12 слайд
0 -  - 2  3  6 6- 7  6- 5  6  2 хy  3 2  3 5  6-  3-  2 123 -1 -2 -3- 3  2 - 7  6 3  2y = sin x y = sin ( x  ) 3 

12 слайд

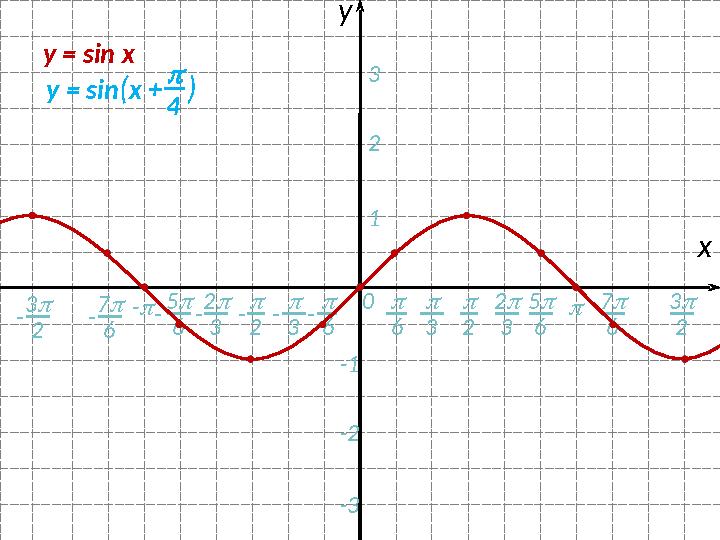
13 слайд
0 -  - 2  3  6 6- 7  6- 5  6  2 хy  3 2  3 5  6-  3-  2 123 -1 -2 -3- 3  2 - 7  6 3  2y = sin x y = sin ( x + ) 4 

13 слайд

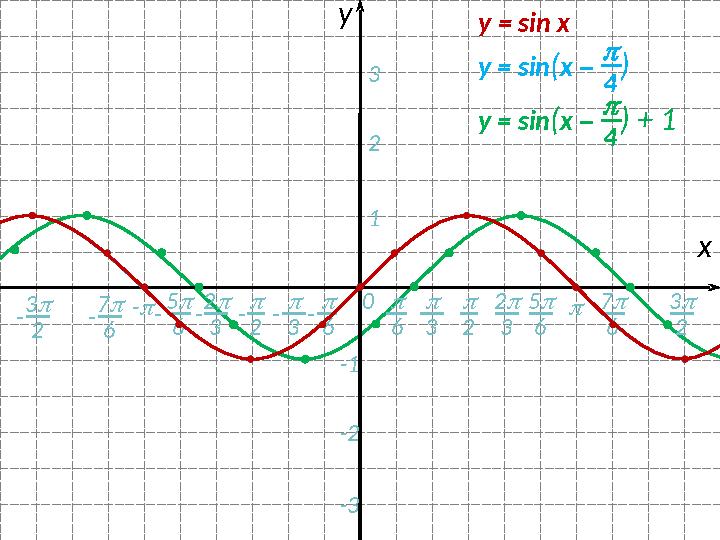
14 слайд
0 -  - 2  3  6 6- 7  6- 5  6  2 хy  3 2  3 5  6-  3-  2 123 -1 -2 -3- 3  2 - 7  6 3  2y = sin x y = sin ( x – ) 4  y = sin ( x – ) + 1 4 

14 слайд

15 слайд
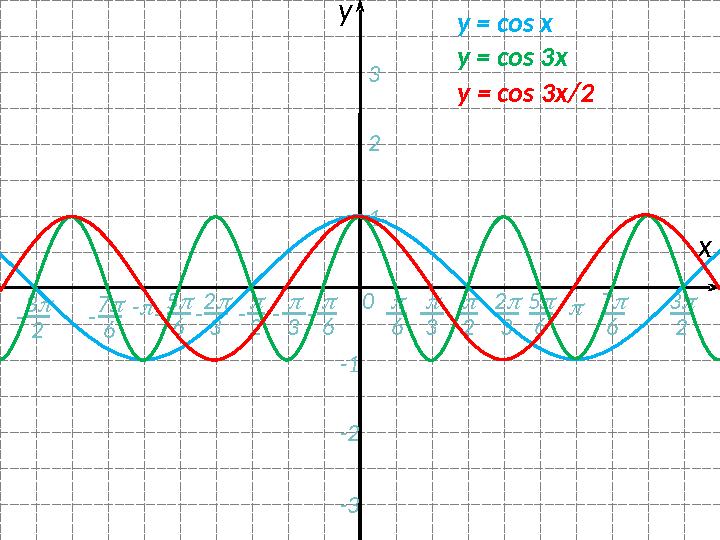
0 -  - 2  3  6 6- 7  6- 5  6  2 хy  3 2  3 5  6-  3-  2 123 -1 -2 -3- 3  2 - 7  6 3  2y = соs x y = соs 3x y = соs 3x/2

15 слайд

16 слайд
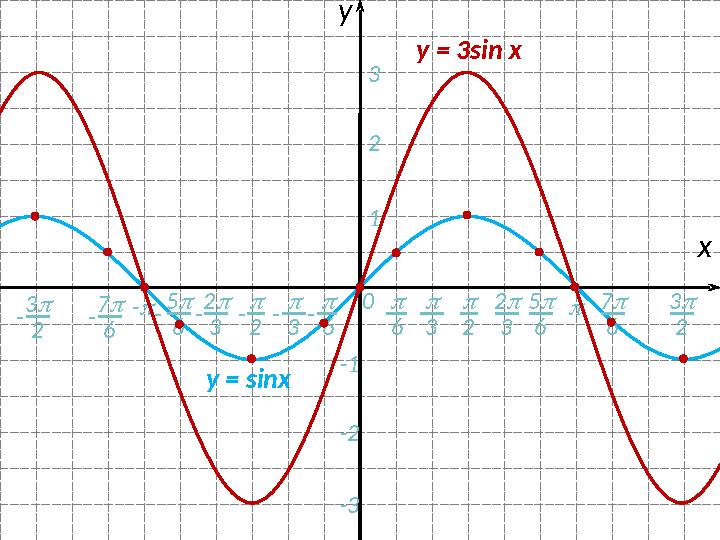
0 -  - 2  3  6 6- 7  6- 5  6  2 хy  3 2  3 5  6-  3-  2 123 -1 -2 -3- 3  2 - 7  6 3  2y = 3sin x y = sinx

16 слайд

17 слайд
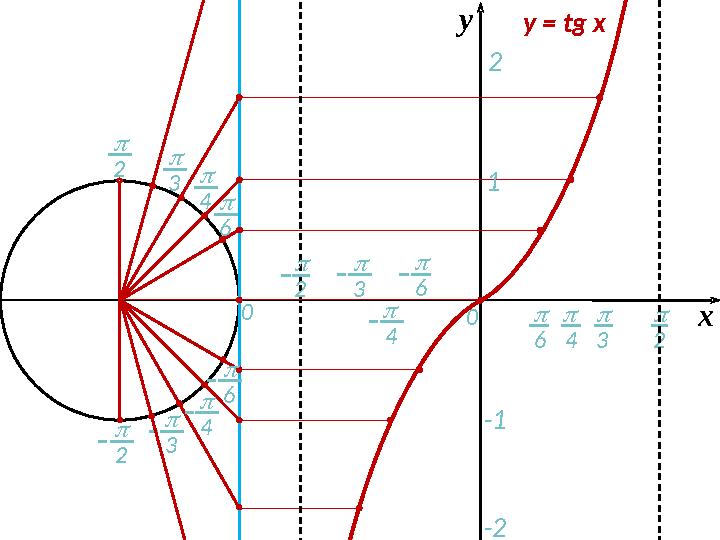
 3  2  3 2 0  6  30 4  4 хy = tg xy 1 2 -1 -2  2 6  4  6  4 2  6  3

17 слайд

18 слайд
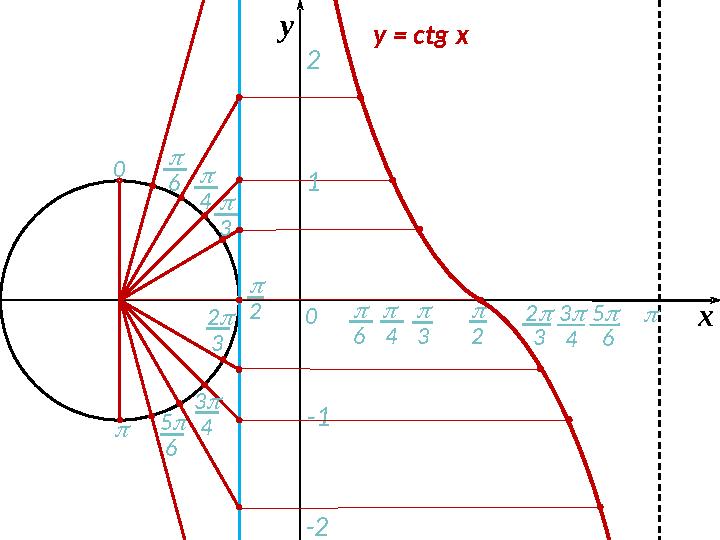
5 6   60 2  3 5  60 4 3  4 хy = с tg xy 1 2 -1 -2 3 3  4 2  3  4  2  3 6  2

18 слайд

19 слайд
Физика сабақтарында гармониялық тербелістерді оқиды. Оларды синус және косинус функциялары арқылы келесі заңдылықтармен анықтайды:    J t ACos t f      J t ASin t f    мұндағы A – тербеліс амплитуда сы w – тербеліс жиілігі J – бастапқы фаза (t = 0 болғандағы бастапқы орын ) фазалық бұрыш Фаза -тербеліс және толқын процессін сипаттайтын периодты өзгеретін функция аргументі. Аргументті, яғни фазаны π/2-ге жылжытқанда синус пен косинус беттесетін болғандықтан келісім бойынша фаза деп косинустың аргументін аламыз. Амплитуда – синусоиданың максималды мәні. Пән аралық байланыс

19 слайд

20 слайд
Жаңа тақырыпты түсінгенін тексеру Әр топқа арналған сұрақтарға жауап алу 1. y= sinx, y=cosx, y=tg x, y=ctg x функцияларының анықталу облысы 2. y= sinx, y=cosx, y=tg x, y=ctg x функцияларының мәндер жиыны 3.Тригонометриялық функциялардың периодтылығы 4.Тригонометриялық функциялардың өспелі, кемімелі аралықтары 5.Тригонометриялық функциялардың қасиеттері 6.Тригонометриялық функциялардың графиктеріндегі қатені табу

20 слайд

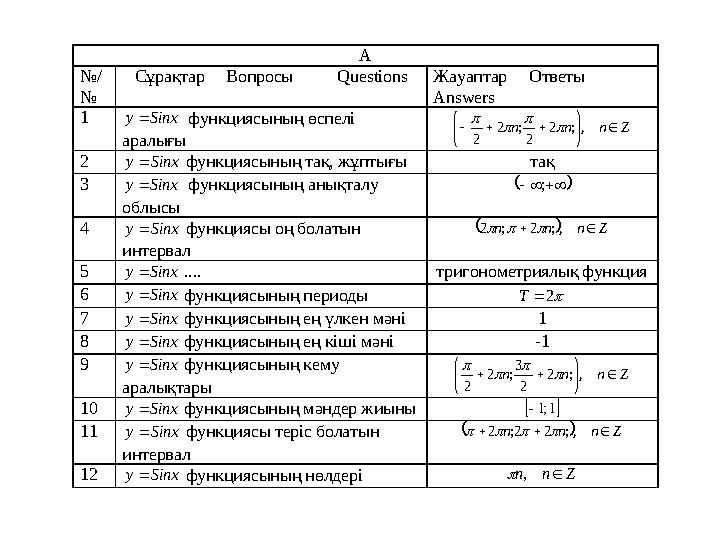
21 слайд
А №/ № Сұрақтар Вопросы Q uestions Жауаптар Ответы Answers 1 Sinx y  функциясының өспелі аралығы Z n n n           , ; 2 2 ; 2 2     2 Sinx y  функциясының тақ, жұптығы тақ 3 Sinx y  функциясының анықталу облысы      ; 4 Sinx y  функциясы оң болатын интервал   Z n n n   ,; 2 ; 2    5 Sinx y  .... тригонометриялық функция 6 Sinx y  функциясының периоды 2  T 7 Sinx y  функциясының ең үлкен мәні 1 8 Sinx y  функциясының ең кіші мәні -1 9 Sinx y  функциясының кему аралықтары Z n n n          , ; 2 2 3; 2 2     10 Sinx y  функциясының мәндер жиыны  1;1 11 Sinx y  функциясы теріс болатын интервал   Z n n n    ,; 2 2; 2     12 Sinx y  функциясының нөлдері Z n n  , 

21 слайд

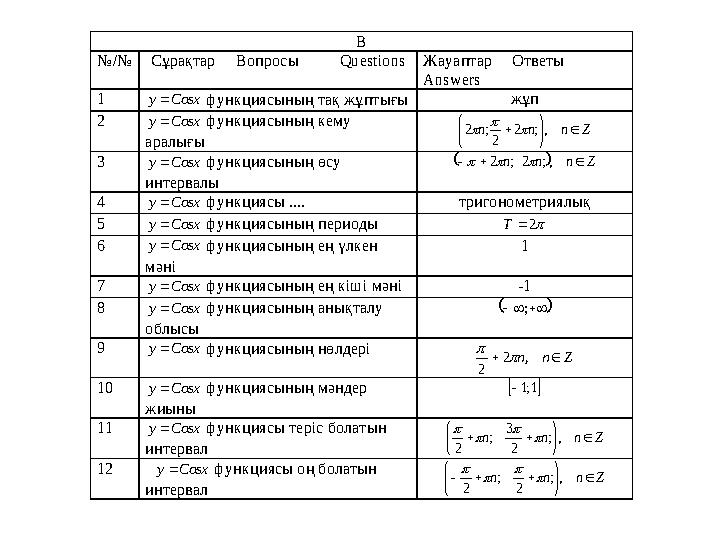
22 слайд
В №/№ Сұрақтар Вопросы Q uestions Жауаптар Ответы Answers 1 Cosx y  функциясының тақ жұптығы жұп 2 Cosx y  функциясының кему аралығы Z n n n         ,; 2 2 ; 2    3 Cosx y  функциясының өсу интервалы   Z n n n    ,; 2 ; 2    4 Cosx y  функциясы .... тригонометриялық 5 Cosx y  функциясының периоды 2  T 6 Cosx y  функциясының ең үлкен мәні 1 7 Cosx y  функциясының ең кіші мәні -1 8 Cosx y  функциясының анықталу облысы      ; 9 Cosx y  функциясының нөлдері Z n n   , 2 2   10 Cosx y  функциясының мәндер жиыны  1;1 11 Cosx y  функциясы теріс болатын интервал Z n n n          ,; 2 3 ; 2     12 Cosx y  функциясы оң болатын интервал Z n n n           ,; 2 ; 2    

22 слайд

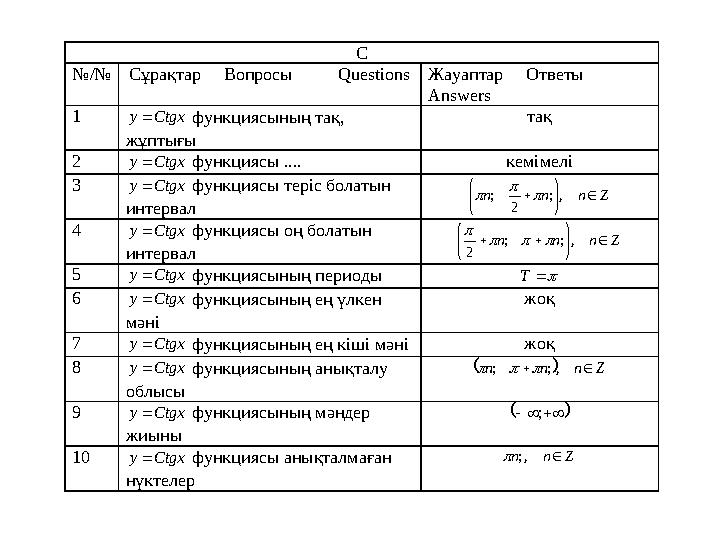
23 слайд
С №/№ Сұрақтар Вопросы Q uestions Жауаптар Ответы Answers 1 Ctgx y  функциясының тақ, жұптығы тақ 2 Ctgx y  функциясы .... кемімелі 3 Ctgx y  функциясы теріс болатын интервал Z n n n         , ; 2 ;    4 Ctgx y  функциясы оң болатын интервал Z n n n          , ; ; 2     5 Ctgx y  функциясының периоды   T 6 Ctgx y  функциясының ең үлкен мәні жоқ 7 Ctgx y  функциясының ең кіші мәні жоқ 8 Ctgx y  функциясының анықталу облысы   Z n n n   ,; ;    9 Ctgx y  функциясының мәндер жиыны      ; 10 Ctgx y  функциясы анықталмаған нүктелер Z n n  ,; 

23 слайд

24 слайд
Д №/№ Сұрақтар Вопросы Q uestions Жауаптар Ответы Answers 1 tgx y  функциясының тақ жұптығы тақ 2 tgx y  функциясы өспелі 3 tgx y  оң болатын интервал Z n n n         , ; 2 ;    4 tgx y  теріс болатын интервал Z n n n          , ; ; 2    5 tgx y  функциясының периоды   T 6 tgx y  функциясының ең үлкен мәні жоқ 7 tgx y  функциясының ең кіші мәні жоқ 8 tgx y  анықталу облысы Z n n n           , ; 2 ; 2     9 tgx y  мәндер облысы      ; 10 tgx y  анықталмаған нүктелер Z n n  ; 2 

24 слайд

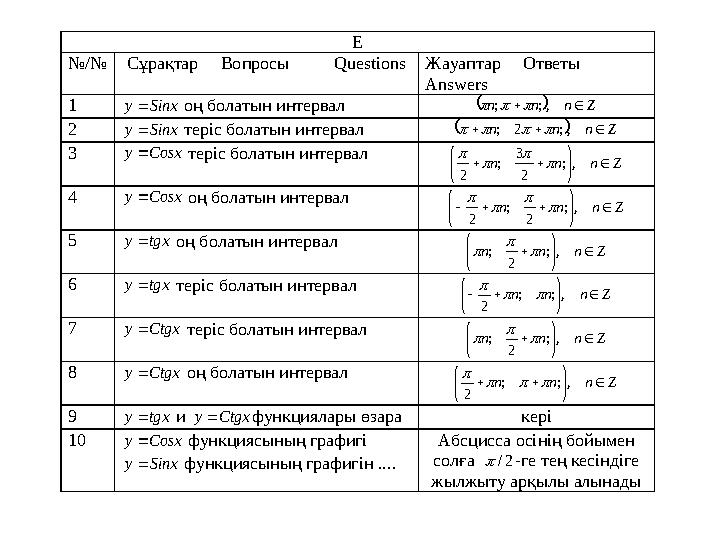
25 слайд
Е №/№ Сұрақтар Вопросы Q uestions Жауапт ар Ответы Answers 1 Sinx y  оң болатын интервал   Z n n n   ,; ;    2 Sinx y  теріс болатын интервал   Z n n n    ,; 2 ;     3 Cosx y  теріс болатын интервал Z n n n          , ; 2 3 ; 2     4 Cosx y  оң болатын интервал Z n n n           , ; 2 ; 2     5 tgx y  оң болатын интервал Z n n n         , ; 2 ;    6 tgx y  теріс болатын интервал Z n n n          , ; ; 2    7 Ctgx y  теріс болатын интервал Z n n n         , ; 2 ;    8 Ctgx y  оң болатын интервал Z n n n          , ; ; 2     9 tgx y  и Ctgx y  функциялары өзара кері 10 Cosx y  функциясының графигі Sinx y  функциясының графигін ... . Абсцисс а осінің бойымен солға 2/  -ге тең кесіндіге жылжыту арқылы алынады

25 слайд

26 слайд
Т ригонометри ялық фу нкциялардың графиктерін түрлендіру А. Cosx y 2  функциясының графигі Cosx y  функциясының графигін ординат а осін ің бойымен 2 есе .... арқылы алынады 1) созу 2) солға жылжыту 3) сығу 4) оңға жылжыту 5)параллель көшіру В. Sinx y 2  функциясының графигі абцисса осіне қатысты ... функциясының графигіне симметр иялы 1) Sinx y 2  2) Sinx y 2   3) Sinx y  4) Sinx y   5)  x Sin y   С. x Sin y 2  функциясының графигі Sinx y  функциясының графигін абсцисс а осінің бойымен 2 есе .... арқылы алы нады 1) созу 2) солға жылжыту 3) сығу 4) оңға жылжыту 5)параллель көшіру Д.         4  x Sin y функци ясының графигі Sinx y  синусоидасын абсцисс а осінің бойымен ұзындығы ... тең болатын кесіндіге солға жылжыту арқылы алынады 1) 3  2) 2  3) 4   4) 4  5) 6  Е. Sinx y  синусоидасын ордината осіні ң бойымен 3 есе созу арқылы, абсцисса осінің бойымен 2 есе сығу арқылы және солға қарай ұзындығы 12/  -ге тең кесіндіге жылжыту арқылы алынған функция 1)         12 3 3  x Sin y 2)         12 2 3  x Sin y 3)         12 3 2  x Sin y 4)          12 2 3  x Sin y 5)         12 2 3  x Sin y

26 слайд

27 слайд
Үйге тапсырма беру Алгебра және анализ бастамалары, Колмогоров А.Н. № 48 (б,в), №56 (а,в)Үйге тапсырма беру

27 слайд