Бас жиын және таңдама. Дискретті және интервалды вариациялық қатар.

1 слайд
Жамбыл политехникалық жоғары колледжі Математика пәнінің оқытушысы Жұмабаев Қайрат Жандарбекұлы Тақырыбы :     Бас жиын және таңдама. Дискретті және интервалды вариациялық қатарлар Мақсаты:        Студенттерге бас жиын және таңдама, интервалды вариациялық қатарлардың анықтамасын және зерттеу обьектілері ретінде статистикалық жиынтық пен таныстыру.

1 слайд

2 слайд
Жоспары. 1.Бас және таңдамалы жиындықтар туралы ұғым. 2. Вариациялық қатар. Зерттеуге жататын барлық объектілердің немесе бір объектіге бірдей жағдайларды жүр- гізілетін барлық бақылаудың мүмкін болатын нәтижелерінің жиынтығы бас жиындық деп аталады. Бас жиындықтан кездейсоқ түрде іріктелген объектілер жиынтығы немесе объектіні бақылау нәтижелерінің жиынтығы таңдама жиындық немесе таңдау деп аталады. Мысалы. 16 жастағы балалар бойының ұзындығын зерттегенде кездейсоқ таңдама колледжінің 16 жастағы балалары болсын. Бас жиынтық – 16 жастағы бар- лық балалар. Кездейсоқ таңдама – бас жиынтықтан таңда- лынған 16 жастағы бойының ұзындықтары бірдей балалар.3 .Вариациялық қатардың құрылымдық сипаттамасы. 4.Дискретті және интервалды вариациялық қатарлар

2 слайд

3 слайд
Бас жиынтық деп белгілі қасиеттерімен бірігетін барлық қарастырылып отырған объектілер жиыны. Мысалы. 1. Егер бір кәсіпорынды алатын болсақ, онда жеке жұмысшы объект болады да, ал кәсіпорынның барлық жұмысшылары бас жиындық болады. 2. Студенттердің жасаған телефон қоңырауларының санын зерттеу үшін, топта оқитын 25 студенттен сұхбат алынды. Студенттер жиынтығы - бас жиынтық, топта оқитын 25 студент - таңдама . Кездейсоқ алынған объектілердің жиынын таңдама дейміз. Таңдамаларға жататын жиынды бас жиын дейміз. Таңдаманың ( бас жиынның ) көлемі деп сол жиынындағы объектілер немесе бақылаулар саны. Мысалы. Егер 1000 лампаны тексеру үшін 100 лампыны бөліп алын- са, онда бас жиынның көлемі N= 1000, ал таңдамалы жиындығының көлемі n= 100.

3 слайд

4 слайд
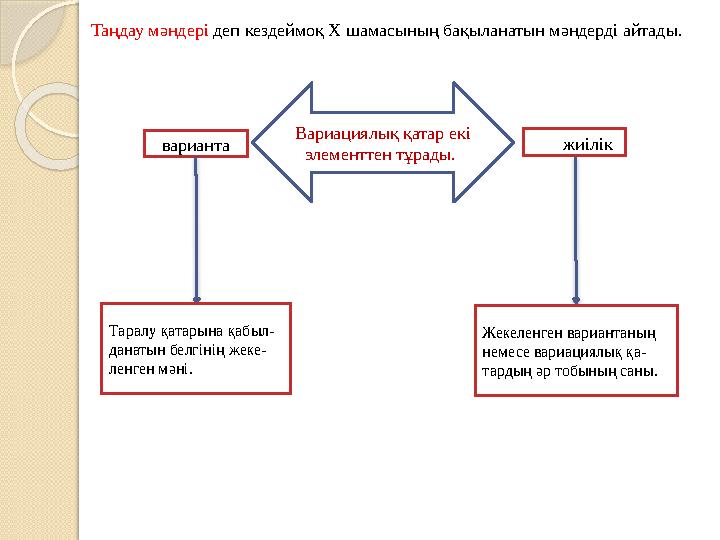
Таңдау мәндері деп кездеймоқ Х шамасының бақыланатын мәндерді айтады. Вариациялық қатар екі элементтен тұрады. варианта жиілік Таралу қатарына қабыл- данатын белгінің жеке- ленген мәні. Жекеленген вариантаның немесе вариациялық қа- тардың әр тобының саны.

4 слайд

5 слайд
Мысал. ,1x ,2x kx ,...,3x қатарын қарастырайық. Мұнда ,1x вариантасы рет, ,2x вариантасы 1n 2n рет, 3x вариантасы 3n рет берілсін және т.с.с. Сонда n саны ( мұндағы  n 2n  ... 3n )kn варианта көлемі болып табылады. 1n in мәні - ,1x іx вариантасының жиілігі, ал n n1 -салыстырмалы жиіліктің саны. Төмендегі кесте жиіліктің статистикалық қатарын береді: Варианта … Варианта жиілігі … 1x 2x kx 1n 2n kn Салыстырмалы жиілігі берілген вариантаның кестесін құрастыру: варианта … салыстырмалы жиілігі … іx n n1 1x 2x kx n nі n nі n n1 n n2 n nk кестені салыстырмалы жиіліктің вариациялық қатары деп аталады. (*) (**)  (**)

5 слайд

6 слайд
Координаталары топтастыру интервалдарының орташа мәндері мен осы интервалдың салыстырмалы жиілігіне сәйкес нүктелерді қосатын сынық салыстырмалы жиіліктің полигоны деп аталады. Салыстырмалы жиіліктің полигонын координаталық жазықтықта салу үшін ), ; ( 1 1 n n х ),..., ; ( 2 2 n n х ) ; ( n n х k k нүктелерін белгілеп, кесінділерді қосамыз. 1-мысал. 8, 9, 4, 8, 6, 8, 8, 9, 4, 4, 4, 9, 6, 9, 9, 4, 8, 8, 8, 9 сандар қатары берілген. Таңдама көлемін, таңдама варианталарын табыңдар; жиіліктің және салыс- тырмалы жиіліктің вариациялық қатарын құрастырыңдар; жиілік полигонын салыңдар. Шешуі. Есептің шарты бойынша таңдама көлемі 20-ға тең. Берілген қатарда 4, 6, 8, 9 сандары кездеседі. Олар таңдама варианталары болып табылады. 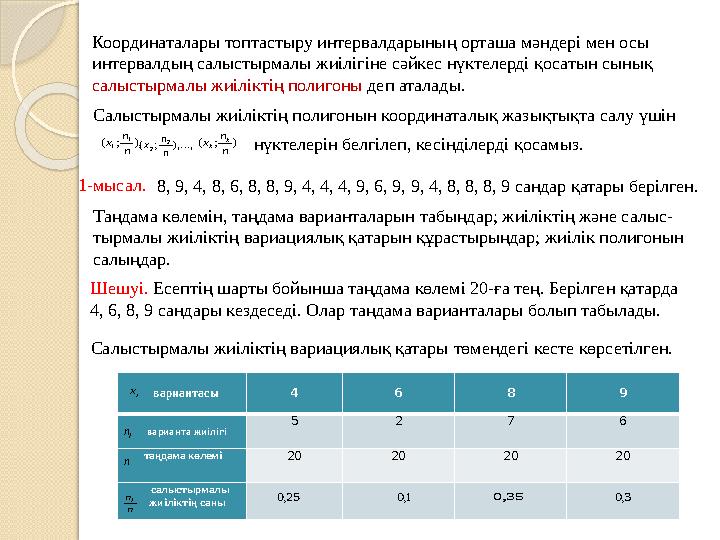Салыстырмалы жиіліктің вариациялық қатары төмендегі кесте көрсетілген. вариантасы 4 6 8 9 варианта жиілігі 5 2 7 6 таңдама көлемі 20 20 20 20 салыстырмалы жиіліктің саны іх n nі 25,0 1,0 35,0 3,0 in n

6 слайд

7 слайд
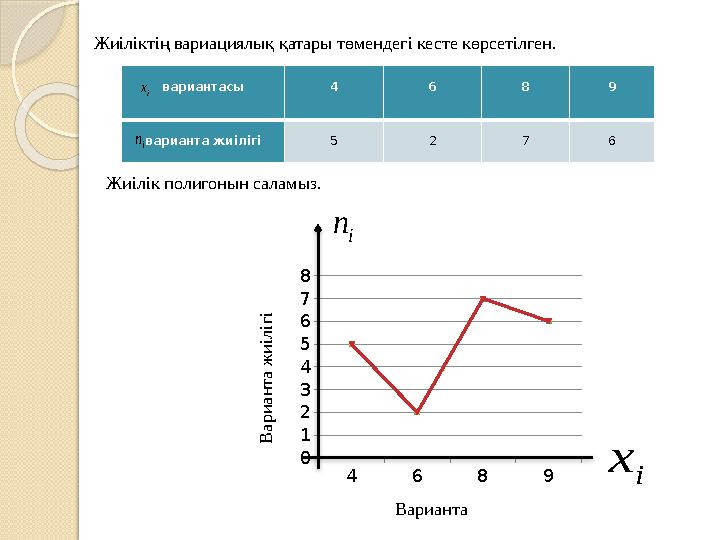
і хЖиілік полигонын саламыз. 4 6 8 9 0 1 2 3 4 5 6 7 8 В арианта ж иілігі i nЖиіліктің вариациялық қатары төмендегі кесте көрсетілген. вариантасы 4 6 8 9 варианта жиілігі 5 2 7 6 іх in Варианта

7 слайд

8 слайд
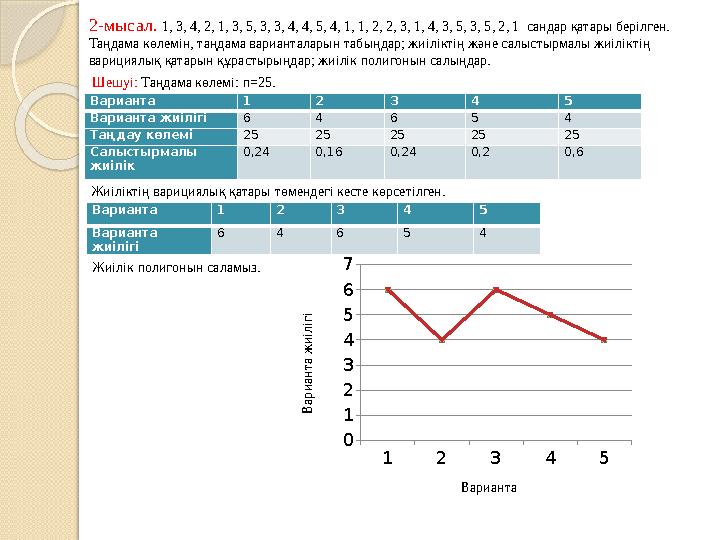
2-мысал. 1, 3, 4, 2, 1, 3, 5, 3, 3, 4, 4, 5, 4, 1, 1, 2, 2, 3, 1, 4, 3, 5, 3, 5, 2, 1 сандар қатары берілген. Таңдама көлемін, таңдама варианталарын табыңдар; жиіліктің және салыстырмалы жиіліктің варициялық қатарын құрастырыңдар; жиілік полигонын салыңдар. Шешуі: Таңдама көлемі: n=25. Варианта 1 2 3 4 5 Варианта жиілігі 6 4 6 5 4 Таңдау көлемі 25 25 25 25 25 Салыстырмалы жиілік 0,24 0,16 0,24 0,2 0,6 Жиіліктің варициялық қатары төмендегі кесте көрсетілген. Варианта 1 2 3 4 5 Варианта жиілігі 6 4 6 5 4 Жиілік полигонын саламыз. 1 2 3 4 5 0 1 2 3 4 5 6 7 Варианта Варианта жиілігі

8 слайд

9 слайд
Өзіндік жұмыс. № 1. 5, 4, 8, 6, 8, 5, 4, 4, 5, 4, 8, 6, 6, 8, 4, 8, 5, 8, 5, 8 сандар қатары берілген. Таңдама көлемін, таңдама варианталарын табыңдар; жиіліктің және салыстырмалы жиіліктің варициялық қатарын құрастырыңдар. № 2. 5, 9, 4, 8, 6, 8, 5, 9, 4, 4, 5, 4, 9, 8, 6, 6, 8, 9, 4, 8, 5, 8, 5, 8, 9 сандар қатары берілген. Таңдама көлемін, таңдама варианталарын табыңдар; жиіліктің және салыстырмалы жиіліктің вариациялық қатары мен салыстырмалы жиіліктің пайызбен берілген қатарын құрастырыңдар. Варианта Варианта жиілігі Таңдау көлемі Салыстырмалы жиілік - бен берілген жиілік00Шешуі: Салыстырмалы жиілікті пайызбен есептегенде салыстырмалы жиіліктің мәнін 100 пайызға көбейтеміз. Варианта Варианта жиілігі Таңдау көлемі Салыстырмалы жиілік

9 слайд

10 слайд
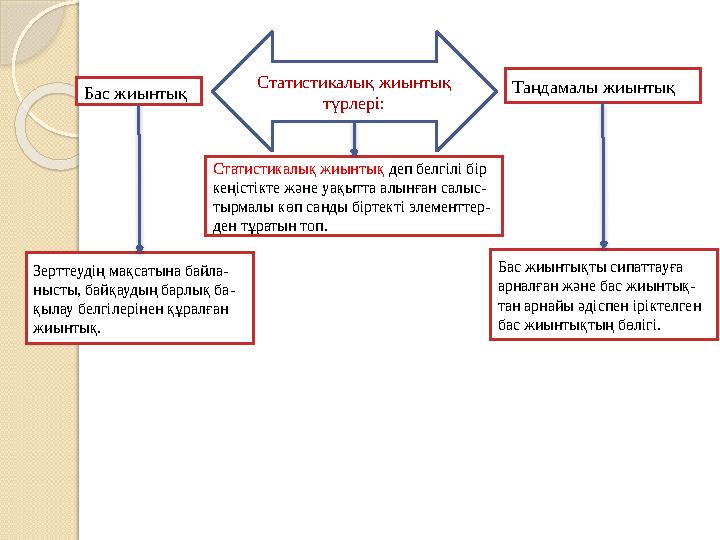
Бас жиынтық Статистикалық жиынтық деп белгілі бір кеңістікте және уақытта алынған салыс- тырмалы көп санды біртекті элементтер- ден тұратын топ. Таңдамалы жиынтық Зерттеудің мақсатына байла- нысты, байқаудың барлық ба- қылау белгілерінен құралған жиынтық. Бас жиынтықты сипаттауға арналған және бас жиынтық- тан арнайы әдіспен іріктелген бас жиынтықтың бөлігі.Статистикалық жиынтық түрлері:

10 слайд

11 слайд
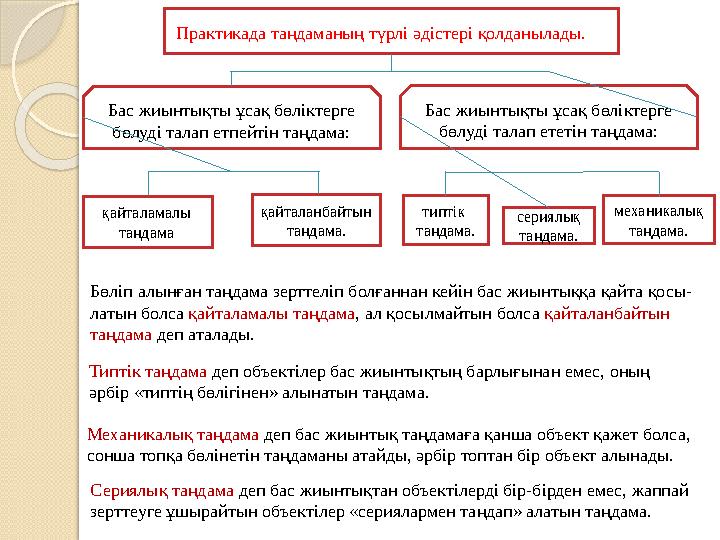
Практикада таңдаманың түрлі әдістері қолданылады. Бас жиынтықты ұсақ бөліктерге бөлуді талап етпейтін таңдама: Бас жиынтықты ұсақ бөліктерге бөлуді талап ететін таңдама: қайталамалы таңдама қайталанбайтын таңдама. механикалық таңдама.типтік таңдама. сериялық таңдама. Бөліп алынған таңдама зерттеліп болғаннан кейін бас жиынтыққа қайта қосы- латын болса қайталамалы таңдама , ал қосылмайтын болса қайталанбайтын таңдама деп аталады. Типтік таңдама деп объектілер бас жиынтықтың барлығынан емес, оның әрбір «типтің бөлігінен» алынатын таңдама. Механикалық таңдама деп бас жиынтық таңдамаға қанша объект қажет болса, сонша топқа бөлінетін таңдаманы атайды, әрбір топтан бір объект алынады. Сериялық таңдама деп бас жиынтықтан объектілерді бір-бірден емес, жаппай зерттеуге ұшырайтын объектілер «сериялармен таңдап» алатын таңдама.

11 слайд

12 слайд
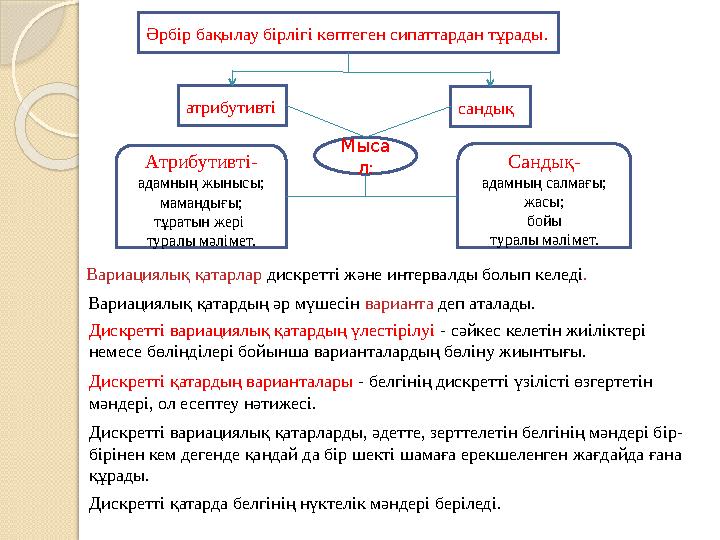
Әрбір бақылау бірлігі көптеген сипаттардан тұрады. атрибутивті сандық Атрибутивті- адамның жынысы; мамандығы; тұратын жері туралы мәлімет. Сандық- адамның салмағы; жасы; бойы туралы мәлімет.Мыса л: Вариациялық қатардың әр мүшесін варианта деп аталады. Вариациялық қатарлар дискретті және интервалды болып келеді . Дискретті вариациялық қатардың үлестірілуі - сәйкес келетін жиіліктері немесе бөлінділері бойынша варианталардың бөліну жиынтығы. Дискретті қатардың варианталары - белгінің дискретті үзілісті өзгертетін мәндері, ол есептеу нәтижесі. Дискретті вариациялық қатарларды, әдетте, зерттелетін белгінің мәндері бір- бірінен кем дегенде қандай да бір шекті шамаға ерекшеленген жағдайда ғана құрады. Дискретті қатарда белгінің нүктелік мәндері беріледі.

12 слайд

13 слайд
3 -мысал. 20 кәсіпорынның тарифтік разряды туралы деректер берілген. 2, 3, 2, 4, 4, 5, 5, 4, 6, 3, 1, 4, 4, 5, 5, 6, 4, 3, 2, 3 тарифтік разрядпен жұмыс- шыларды бөлудің дискретті вариациялық қатарын құрастырыңдар. Шешуі: Кесте екі жолдан тұрады. Бірінші жол – варианта, жұмысшылардың тарифтік разряды; Екінші жол – жиілік, яғни варианталардың кездесу жиілігі, мысалда белгілі бір разряд бойынша жұмысшылар саны. Тапсырманың шартын ескере отырып, кем дегенде бір рет кездесетін мәндерді анықтаймыз. Ол сандар: 1, 2, 3, 4, 5, 6. Содан кейін вариантаның әрбір мәнінің қанша рет кездесетінін санаймыз және кесте толтырамыз. Тарифтік разряд 1 2 3 4 5 6 Жұмысшылар саны 1 3 4 6 4 2іx in Нәтижесінде тарифтік разряд бойынша жұмысшыларды бөлудің дискретті вариациялық қатары алынды.

13 слайд

14 слайд
Вариация – жиынтықтың жеке бірліктерінің белгісі мәнінің аутқуы, әртүрлі- лігі және өзгерілуі . Вариация деп зерттелетін жиынтықтың кез-келген бірлігі белгісі мәнінің бір кезеңдегі және мезеттегі құбылмалылығын айтады. Вариация мәні: - Оның өзгеруі басқа өзгермелі белгілердің сол белгіге әсер ету деңгейін бағалауға мүмкіндік береді. - -ститистикалық модельдерді құруға қолданады. Вариациялық қатардың негізгі белгіленулері: варианта, зерттеліп отырған белгінің сандық өрнектелуі; вариантаның жиілігі, оның вариация қатарда қайталану саны; бақылаудың жалпы саны, таңдама көлемі ( яғни, барлық жиіліктердің қосындысы, айырмасы өлшемнің құлашы немесе ең үлкен және ең кіші вариа - цияның айырмасы ( қатардың құрамы ( яғни, ең жоғарғы ең төменгі варианталардың айырымы ix in n )   in n  min max ,x x  R ) min max x x R  Вариациялық қатарлар – зерттелетін белгінің сандық мөлшерін жоғарлату немесе төмендету ретімен орналастыру.  min max ,x x  maxx ) minx

14 слайд

15 слайд
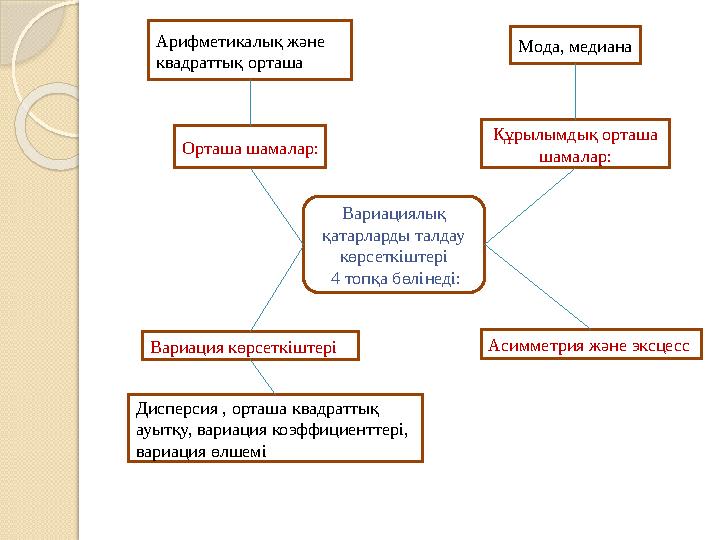
Орташа шамалар: Құрылымдық орташа шамалар: Вариация көрсеткіштері Асимметрия және эксцессВариациялық қатарларды талдау көрсеткіштері 4 топқа бөлінеді:Арифметикалық және квадраттық орташа Мода, медиана Дисперсия , орташа квадраттық ауытқу, вариация коэффициенттері, вариация өлшемі

15 слайд

16 слайд
Вариация өлшемі деп белгінің ауытқушылығын көрсететін абсолюттік және қатысты көрсеткіштерді айтады. Вариация коэффициенті – бұл вариациялық қатардың өзгергіштігінің салыс - тырмалы өлшемі. Вариация коэффициенті (C) –орта квадраттық ауытқудың орта арифметикалық шамаға пайыздық қатынасы тең: Вариациялық ауқымды - белгі мәнінің үлкені және кішісі арасындағы әртүрлілігі Жиынтықтағы варианталарды зерттеу үшін, оларды вариациялық қатарлар ретінде жазады. Вариациялық қатардағы ең көп кездесетін вариантаны мода деп аталады. Вариациялық қатардың ортасында орналасқан варианта медиана деп аталады. Мода , ал медиана белгілерімен белгіленеді.о М е М     100 x С 

16 слайд

17 слайд
варианталар Егер таңдама вариациялық қатармен берілсе, онда х … n …1x 2x kx 1n 2n kn мұндағы: , 1 n x n X k i i i Т     ix in варианталар c алмағы ( жиілігі )    in n таңдамалы көлемі.Арифметикалық таңдамалы орта . Белгінің ( Х ) арифметикалық ортасы деп варианталардың жалпы санына ( таңдаманың көлеміне ) қатынасын айтады, яғни ( егер барлық варианталар әртүрлі болса ) : , 1 n x X k i i Т    мұндағы: варианталар ( белгі мәндері ) таңдаманың көлемі. ix     k i in n 1 ТX

17 слайд

18 слайд
, ,..., , , ,..., , 1 2 1 1 2 1    m m m m x x x x x xонда бұл үйлестіру үшін Медиана mx Егер белгінің өзгеруші мәндері тақ болса, өсу ретімен орналасса 1 m варианта c ы- медианасы ). ( е М ) ( е М ,m е x М  өйткені   m е x М нен төменде жоғары да белгінің саны мәндері орналасқан. на тең, яғни бірдей Варианта саны жұп болса, , ,..., , , ,..., , 2 1 1 2 1 m m m m x x x x x x   онда бұл жиынтықты тең екіге бөлетін медиана мәні аралығында болады. Бұл жағдайда медиана нің мәні осы екі вариантаның арифметикалық ортасы болады, яғни е М 2 1   m m е x x М ) , ( 1m m x x Мода ). ( о М Берілген варициялық қатардың ең жиі кездесетін вариантасын мода дейміз. Басқаша айтқанда, ең жоғары жиілікке сәйкес варианта мәні мода болады. Жиындықты тең етіп екіге бөлетін белгі мәнін медиана деп атаймыз. Вариация құрамы. Ауытқу сипаттамаларының ішіндегі ең қарапайым – вариация құрамы . Мәні R белгінің максимум және минимум мәнінің айырымына тең: min max x x R  

18 слайд

19 слайд
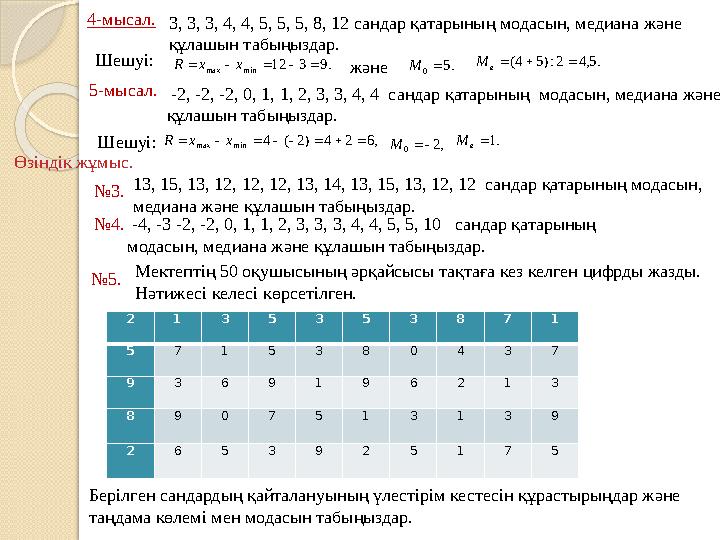
4-мысал. 3, 3, 3, 4, 4, 5, 5, 5, 8, 12 сандар қатарының модасын, медиана және құлашын табыңыздар. Шешуі: .9 3 12 min max      x x R ,2 0   M және .5 0 M .5,4 2:)5 4(   е M 5-мысал. -2, -2, -2, 0, 1, 1, 2, 3, 3, 4, 4 сандар қатарының модасын, медиана және құлашын табыңыздар. Шешуі: ,6 2 4 )2 ( 4 min max         x x R .1е M № 3. 13, 15, 13, 12, 12, 12, 13, 14, 13, 15, 13, 12, 12 сандар қатарының модасын, медиана және құлашын табыңыздар. № 4. -4, -3 -2, -2, 0, 1, 1, 2, 3, 3, 3, 4, 4 , 5, 5, 10 сандар қатарының модасын, медиана және құлашын табыңыздар. № 5. Мектептің 50 оқушысының әрқайсысы тақтаға кез келген цифрды жазды. Нәтижесі келесі көрсетілген. Берілген сандардың қайталануының үлестірім кестесін құрастырыңдар және таңдама көлемі мен модасын табыңыздар. 2 1 3 5 3 5 3 8 7 1 5 7 1 5 3 8 0 4 3 7 9 3 6 9 1 9 6 2 1 3 8 9 0 7 5 1 3 1 3 9 2 6 5 3 9 2 5 1 7 5Өзіндік жұмыс.

19 слайд

20 слайд
Түзілетін дисперсия: Орташа квадраттық ауытқу:ТD n n    1 2  Т Т D       100 T T x V  Вариация коэффициенті:Белгі мәндерінің арифметикалық ортадан ауытқу квадраттары қосындысының арифметикалық ортасын таңдамалы дисперсия деп айтамыз.        n x x n D Т i i Т 2 2         n x x D Т i Т 2 2  немесе өлшенген түрі, жай түрі.Кездейсоқ шамамен оның математикалық күтімі айырымының квадратының математикалық күтімін дисперсия ( шашырау ) дейді. Х кездейсоқ шамасының дисперсиясын арқылы белгілесек, онда анықтама бойынша: ) (x D  2) ( ) ( X M X M x D  Дисперсия ) (x D Ассимметрия: Эксцесс:   3 3      n n x x A i i   4 4      n n x x E i i

20 слайд

21 слайд
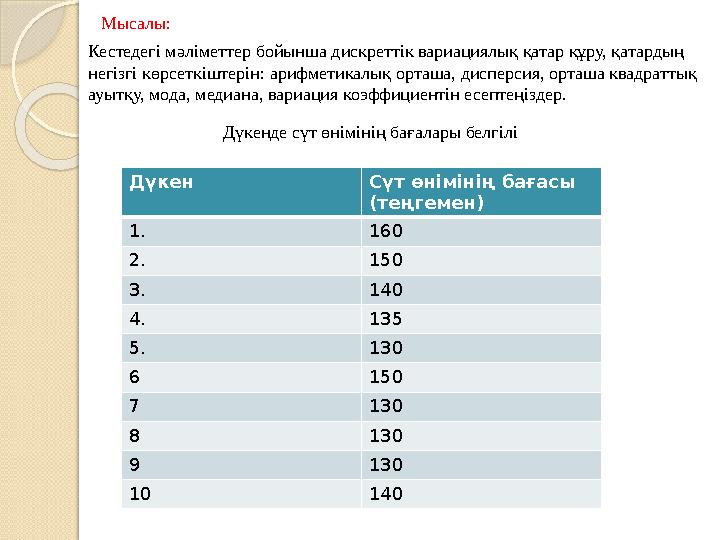
Дүкен Сүт өнімінің бағасы ( теңгемен ) 1. 160 2. 150 3. 140 4. 135 5. 130 6 150 7 130 8 130 9 130 10 140Мысалы: Кестедегі мәліметтер бойынша дискреттік вариациялық қатар құру, қатардың негізгі көрсеткіштерін: арифметикалық орташа, дисперсия, орташа квадраттық ауытқу, мода, медиана, вариация коэ...

21 слайд