Бүкіл әлемдік тартылыс заңы

1 слайд

1 слайд

2 слайд
 Бір бірімізбен сөйлесіп тұрғанда арамыздағы тартылысты неге ? сезбейміз  Адам неге құс сияқты ұшып ? кетпейді

2 слайд

3 слайд
 Заңды .  И Ньютон 1667  .. жылы ашты 1665  жылы 23- жасында Ньютон Айды орбитада ұстап тұратын күш Жерге алманың құлауына септігін тигізетін күш табиғатына . ұқсас екендігін болжап айтты Оның болжамы бойынша Әлемдегі барлық денелер арасында массалар центрін жалғастыратын түзу бойымен тартылыс ( ) . гравитациялық күштер күштері әсер етеді (. 1.10.1 - сурет ).    1.10.1 - сурет . Денелер арасындағы г равитаци ялық күштер 

3 слайд

4 слайд
 Ньютон онан кейінгі жылдары астроном .  И Кеплер дің XVII  ғасыр басында ашқан ғаламшарлардың қозғалыс заңдылығының физикалық түсіндірмесін табуға тырысты және гравитациялық күштердің сан мәні қанша болатынын . есептеді Ғаламшарлардың қалай қозғалатынын біле отырып Ньютон оларға қандай күштер әсер ететіндігін анықтағысы келді . Бұл әдіс механиканың кері есебі механиканың кері есебі . деп аталады

4 слайд

5 слайд
Механиканың негізгі есебі бойынша массасы мен жылдамдығы белгілі денеге әсер ететін күштің салдарынан кез келген уақыт мезетіндегі дененің орнын анықтау болса , механиканың кері есебінде дененің қалай қозғалатындығына қарай оған әсер ететін күштерді анықтау болып табылады

5 слайд

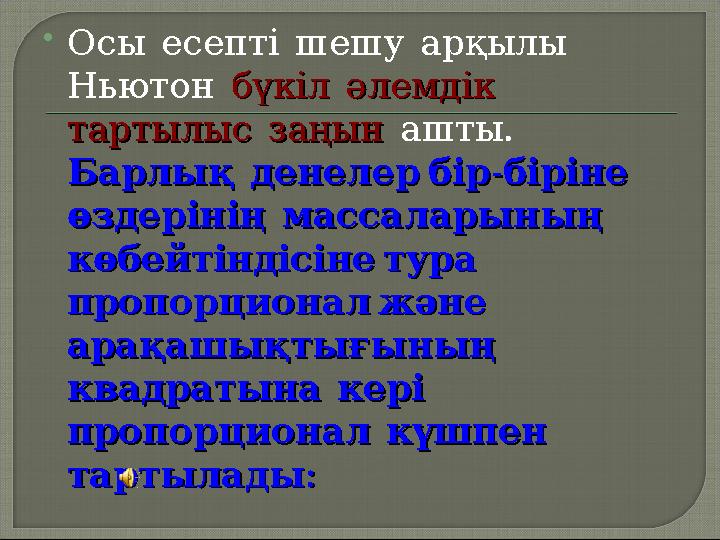
6 слайд
 Осы есепті шешу арқылы Ньютон бүкіл әлемдік бүкіл әлемдік тартылыс заңын тартылыс заңын ашты . - Барлық денелер бір біріне - Барлық денелер бір біріне өздерінің массаларының өздерінің массаларының көбейтіндісіне тура көбейтіндісіне тура пропорционал және пропорционал және арақашықтығының арақашықтығының квадратына кері квадратына кері пропорционал күшпен пропорционал күшпен : тартылады:тартылады

6 слайд

7 слайд
П ропорционал дық коэфициент G табиғаттағы барлық денелер үшін бірдей және оны бүкіл бүкіл әлемдік тартылыс тұрақтысы әлемдік тартылыс тұрақтысы немесе гравитациялық тұрақты гравитациялық тұрақты . деп атайды  G  = 6,67·10 -11   · Н м 2 / 2 ( ). кг СИ

7 слайд

8 слайд
Табиғаттағы көптеген құбылыстар Табиғаттағы көптеген құбылыстар . бүкіләлемдік тартылыс күшімен түсіндіріледі .бүкіләлемдік тартылыс күшімен түсіндіріледі  1 . , Күн жүйесіндегі ғаламшарлар қозғалысы  2. , жердің жасанды серігінің қозғалыстары  3. баллистикалық зымырандардың ұшу траекториясы  4. , Жерге жақын денелердің қозғалысы  5. , Денелердің жерге құлауы  6. , Тасу және қайту  7. , Сарқырамалар  8. . Қол сөмкесінің ауырлығы  9. . Жер атмосферасының болуы т б құбылыстар  динамика заңдарымен және бүкіләлемдік тартылыс заңы арқылы түсіндіріледі

8 слайд

9 слайд
 Е гер M – Жер масса сы , R – З оның радиус ы , m – берілген дене масса сы болса , онда ауырлық күші  мұндағы g – Жер бетіндегі еркін . түсу үдеуі : Бүкіләлемдік тартылыс заңының бір байқалуыБүкіләлемдік тартылыс заңының бір байқалуы ауырлық күші болып табылады.ауырлық күші болып табылады.  Жер бетіне жақын денелердің тарту күшін Жер бетіне жақын денелердің тарту күшін  осылай атау қабылданғаносылай атау қабылданған

9 слайд

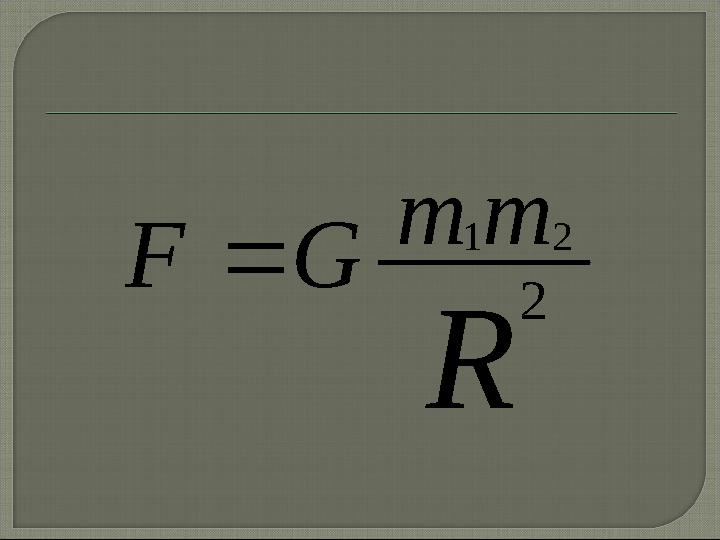
10 слайд
R m m G F 2 2 1 

10 слайд

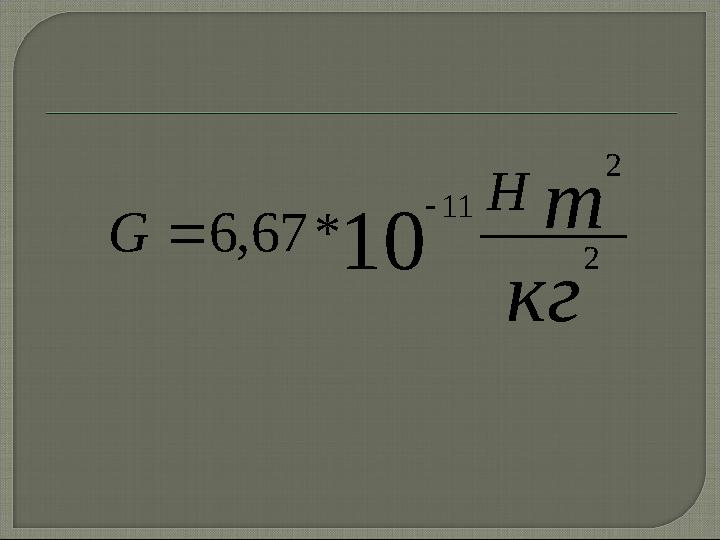
11 слайд
кг m H G 2 2 11 10 * 67 , 6  

11 слайд

12 слайд
 Ауырлық күші жер центріне қарай бағытталған . Басқа күштер болмағанда дене Жерге еркін түсу үдеуімен . құлайды Жердің әр түрлі нүктелеріндегі еркін түсу үдеуінің орташа мәні 9,81  / м с 2 . Жердің радиусы мен еркін түсу үдеуінің мәнін біле отырып ( R з  = 6,38·106  ), м Жер массасын . М есептеп шығаруға болады :

12 слайд

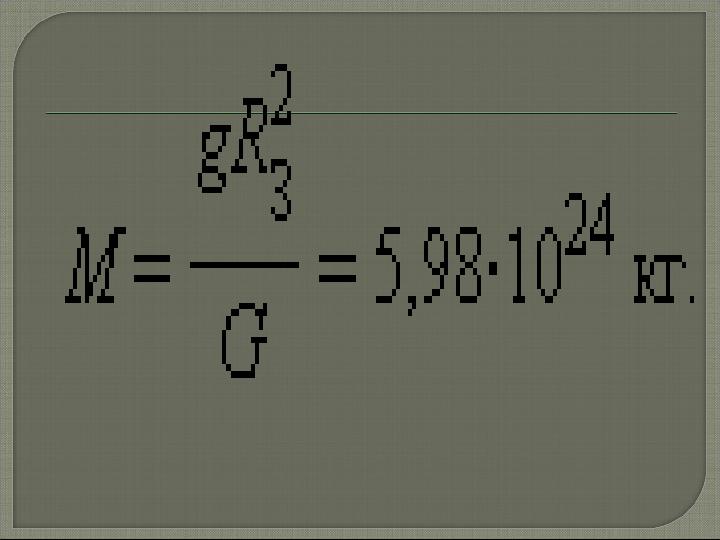
13 слайд

13 слайд

14 слайд
 Жерден қашықтаған сайын Жердің тарту күші мен еркін түсу үдеуі Жер центріне дейінгі ара қашықтықтың квадратына кері пропорционал . өзгереді  1.10.2 - сурет Жерден қашықтап бара жатырған ғарыш кемесінің ішіндегі ғарышкерге әсер ететін тартылыс . күшінің өзгеруі бейнеленген Жерге жақын маңда ғарышкерге әсер ететін тарту күші 700  Н - : ғатең деп алсақ

14 слайд

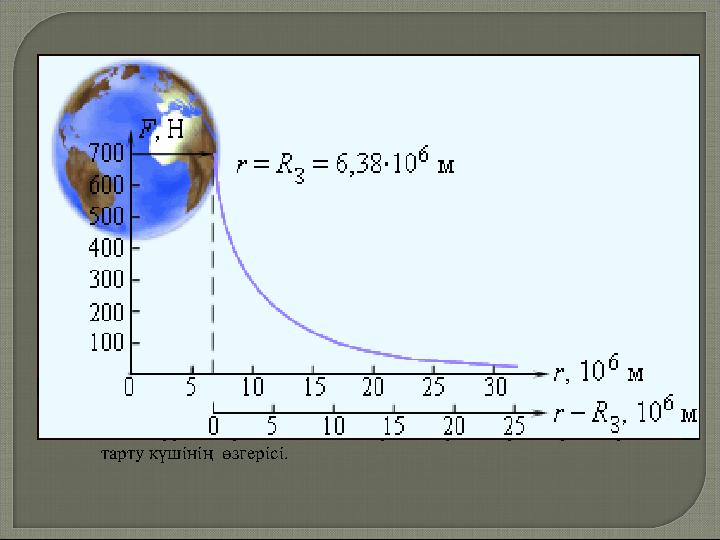
15 слайд
 1.10.2 -сурет . Жерден қашықтап бара жатырған ғарышкерге әсер ететін тарту күшінің өзгерісі.

15 слайд

16 слайд
Өзара әсерлесетін денелерге Жермен Айды алуға болады.Ай мен Жердің арасы r  = 3,84·106 м. Бұл қашықтық Жер радиусынан 60  есе артық..

16 слайд

17 слайд
 Жердің тартуы салдарынан Ай орбитасындағы еркін түсу үдеуі  . Ай осындай үдеумен Жер центріне бағыттала отырып . қозғалады Сондықтан мұндай үдеуді центрге тартқыш үдеу центрге тартқыш үдеу . деп аталады Оны төмендегі центрге тартқыш үдеудің кинематикалық формуласымен есептейді :

17 слайд

18 слайд
 Мұндағы T  = 27,3  с ө т ке – Айдың Жерді айналу . периоды Әр түрлі әдістер арқылы есептеулер нәтижелерінің дәл келуі Ньютонның Айды , орбитада устап тұрған күшпен ауырлық күшінің табиғатының ұқсас деген болжамын . дәлелдейді . Айдың массасын Жер 81 , массасынан есе жеңілдеп радиусы Жер 3,7 радиусынан есе аз деп есептеп Ай бетіндегі еркін түсу үдеуін g л – мына формуламен : есептейміз

18 слайд

19 слайд
Мұндай әлсіз тартылысты Айға қонған ғарышкерлер бастан кешті.Адамдар дәл осындай жағдайда өте үлкен биіктікке оңай секіре алады.Жер бетінде адам 1 метр биіктікке секіреді деп есептесек Айда ол адам 6 м биіктікке секіре алады.

19 слайд