Бұрыштық және сызықтық жылдамдықтар

#1 слайд

1 слайд

#2 слайд
• Бұрыштық жылдамдық  — қатты дененің айналу шапшаңдығын сипаттайтын векторлық шама; дененің айналмалы қозғалысының кинематика лық мөлшері, ω  модулі өте аз уақыт ішінде айналу бұрышының сол уақытқа қатынасымен, ал бағыты айналу осінің бойымен дененің айналуы сағат тілінің бағытына қарсы бағытта көрінетін бағытымен бағыттас вектор.

2 слайд

#3 слайд
Бұрыштық жылдамдық деп дененің бұрылу бұрышының осы бұрылуға кеткен уақытқа қатынасымен өлшенетін шаманы ай тады. Бұрылу бұрышы  φ  әрпімен белгіленеді.t t t d d lim 0            

3 слайд

#4 слайд
, lim lim 0 0   R t R t S V t t           • Дененің шеңбер бойымен қозғалысын қарастырғанда, дененің түзусызықты қозғалысын сипаттайтын жылдамдық та колданыла береді. Бірақ дененің шеңбер бойымен қозғалысыжағдайында оны сызықтық жылдамдық деп атау келісілген. • Шеңбер бойымен қозғалыс кезінде сызықтық жылдамдықтың бағыты шеңбердің жанамасымен бағытталады.

4 слайд

#5 слайд
R R R R a n 2 2 2 2      S=R φ υ =R ω a τ =R ε a n = ω 2 R• Алдыңғы сабақтарда ш еңберді айналу барысында дененің жылдамдық векторының бағыты тұрақты өзгеріп отыруна байланысты үдеуді тудыранын айтылған. • Лездік жылдамдықты шеңбер радиусының уақытқа қатынасы деп алсақ: • Шеңбер бойымен айналатын қозғалыстың барлық сипаттамаларының бір- біріне қатынасын табамыз. , d υ d υ lim a 0 t t t         

5 слайд

#6 слайд
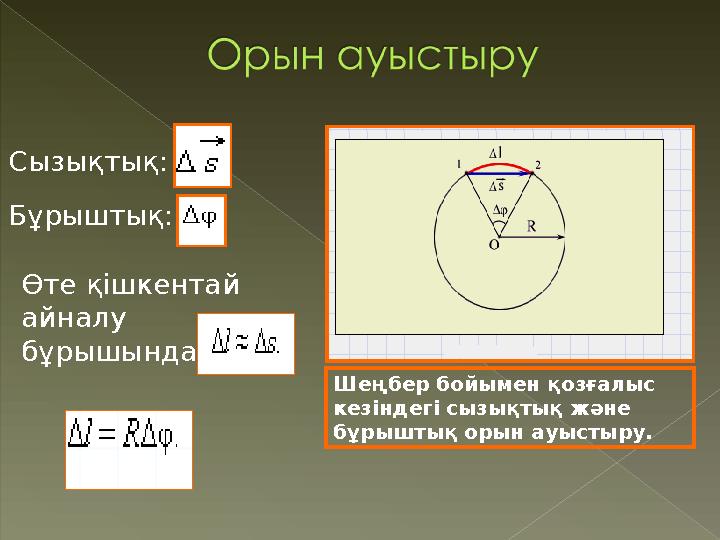
Сызықтық: Бұрыштық: Өте қішкентай айналу бұрышында: Шеңбер бойымен қозғалыс кезіндегі сызықтық және бұрыштық орын ауыстыру.

6 слайд

#7 слайд
   2 Бір айналым үшін рад  ] [  Радиан - араларындағы доғасының ұзындығы осы шеңбердің радиусына тең, шеңбердің екі радиусының арасындағы бұрышқа тең СИ жүйесіндегі жазық бұрыштың бірлігі. Өлшем бірлігі:

7 слайд

#8 слайд
Айналу периоды (Т) деп н үктенің шеңбер бойымен бір айналым жасауға кеткен уақытын айтады.   с Т 1  t – айналым уақыты; N – айналым саны. N t Т 

8 слайд

#9 слайд
Жер шарында бір жылда 365 күн бар екені белгілі және де осы 365 күн Жердің Күнді айналу периоды болып табылады.

9 слайд

#10 слайд
Айналым жиілігі – дененің бірқалыпты шеңбер бойымен қозғалысы кезінде бір секунд ішінде дененің айналып шыққын айналым саны . Т 1     Гц с с об 1 1 / 1 1     

10 слайд

#11 слайд
Айналу периоды – н үктенің шеңбер бойымен бір айналым жасауға кеткен уақытын айтады . Айналым жиілігі – бір секунд ішінде дененің айналып шыққын айналым саны . Т = nt v = tn Т = v1Айналу периоды мен жиілігінің қатынасы: v = T1[ Т ] = c [ v ] = 1 /c

11 слайд

#12 слайд
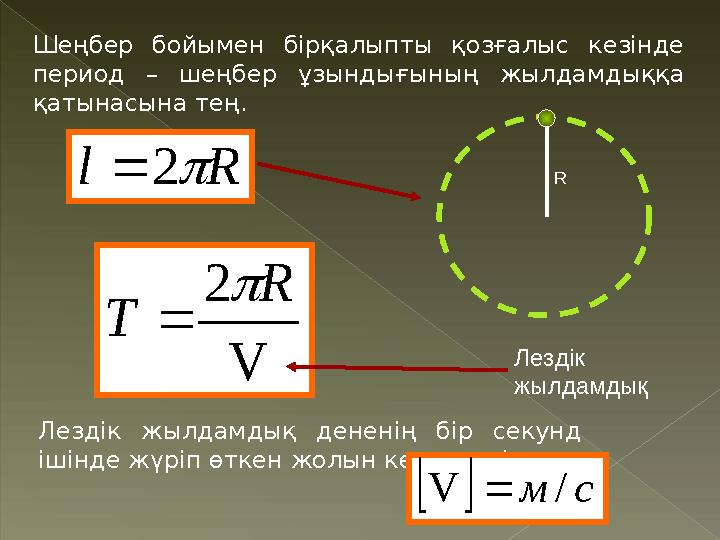
Шеңбер бойымен бірқалыпты қозғалыс кезінде период – шеңбер ұзындығының жылдамдыққа қатынасына тең. V 2 R T   R l  2  Лездік жылдамдық Лездік жылдамдық дененің бір секунд ішінде жүріп өткен жолын көрсетеді.   c м / V  R

12 слайд

#13 слайд
Егер де шеңбер бойымен бірқалыпты қозғалыс кезінде ( ω = const ) дене бір айналым жасап шықса , онда айналым уақыты периодқа Т, ал бұрыштық орын ауыстыру Δ φ = 2 π те ң. екені белгілі болса, ω =2 π /T Олай болса, Айналу жиілігі тең екендігі белгілі болса, онда: ω =2 π vt t t d d lim 0                2 T   2 / 1   T v

13 слайд