Материалдар / Cлайд "Интегралдың көмегімен фигуралардың аудандарын есептеу

Cлайд "Интегралдың көмегімен фигуралардың аудандарын есептеу

Материал туралы қысқаша түсінік

оқушыларға

Кашанбаева Клара Сарсенбаевна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

17 Сәуір 2020

377

0 рет жүктелген

Алгебра Презентация 11 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 8

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
«М. ТЫНЫШПАЕВ АТЫНДАҒЫ ҚАЗАҚ КӨЛІК ЖӘНЕ КОММУНИКАЦИЯЛАР АКАДЕМИЯСЫ» АҚ «АҚТӨБЕ КОЛЛЕДЖІ» ЖШС САБАҚ ТАҚЫРЫБЫ: А НЫҚТАЛҒАН ИНТЕГРАЛ ЖӘНЕ ОНЫҢ ҚАСИЕТТЕРІ ПӘН : МАТЕМАТИКА КУРС: 1 курс ОҚЫТУШЫ : КАШАНБАЕВА К.С.

1 слайд

«М. ТЫНЫШПАЕВ АТЫНДАҒЫ ҚАЗАҚ КӨЛІК ЖӘНЕ КОММУНИКАЦИЯЛАР АКАДЕМИЯСЫ» АҚ «АҚТӨБЕ КОЛЛЕДЖІ» ЖШС САБАҚ ТАҚЫРЫБЫ: А НЫҚТАЛҒАН ИНТЕГРАЛ ЖӘНЕ ОНЫҢ ҚАСИЕТТЕРІ ПӘН : МАТЕМАТИКА КУРС: 1 курс ОҚЫТУШЫ : КАШАНБАЕВА К.С.

2 слайд
Анықталған интеграл: • белгіленуі : • оқылуы: икстен эф дэ икстің а-дан b- ге дейінгі интегралы. • а және b сандары интегралдау шектері: а - төменгі шегі, ал b –жоғарғы шегі.

2 слайд

Анықталған интеграл: • белгіленуі : • оқылуы: икстен эф дэ икстің а-дан b- ге дейінгі интегралы. • а және b сандары интегралдау шектері: а - төменгі шегі, ал b –жоғарғы шегі.

3 слайд
Аны қталған интегралдың негізгі қасиеттері: • 1. • 2. • 3. • 4. = - • 5.

3 слайд

Аны қталған интегралдың негізгі қасиеттері: • 1. • 2. • 3. • 4. = - • 5.

4 слайд
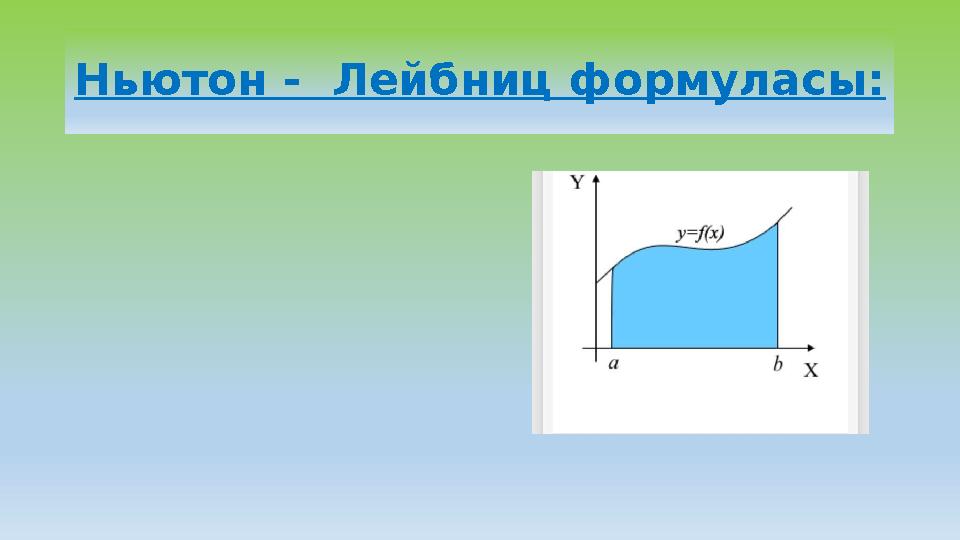
Ньютон - Лейбниц формуласы:

4 слайд

Ньютон - Лейбниц формуласы:

5 слайд
Исаак Ньютон, ағылш. Sir Isaac Newton ( 4 қаңтар 1643 жыл — 31 наурыз 1727) — ағылшын физигі , математигі , астрономы , табиғи философы , алхимигі және теологы , Корольдік қоғамның мүшесі . Готфрид Вильгельм Лейбниц, ( нем. Gottfried Wilhelm Leibniz (1646-1716) - неміс философы және ғалымы , жаңа заман философиясының рационолистік дәстүрінің жалғастырушысы.

5 слайд

Исаак Ньютон, ағылш. Sir Isaac Newton ( 4 қаңтар 1643 жыл — 31 наурыз 1727) — ағылшын физигі , математигі , астрономы , табиғи философы , алхимигі және теологы , Корольдік қоғамның мүшесі . Готфрид Вильгельм Лейбниц, ( нем. Gottfried Wilhelm Leibniz (1646-1716) - неміс философы және ғалымы , жаңа заман философиясының рационолистік дәстүрінің жалғастырушысы.

6 слайд
Мысал: 1 - есеп : | = = + = = 3 2 - есеп: = -(-1)+1=1+1 = 2

6 слайд

Мысал: 1 - есеп : | = = + = = 3 2 - есеп: = -(-1)+1=1+1 = 2

7 слайд
Тапсырмалар :

7 слайд

Тапсырмалар :