Доклад "Математическая статистика в медицине"

1 слайд
«Математическая статистика в медицине»КГУ «Средняя общеобразовательная школа №32» Учителя математики: Аягузова Жанара Ержурековна Шайкакова Гульнар Сейткалиевна 2019год, г.Семей

1 слайд

2 слайд
"Математика - основа всего точного естествознания" Давид Гильберт Введение Здоровье человека относится к глобальным проблемам, решение которых зависит от усилий отдельных профессиональных групп, к которым относятся работники медицины. Использование математики в такой области как медицина, имеет глубоко уходящие в историю корни. Вместе с тем ввиду развития научно- технического прогресса процесс укрепления взаимосвязи между математикой и данной сферой жизнедеятельности не только не ослабевает, но усиливается еще больше на фоне всеобщей информатизации. Все глубже и глубже изучая математику, наблюдая за процессом изменений и развития в области медицины, мы можем предположить между ними тесную взаимосвязь. Математика и медицина часто требуют одних и тех же приемов: прежде всего - это наблюдения, анализ, диагностика, неоднократная проверка полученных результатов. Внимание, терпение и настойчивость - вот качества, необходимые врачу и математику.

2 слайд

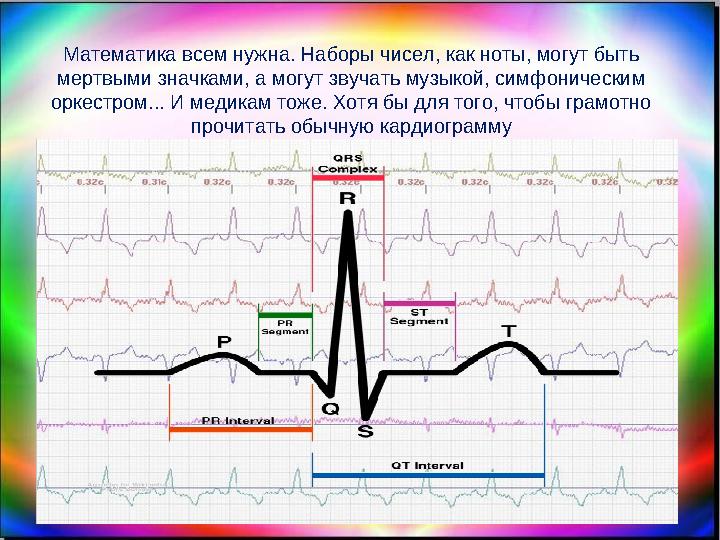
3 слайд
Математика всем нужна. Наборы чисел, как ноты, могут быть мертвыми значками, а могут звучать музыкой, симфоническим оркестром... И медикам тоже. Хотя бы для того, чтобы грамотно прочитать обычную кардиограмму

3 слайд

4 слайд
Без знания азов математики трудно разобраться в компьютерной технике, использовать возможности компьютерной томографии... Ведь современная медицина не может обходиться без сложнейшей техники.

4 слайд

5 слайд
Без знания математики невозможно не только сделать лечебные и диагностические приборы и оборудование, но и работать на них.

5 слайд

6 слайд
Такая важная отрасль медицины, как хирургия также не может обойтись без математики. Для лапароскопических (безкровных) операций нужна новейшая техника.

6 слайд

7 слайд
И особенно микрохирургия глаза. Ведь погрешность всего лишь в пару миллиметров в операции на глаза может стоить человеку зрения…

7 слайд

8 слайд
Математика и кибернетика — закономерное следствие развития научно-технической революции.

8 слайд

9 слайд
Задача1: Определите концентрацию раствора, полученного при слиянии 150 г 30 % и 250 г 10 % растворов какой-либо соли.

9 слайд

10 слайд
150 г 30% 250 г 10 %II способ. Алгебраический. Масса растворенного вещества в смеси будет слагаться из масс растворенного вещества в исходных растворах, поэтому для удобства решения, данные запишем в виде схемы: + =

10 слайд

11 слайд

11 слайд

12 слайд
Задача №2 : Ребёнок родился ростом 53см. какой рост должен быть у него в 5 месяцев, 3года ? Решение : прирост за каждый месяц жизни составляет: в 1-ой четверти (1-3 месяца) по3 см на каждый месяц, Во 2-ой четверти (4-6 мес.) – 2,5 см, в 3-ей четверти (7-9 мес.) – 1,5 см, в 4-ой четверти (10-12 мес.) – 1,0 см. Рост ребёнка после года можно вычислить по формуле 75+6n Где 75 – средний рост ребёнка в 1 год, 6 – среднегодовая прибавка, n – возраст ребёнка. Ответ: рост ребёнка в 5 месяцев : Х = 53+3 * 3+2 *2,5 = 67см Рост ребёнка в 3 года Х = 75+(6*3) = 93 см

12 слайд

13 слайд

13 слайд

14 слайд
Максимально допустимый пульс - частота пульса, которая соответствует той работе сердца, при которой достигается максимально возможное потребление кислорода работающими мышцами. Существует известная упрощенная математическая формула: МП = 220 – В , где МП – максимальный пульс, В – возраст. Возраст Максимально допустимый пульс (МП) 15 лет 220-15=205 16 лет 220-16=204

14 слайд

15 слайд
Наблюдения за весом Следить за весом тела так же необходимо, как следить за пульсом или артериальным давлением. Излишний вес тела является одним из признаков возможного наличия сердечнососудистых заболеваний. Для изучения весамы использовали индекс Брока. НВ = Р – 100  (до 165 см роста); НВ = Р – 105  (от 165-175 см роста); НВ = Р – 110  (при росте выше 175 см), где НВ – нормальный вес тела; Р – рост.

15 слайд

16 слайд
Расчёт субмаксимального пульса Субмаксимальный пульс рассчитывается как 75% или 85% от максимального. СП = 0,75 х МП  (для людей, имеющих проблемы с сердцем), СП = 0,85 х МП  (для людей тренированных и практически здоровых). Максимально допустимый пульс Субмаксимальный пульс (СП) 15 лет 205 0,75х205=154 16 лет 204 0,85х204=173 Таким образом, максимальный эффект для здоровья мы получаем при нагрузке, соответствующей субмаксимальному пульсу.

16 слайд

17 слайд
Вывод В медицине без математики шагу не ступить.  Проектирование медицинских приборов. Анализ данных об эффективности того или иного лечения. Учёт дозы медицинских препаратов и периодичности приёма лекарств. Периодический и статистический учёт разных, связанных между собой факторов, таких как: возраст, физические параметры тела и т.д. Клинические анализы, где требуется перевод одних единиц в другие. Различная медицинская статистика (например, заболеваемости в зависимости от различных факторов). Всё это требует точного математического расчёта. Профессиональная направленность математической подготовки обеспечивает повышение уровня математической компетентности обучающихся, осознание ценности математики для будущей профессиональной деятельности, развитие профессионально значимых качеств и приёмов умственной деятельности, позволяющего моделировать, анализировать и решать элементарные математические профессионально значимые задачи, имеющие место в медицинской науке и практике, обеспечивая преемственность формирования математической культуры и воспитание потребности в совершенствовании знаний в области математики и её приложений.

17 слайд

18 слайд

18 слайд